2.2 30°,45°,60° 角的三角比 学案(无答案)2024-2025学年青岛版九年级上册
文档属性
| 名称 | 2.2 30°,45°,60° 角的三角比 学案(无答案)2024-2025学年青岛版九年级上册 | 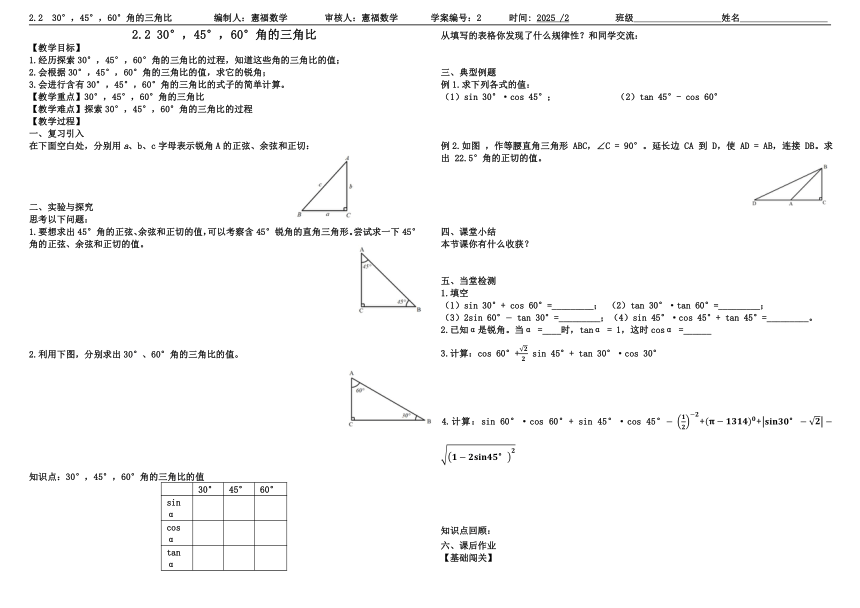 | |
| 格式 | docx | ||
| 文件大小 | 90.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-15 10:53:09 | ||
图片预览

文档简介
2.2 30°,45°,60°角的三角比 编制人:憲福数学 审核人:憲福数学 学案编号:2 时间: 2025 /2 班级 姓名
2.2 30°,45°,60°角的三角比
【教学目标】
1.经历探索30°,45°,60°角的三角比的过程,知道这些角的三角比的值;
2.会根据30°,45°,60°角的三角比的值,求它的锐角;
3.会进行含有30°,45°,60°角的三角比的式子的简单计算。
【教学重点】30°,45°,60°角的三角比
【教学难点】探索30°,45°,60°角的三角比的过程
【教学过程】
一、复习引入
在下面空白处,分别用a、b、c字母表示锐角A的正弦、余弦和正切:
二、实验与探究
思考以下问题:
1.要想求出45°角的正弦、余弦和正切的值,可以考察含45°锐角的直角三角形。尝试求一下45°角的正弦、余弦和正切的值。
2.利用下图,分别求出30°、60°角的三角比的值。
知识点:30°,45°,60°角的三角比的值
30° 45° 60°
sinα
cosα
tanα
从填写的表格你发现了什么规律性?和同学交流:
三、典型例题
例1.求下列各式的值:
(1)sin 30°·cos 45°; (2)tan 45°- cos 60°
例2.如图 ,作等腰直角三角形 ABC,∠C = 90°。延长边 CA 到 D,使 AD = AB,连接 DB。求出 22.5°角的正切的值。
四、课堂小结
本节课你有什么收获?
五、当堂检测
1.填空
(1)sin 30°+ cos 60°=_________; (2)tan 30°·tan 60°=_________;
(3)2sin 60° tan 30°=_________;(4)sin 45°·cos 45°+ tan 45°=_________。
2.已知α是锐角。当α =____时,tanα = 1,这时cosα =______
3.计算:cos 60°+ sin 45°+ tan 30°·cos 30°
4.计算:sin 60°·cos 60°+ sin 45°·cos 45°++
知识点回顾:
六、课后作业
【基础闯关】
1.2cos60°=( )A.1 B. C. D.
2.计算sin245°+cos30° tan60°,其结果是( )
A.2 B.1 C. D.
3.点M(﹣sin60°,cos60°)关于x轴对称的点的坐标是( )
A.() B.() C.() D.()
4.如果△ABC中,sinA=cosB,则下列最确切的结论是( )
A.△ABC是直角三角形 B.△ABC是等腰三角形
C.△ABC是等腰直角三角形 D.△ABC是锐角三角形
5.已知α、β均为锐角,且满足|sinα|0,则α+β=( )
A.60° B.75° C.90° D.105°
6.在Rt△ABC中,∠C=90°,a=1,c,则∠A的度数为( )
A.30° B.45° C.50° D.60°
7.下列式子中正确的有( )个.
①cos40°=sin50° ②tan15° tan75°=1 ③sin22.5°+cos22.5°=1 ④sin60°=2sin30°.
A.1 B.2 C.3 D.4
8.在Rt△ABC中,cosA,那么sinA的值是___________
9.已知α为锐角,且2sin(α﹣10°),则α等于___________.
10.将矩形ABCD沿AE折叠,已知sin∠CEB'=,则∠AEB'的度数为___________.
11.在△ABC中,∠C=90°,tan(A﹣15°),则cosB的值为___________.
12.已知α为锐角,当无意义时,tan(α+15°)﹣tan(α﹣15°)的值是___________.
13.计算:
(1)tan30°﹣cos60°+cos45°;(2)sin45°﹣(tan60°)﹣1+()0+cos230°.
(3) (4).
【能力提升】
14.按如图所示的运算程序,能使输出y值为的是( )
A.α=60°,β=45° B.α=30°,β=45°
C.α=30°,β=30° D.α=45°,β=30°
15.在△ABC中,∠A和∠B都是锐角,且sinA,cosB,则三个内角的大小关系为( )
A.∠C>∠A>∠B B.∠B>∠C>∠A C.∠A>∠B>∠C D.∠C>∠B>∠A
16. 已知α是锐角,当α =___________时,cosα =,这时 tanα=___________
17.在△ABC中,若∠A+∠C=150°,则sinB的值为___________
18.在Rt△ABC中,∠C=90°,∠B=60°,那么sinA+cosB的值为___________
19.在Rt△ABC中,∠C=90°,AB=2,BC,则sin___________.
20.定义一种运算:
sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ.例如:当α=45°,β=30°时,sin(45°+30°),则sin15°的值为___________.
21.已知α是锐角,sin(α+15°),计算4cosα﹣(π﹣3.14)0+tanα+()﹣1
22. 在 Rt△ABC 中,∠C = 90°,a = ,b = ,求∠A,∠B 的度数
【培优创新】
23.利用例2的方法,构造一个图形,然后利用这个图形求 15°及75°角的正切的值。
24.(1)计算:(只要求填写最后结果)sin230°+cos230°=________;sin245°+cos245°=________;sin260°+cos260°=________;…观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A=________.
(2)如图,在锐角三角形ABC中,利用三角函数的定义及勾股定理对∠A证明你的猜想;
(3)已知0°<∠A<90°且sinA cosA,求sinA+cosA的值.
2.2 30°,45°,60°角的三角比
【教学目标】
1.经历探索30°,45°,60°角的三角比的过程,知道这些角的三角比的值;
2.会根据30°,45°,60°角的三角比的值,求它的锐角;
3.会进行含有30°,45°,60°角的三角比的式子的简单计算。
【教学重点】30°,45°,60°角的三角比
【教学难点】探索30°,45°,60°角的三角比的过程
【教学过程】
一、复习引入
在下面空白处,分别用a、b、c字母表示锐角A的正弦、余弦和正切:
二、实验与探究
思考以下问题:
1.要想求出45°角的正弦、余弦和正切的值,可以考察含45°锐角的直角三角形。尝试求一下45°角的正弦、余弦和正切的值。
2.利用下图,分别求出30°、60°角的三角比的值。
知识点:30°,45°,60°角的三角比的值
30° 45° 60°
sinα
cosα
tanα
从填写的表格你发现了什么规律性?和同学交流:
三、典型例题
例1.求下列各式的值:
(1)sin 30°·cos 45°; (2)tan 45°- cos 60°
例2.如图 ,作等腰直角三角形 ABC,∠C = 90°。延长边 CA 到 D,使 AD = AB,连接 DB。求出 22.5°角的正切的值。
四、课堂小结
本节课你有什么收获?
五、当堂检测
1.填空
(1)sin 30°+ cos 60°=_________; (2)tan 30°·tan 60°=_________;
(3)2sin 60° tan 30°=_________;(4)sin 45°·cos 45°+ tan 45°=_________。
2.已知α是锐角。当α =____时,tanα = 1,这时cosα =______
3.计算:cos 60°+ sin 45°+ tan 30°·cos 30°
4.计算:sin 60°·cos 60°+ sin 45°·cos 45°++
知识点回顾:
六、课后作业
【基础闯关】
1.2cos60°=( )A.1 B. C. D.
2.计算sin245°+cos30° tan60°,其结果是( )
A.2 B.1 C. D.
3.点M(﹣sin60°,cos60°)关于x轴对称的点的坐标是( )
A.() B.() C.() D.()
4.如果△ABC中,sinA=cosB,则下列最确切的结论是( )
A.△ABC是直角三角形 B.△ABC是等腰三角形
C.△ABC是等腰直角三角形 D.△ABC是锐角三角形
5.已知α、β均为锐角,且满足|sinα|0,则α+β=( )
A.60° B.75° C.90° D.105°
6.在Rt△ABC中,∠C=90°,a=1,c,则∠A的度数为( )
A.30° B.45° C.50° D.60°
7.下列式子中正确的有( )个.
①cos40°=sin50° ②tan15° tan75°=1 ③sin22.5°+cos22.5°=1 ④sin60°=2sin30°.
A.1 B.2 C.3 D.4
8.在Rt△ABC中,cosA,那么sinA的值是___________
9.已知α为锐角,且2sin(α﹣10°),则α等于___________.
10.将矩形ABCD沿AE折叠,已知sin∠CEB'=,则∠AEB'的度数为___________.
11.在△ABC中,∠C=90°,tan(A﹣15°),则cosB的值为___________.
12.已知α为锐角,当无意义时,tan(α+15°)﹣tan(α﹣15°)的值是___________.
13.计算:
(1)tan30°﹣cos60°+cos45°;(2)sin45°﹣(tan60°)﹣1+()0+cos230°.
(3) (4).
【能力提升】
14.按如图所示的运算程序,能使输出y值为的是( )
A.α=60°,β=45° B.α=30°,β=45°
C.α=30°,β=30° D.α=45°,β=30°
15.在△ABC中,∠A和∠B都是锐角,且sinA,cosB,则三个内角的大小关系为( )
A.∠C>∠A>∠B B.∠B>∠C>∠A C.∠A>∠B>∠C D.∠C>∠B>∠A
16. 已知α是锐角,当α =___________时,cosα =,这时 tanα=___________
17.在△ABC中,若∠A+∠C=150°,则sinB的值为___________
18.在Rt△ABC中,∠C=90°,∠B=60°,那么sinA+cosB的值为___________
19.在Rt△ABC中,∠C=90°,AB=2,BC,则sin___________.
20.定义一种运算:
sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ.例如:当α=45°,β=30°时,sin(45°+30°),则sin15°的值为___________.
21.已知α是锐角,sin(α+15°),计算4cosα﹣(π﹣3.14)0+tanα+()﹣1
22. 在 Rt△ABC 中,∠C = 90°,a = ,b = ,求∠A,∠B 的度数
【培优创新】
23.利用例2的方法,构造一个图形,然后利用这个图形求 15°及75°角的正切的值。
24.(1)计算:(只要求填写最后结果)sin230°+cos230°=________;sin245°+cos245°=________;sin260°+cos260°=________;…观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A=________.
(2)如图,在锐角三角形ABC中,利用三角函数的定义及勾股定理对∠A证明你的猜想;
(3)已知0°<∠A<90°且sinA cosA,求sinA+cosA的值.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
