2.5 解直角三角形的应用复习 学案(无答案)2024-2025学年青岛版九年级上册
文档属性
| 名称 | 2.5 解直角三角形的应用复习 学案(无答案)2024-2025学年青岛版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 222.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-15 10:56:25 | ||
图片预览

文档简介
2.5 解直角三角形的应用复习 编制人:憲福数学 审核人:憲福数学 学案编号:7 时间: 2025 /2 班级 姓名
2.5 解直角三角形的应用复习
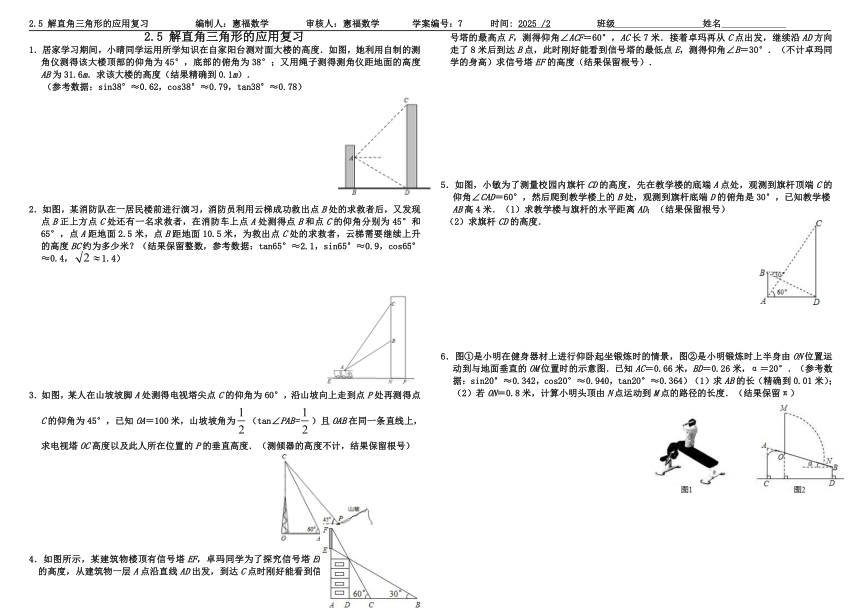
1.居家学习期间,小晴同学运用所学知识在自家阳台测对面大楼的高度.如图,她利用自制的测角仪测得该大楼顶部的仰角为45°,底部的俯角为38°;又用绳子测得测角仪距地面的高度AB为31.6m.求该大楼的高度(结果精确到0.1m).
(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
2.如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者,在消防车上点A处测得点B和点C的仰角分别为45°和65°,点A距地面2.5米,点B距地面10.5米,为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数,参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,1.4)
3.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到点P处再测得点C的仰角为45°,已知OA=100米,山坡坡角为(tan∠PAB=)且OAB在同一条直线上,求电视塔OC高度以及此人所在位置的P的垂直高度.(测倾器的高度不计,结果保留根号)
4.如图所示,某建筑物楼顶有信号塔EF,卓玛同学为了探究信号塔EF的高度,从建筑物一层A点沿直线AD出发,到达C点时刚好能看到信号塔的最高点F,测得仰角∠ACF=60°,AC长7米.接着卓玛再从C点出发,继续沿AD方向走了8米后到达B点,此时刚好能看到信号塔的最低点E,测得仰角∠B=30°.(不计卓玛同学的身高)求信号塔EF的高度(结果保留根号).
如图,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
6.图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)(1)求AB的长(精确到0.01米);(2)若ON=0.8米,计算小明头顶由N点运动到M点的路径的长度.(结果保留π)
7.如图1是一辆在平地上滑行的滑板车,如图2是其示意图.车杆BC固定,车杆AB可伸缩,车杆BC长92cm,车杆与脚踏板所成的角∠BCD=70°,前后轮子的半径均为6cm.
(1)求固定车杆BC的上端B离地面的高度.(结果保留小数点后一位)
(2)小明站在滑板车上,双手放在把手A处最舒适,此时把手A离地面的高度为120cm,求伸缩杆AB的长度.(结果保留小数点后一位;参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
8.图1是放置在水平面上的可折叠式护眼灯,其中底座的高AB=2cm,连杆BC=40cm,灯罩CD=34cm.(1)转动BC、CD,使得∠BCD成平角,且∠ABC=150°,如图2,则灯罩端点D离桌面l的高度DH是 cm.(2)将图2中的灯罩CD再绕点C顺时针旋转,使∠BCD=150°,如图3,求此时灯罩端点D离桌面l的高度DI.
9.如图,放置在水平桌面上的台灯的灯臂AB长为30cm,灯罩BC长为20cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:≈1.732)
10.如图,某数学兴趣小组利用一棵古树BH测量学校教学楼CG的高,先在A处用高1.5米的测角仪AF测得古树顶端H的仰角为45°,此时教学楼顶端G恰好在视线FH上,再向前走10米到达B处,又测得教学楼顶端G的仰角为60°,点A、B、C三点在同一水平线上.求教学楼CG的高.(结果精确到整数位,参考数据:≈1.4,≈1.7)
11.如图,花城广场对岸有广州塔AB,小明同学站在花城广场的C处看塔顶点A的仰角为32°,向塔前进360米到达点D,在D处看塔顶A的仰角为45°.
(1)求广州塔AB的高度(sin32°≈0.530,cos32°≈0.848,tan32°≈0.625);
(2)一架无人机从广州塔顶点A出发,沿水平方向AF飞行300米到A′处,求此时从A′处看点D的俯角的正切值.
12.图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.
(1)求∠ABC的度数;
(2)测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)
(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,≈1.414)
13.公园内一凉亭,凉亭顶部是一圆锥形的顶盖,立柱垂直于地面,在凉亭内中央位置有一圆形石桌,某数学研究性学习小组,将此凉亭作为研究对象,并绘制截面示意图,其中顶盖母线AB与AC的夹角为124°,凉亭顶盖边缘B、C到地面的距离为2.4米,石桌的高度DE为0.6米,经观测发现:当太阳光线与地面的夹角为42°时,恰好能够照到石桌的中央E处(A、E、D三点在一条直线上),请你求出圆锥形顶盖母线AB的长度.(结果精确到0.1m)(参考数据:sin62°≈0.88,tan42°≈0.90)
14.在同一时刻的物高与水平地面上的影长成正比例.如图,小莉发现垂直地面的电线杆AB的影子落在地面和土坡上,影长分别为BC和CD,经测量得BC=20m,CD=8m,CD与地面成30°角,且此时测得垂直于地面的1m长标杆在地面上影长为2m,求电线杆AB的长度.
2.5 解直角三角形的应用复习
1.居家学习期间,小晴同学运用所学知识在自家阳台测对面大楼的高度.如图,她利用自制的测角仪测得该大楼顶部的仰角为45°,底部的俯角为38°;又用绳子测得测角仪距地面的高度AB为31.6m.求该大楼的高度(结果精确到0.1m).
(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
2.如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者,在消防车上点A处测得点B和点C的仰角分别为45°和65°,点A距地面2.5米,点B距地面10.5米,为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数,参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,1.4)
3.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到点P处再测得点C的仰角为45°,已知OA=100米,山坡坡角为(tan∠PAB=)且OAB在同一条直线上,求电视塔OC高度以及此人所在位置的P的垂直高度.(测倾器的高度不计,结果保留根号)
4.如图所示,某建筑物楼顶有信号塔EF,卓玛同学为了探究信号塔EF的高度,从建筑物一层A点沿直线AD出发,到达C点时刚好能看到信号塔的最高点F,测得仰角∠ACF=60°,AC长7米.接着卓玛再从C点出发,继续沿AD方向走了8米后到达B点,此时刚好能看到信号塔的最低点E,测得仰角∠B=30°.(不计卓玛同学的身高)求信号塔EF的高度(结果保留根号).
如图,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
6.图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)(1)求AB的长(精确到0.01米);(2)若ON=0.8米,计算小明头顶由N点运动到M点的路径的长度.(结果保留π)
7.如图1是一辆在平地上滑行的滑板车,如图2是其示意图.车杆BC固定,车杆AB可伸缩,车杆BC长92cm,车杆与脚踏板所成的角∠BCD=70°,前后轮子的半径均为6cm.
(1)求固定车杆BC的上端B离地面的高度.(结果保留小数点后一位)
(2)小明站在滑板车上,双手放在把手A处最舒适,此时把手A离地面的高度为120cm,求伸缩杆AB的长度.(结果保留小数点后一位;参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
8.图1是放置在水平面上的可折叠式护眼灯,其中底座的高AB=2cm,连杆BC=40cm,灯罩CD=34cm.(1)转动BC、CD,使得∠BCD成平角,且∠ABC=150°,如图2,则灯罩端点D离桌面l的高度DH是 cm.(2)将图2中的灯罩CD再绕点C顺时针旋转,使∠BCD=150°,如图3,求此时灯罩端点D离桌面l的高度DI.
9.如图,放置在水平桌面上的台灯的灯臂AB长为30cm,灯罩BC长为20cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:≈1.732)
10.如图,某数学兴趣小组利用一棵古树BH测量学校教学楼CG的高,先在A处用高1.5米的测角仪AF测得古树顶端H的仰角为45°,此时教学楼顶端G恰好在视线FH上,再向前走10米到达B处,又测得教学楼顶端G的仰角为60°,点A、B、C三点在同一水平线上.求教学楼CG的高.(结果精确到整数位,参考数据:≈1.4,≈1.7)
11.如图,花城广场对岸有广州塔AB,小明同学站在花城广场的C处看塔顶点A的仰角为32°,向塔前进360米到达点D,在D处看塔顶A的仰角为45°.
(1)求广州塔AB的高度(sin32°≈0.530,cos32°≈0.848,tan32°≈0.625);
(2)一架无人机从广州塔顶点A出发,沿水平方向AF飞行300米到A′处,求此时从A′处看点D的俯角的正切值.
12.图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.
(1)求∠ABC的度数;
(2)测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)
(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,≈1.414)
13.公园内一凉亭,凉亭顶部是一圆锥形的顶盖,立柱垂直于地面,在凉亭内中央位置有一圆形石桌,某数学研究性学习小组,将此凉亭作为研究对象,并绘制截面示意图,其中顶盖母线AB与AC的夹角为124°,凉亭顶盖边缘B、C到地面的距离为2.4米,石桌的高度DE为0.6米,经观测发现:当太阳光线与地面的夹角为42°时,恰好能够照到石桌的中央E处(A、E、D三点在一条直线上),请你求出圆锥形顶盖母线AB的长度.(结果精确到0.1m)(参考数据:sin62°≈0.88,tan42°≈0.90)
14.在同一时刻的物高与水平地面上的影长成正比例.如图,小莉发现垂直地面的电线杆AB的影子落在地面和土坡上,影长分别为BC和CD,经测量得BC=20m,CD=8m,CD与地面成30°角,且此时测得垂直于地面的1m长标杆在地面上影长为2m,求电线杆AB的长度.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
