平均变化率

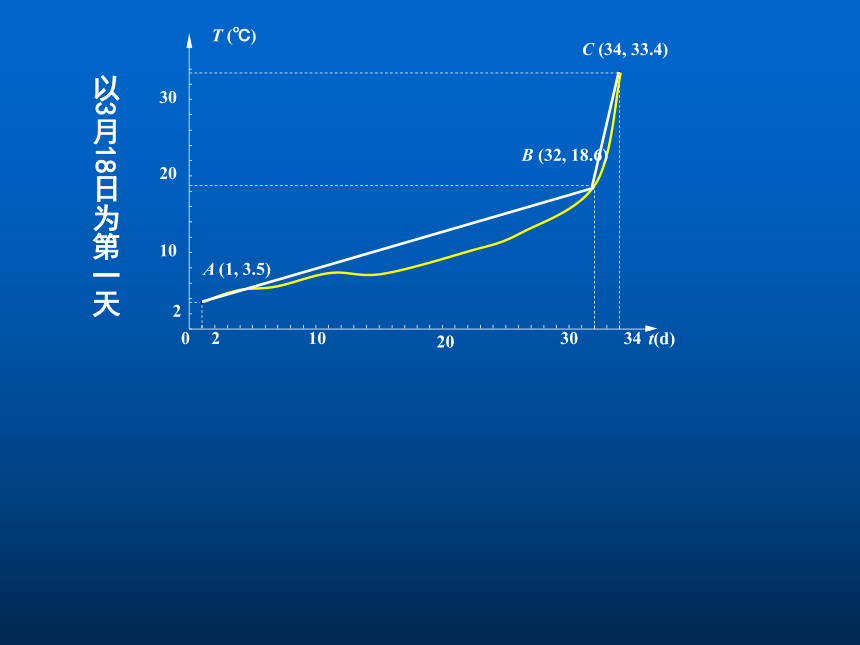
课件15张PPT。平均变化率pin jun bian hua lv苏教版选修2-2第1章第1节情境1：汽车加速性能的测定保时捷911 vs 法拉利360速度变化越快，汽车的加速性就越好。用什么数学表达式来描述汽车的速度变化的快慢?情境2：某市2004年3月和4月某天日最高气温记载.根据上面的数据我们可以得到哪些信息? t(d)2030342102030A (1, 3.5)B (32, 18.6)0C (34, 33.4)T (℃)210以3月18日为第一天总结与思考如何刻画变量f(x)在区间[x1，x2]上随x
变化（增加或减少）的“快”与“慢”？一般地，函数f(x)在区间[x1，x2]上的平均
变化率为：讨论交流:
(1)你能举出一些用函数的平均变化率刻画因变量随自变量变化“快慢”的例子吗?(2)函数平均变化率的数值如何刻画因变量随自变量变化（增加或减少）的“快慢”?例1、中华人民共和国人口普查登记的结果公布如下解：（1）1982年到1990年平均每年增加 （万人）1990年到2000年平均每年增加 （万人）(1) 1982年到1990年, 1990年到2000年, 平均每年增加多少人?(2) 1982年到1990年, 1990年到2000年, 人口的平均变化率是多少?（2）1982年到1990年人口的平均变化率为 （万人/年）1990年到2000年人口的平均变化率为 （万人/年）注: f(x)在区间[x1，x2]上的平均变化率实际上就是自变量增加一个单位,因变量的平均增量. 1953年到1964年人口的平均变化率为 （万人/年）1964年到1982年人口的平均变化率为 （万人/年）1982年到1990年人口的平均变化率为 （万人/年）1990年到2000年人口的平均变化率为 （万人/年）例2、已知函数f(x)=2x+1，g(x)=-2x，分别计算在区间[-3,-1]，[0,5]上f(x)及g(x)的平均变化率。 思考：y=kx+b在区间[m,n]上的平均变化率有什么特点？ 例3、已知函数f(x)=x2 ，分别计算在下列区间上的平均变化率：
（1）[1，2]；
（2）[2，3]；
（3）[1，3]；（4）[1，1.001]。总结
1.f(x)在区间[x1，x2]随x变化的快慢可用f(x)的平均变化率来刻画.
2. f(x)在区间[x1，x2]上的平均变化率是曲线y=f(x)在区间[x1，x2]上陡峭程度的“数量化”，曲线陡峭程度是平均变化率的“视觉化”．
3. f(x)在区间[x1，x2]上的平均变化率是在其局部区间上f(x)随x变化的快慢以及曲线y=f(x)陡峭程度的一种粗略刻画.
作业 P：7 练习1，2，3，4
思考题（选做）：
吹气球时,会发现:随着气球内空气容量的增加,气球的半径增加得越来越慢。
（1）你能从数学的角度作出解释吗？
（2）请判断下面哪个是半径r随体积v变化的示意图?
vOrv0Orv0vOrv0vr0r0r0谢谢！