数学活动 二元一次方程的“图象”及轮胎换位问题 课件(共21张PPT) 2024-2025学年人教版七年级数学下册
文档属性
| 名称 | 数学活动 二元一次方程的“图象”及轮胎换位问题 课件(共21张PPT) 2024-2025学年人教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 21.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-15 16:42:42 | ||
图片预览







文档简介
(共21张PPT)
第十章 二元一次方程组
数学活动4
二元一次方程的“图象”
及轮胎换位问题
学习目标
1.会把二元一次方程的解在平面直角坐标系中运用点的坐标表示出来.
2.能通过两条直线的交点情况确定二元一次方程组的解的情况.
3.从方程到直线,从点的坐标到方程组的解,体会数形结合思想.
4.培养学生乐于探究的钻研精神,培养几何直观、应用意识等
核心素养.
5.了解轮胎换位的实际意义,增强对数学的应用意识.
重点:二元一次方程的图象是一条直线
难点:利用图象法求二元一次方程组的解.
我们知道坐标平面内的点与有序实数对是一一对应的,那么我们能否把二元一次方程的解作为点的坐标在坐标系内找出相应的点,然后借助于图形的直观性来确定二元一次方程(组)的解与两方程对应的图象特征呢
二元一次方程的“图象“
1
思考:在平面直角坐标系中,你能把二元一次方程 x - y = 0 的一个解用一个点表示出来吗
问题1:你能说出二元一次方程 x - y = 0 的一些解吗
x = -2
y = -2
x = -1
y = -1
x = 0
y = 0
x = 1
y = 1
例:
x = 2
y = 2
问题3:标出一些以方程 x - y = 0 的解为坐标的点,过这些点中的任意两点作直线,你有什么发现
问题2:你能把二元一次方程 x - y = 0 的这些解用有序数对表示出来吗
(1,1)
(-2,-2)
(0,0)
(-1,-1)
(2,2)
这些点都在同一条直线上.
问题4:在这条直线上任取一点,这个点的坐标是方程 x - y = 0 的解吗
问题5:描出的点都在同一条直线上,你发现了什么
在这条直线上的每一个点所对应的数对刚好是方程 x - y = 0 的解.
方程 x - y = 0 的解与这条直线上的点所表示的数对刚好一一对应.
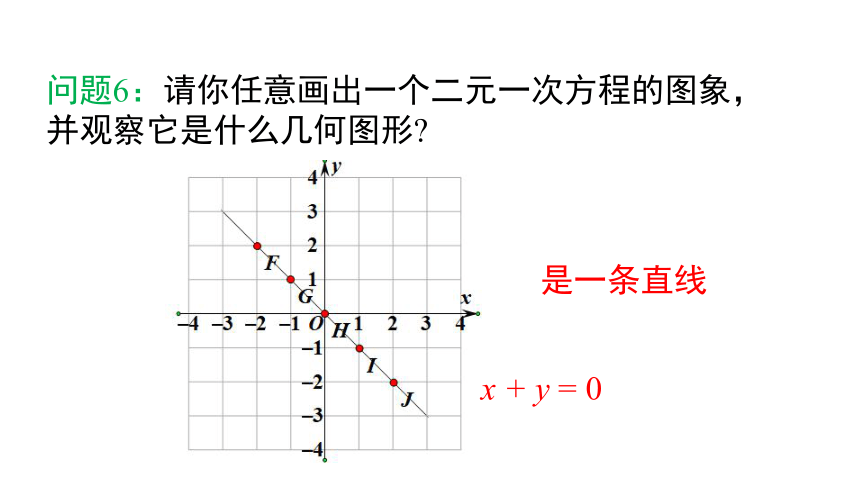
问题6:请你任意画出一个二元一次方程的图象,并观察它是什么几何图形
是一条直线
x + y = 0
2
二元一次方程组的“图象”
活动:请你在同一平面直角坐标系中画出二元一次方程组 中的两个二元一次方程的图象.
2x + y = 4,
x - y = -1
填写下面的表格:
2x+y = 4 x
y
x-y = -1 x
y
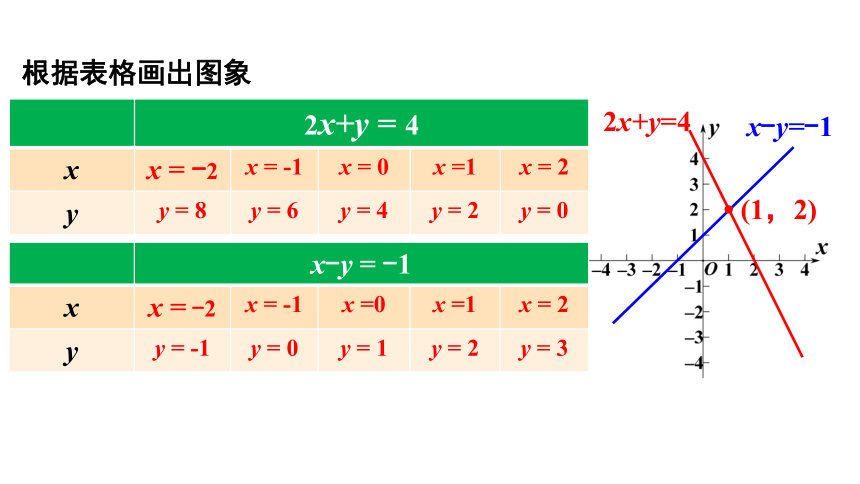
2x+y = 4 x x = -2 x = -1 x = 0 x =1 x = 2
y y = 8 y = 6 y = 4 y = 2 y = 0
x-y = -1 x x = -2 x = -1 x =0 x =1 x = 2
y y = -1 y = 0 y = 1 y = 2 y = 3
2x+y=4
x-y=-1
(1,2)
根据表格画出图象
问题2:点 A(2,0),B(0,4),
C(0,1),D(-1,0), E(1,2) 分别在哪个方程的图象上 是哪个方程的解
问题1:任何一个二元一次方程的图象都是一条直线,那么怎样快速地画出它的图象呢
可以选择在这个二元一次方程图象上的两个点,然后连接起来.
点A(2,0),B(0,4) ,E(1, 2)
在 2x + y = 4的图象上,并且是它的解.
点C(0,1),D(-1,0), E(1,2)
在 x - y = -1 的图象上,并且是它的解.
2x+y=4
x-y=-1
(1,2)
问题3:通过这两个二元一次方程的图象,你能得出这个二元一次方程组的解吗
二元一次方程组的解是满足 2x + y = 4 和 x - y = -1 两个方程的公共解,在图象上反映的就是这两个图象的交点.
两个方程的公共解
图象的交点
数
形
2x+y=4
x-y=-1
(1,2)
(1) 一般地,以一个二元一次方程的解为坐标的点的全体叫作这个方程的图象.
归纳总结
(3) 二元一次方程组两个方程的图象的交点坐标就是这个方程组的解;方程组的解就是对应两图象的交点坐标.
(2) 一般地,任何一个二元一次方程的图象都是一条直线,这条直线上的任意一点的坐标都是这个方程的解.
两条直线的交点个数有几种情况 二元一次方程组的解有几种情况 二元一次方程组的解的个数是否与两条直线的交点个数存在对应关系
(1) 两直线相交,方程组有唯一解.
(3) 两直线重合,方程组有无数个解.
(2) 两直线平行,方程组无解;方程组无解,两直线平行.
拓展思考
用二元一次方程组解决轮胎换位问题
3
资料显示:
汽车前轮轮胎一般应在汽车行驶达到 60 000 km 时报废,而后轮轮胎应在汽车行驶达到 80 000 km 时报废,如果在轮胎的使用寿命内只交换一次前、后轮胎,那么应在汽车行驶里程达到多少时,交换
前、后轮胎,能使汽车的两对轮胎同时报废 并求出轮胎报废时汽车的行驶里程.
点击视频观看
问题分析:
若设汽车新轮胎开至报废时的磨损程度为 1,前轮胎每行驶 1 km 磨损 ,后轮胎每行驶 1 km 磨损,设更换前行驶 x km,更换后行驶 y km,你能列出关于 x 和 y 满足的方程组并求出 x , y 的值吗
解得
y =
x =
问题解决:
你能求出轮胎报废时汽车的行驶里程是多少吗
(x + y) =
结论:当汽车行驶里程约为 km 时更换前后轮胎,能使汽车的两对轮胎同时报废,汽车报废时行驶里程约为 km.
你能否用其他方法来解决问题呢
(60 000 - x)·
解:设汽车行驶了 x km 后更换轮胎,由题意可列出方程:
解得
x =
还可以运用其他方法解决问题吗
1.一辆自行车换胎,若新轮胎安装在前轮,则自行车行驶2 500km后报废;若新轮胎安装在后轮,则自行车行驶1 500km后报废,如果可以在自行车行驶一定的路程后,通过交换前后轮轮胎使一辆自行车的一对新轮胎同时报废,那么这对新轮胎一共能支撑自行车行驶( )
A.1 875 km B. 1 975 km
C.2 000 km D.2 250 km
A
2.汽车轮胎如果放在前轮可以行驶 30 000 km,如果放在后轮可以行驶 50 000 km. 现有一辆汽车,允许在恰当的时候将前轮和后轮互换,如果在行驶过程中只允许前、后轮对调一次,那么最多可以行驶多少千米而不需要购买新的轮胎 应当在行驶多少千米的时候将前、后轮对调
解:设跑 x 千米后调换,继续行驶 y 千米后,所有的轮胎全部需要更换.
解得
y=18 750.
x=18 750,
答:行驶 18 750 千米后调换,最多可行驶37 500千米.
= 1
= 1
x+y=18 750+18 750=37 500(千米)
第十章 二元一次方程组
数学活动4
二元一次方程的“图象”
及轮胎换位问题
学习目标
1.会把二元一次方程的解在平面直角坐标系中运用点的坐标表示出来.
2.能通过两条直线的交点情况确定二元一次方程组的解的情况.
3.从方程到直线,从点的坐标到方程组的解,体会数形结合思想.
4.培养学生乐于探究的钻研精神,培养几何直观、应用意识等
核心素养.
5.了解轮胎换位的实际意义,增强对数学的应用意识.
重点:二元一次方程的图象是一条直线
难点:利用图象法求二元一次方程组的解.
我们知道坐标平面内的点与有序实数对是一一对应的,那么我们能否把二元一次方程的解作为点的坐标在坐标系内找出相应的点,然后借助于图形的直观性来确定二元一次方程(组)的解与两方程对应的图象特征呢
二元一次方程的“图象“
1
思考:在平面直角坐标系中,你能把二元一次方程 x - y = 0 的一个解用一个点表示出来吗
问题1:你能说出二元一次方程 x - y = 0 的一些解吗
x = -2
y = -2
x = -1
y = -1
x = 0
y = 0
x = 1
y = 1
例:
x = 2
y = 2
问题3:标出一些以方程 x - y = 0 的解为坐标的点,过这些点中的任意两点作直线,你有什么发现
问题2:你能把二元一次方程 x - y = 0 的这些解用有序数对表示出来吗
(1,1)
(-2,-2)
(0,0)
(-1,-1)
(2,2)
这些点都在同一条直线上.
问题4:在这条直线上任取一点,这个点的坐标是方程 x - y = 0 的解吗
问题5:描出的点都在同一条直线上,你发现了什么
在这条直线上的每一个点所对应的数对刚好是方程 x - y = 0 的解.
方程 x - y = 0 的解与这条直线上的点所表示的数对刚好一一对应.
问题6:请你任意画出一个二元一次方程的图象,并观察它是什么几何图形
是一条直线
x + y = 0
2
二元一次方程组的“图象”
活动:请你在同一平面直角坐标系中画出二元一次方程组 中的两个二元一次方程的图象.
2x + y = 4,
x - y = -1
填写下面的表格:
2x+y = 4 x
y
x-y = -1 x
y
2x+y = 4 x x = -2 x = -1 x = 0 x =1 x = 2
y y = 8 y = 6 y = 4 y = 2 y = 0
x-y = -1 x x = -2 x = -1 x =0 x =1 x = 2
y y = -1 y = 0 y = 1 y = 2 y = 3
2x+y=4
x-y=-1
(1,2)
根据表格画出图象
问题2:点 A(2,0),B(0,4),
C(0,1),D(-1,0), E(1,2) 分别在哪个方程的图象上 是哪个方程的解
问题1:任何一个二元一次方程的图象都是一条直线,那么怎样快速地画出它的图象呢
可以选择在这个二元一次方程图象上的两个点,然后连接起来.
点A(2,0),B(0,4) ,E(1, 2)
在 2x + y = 4的图象上,并且是它的解.
点C(0,1),D(-1,0), E(1,2)
在 x - y = -1 的图象上,并且是它的解.
2x+y=4
x-y=-1
(1,2)
问题3:通过这两个二元一次方程的图象,你能得出这个二元一次方程组的解吗
二元一次方程组的解是满足 2x + y = 4 和 x - y = -1 两个方程的公共解,在图象上反映的就是这两个图象的交点.
两个方程的公共解
图象的交点
数
形
2x+y=4
x-y=-1
(1,2)
(1) 一般地,以一个二元一次方程的解为坐标的点的全体叫作这个方程的图象.
归纳总结
(3) 二元一次方程组两个方程的图象的交点坐标就是这个方程组的解;方程组的解就是对应两图象的交点坐标.
(2) 一般地,任何一个二元一次方程的图象都是一条直线,这条直线上的任意一点的坐标都是这个方程的解.
两条直线的交点个数有几种情况 二元一次方程组的解有几种情况 二元一次方程组的解的个数是否与两条直线的交点个数存在对应关系
(1) 两直线相交,方程组有唯一解.
(3) 两直线重合,方程组有无数个解.
(2) 两直线平行,方程组无解;方程组无解,两直线平行.
拓展思考
用二元一次方程组解决轮胎换位问题
3
资料显示:
汽车前轮轮胎一般应在汽车行驶达到 60 000 km 时报废,而后轮轮胎应在汽车行驶达到 80 000 km 时报废,如果在轮胎的使用寿命内只交换一次前、后轮胎,那么应在汽车行驶里程达到多少时,交换
前、后轮胎,能使汽车的两对轮胎同时报废 并求出轮胎报废时汽车的行驶里程.
点击视频观看
问题分析:
若设汽车新轮胎开至报废时的磨损程度为 1,前轮胎每行驶 1 km 磨损 ,后轮胎每行驶 1 km 磨损,设更换前行驶 x km,更换后行驶 y km,你能列出关于 x 和 y 满足的方程组并求出 x , y 的值吗
解得
y =
x =
问题解决:
你能求出轮胎报废时汽车的行驶里程是多少吗
(x + y) =
结论:当汽车行驶里程约为 km 时更换前后轮胎,能使汽车的两对轮胎同时报废,汽车报废时行驶里程约为 km.
你能否用其他方法来解决问题呢
(60 000 - x)·
解:设汽车行驶了 x km 后更换轮胎,由题意可列出方程:
解得
x =
还可以运用其他方法解决问题吗
1.一辆自行车换胎,若新轮胎安装在前轮,则自行车行驶2 500km后报废;若新轮胎安装在后轮,则自行车行驶1 500km后报废,如果可以在自行车行驶一定的路程后,通过交换前后轮轮胎使一辆自行车的一对新轮胎同时报废,那么这对新轮胎一共能支撑自行车行驶( )
A.1 875 km B. 1 975 km
C.2 000 km D.2 250 km
A
2.汽车轮胎如果放在前轮可以行驶 30 000 km,如果放在后轮可以行驶 50 000 km. 现有一辆汽车,允许在恰当的时候将前轮和后轮互换,如果在行驶过程中只允许前、后轮对调一次,那么最多可以行驶多少千米而不需要购买新的轮胎 应当在行驶多少千米的时候将前、后轮对调
解:设跑 x 千米后调换,继续行驶 y 千米后,所有的轮胎全部需要更换.
解得
y=18 750.
x=18 750,
答:行驶 18 750 千米后调换,最多可行驶37 500千米.
= 1
= 1
x+y=18 750+18 750=37 500(千米)
同课章节目录
