5.2.1 等式的性质与方程的简单变形 课件(共47张PPT) 华师大版(2024)数学七年级下册
文档属性
| 名称 | 5.2.1 等式的性质与方程的简单变形 课件(共47张PPT) 华师大版(2024)数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 31.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-15 00:00:00 | ||
图片预览









文档简介
(共47张PPT)
第5章 一元一次方程
5.2.1
等式的基本性质与方程的简单变形
(华东师大版·七年级下)
学习目标
1.能用文字和数学符号表达等式的性质.
2.掌握等式的性质,能运用等式的性质进行等式的变形、解简单的一元一次方程,体会化归思想.
01
新课学习
Sometimes,the smallest things take up the most room in your heart. The smallest things take up the most room in your heart.
复习巩固
下列式中哪些是等式
(1)2b (2)3m-2n (3)2+3=5 (4)a+b=b+a
(5)ab+3b2-5 (6)4x2=12 (7)9x-8=10
解:(3)、(4)、(6)、(7)是等式
√
√
√
√
探究新知
你用过天平吗?用天平称物,有什么特点?
观察上图,如果在平衡的天平的两边都加(或减)同样的量,天平还保持平衡吗?
探究新知
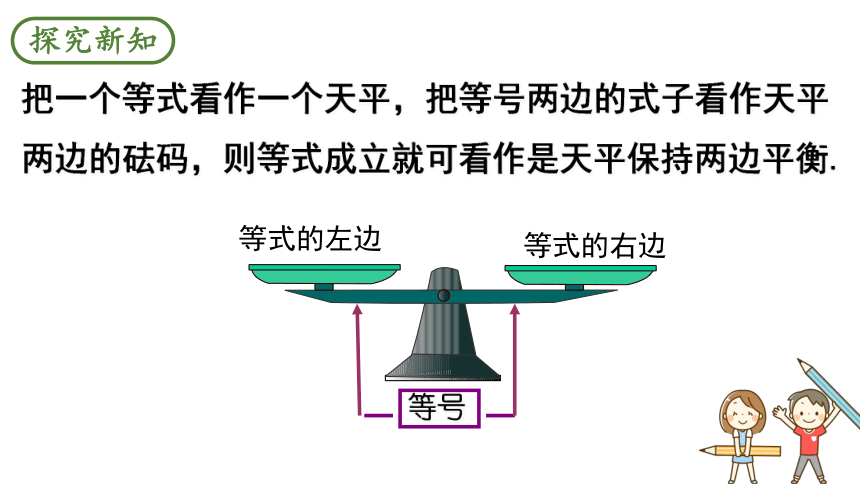
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.
等式的左边
等式的右边
等号
探究新知
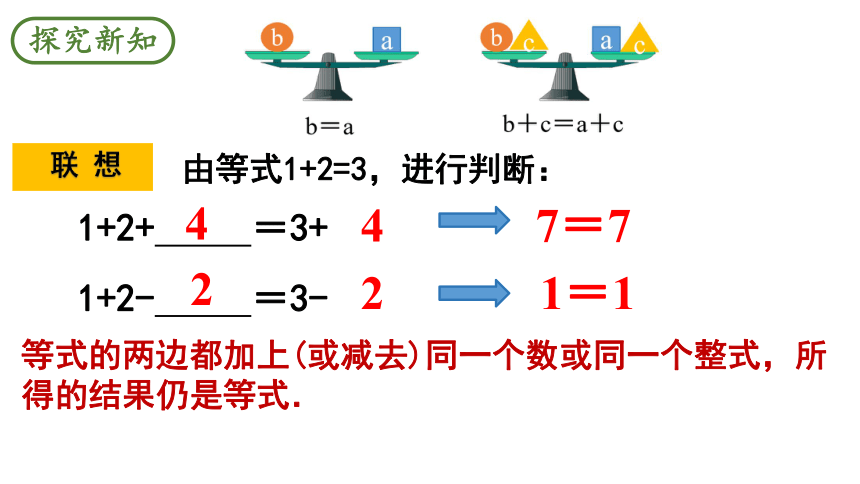
你能发现什么规律?
a
b
b
c
a
c
b=a
b+c=a+c
联 想
由等式1+2=3,进行判断:
1+2+ =3+
1+2- =3-
4
4
2
2
7=7
1=1
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
探究新知
探究新知
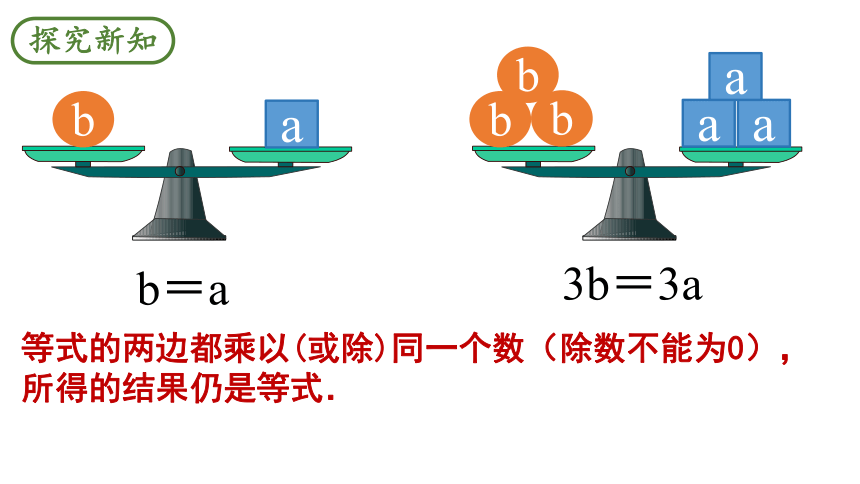
a
b
b
a
b=a
3b=3a
b
b
a
a
等式的两边都乘以(或除)同一个数(除数不能为0),所得的结果仍是等式.
一、等式的基本性质:
性质1:
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
符号语言:如果a=b,那么a+c=b+c,a-c=b-c
性质2:
等式的两边都乘以(或除)同一个数(除数不能为0),所得的结果仍是等式.
符号语言:如果a=b,那么ac=bc,=(c≠0).
典例精析
1.若a=b,则下列不一定成立的是( )
D
A.a+2=b+2 B.a=
C.a-b=0 D.a+b=0
典例精析
2.下列等式变形正确的是( )
B
A.如果x=6,那么x=3
B.如果x-3=y-2,那么x=y+1
C.如果mx=my,那么x=y
D.如果x+2=y-1,那么x+2=3y-3
典例精析
3.填空:
(1)将等式a-3=5的两边都 得到a=8,这是根据等式的基本性质 ;
(2)将等式2m=-1的两边都乘以 或除以 得到m=-,这是根据等式的基本性质 ;
(3)将等式x+y=0的两边都 得到x=-y,这是根据等式的基本性质 ;
加上3
1
减去y
探究新知
由等式的性质可以得到方程变形的规则:
1.方程两边都加上或减去同一个数或同一个整式,方程的解不变;
2.方程两边都乘以或除以同一个不为零的数,方程的解不变.
通过对方程进行适当的变形,可以求得方程的解.
探究新知
x-2=0
x=2
根据等式的基本性质,结合下面的实例,用自己的话说一说方程的变形方法
在方程的两边都加上2,可得x=2
x+2=3
x=1
在方程的两边都减去2,可得x=2
探究新知
x-2=0
x=2
根据等式的基本性质,结合下面的实例,用自己的话说一说方程的变形方法
在方程的两边都加上2,可得x=2
x+2=3
x=1
在方程的两边都减去2,可得x=2
解:
两边同时加2,
x-2+2=0+2
x=2
解:
两边同时减2,
x+2-2=3-2
x=1
探究新知
3x=2
x=
根据等式的基本性质,结合下面的实例,用自己的话说一说方程的变形方法
在方程的两边都除以3,可得x=
x=5
x=10
在方程的两边都乘以2,可得x=10
探究新知
3x=2
x=
根据等式的基本性质,结合下面的实例,用自己的话说一说方程的变形方法
在方程的两边都除以3,可得x=
x=5
x=10
在方程的两边都乘以2,可得x=10
解:
两边同时除以3,
3x÷3=2÷3
x=
解:
两边同时乘以2,
x×2=5×2
x=
典例精析
1.用适当的数或式子填空:
(1)如果2=3+x,那么x= ;
(2)如果x-y=6,那么x=6+ ;
(3)如果3x=27,那么x= ;
(4)如果=2,那么2x-1= ;
-1
y
9
10
探究新知
解下列方程:
(1)x-5=7; (2)4x=3x-4.
解:
两边都加上5,得
x=7+5
x=12
解:
两边都减去3x,得:
4x-3x=-4
x=-4
观察 思考
“– 5”这项从左边移到了右边的过程中,3x从右边移到左边有些什么变化?
改变了符号.
将方程中的某些项改变符号后,从方程的一边移到另一边,这样的变形叫做移项.
二、移项
注意
1.移动的项的位置发生了变化,同时符号也发生了改变;
2.移项是从“=”的一边移动到另一边;
3.移项要变号!
典例精析
3.下列变形属于移项且正确的是( )
A.由2x-3y+4=0,得4+2x-3y=0;
B.由3x-4=5x+2,得3x-5x=2+4;
C.由2x+4=6x+3,得2x+6x=3-4;
D.由3x-5=-3x,得3x-5-3x=0.
B
典例精析
3.解下列方程:
(1)-5x=2, (2)
解:
两边都除以-5,得
解:
两边同乘以,得
将方程中的两边同时除以未知数的系数(或乘以系数的倒数),使方程未知数系数变为1.
即
即
三、系数化1
将未知数的系数化为1是将方程的两边都除以未知数的系数,得到“x=a”的形式的变形.
典例精析
4.解下列方程:
(1)3x-3=2x+2, (2)x-2
解:
移项,得2+3
解:
移项,得
即
合并同类项,得
典例精析
5.解下列方程:
(1)2x=-8, (2)
解:
系数化1,得
解:
系数化1,得
02
课上练习
Sometimes,the smallest things take up the most room in your heart. The smallest things take up the most room in your heart.
第1题
第2题
第3题
第4题
第5题
第6题
第7题
第8题
(1)等式的基本性质
1.已知a=b,则下列式子不成立的是( )
A. a-1=b-1
B. =
C. 3a=3b
D. a-1=b+1
D
2.下列运用等式的基本性质进行变形,不正确的是( )
A.若x=t,则x-5=t-5;
B.若a=b,则ac=bc;
C.若x=y,则x+a=y+a;
D.若x=y,则4x-3=3y-3.
D
3.用“○”“□”“△”分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么“?”处应放“□”的个数为( )
A. 5 B. 4 C. 3 D. 2
A
4.有下列条件:
①a+2=b+2;
②-3a=-3b;
③-a-c=b+c;
④ac-1=bc-1.
其中根据等式的基本性质可以推导出a=b的条件有 .(填序号)
①②
5.下面是张铭同学将等式5x-3y=4x-3y变形的过程: 因为5x-3y=4x-3y,
所以5x=4x,(第一步)
所以5=4.(第二步)
上述过程中,第一步是怎样得到的?
第二步得出错误的结论,其原因是什么?
解:第一步是根据等式的基本性质1,在方程两边都加上3y得到的.
第二步错误的原因是当x=0时,两边都除以x无意义.
6.有下列变形:
①若a=b,则a;
②若a,则a=b;
③若a=b,则3a-1=3b-1;
④若,则a=b.
其中正确的是( )
A.①②③④ B.①③④ C. ①③ D.②④
B
7.下图中标有相同字母的物体的质量相同.若物体A的质量为20克,则当天平处于平衡状态时,物体B的质量为 克.
10
8.已知3b-2a-1=3a-2b,利用等式的基本性质比较a与b的大小.
解:b>a
第1题
第2题
第3题
第6题
第4题
第5题
第7题
第8题
(2)方程的简单变形
第9题
第10题
1.下列变形属于移项且正确的是( )
A.由2x=-7+x,得2x=x-7;
B.由x=y,y=0,得x=0;
C.由7x=6x-4,得7x+6x=-4;
D.由5x+4y=0,得5x=-4y.
D
2.下列解方程过程中“将未知数的系数化为1”正确的是( )
A.由4x=-5,得x=-;
B.由3x=-,得x=-;
C.由0.3x=1,得x=;
D.由-0.5x=-,得x=1.
D
3.下列变形正确的是( )
A.4x-5=3x+2变形得4x-3x=-2+5;
B.5x=-4变形得x=-;
C.6=x-3变形得x=;
D.由-0.5x=-,得x=1.
D
4.解方程2x-1=x+3,移项,得2x =3 .
5.解方程:
(1)x-3=31; (2)4x=3x-5;
-x
+1
解:
x=31+3
x=34
解:
4x-3x=-5
x=-5
5.解方程:
(3)-7x=21; (4)-x=;
解:
x=21×(-)
x=-3
解:
x=×(-)
x=-
6.已知关于x的方程2x+a-5=0的解是x=2,则a的值为( )
A. 1 B. -1
C. 9 D. -9
A
7.方程3x-4=1+2x,移项,得3x-2x=1+4,也可以理解为方程两边同时( )
A.加上(-2x+4)
B.减去(-2x+4)
C.加上(2x+4)
D.减去(2x+4)
A
8.若代数式-3是同类项,则x=
.
3
9.若关于x的方程3x- m=4x的解是x=2,求+m+1的值.
解:
将x=2代入到方程中,得6-m=8
解得,m=-4
所以+m+1=16-4+1=13
10.阅读以下例题:
解方程:|3x|=1.
解:①当3x≥0时,原方程可化为方程3x=1,它的解是x= ;
②当3x<0时,原方程可化为方程-3x=1,它的解是x=-.
所以原方程的解是x=或x=-.
仿照以上例题解方程:|2x+1|=3.
解:①当2x+1≥0时,原方程可化为方程2x+1=3,它的解是x=1 ;
②当2x+1<0时,原方程可化为方程-2x-1=1,它的解是x=0.
第5章 一元一次方程
5.2.1
等式的基本性质与方程的简单变形
(华东师大版·七年级下)
学习目标
1.能用文字和数学符号表达等式的性质.
2.掌握等式的性质,能运用等式的性质进行等式的变形、解简单的一元一次方程,体会化归思想.
01
新课学习
Sometimes,the smallest things take up the most room in your heart. The smallest things take up the most room in your heart.
复习巩固
下列式中哪些是等式
(1)2b (2)3m-2n (3)2+3=5 (4)a+b=b+a
(5)ab+3b2-5 (6)4x2=12 (7)9x-8=10
解:(3)、(4)、(6)、(7)是等式
√
√
√
√
探究新知
你用过天平吗?用天平称物,有什么特点?
观察上图,如果在平衡的天平的两边都加(或减)同样的量,天平还保持平衡吗?
探究新知
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.
等式的左边
等式的右边
等号
探究新知
你能发现什么规律?
a
b
b
c
a
c
b=a
b+c=a+c
联 想
由等式1+2=3,进行判断:
1+2+ =3+
1+2- =3-
4
4
2
2
7=7
1=1
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
探究新知
探究新知
a
b
b
a
b=a
3b=3a
b
b
a
a
等式的两边都乘以(或除)同一个数(除数不能为0),所得的结果仍是等式.
一、等式的基本性质:
性质1:
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式.
符号语言:如果a=b,那么a+c=b+c,a-c=b-c
性质2:
等式的两边都乘以(或除)同一个数(除数不能为0),所得的结果仍是等式.
符号语言:如果a=b,那么ac=bc,=(c≠0).
典例精析
1.若a=b,则下列不一定成立的是( )
D
A.a+2=b+2 B.a=
C.a-b=0 D.a+b=0
典例精析
2.下列等式变形正确的是( )
B
A.如果x=6,那么x=3
B.如果x-3=y-2,那么x=y+1
C.如果mx=my,那么x=y
D.如果x+2=y-1,那么x+2=3y-3
典例精析
3.填空:
(1)将等式a-3=5的两边都 得到a=8,这是根据等式的基本性质 ;
(2)将等式2m=-1的两边都乘以 或除以 得到m=-,这是根据等式的基本性质 ;
(3)将等式x+y=0的两边都 得到x=-y,这是根据等式的基本性质 ;
加上3
1
减去y
探究新知
由等式的性质可以得到方程变形的规则:
1.方程两边都加上或减去同一个数或同一个整式,方程的解不变;
2.方程两边都乘以或除以同一个不为零的数,方程的解不变.
通过对方程进行适当的变形,可以求得方程的解.
探究新知
x-2=0
x=2
根据等式的基本性质,结合下面的实例,用自己的话说一说方程的变形方法
在方程的两边都加上2,可得x=2
x+2=3
x=1
在方程的两边都减去2,可得x=2
探究新知
x-2=0
x=2
根据等式的基本性质,结合下面的实例,用自己的话说一说方程的变形方法
在方程的两边都加上2,可得x=2
x+2=3
x=1
在方程的两边都减去2,可得x=2
解:
两边同时加2,
x-2+2=0+2
x=2
解:
两边同时减2,
x+2-2=3-2
x=1
探究新知
3x=2
x=
根据等式的基本性质,结合下面的实例,用自己的话说一说方程的变形方法
在方程的两边都除以3,可得x=
x=5
x=10
在方程的两边都乘以2,可得x=10
探究新知
3x=2
x=
根据等式的基本性质,结合下面的实例,用自己的话说一说方程的变形方法
在方程的两边都除以3,可得x=
x=5
x=10
在方程的两边都乘以2,可得x=10
解:
两边同时除以3,
3x÷3=2÷3
x=
解:
两边同时乘以2,
x×2=5×2
x=
典例精析
1.用适当的数或式子填空:
(1)如果2=3+x,那么x= ;
(2)如果x-y=6,那么x=6+ ;
(3)如果3x=27,那么x= ;
(4)如果=2,那么2x-1= ;
-1
y
9
10
探究新知
解下列方程:
(1)x-5=7; (2)4x=3x-4.
解:
两边都加上5,得
x=7+5
x=12
解:
两边都减去3x,得:
4x-3x=-4
x=-4
观察 思考
“– 5”这项从左边移到了右边的过程中,3x从右边移到左边有些什么变化?
改变了符号.
将方程中的某些项改变符号后,从方程的一边移到另一边,这样的变形叫做移项.
二、移项
注意
1.移动的项的位置发生了变化,同时符号也发生了改变;
2.移项是从“=”的一边移动到另一边;
3.移项要变号!
典例精析
3.下列变形属于移项且正确的是( )
A.由2x-3y+4=0,得4+2x-3y=0;
B.由3x-4=5x+2,得3x-5x=2+4;
C.由2x+4=6x+3,得2x+6x=3-4;
D.由3x-5=-3x,得3x-5-3x=0.
B
典例精析
3.解下列方程:
(1)-5x=2, (2)
解:
两边都除以-5,得
解:
两边同乘以,得
将方程中的两边同时除以未知数的系数(或乘以系数的倒数),使方程未知数系数变为1.
即
即
三、系数化1
将未知数的系数化为1是将方程的两边都除以未知数的系数,得到“x=a”的形式的变形.
典例精析
4.解下列方程:
(1)3x-3=2x+2, (2)x-2
解:
移项,得2+3
解:
移项,得
即
合并同类项,得
典例精析
5.解下列方程:
(1)2x=-8, (2)
解:
系数化1,得
解:
系数化1,得
02
课上练习
Sometimes,the smallest things take up the most room in your heart. The smallest things take up the most room in your heart.
第1题
第2题
第3题
第4题
第5题
第6题
第7题
第8题
(1)等式的基本性质
1.已知a=b,则下列式子不成立的是( )
A. a-1=b-1
B. =
C. 3a=3b
D. a-1=b+1
D
2.下列运用等式的基本性质进行变形,不正确的是( )
A.若x=t,则x-5=t-5;
B.若a=b,则ac=bc;
C.若x=y,则x+a=y+a;
D.若x=y,则4x-3=3y-3.
D
3.用“○”“□”“△”分别表示三种不同的物体,如图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么“?”处应放“□”的个数为( )
A. 5 B. 4 C. 3 D. 2
A
4.有下列条件:
①a+2=b+2;
②-3a=-3b;
③-a-c=b+c;
④ac-1=bc-1.
其中根据等式的基本性质可以推导出a=b的条件有 .(填序号)
①②
5.下面是张铭同学将等式5x-3y=4x-3y变形的过程: 因为5x-3y=4x-3y,
所以5x=4x,(第一步)
所以5=4.(第二步)
上述过程中,第一步是怎样得到的?
第二步得出错误的结论,其原因是什么?
解:第一步是根据等式的基本性质1,在方程两边都加上3y得到的.
第二步错误的原因是当x=0时,两边都除以x无意义.
6.有下列变形:
①若a=b,则a;
②若a,则a=b;
③若a=b,则3a-1=3b-1;
④若,则a=b.
其中正确的是( )
A.①②③④ B.①③④ C. ①③ D.②④
B
7.下图中标有相同字母的物体的质量相同.若物体A的质量为20克,则当天平处于平衡状态时,物体B的质量为 克.
10
8.已知3b-2a-1=3a-2b,利用等式的基本性质比较a与b的大小.
解:b>a
第1题
第2题
第3题
第6题
第4题
第5题
第7题
第8题
(2)方程的简单变形
第9题
第10题
1.下列变形属于移项且正确的是( )
A.由2x=-7+x,得2x=x-7;
B.由x=y,y=0,得x=0;
C.由7x=6x-4,得7x+6x=-4;
D.由5x+4y=0,得5x=-4y.
D
2.下列解方程过程中“将未知数的系数化为1”正确的是( )
A.由4x=-5,得x=-;
B.由3x=-,得x=-;
C.由0.3x=1,得x=;
D.由-0.5x=-,得x=1.
D
3.下列变形正确的是( )
A.4x-5=3x+2变形得4x-3x=-2+5;
B.5x=-4变形得x=-;
C.6=x-3变形得x=;
D.由-0.5x=-,得x=1.
D
4.解方程2x-1=x+3,移项,得2x =3 .
5.解方程:
(1)x-3=31; (2)4x=3x-5;
-x
+1
解:
x=31+3
x=34
解:
4x-3x=-5
x=-5
5.解方程:
(3)-7x=21; (4)-x=;
解:
x=21×(-)
x=-3
解:
x=×(-)
x=-
6.已知关于x的方程2x+a-5=0的解是x=2,则a的值为( )
A. 1 B. -1
C. 9 D. -9
A
7.方程3x-4=1+2x,移项,得3x-2x=1+4,也可以理解为方程两边同时( )
A.加上(-2x+4)
B.减去(-2x+4)
C.加上(2x+4)
D.减去(2x+4)
A
8.若代数式-3是同类项,则x=
.
3
9.若关于x的方程3x- m=4x的解是x=2,求+m+1的值.
解:
将x=2代入到方程中,得6-m=8
解得,m=-4
所以+m+1=16-4+1=13
10.阅读以下例题:
解方程:|3x|=1.
解:①当3x≥0时,原方程可化为方程3x=1,它的解是x= ;
②当3x<0时,原方程可化为方程-3x=1,它的解是x=-.
所以原方程的解是x=或x=-.
仿照以上例题解方程:|2x+1|=3.
解:①当2x+1≥0时,原方程可化为方程2x+1=3,它的解是x=1 ;
②当2x+1<0时,原方程可化为方程-2x-1=1,它的解是x=0.
