数学:14.2《三垂线定理》课件(沪教版高三上)
文档属性
| 名称 | 数学:14.2《三垂线定理》课件(沪教版高三上) |

|
|
| 格式 | rar | ||
| 文件大小 | 170.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-01 14:13:00 | ||
图片预览


文档简介
课件19张PPT。三 垂 线 定 理复习巩固1、直线和平面垂直的判定定理为
2、①过平面外一点向这个平面引垂线,垂足叫做这个点在 这个平面内的 。
②一条直线和一个平面相交,但不和这个平面垂直,那么这条直线叫做这个平面的 。
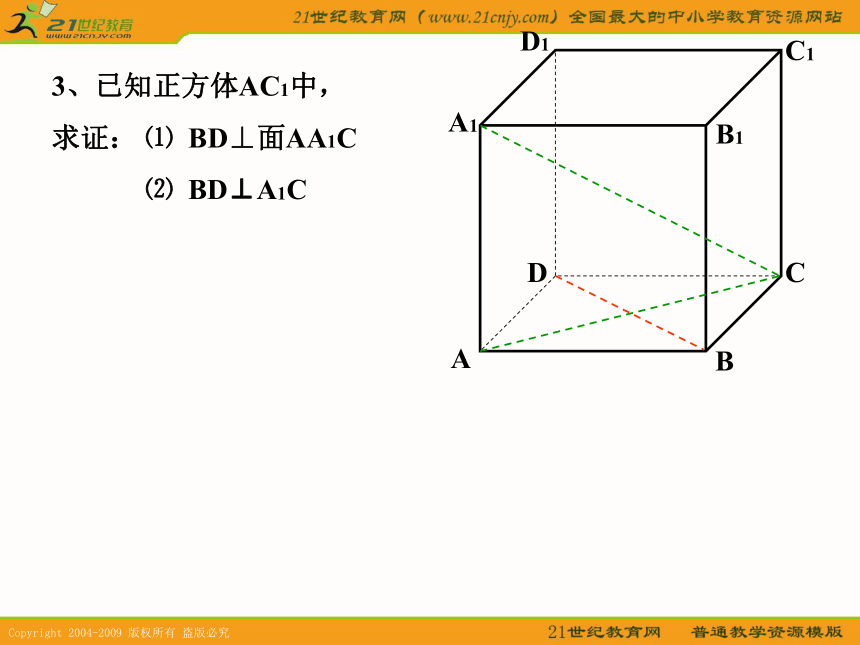
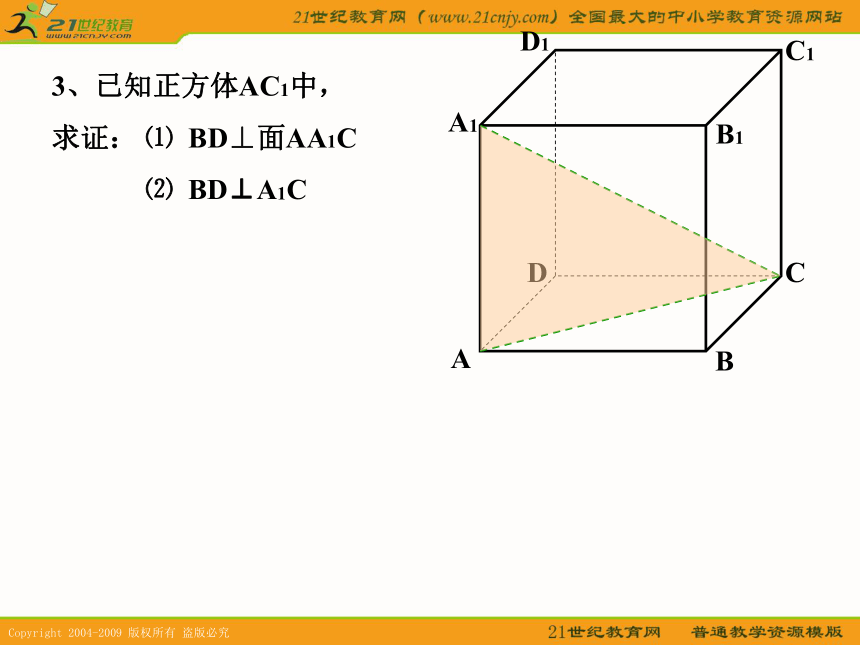
③从斜线上斜足以外的一点向平面引垂线,经过垂足和斜足的直线叫 。如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面射影斜线直线在平面上的射影3、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
⑵ BD⊥A1C3、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
⑵ BD⊥A1C
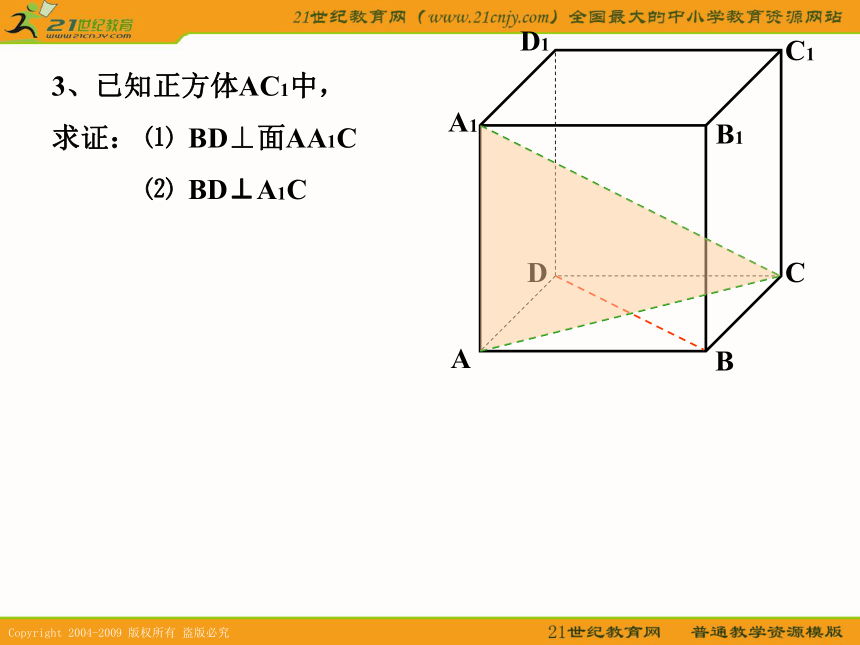
3、已知正方体AC1中,
求证:⑴ BD⊥面AA1C
⑵ BD⊥A1C
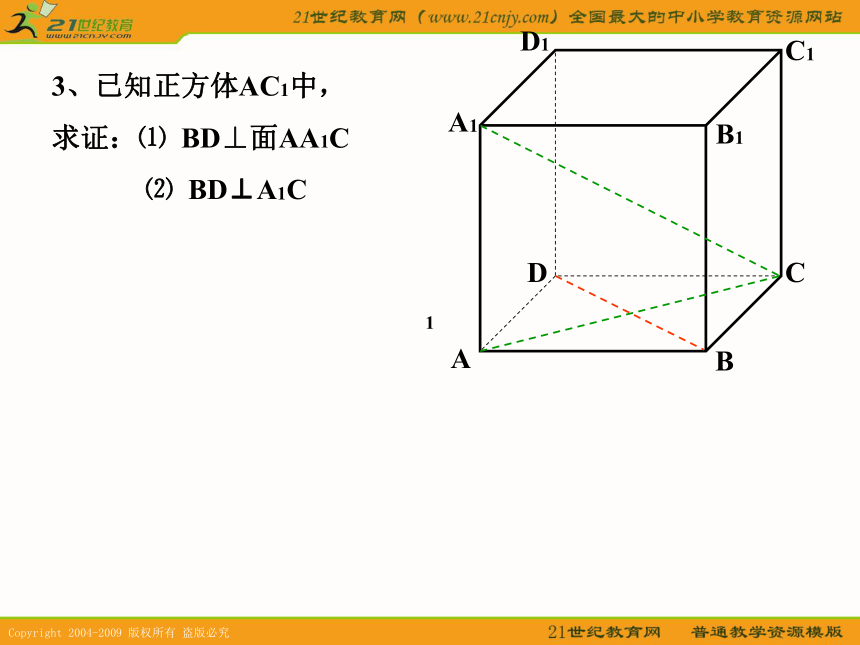
13、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
⑵ BD⊥A1C3、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
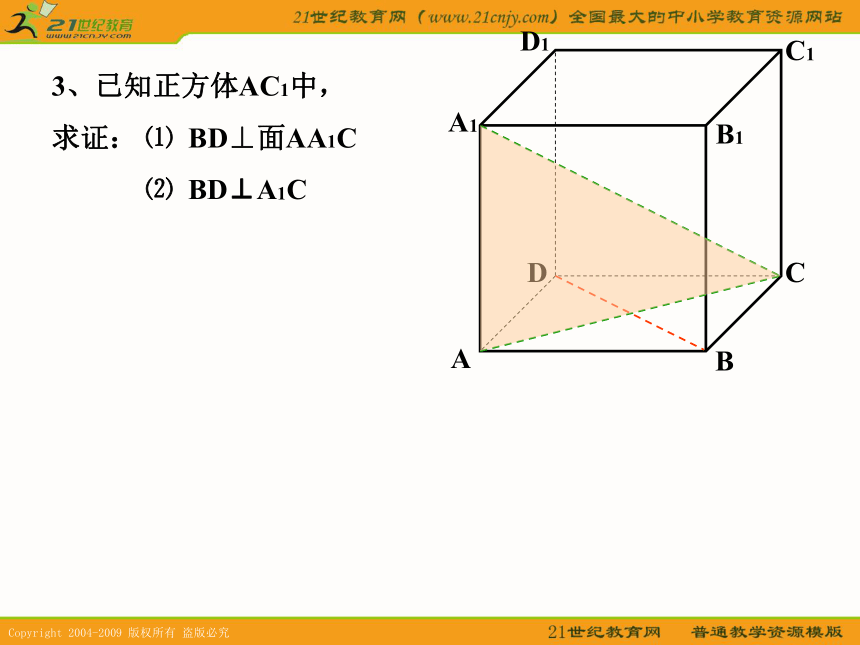
⑵ BD⊥A1C3、已知正方体AC1中,
求证:⑴ BD⊥面AA1C
⑵ BD⊥A1C
3、已知正方体AC1中,
求证:⑴ BD⊥面AA1C
⑵ BD⊥A1C
3、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
⑵ BD⊥A1C
3、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
⑵ BD⊥A1C证明:证明:⑴在正方体AC1中,AA1⊥面ABCD ∴AA1⊥BD
又BD⊥AC AC∩AA1=A
∴BD ⊥面AA1C
⑵ 由⑴知BD ⊥面AA1C A1C在面AA1C ∴BD⊥A1C
4、在正方体AC1中,AC1在平面ABCD、BB1C1C内的射影分别( )
平面 ABCD、BB1C1C内 的 直线BD、BC1分别 与 对应的斜线是否垂直?与对应的射影呢? AC、B1C垂直在平面内的一条直线、如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。已知:PO、PA分别是平面α的 垂线、斜线, OA是 PA在平面α内的射影,且a在平面α 内, a ⊥ OA
求证: a ⊥PA三垂线定理证明:∵PO⊥平面α 垂 且a在平面α内∴PO ⊥ a
又a⊥ OA OA ∩ PO=O ∴a⊥面 PAO
∴a ⊥PA
注意 关键:⑴ 寻找“垂面”
⑵ 确定“射影”
⑶判别“垂直”三线:斜线、射影、面内一条直线三垂线定理的逆定理 在平面内的一条直线、如果它和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。
三垂线定理及其逆定理
已知:如 图,正方体AC1中,E、F分别为棱AB、BC的中点
求证:C1E⊥DF例:证明:正方形ABCD 中,E、F
分别为AB、BC中点,∴△DCF≌△CBE.
∠CDF= ∠BCE 又∠CDF+ ∠DFC=900 ∴ ∠BCE+ ∠DFC=900 ∴ DF⊥CE 又因为CC1 ⊥平ABCD ∴C1E在平面ABCD 内的射影为CE。 由三垂线定理知 C1E ⊥DF
小结三垂线定理:⊥在平面内的一条直线、如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。练习和作业1、已知:O为正方体AC1的底面ABCD的中点。求证:D1O⊥EF
2、已知P为△ABC所在平面外一点, 若P在平面ABC 内的射影是△ABC的垂心。
求证:PA⊥BC PB⊥AC PC⊥AB
3、如图,PO是平面α 的斜线,O为斜足,PA⊥α于A,OC在平面 α内ABDC于B若PO与平面 α 成300角 ,∠AOB=450。PA=2cm求:
⑴PB的长
⑵∠POB的大小再见
2、①过平面外一点向这个平面引垂线,垂足叫做这个点在 这个平面内的 。
②一条直线和一个平面相交,但不和这个平面垂直,那么这条直线叫做这个平面的 。
③从斜线上斜足以外的一点向平面引垂线,经过垂足和斜足的直线叫 。如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面射影斜线直线在平面上的射影3、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
⑵ BD⊥A1C3、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
⑵ BD⊥A1C
3、已知正方体AC1中,
求证:⑴ BD⊥面AA1C
⑵ BD⊥A1C
13、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
⑵ BD⊥A1C3、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
⑵ BD⊥A1C3、已知正方体AC1中,
求证:⑴ BD⊥面AA1C
⑵ BD⊥A1C
3、已知正方体AC1中,
求证:⑴ BD⊥面AA1C
⑵ BD⊥A1C
3、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
⑵ BD⊥A1C
3、已知正方体AC1中,
求证: ⑴ BD⊥面AA1C
⑵ BD⊥A1C证明:证明:⑴在正方体AC1中,AA1⊥面ABCD ∴AA1⊥BD
又BD⊥AC AC∩AA1=A
∴BD ⊥面AA1C
⑵ 由⑴知BD ⊥面AA1C A1C在面AA1C ∴BD⊥A1C
4、在正方体AC1中,AC1在平面ABCD、BB1C1C内的射影分别( )
平面 ABCD、BB1C1C内 的 直线BD、BC1分别 与 对应的斜线是否垂直?与对应的射影呢? AC、B1C垂直在平面内的一条直线、如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。已知:PO、PA分别是平面α的 垂线、斜线, OA是 PA在平面α内的射影,且a在平面α 内, a ⊥ OA
求证: a ⊥PA三垂线定理证明:∵PO⊥平面α 垂 且a在平面α内∴PO ⊥ a
又a⊥ OA OA ∩ PO=O ∴a⊥面 PAO
∴a ⊥PA
注意 关键:⑴ 寻找“垂面”
⑵ 确定“射影”
⑶判别“垂直”三线:斜线、射影、面内一条直线三垂线定理的逆定理 在平面内的一条直线、如果它和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。
三垂线定理及其逆定理
已知:如 图,正方体AC1中,E、F分别为棱AB、BC的中点
求证:C1E⊥DF例:证明:正方形ABCD 中,E、F
分别为AB、BC中点,∴△DCF≌△CBE.
∠CDF= ∠BCE 又∠CDF+ ∠DFC=900 ∴ ∠BCE+ ∠DFC=900 ∴ DF⊥CE 又因为CC1 ⊥平ABCD ∴C1E在平面ABCD 内的射影为CE。 由三垂线定理知 C1E ⊥DF
小结三垂线定理:⊥在平面内的一条直线、如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。练习和作业1、已知:O为正方体AC1的底面ABCD的中点。求证:D1O⊥EF
2、已知P为△ABC所在平面外一点, 若P在平面ABC 内的射影是△ABC的垂心。
求证:PA⊥BC PB⊥AC PC⊥AB
3、如图,PO是平面α 的斜线,O为斜足,PA⊥α于A,OC在平面 α内ABDC于B若PO与平面 α 成300角 ,∠AOB=450。PA=2cm求:
⑴PB的长
⑵∠POB的大小再见
