数学:14.4《平面与平面垂直》课件(沪教版高三上)
文档属性
| 名称 | 数学:14.4《平面与平面垂直》课件(沪教版高三上) |

|
|
| 格式 | rar | ||
| 文件大小 | 211.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-01 00:00:00 | ||
图片预览




文档简介
课件15张PPT。空间中的垂直关系
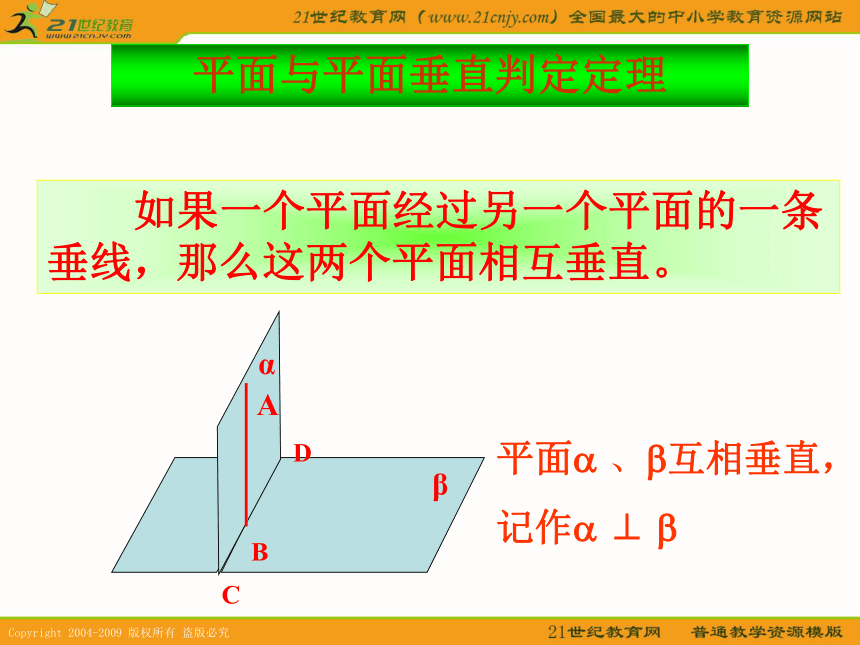
第二课时 平面与平面的垂直引入它就是本节课的内容之一:平面与平面垂直的判定定理。 建筑工人砌墙时,常用一端系有铅锤的线来检查所砌的墙面是否和地面垂直,如果系有铅锤的线和墙面紧贴,那么所砌的墙面与地面垂直。大家知道其中的理论根据吗?平面与平面垂直判定定理 如果一个平面经过另一个平面的一条垂线,那么这两个平面相互垂直。αβABCD平面? 、?互相垂直,
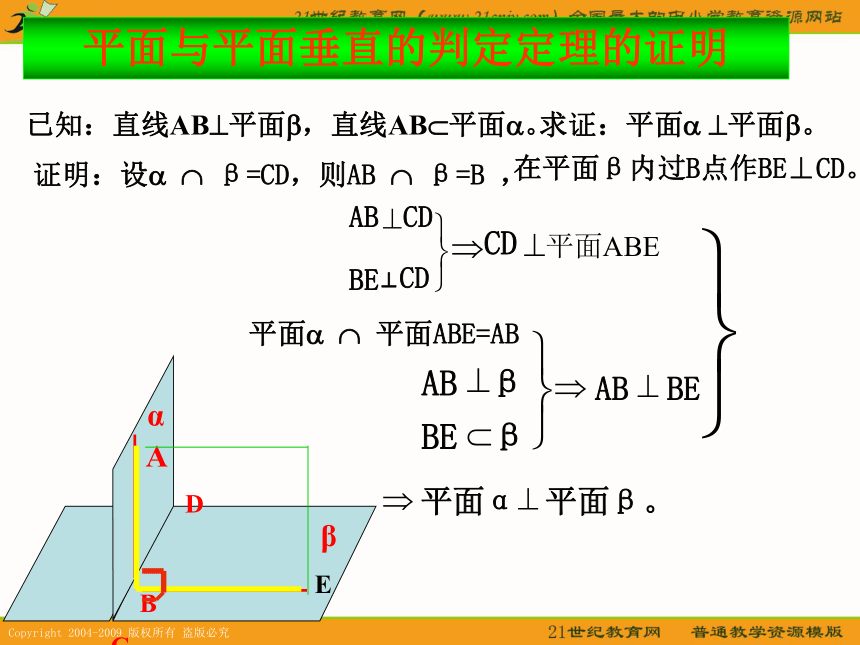
记作? ⊥ ?在平面β内过B点作BE⊥CD。平面与平面垂直的判定定理的证明已知:直线AB?平面?,直线AB?平面?。求证:平面? ?平面?。Etyü^⊥CDBECDABCD^平面ABET平面? ? 平面ABE=AB 平面与平面的垂直判定定理小结两个相交的平面的交线与第三个面垂直说明线面垂直面面垂直的判定方法:1、定义法:2、判定定理:要证两个平面垂直,另一个平面的一条垂线。只要在其中一个平面内找到(线面垂直?面面垂直)原来的两个平面与第三个平面的交线垂直线线垂直线面垂直
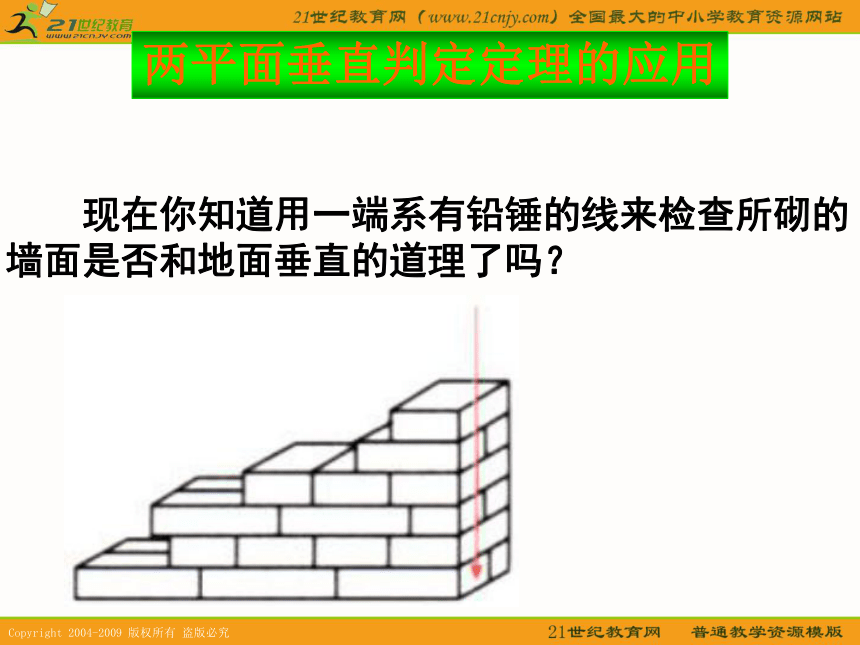
线线垂直面面垂直两平面垂直判定定理的应用 现在你知道用一端系有铅锤的线来检查所砌的
墙面是否和地面垂直的道理了吗?在刚才的命题中,直线AB,平面? ,平面?有以下三种关系:如果仍然选取其中两个条件作为前提,另一个条件作为结论请判断命题的真假。构造这样的一个命题:两平面垂直性质定理的探索两平面垂直性质定理的探索那么在已有条件的基础上,再添加什么条件,可使命题为真? 该命题是假命题!由平面? ?平面?,平面? 内的直线AB不一定能与平面?垂直。若增加条件AB?CD,则命题为真吗?两平面垂直性质定理的探索问题结论证明 过程发现猜想注证明两平面垂直的性质定理的证明已知:平面? ⊥平面β,? ∩β=CD,求证:AB⊥β。AB⊥CD,B为垂足。AB 平面? ,E证明:在平面β内过点B作BE⊥CD.
因为 ? ⊥ β,
所以 AB⊥BE.
又因为 AB⊥CD,CD ∩BE=B,
所以 AB⊥β.问题证明结论证明过程发现猜想注结论两平面垂直性质定理 如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。αβABCD面面垂直?线面垂直;平面? ⊥平面β,要过平面? 内一点引平面β的垂线,只需过这一点在平面? 内作交线的垂线。(线是一个平面内垂直于两平面交线的一条直线)ABAB两平面垂直性质定理小结应用例3 已知:如图,平面?⊥平面β ,在? 与β的交线上取线段AB=4cm,AC、BD分
别在平面?和平面β内,它们都垂直于交线AB,并且AC= 3cm ,BD=12cm,求CD长。解:连接BC.
因为 AC⊥AB,所以 AC ⊥ β,AC ⊥BD.
因为 BD ⊥AB,直线AB是两个互相垂直的平面?和β的交线,
所以 BD ⊥ ?,BD⊥BC.
在直角△BAC中,
在直角△CBD中,
所以 CD长为13cm.ABCD课堂小结2、“转化思想”线面关系线线关系面面关系线面平行线线平行线面垂直线线垂直面面垂直面面平行1、两个平面垂直的判定定理和性质定3、平面? ⊥平面β,要过平面? 内一点引平面β的垂线,只需过这一点在平面? 内作交线的垂线。课后思考在刚才的三个条件中,请判断命题的真假。若是真命题,请给出证明;若不是,那么添加什么条件可使命题为真?再选取两个条件作为前提,另一个条件作为结论构造命题,即
记作? ⊥ ?在平面β内过B点作BE⊥CD。平面与平面垂直的判定定理的证明已知:直线AB?平面?,直线AB?平面?。求证:平面? ?平面?。Etyü^⊥CDBECDABCD^平面ABET平面? ? 平面ABE=AB 平面与平面的垂直判定定理小结两个相交的平面的交线与第三个面垂直说明线面垂直面面垂直的判定方法:1、定义法:2、判定定理:要证两个平面垂直,另一个平面的一条垂线。只要在其中一个平面内找到(线面垂直?面面垂直)原来的两个平面与第三个平面的交线垂直线线垂直线面垂直
线线垂直面面垂直两平面垂直判定定理的应用 现在你知道用一端系有铅锤的线来检查所砌的
墙面是否和地面垂直的道理了吗?在刚才的命题中,直线AB,平面? ,平面?有以下三种关系:如果仍然选取其中两个条件作为前提,另一个条件作为结论请判断命题的真假。构造这样的一个命题:两平面垂直性质定理的探索两平面垂直性质定理的探索那么在已有条件的基础上,再添加什么条件,可使命题为真? 该命题是假命题!由平面? ?平面?,平面? 内的直线AB不一定能与平面?垂直。若增加条件AB?CD,则命题为真吗?两平面垂直性质定理的探索问题结论证明 过程发现猜想注证明两平面垂直的性质定理的证明已知:平面? ⊥平面β,? ∩β=CD,求证:AB⊥β。AB⊥CD,B为垂足。AB 平面? ,E证明:在平面β内过点B作BE⊥CD.
因为 ? ⊥ β,
所以 AB⊥BE.
又因为 AB⊥CD,CD ∩BE=B,
所以 AB⊥β.问题证明结论证明过程发现猜想注结论两平面垂直性质定理 如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。αβABCD面面垂直?线面垂直;平面? ⊥平面β,要过平面? 内一点引平面β的垂线,只需过这一点在平面? 内作交线的垂线。(线是一个平面内垂直于两平面交线的一条直线)ABAB两平面垂直性质定理小结应用例3 已知:如图,平面?⊥平面β ,在? 与β的交线上取线段AB=4cm,AC、BD分
别在平面?和平面β内,它们都垂直于交线AB,并且AC= 3cm ,BD=12cm,求CD长。解:连接BC.
因为 AC⊥AB,所以 AC ⊥ β,AC ⊥BD.
因为 BD ⊥AB,直线AB是两个互相垂直的平面?和β的交线,
所以 BD ⊥ ?,BD⊥BC.
在直角△BAC中,
在直角△CBD中,
所以 CD长为13cm.ABCD课堂小结2、“转化思想”线面关系线线关系面面关系线面平行线线平行线面垂直线线垂直面面垂直面面平行1、两个平面垂直的判定定理和性质定3、平面? ⊥平面β,要过平面? 内一点引平面β的垂线,只需过这一点在平面? 内作交线的垂线。课后思考在刚才的三个条件中,请判断命题的真假。若是真命题,请给出证明;若不是,那么添加什么条件可使命题为真?再选取两个条件作为前提,另一个条件作为结论构造命题,即
