华师大版七年级下册数学第五章 5.2.2 解含有括号的一元一次方程(共27张PPT)
文档属性
| 名称 | 华师大版七年级下册数学第五章 5.2.2 解含有括号的一元一次方程(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-15 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
第5章 一元一次方程
5.2.2
解含有括号的一元一次方程
(华东师大版·七年级下)
学习目标
1.了解一元一次方程的概念.
2.会用去括号的方法解一元一次方程,进一步体会等式变形中 的化归思想.
01
新课学习
Sometimes,the smallest things take up the most room in your heart. The smallest things take up the most room in your heart.
新知导入
有几人打算一起凑钱买件东西,如果他们每人出6钱,则多出7钱;如果每个人出4钱,则多出1钱.问一共有几人?(请列出方程不用求解)
解:设一共有x人.
等量关系:
一共的钱-多出的钱=东西的价格
由题意,得
6x-7=4x-1
新知导入
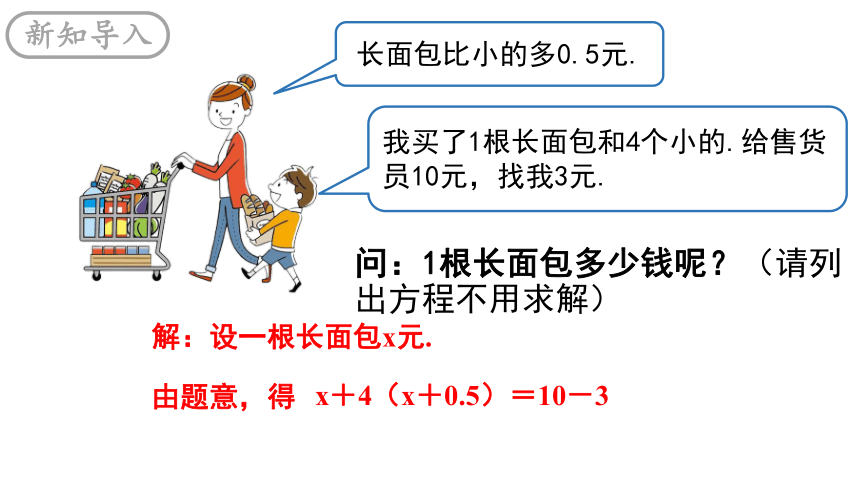
我买了1根长面包和4个小的.给售货员10元,找我3元.
长面包比小的多0.5元.
问:1根长面包多少钱呢?(请列出方程不用求解)
解:设一根长面包x元.
由题意,得
x+4(x+0.5)=10-3
探究新知
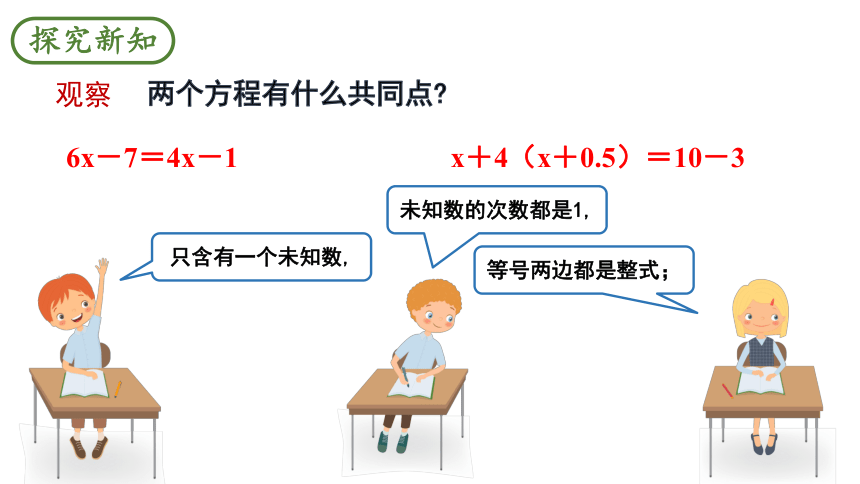
观察
两个方程有什么共同点
6x-7=4x-1
x+4(x+0.5)=10-3
只含有一个未知数,
未知数的次数都是1,
等号两边都是整式;
一、一元一次方程定义:
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做一元一次方程.
注意:
(1)一元一次方程的最简形式为:ax=b(a≠0).
(2)一元一次方程的标准形式为:ax+b =0
(其中x是未知数,a、b是已知数,并且a≠0)
典例精析
1.哪些是一元一次方程?
(1); (2)3a+9>15;
(3)2x+1 ; (4)2m+15=3;
(5)3x-5=5x+4 ; (6).
(7)-3x+1.8=3y
√
√
2.若关于x的方程是一元一次方程,则a= .
-2
探究新知
解方程:3(x-2)+1=x-(2x-1)
解:
打开括号,得
3x-6+1=x-2x+1
移项,得
3x-x+2x=1+6-1
合并同类项,得
4x=6
系数化1,得
x=
探究新知
解方程:2x-(x+10)=5x+2(x-1)
解:
打开括号,得
2x-x-10=5x+2x-2
移项,得
2x-x-5x-2x=-2+10
合并同类项,得
-6x=8
系数化1,得
x=
探究新知
解方程:3x-7(x-1)=3-2(x+3)
解:
打开括号,得
3x-7x+7=3-2x-6
移项,得
3x-7x+2x=3-6-7
合并同类项,得
-2x=-10
系数化1,得
x=
通过以上解方程的过程,你能总结出解含有括号一元一次方程的一般步骤吗?
去括号
移 项
合并同类项
系数化为1
02
课上练习
Sometimes,the smallest things take up the most room in your heart. The smallest things take up the most room in your heart.
第1题
第2题
第3题
第4题
第5题
第6题
第7题
第8题
第11题
第10题
第9题
第12题
第13题
第14题
第15题
1.下列各式中是一元一次方程的是( )
A. 1-=2y-3
B. 3 -4x=x-1
C. =+1
D. 3(2x-1)-2(1-x)=0
C
2.解方程2(x-1)-(x+2)=12,去括号正确的是( )
A. 2x-1-x+2=12 B. 2x-2-x+2=12
C. 2x-1-x-2=12 D. 2x-2-x-2=12
D
3.已知方程是关于x的一元一次方程,则n的值为( )
A. 1 B. -1 C. D. 0
B
4.若代数式3a+1与3(a+1)的值互为相反数,则a的值为( )
A. - B. - C. D.
A
5.解方程4(x-1)-x=2(x+)的步骤如下:
①去括号,得4x-4-x=2x+1;②移项,得4x+x-2x=1+4;
③合并同类项,得3x=5;④系数化为1,得x=.经检验,x=不是原方程的解,说明解题的四个步骤中有错误,其中开始出错的一步是( )
A.① B.② C. ③ D.④
B
6.已知此方程
的解是 .
7.方程2(100-15x)=60+5x的解是 .
x=
x=
8.解下列方程:
(1)8-4(x-3)=6x; (2)3(2x-1)-2(1-x)=0.
解:
8-4x+12=6x
-4x-6x=-12-8
-10x=-20
x=2
解:
6x-3-2+2x=0
6x+2x=3+2
8x=5
x=
9.用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=.若(1-3x)☆(-4)=32,则x的值为( )
A. - B. - C. D.
10.若x=4是关于x的方程3(x-2t)+2x=3t-4的解,则t= .
11.设M=2y-2,N=3y+1,且M-2N=4,则y= .
B
-2
12.解下列方程:
(1)5(x+7)-2=2x-3(x-1);
解:
5x+35-2=2x-3x+3
5x-2x+3x=3-35+2
6x=-30
x=-5
12.解下列方程:
(2)3x-[3(x+1)-(1+4x)]=1;
解:
3x-[3x+3-1-4x]=1
3x-3x-3+1+4x=1
4x=1+3-1
4x=3
x=
13.若方程12-3(x+1)=7-x的解与关于x的方程6-2k=2(x+3)的解相同,求k的值.
解:
12-3(x+1)=7-x
解得
x=1
把x=1代入方程6-2k=2(x+3)中,
6-2k=2(1+3)
解得
k=-1
14.已知,,解答下列问题:
(1)当时,求x的值;
(2)当x取何值时,的值比的值小-3?
解:
(1)由题意,可列
6-x=2(2+7x)
解得
x=
(2)由题意,可列
6-x=2+7x-3
解得
x=
15.一题多解是培养我们发散思维的重要方法,方程“6(4x-3)+2(3-4x)=3(4x-3)+5”可以有多种不同的解法,观察此方程,假设4x-3=y.
(1)原方程可变形为关于y的方程: ,通过先求y的值,从而可得x= .
(2)利用上述方法解方程:3(x-1)-(x-1)=2(x-1)-(x+1).
6y-2y=3y+5
2
解:
设x-1=y
原方程可变形为,
3y-y=2y-y
解得,
y=-
所以x-1=-
解得x=-
第5章 一元一次方程
5.2.2
解含有括号的一元一次方程
(华东师大版·七年级下)
学习目标
1.了解一元一次方程的概念.
2.会用去括号的方法解一元一次方程,进一步体会等式变形中 的化归思想.
01
新课学习
Sometimes,the smallest things take up the most room in your heart. The smallest things take up the most room in your heart.
新知导入
有几人打算一起凑钱买件东西,如果他们每人出6钱,则多出7钱;如果每个人出4钱,则多出1钱.问一共有几人?(请列出方程不用求解)
解:设一共有x人.
等量关系:
一共的钱-多出的钱=东西的价格
由题意,得
6x-7=4x-1
新知导入
我买了1根长面包和4个小的.给售货员10元,找我3元.
长面包比小的多0.5元.
问:1根长面包多少钱呢?(请列出方程不用求解)
解:设一根长面包x元.
由题意,得
x+4(x+0.5)=10-3
探究新知
观察
两个方程有什么共同点
6x-7=4x-1
x+4(x+0.5)=10-3
只含有一个未知数,
未知数的次数都是1,
等号两边都是整式;
一、一元一次方程定义:
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做一元一次方程.
注意:
(1)一元一次方程的最简形式为:ax=b(a≠0).
(2)一元一次方程的标准形式为:ax+b =0
(其中x是未知数,a、b是已知数,并且a≠0)
典例精析
1.哪些是一元一次方程?
(1); (2)3a+9>15;
(3)2x+1 ; (4)2m+15=3;
(5)3x-5=5x+4 ; (6).
(7)-3x+1.8=3y
√
√
2.若关于x的方程是一元一次方程,则a= .
-2
探究新知
解方程:3(x-2)+1=x-(2x-1)
解:
打开括号,得
3x-6+1=x-2x+1
移项,得
3x-x+2x=1+6-1
合并同类项,得
4x=6
系数化1,得
x=
探究新知
解方程:2x-(x+10)=5x+2(x-1)
解:
打开括号,得
2x-x-10=5x+2x-2
移项,得
2x-x-5x-2x=-2+10
合并同类项,得
-6x=8
系数化1,得
x=
探究新知
解方程:3x-7(x-1)=3-2(x+3)
解:
打开括号,得
3x-7x+7=3-2x-6
移项,得
3x-7x+2x=3-6-7
合并同类项,得
-2x=-10
系数化1,得
x=
通过以上解方程的过程,你能总结出解含有括号一元一次方程的一般步骤吗?
去括号
移 项
合并同类项
系数化为1
02
课上练习
Sometimes,the smallest things take up the most room in your heart. The smallest things take up the most room in your heart.
第1题
第2题
第3题
第4题
第5题
第6题
第7题
第8题
第11题
第10题
第9题
第12题
第13题
第14题
第15题
1.下列各式中是一元一次方程的是( )
A. 1-=2y-3
B. 3 -4x=x-1
C. =+1
D. 3(2x-1)-2(1-x)=0
C
2.解方程2(x-1)-(x+2)=12,去括号正确的是( )
A. 2x-1-x+2=12 B. 2x-2-x+2=12
C. 2x-1-x-2=12 D. 2x-2-x-2=12
D
3.已知方程是关于x的一元一次方程,则n的值为( )
A. 1 B. -1 C. D. 0
B
4.若代数式3a+1与3(a+1)的值互为相反数,则a的值为( )
A. - B. - C. D.
A
5.解方程4(x-1)-x=2(x+)的步骤如下:
①去括号,得4x-4-x=2x+1;②移项,得4x+x-2x=1+4;
③合并同类项,得3x=5;④系数化为1,得x=.经检验,x=不是原方程的解,说明解题的四个步骤中有错误,其中开始出错的一步是( )
A.① B.② C. ③ D.④
B
6.已知此方程
的解是 .
7.方程2(100-15x)=60+5x的解是 .
x=
x=
8.解下列方程:
(1)8-4(x-3)=6x; (2)3(2x-1)-2(1-x)=0.
解:
8-4x+12=6x
-4x-6x=-12-8
-10x=-20
x=2
解:
6x-3-2+2x=0
6x+2x=3+2
8x=5
x=
9.用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=.若(1-3x)☆(-4)=32,则x的值为( )
A. - B. - C. D.
10.若x=4是关于x的方程3(x-2t)+2x=3t-4的解,则t= .
11.设M=2y-2,N=3y+1,且M-2N=4,则y= .
B
-2
12.解下列方程:
(1)5(x+7)-2=2x-3(x-1);
解:
5x+35-2=2x-3x+3
5x-2x+3x=3-35+2
6x=-30
x=-5
12.解下列方程:
(2)3x-[3(x+1)-(1+4x)]=1;
解:
3x-[3x+3-1-4x]=1
3x-3x-3+1+4x=1
4x=1+3-1
4x=3
x=
13.若方程12-3(x+1)=7-x的解与关于x的方程6-2k=2(x+3)的解相同,求k的值.
解:
12-3(x+1)=7-x
解得
x=1
把x=1代入方程6-2k=2(x+3)中,
6-2k=2(1+3)
解得
k=-1
14.已知,,解答下列问题:
(1)当时,求x的值;
(2)当x取何值时,的值比的值小-3?
解:
(1)由题意,可列
6-x=2(2+7x)
解得
x=
(2)由题意,可列
6-x=2+7x-3
解得
x=
15.一题多解是培养我们发散思维的重要方法,方程“6(4x-3)+2(3-4x)=3(4x-3)+5”可以有多种不同的解法,观察此方程,假设4x-3=y.
(1)原方程可变形为关于y的方程: ,通过先求y的值,从而可得x= .
(2)利用上述方法解方程:3(x-1)-(x-1)=2(x-1)-(x+1).
6y-2y=3y+5
2
解:
设x-1=y
原方程可变形为,
3y-y=2y-y
解得,
y=-
所以x-1=-
解得x=-
