浙江省杭州市西湖区2024-2025学年九年级(上)期末数学试卷(含答案)
文档属性
| 名称 | 浙江省杭州市西湖区2024-2025学年九年级(上)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 147.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-15 15:04:22 | ||
图片预览




文档简介
浙江省杭州市西湖区2024-2025学年九年级(上)期末数学试卷
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.二次函数的图象的顶点坐标是( )
A. B. C. D.
2.如图,五线谱由等距离的五条平行横线组成,现有一条截线与五线谱交于点,,若线段,则线段的长为( )
A.
B.
C.
D.
3.如图,在中,弦,半径于点,,则的半径为( )
A.
B.
C.
D.
4.一个箱子里有个白球,个红球,个黑球,它们除颜色外其余均相同从箱子里任意摸出一个球是红球的概率为( )
A. B. C. D.
5.杭扇,素称“杭州雅扇”,与杭州丝绸、龙井茶被誉为“杭产三绝”如图,某款杭扇完全打开后的展开图为扇形,该扇形圆心角为,半径是,则扇形的面积为.
A.
B.
C.
D.
6.二次函数为常数,部分,的对应值如下表:
则下列判断中正确的是( )
A. 函数图象的开口向下 B. 当时,随的增大而增大
C. 当时, D. 最小值为
7.如图,绕点逆时针旋转得到,点恰好落在上,则的度数为( )
A.
B.
C.
D.
8.如图,已知,,,是上依逆时针顺序排列的四个点,且满足,设弦,,若的半径为,则在,值的变化过程中,下列代数式的值不变的是( )
A.
B.
C.
D.
9.已知二次函数为常数,,当时,,则二次函数的图象可能为( )
A. B.
C. D.
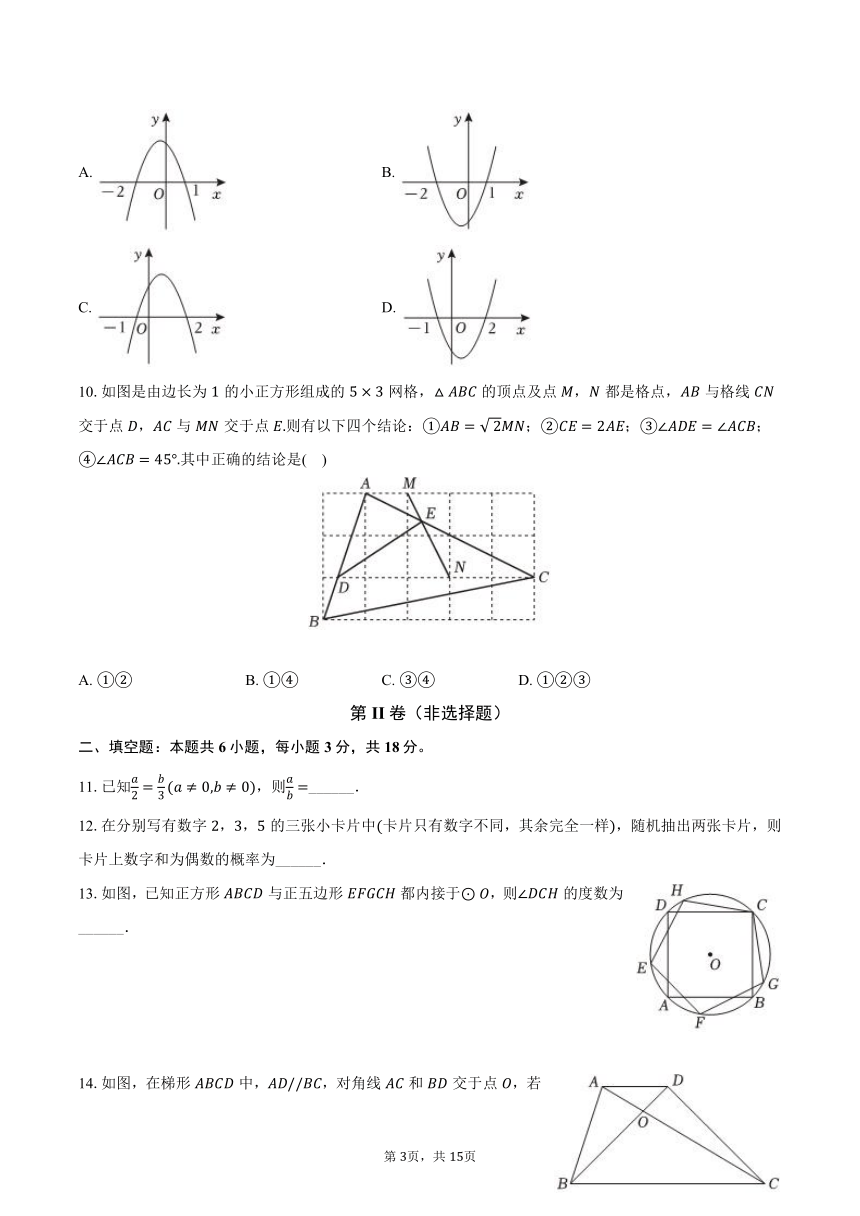
10.如图是由边长为的小正方形组成的网格,的顶点及点,都是格点,与格线交于点,与交于点则有以下四个结论:;;;其中正确的结论是( )
A. B. C. D.
第II卷(非选择题)
二、填空题:本题共6小题,每小题3分,共18分。
11.已知,则______.
12.在分别写有数字,,的三张小卡片中卡片只有数字不同,其余完全一样,随机抽出两张卡片,则卡片上数字和为偶数的概率为______.
13.如图,已知正方形与正五边形都内接于,则的度数为______.
14.如图,在梯形中,,对角线和交于点,若,则 ______.
15.已知两个不同的点,都在二次函数的图象上,则代数式的值为______.
16.如图,在中,,为上的中线,将沿直线翻折得到,与交于点,连接与,分别交于点,,连接,则 ______若,则 ______
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知二次函数的图象经过点.
求的值和二次函数的对称轴.
若把该函数图象向上平移个单位长度后与轴恰好只有一个交点,求的值.
18.本小题分
如图,在中,点,分别在边,上,连接有以下四个条件:;;;.
请你从中任选一个条件,使得∽,并说明理由.
注:如果选择多个结论分别作答,按第一个解答计分.
在的前提下,若点为中点,,求线段的长.
19.本小题分
某校开设了内容丰富的社团活动,大受同学们的欢迎.
若小丽和小红在“快乐农场”、“鲁班传人”、“花式编织”这三个社团中各随机选择个,求她们选到相同社团的概率社团名称可用,,表示
小亮参加了“快乐农场”社团,准备种植一批油麦菜,他经过大量的种子发芽实验对种子的发芽率进行了统计,得到数据如下表:
实验种子数量粒
发芽种子数量粒
种子发芽率精确到
根据表中数据,估计这批油麦菜种子的发芽率为______精确到.
社团成员在农场播种粒该批种子,估计大约能有多少粒种子发芽?
20.本小题分
已知二次函数的图象与直线经过轴上的同一点.
求二次函数的表达式.
判断二次函数图象的顶点是否在直线上,并说明理由.
若,请直接写出的取值范围.
21.本小题分
某晚,小静在相邻两盏垂直于地面的路灯,之间行走,点,为光源,影子和在线段上,图,图为示意图已知,小静的身高,于点,.
如图,当点为中点时,分别求线段,的长.
如图,当点不是中点时,设,求线段的长用含有的代数式表示
由此,你觉得与存在怎样的数量关系?
22.本小题分
综合与实践
【问题提出】
我们知道,过任意一个三角形的三个顶点能作一个圆那么,过任意一个四边形的四个顶点能作一个圆吗?
【实验探究】
获得猜想
观察图至图,分别过菱形、矩形、等腰梯形、共斜边的两个直角三角形的三个顶点作圆,提出猜想:
过______的四边形的四个顶点能作一个圆请填写序号
对边相等;一组对边平行;对角线相等;对角互补;
推理证明
已知:在四边形中,
求证:过点,,,可作一个圆.
证明:假设过点,,,不能作一个圆.
如图,过,,三点作,点不在圆上.
若点在外,
与交于点,连接,则 ______
,
而是的外角,
______出现矛盾,故假设不成立.
所以点在过,,三点的圆上.
同理可证点在内的情况.
【应用结论】
如图,四边形中,对角线,交于点,,平分.
若,求的度数.
若,,求线段的长.
23.本小题分
已知二次函数为常数图象的顶点横坐标比二次函数图象的顶点横坐标大.
求的值.
已知点在二次函数的图象上,点在二次函数的图象上.
若,求的最大值.
若,且时,始终有,求的值.
24.本小题分
如图,在正方形中,点,分别在边,上,,连接,交于点,过点,,的圆交于点,连接交于点.
证明:.
证明;
当时,求的值.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】解:把代入得,
解得,
二次函数解析式为,
,
二次函数图象的对称轴为直线;
该函数图象向上平移个单位长度后所得函数图象的解析式为,
平移后的二次函数图象与轴只有一个交点,
关于的一元二次方程有个相等的实数解,
,
解得,
即的值为.
18.【答案】解:,
理由:,,
,
,
∽.
注:答案不唯一,如选择;.
,
,
点为中点,
,
∽,
,
,
,
,
线段的长为.
19.【答案】
20.【答案】解:当时,,解得:,
二次函数的图象经过点,
二次函数;
二次函数图象的顶点在直线上;
理由:,
二次函数的顶点为,
当时,,
二次函数图象的顶点在直线上;
函数的图象如图所示:
的解集为:.
21.【答案】解:,点是中点,
,
由题可知,
,,
,,
解得,;
,
,
,
,
,
,
,
,
,
,
整理可得;
;
证明:连接,
,,
四边形是平行四边形,
,,
∽,
,
,
,
,
,
,
.
22.【答案】
23.【答案】解:函数,,
二次函数的顶点横坐标为,二次函数顶点横坐标为,
二次函数为常数图象的顶点横坐标比二次函数图象的顶点横坐标大,
,
;
点在二次函数的图象上,点在二次函数的图象上,
,,
,
,
,
时,有最大值;
,
,
,
,
,
整理得,,
即,
,,
时,始终有,
的值不会随的变化而变化,
.
24.【答案】证明:四边形是圆的内接四边形,
,
四边形是正方形,
,,
,
≌,,
,
,
≌,
,
,
,
;
证明:如图,
作,交于,
,∽,
,
由知,
,
,
,
;
解:如图,
延长,交于,作于,
,
四边形是正方形,
,,
,,
,
,
,
,
四边形是矩形,
,
,
∽,
,
,
,
,
,
,
不妨设,则,,
,
,
,
是圆的直径,
,
,
,
∽,
,
,
,
,
.
第1页,共1页
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.二次函数的图象的顶点坐标是( )
A. B. C. D.
2.如图,五线谱由等距离的五条平行横线组成,现有一条截线与五线谱交于点,,若线段,则线段的长为( )
A.
B.
C.
D.
3.如图,在中,弦,半径于点,,则的半径为( )
A.
B.
C.
D.
4.一个箱子里有个白球,个红球,个黑球,它们除颜色外其余均相同从箱子里任意摸出一个球是红球的概率为( )
A. B. C. D.
5.杭扇,素称“杭州雅扇”,与杭州丝绸、龙井茶被誉为“杭产三绝”如图,某款杭扇完全打开后的展开图为扇形,该扇形圆心角为,半径是,则扇形的面积为.
A.
B.
C.
D.
6.二次函数为常数,部分,的对应值如下表:
则下列判断中正确的是( )
A. 函数图象的开口向下 B. 当时,随的增大而增大
C. 当时, D. 最小值为
7.如图,绕点逆时针旋转得到,点恰好落在上,则的度数为( )
A.
B.
C.
D.
8.如图,已知,,,是上依逆时针顺序排列的四个点,且满足,设弦,,若的半径为,则在,值的变化过程中,下列代数式的值不变的是( )
A.
B.
C.
D.
9.已知二次函数为常数,,当时,,则二次函数的图象可能为( )
A. B.
C. D.
10.如图是由边长为的小正方形组成的网格,的顶点及点,都是格点,与格线交于点,与交于点则有以下四个结论:;;;其中正确的结论是( )
A. B. C. D.
第II卷(非选择题)
二、填空题:本题共6小题,每小题3分,共18分。
11.已知,则______.
12.在分别写有数字,,的三张小卡片中卡片只有数字不同,其余完全一样,随机抽出两张卡片,则卡片上数字和为偶数的概率为______.
13.如图,已知正方形与正五边形都内接于,则的度数为______.
14.如图,在梯形中,,对角线和交于点,若,则 ______.
15.已知两个不同的点,都在二次函数的图象上,则代数式的值为______.
16.如图,在中,,为上的中线,将沿直线翻折得到,与交于点,连接与,分别交于点,,连接,则 ______若,则 ______
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知二次函数的图象经过点.
求的值和二次函数的对称轴.
若把该函数图象向上平移个单位长度后与轴恰好只有一个交点,求的值.
18.本小题分
如图,在中,点,分别在边,上,连接有以下四个条件:;;;.
请你从中任选一个条件,使得∽,并说明理由.
注:如果选择多个结论分别作答,按第一个解答计分.
在的前提下,若点为中点,,求线段的长.
19.本小题分
某校开设了内容丰富的社团活动,大受同学们的欢迎.
若小丽和小红在“快乐农场”、“鲁班传人”、“花式编织”这三个社团中各随机选择个,求她们选到相同社团的概率社团名称可用,,表示
小亮参加了“快乐农场”社团,准备种植一批油麦菜,他经过大量的种子发芽实验对种子的发芽率进行了统计,得到数据如下表:
实验种子数量粒
发芽种子数量粒
种子发芽率精确到
根据表中数据,估计这批油麦菜种子的发芽率为______精确到.
社团成员在农场播种粒该批种子,估计大约能有多少粒种子发芽?
20.本小题分
已知二次函数的图象与直线经过轴上的同一点.
求二次函数的表达式.
判断二次函数图象的顶点是否在直线上,并说明理由.
若,请直接写出的取值范围.
21.本小题分
某晚,小静在相邻两盏垂直于地面的路灯,之间行走,点,为光源,影子和在线段上,图,图为示意图已知,小静的身高,于点,.
如图,当点为中点时,分别求线段,的长.
如图,当点不是中点时,设,求线段的长用含有的代数式表示
由此,你觉得与存在怎样的数量关系?
22.本小题分
综合与实践
【问题提出】
我们知道,过任意一个三角形的三个顶点能作一个圆那么,过任意一个四边形的四个顶点能作一个圆吗?
【实验探究】
获得猜想
观察图至图,分别过菱形、矩形、等腰梯形、共斜边的两个直角三角形的三个顶点作圆,提出猜想:
过______的四边形的四个顶点能作一个圆请填写序号
对边相等;一组对边平行;对角线相等;对角互补;
推理证明
已知:在四边形中,
求证:过点,,,可作一个圆.
证明:假设过点,,,不能作一个圆.
如图,过,,三点作,点不在圆上.
若点在外,
与交于点,连接,则 ______
,
而是的外角,
______出现矛盾,故假设不成立.
所以点在过,,三点的圆上.
同理可证点在内的情况.
【应用结论】
如图,四边形中,对角线,交于点,,平分.
若,求的度数.
若,,求线段的长.
23.本小题分
已知二次函数为常数图象的顶点横坐标比二次函数图象的顶点横坐标大.
求的值.
已知点在二次函数的图象上,点在二次函数的图象上.
若,求的最大值.
若,且时,始终有,求的值.
24.本小题分
如图,在正方形中,点,分别在边,上,,连接,交于点,过点,,的圆交于点,连接交于点.
证明:.
证明;
当时,求的值.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】解:把代入得,
解得,
二次函数解析式为,
,
二次函数图象的对称轴为直线;
该函数图象向上平移个单位长度后所得函数图象的解析式为,
平移后的二次函数图象与轴只有一个交点,
关于的一元二次方程有个相等的实数解,
,
解得,
即的值为.
18.【答案】解:,
理由:,,
,
,
∽.
注:答案不唯一,如选择;.
,
,
点为中点,
,
∽,
,
,
,
,
线段的长为.
19.【答案】
20.【答案】解:当时,,解得:,
二次函数的图象经过点,
二次函数;
二次函数图象的顶点在直线上;
理由:,
二次函数的顶点为,
当时,,
二次函数图象的顶点在直线上;
函数的图象如图所示:
的解集为:.
21.【答案】解:,点是中点,
,
由题可知,
,,
,,
解得,;
,
,
,
,
,
,
,
,
,
,
整理可得;
;
证明:连接,
,,
四边形是平行四边形,
,,
∽,
,
,
,
,
,
,
.
22.【答案】
23.【答案】解:函数,,
二次函数的顶点横坐标为,二次函数顶点横坐标为,
二次函数为常数图象的顶点横坐标比二次函数图象的顶点横坐标大,
,
;
点在二次函数的图象上,点在二次函数的图象上,
,,
,
,
,
时,有最大值;
,
,
,
,
,
整理得,,
即,
,,
时,始终有,
的值不会随的变化而变化,
.
24.【答案】证明:四边形是圆的内接四边形,
,
四边形是正方形,
,,
,
≌,,
,
,
≌,
,
,
,
;
证明:如图,
作,交于,
,∽,
,
由知,
,
,
,
;
解:如图,
延长,交于,作于,
,
四边形是正方形,
,,
,,
,
,
,
,
四边形是矩形,
,
,
∽,
,
,
,
,
,
,
不妨设,则,,
,
,
,
是圆的直径,
,
,
,
∽,
,
,
,
,
.
第1页,共1页
同课章节目录
