11.2与三角形有关的角课件(共28张PPT)
文档属性
| 名称 | 11.2与三角形有关的角课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-02 00:00:00 | ||
图片预览




文档简介
课件28张PPT。第十一章 三角形11.2 与三角形有关的角
第一课时 11.2.1 三角形的内角理解并会证明三角形内角和定理,能用三角形内角和定理解决实际问题。
掌握直角三角形的内角的性质,并会根据内角度数判断一个三角形是否为直角三角形。我们在小学时就学过:
三角形三个内角的和等于180°。
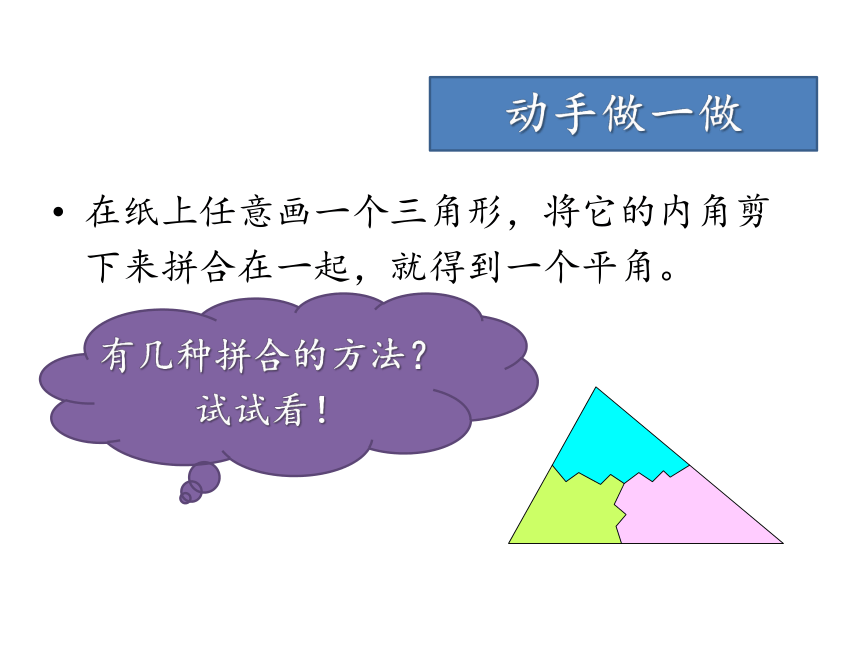
动脑想一想但是,这个结论对任意三角形都成立吗?该怎么去证明呢?为什么要证明它我们观察任意一个三角形,量出它的内角,都能得到这个结论,为什么还要证明呢?我们的观察都是有误差的!而且不同形状的三角形有无数个,我们验证不完这么多的三角形。只有经过令人信服的推理验证,才能完全让人信服。动手做一做在纸上任意画一个三角形,将它的内角剪下来拼合在一起,就得到一个平角。有几种拼合的方法?
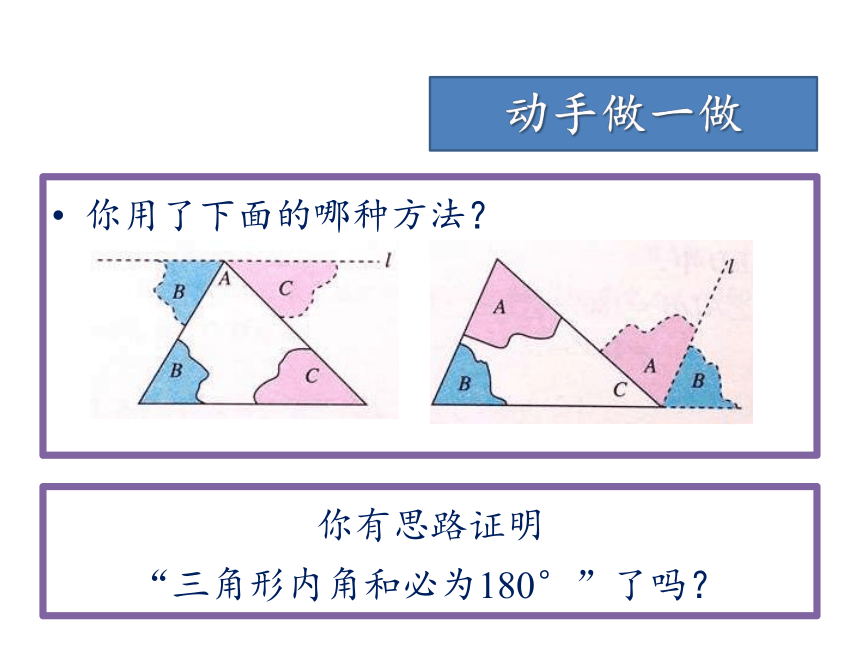
试试看!动手做一做你用了下面的哪种方法?
你有思路证明
“三角形内角和必为180°”了吗?方法:添辅助线为了证明的需要,在原来的图形上添画的线叫做辅助线。
做辅助线是几何证明过程中常用到的方法。辅助线通常画成虚线。
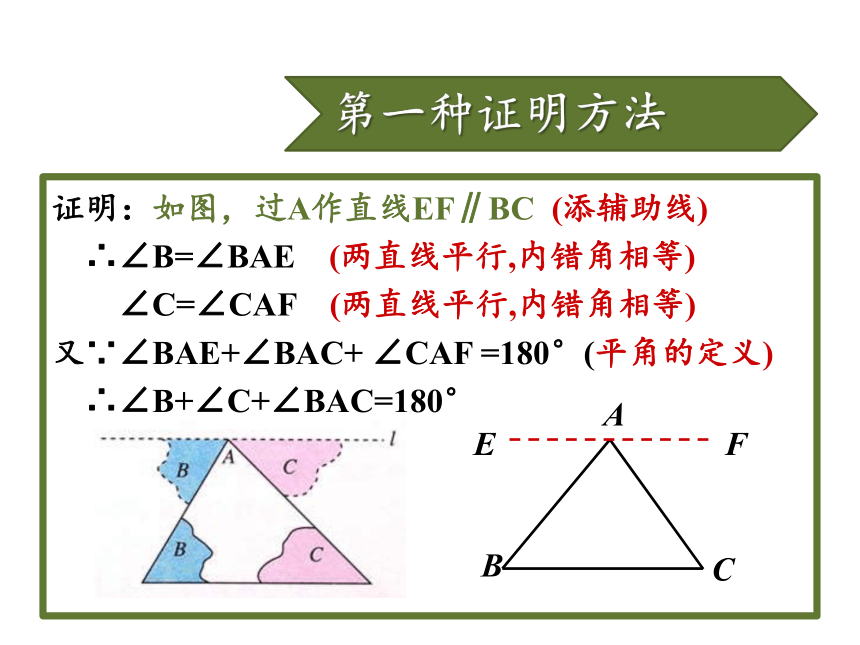
第一种证明方法证明:如图,过A作直线EF∥BC (添辅助线)
∴∠B=∠BAE (两直线平行,内错角相等)
∠C=∠CAF (两直线平行,内错角相等)
又∵∠BAE+∠BAC+ ∠CAF =180°(平角的定义)
∴∠B+∠C+∠BAC=180°
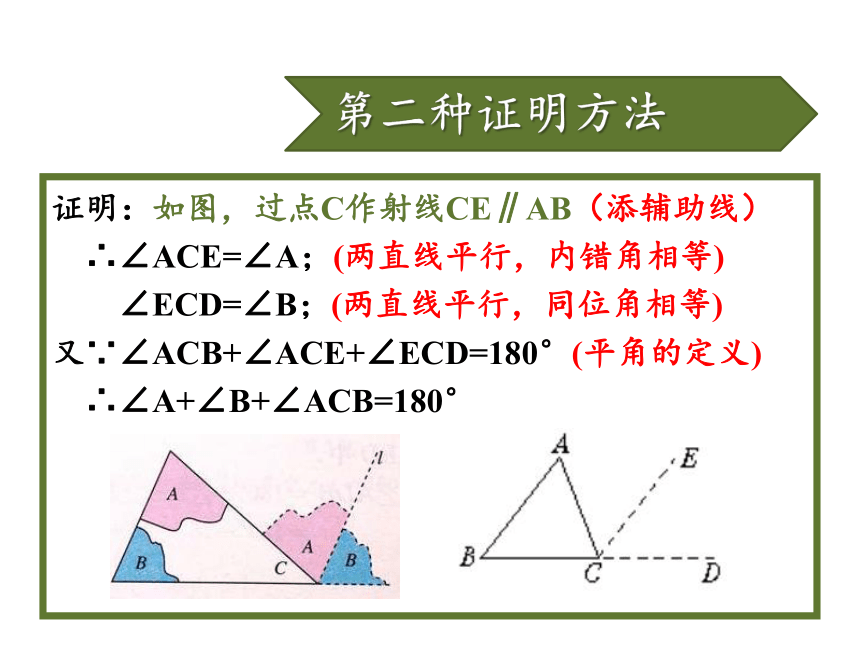
BCEFA第二种证明方法证明:如图,过点C作射线CE∥AB(添辅助线)
∴∠ACE=∠A;(两直线平行,内错角相等)
∠ECD=∠B;(两直线平行,同位角相等)
又∵∠ACB+∠ACE+∠ECD=180°(平角的定义)
∴∠A+∠B+∠ACB=180°三角形内角和定理经过刚才的证明,现在我们可以放心大胆地说:三角形三个内角的和等于180°在一个三角形中,已知两个内角的度数,就可以求出第三个内角的度数。如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度? 动脑想一想500800400解:
∵∠CAD=50°,∠DAB=80°
∴∠BAC=∠BAD-∠CAD=30°
∵AD//BE,∠DAB=80°
∴∠ABE=180°-∠DAB=100°
∵∠EBC=40°
∴∠ABC=60°
∴∠ACB=180°-∠ABC-∠BAC=90°
答:从C岛看A、B两岛的视角∠ACB是90°动脑想一想500800400直角三角形有一个角是直角的三角形叫做直角三角形。
直角三角形用符号“Rt△”表示,直角三角形ABC可以写成 Rt△ABC。已知在△ABC中,∠C=90°,那么∠A与∠B的和是多少?动脑想一想直角三角形的性质由三角形内角和定理,得到:
∠A+∠B+∠C=180°
∴∠A+∠B=180°-∠C=90°
直角三角形的两个内角互余现在我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余。动脑想一想反过来,有两个角互余的三角形是直角三角形吗?直角三角形的判定由三角形内角和定理,得到:
∠A+∠B+∠C=180°
又有∠A+∠B=90°
∴∠C=180°-(∠A+∠B)
=90°
有两个角互余的三角形是直角三角形直角三角形的性质和判定三角形是直角三角形三角形有两个内角互余学完本节课你应该知道三角形
的内角应用三角形内角和定理证明(两种方法)直角三角形直角三角形两锐角互余有两个内角互余的三角形是直角三角形动笔练一练在△ABC中,∠A=80°,∠B=∠C , 则∠C= 。
已知三角形三个内角的度数之比为1:3:5,则这三个内角的度数为 、 和 。
50°20°60°100°动笔练一练如图,∠C=∠D=90°,BC相交于点E。∠CAE和∠DBE有什么关系?为什么?动笔练一练
动笔练一练如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°。从C处观测A、B两处时视角∠ACB是多少?动笔练一练解:∵∠CBD= 45°
∴ ∠ABC=135°
∴ ∠ACB= 180°-∠A-∠ABC
= 180°- 45°- 135 °
= 15 °
动笔练一练三角形的三个内角中至少有 个是锐角,至多有 个是钝角。
三角形中最大的角不小于 。
260°1动笔练一练如图,在Rt△ABC中,∠ACB=90°,DE过点C且平行于AB。若∠BCE=35°,则∠A的度数是 。
55°课后练一练请同学们独立完成配套课后练习题下课!谢谢同学们!
第一课时 11.2.1 三角形的内角理解并会证明三角形内角和定理,能用三角形内角和定理解决实际问题。
掌握直角三角形的内角的性质,并会根据内角度数判断一个三角形是否为直角三角形。我们在小学时就学过:
三角形三个内角的和等于180°。
动脑想一想但是,这个结论对任意三角形都成立吗?该怎么去证明呢?为什么要证明它我们观察任意一个三角形,量出它的内角,都能得到这个结论,为什么还要证明呢?我们的观察都是有误差的!而且不同形状的三角形有无数个,我们验证不完这么多的三角形。只有经过令人信服的推理验证,才能完全让人信服。动手做一做在纸上任意画一个三角形,将它的内角剪下来拼合在一起,就得到一个平角。有几种拼合的方法?
试试看!动手做一做你用了下面的哪种方法?
你有思路证明
“三角形内角和必为180°”了吗?方法:添辅助线为了证明的需要,在原来的图形上添画的线叫做辅助线。
做辅助线是几何证明过程中常用到的方法。辅助线通常画成虚线。
第一种证明方法证明:如图,过A作直线EF∥BC (添辅助线)
∴∠B=∠BAE (两直线平行,内错角相等)
∠C=∠CAF (两直线平行,内错角相等)
又∵∠BAE+∠BAC+ ∠CAF =180°(平角的定义)
∴∠B+∠C+∠BAC=180°
BCEFA第二种证明方法证明:如图,过点C作射线CE∥AB(添辅助线)
∴∠ACE=∠A;(两直线平行,内错角相等)
∠ECD=∠B;(两直线平行,同位角相等)
又∵∠ACB+∠ACE+∠ECD=180°(平角的定义)
∴∠A+∠B+∠ACB=180°三角形内角和定理经过刚才的证明,现在我们可以放心大胆地说:三角形三个内角的和等于180°在一个三角形中,已知两个内角的度数,就可以求出第三个内角的度数。如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。从C岛看A、B两岛的视角∠ACB是多少度? 动脑想一想500800400解:
∵∠CAD=50°,∠DAB=80°
∴∠BAC=∠BAD-∠CAD=30°
∵AD//BE,∠DAB=80°
∴∠ABE=180°-∠DAB=100°
∵∠EBC=40°
∴∠ABC=60°
∴∠ACB=180°-∠ABC-∠BAC=90°
答:从C岛看A、B两岛的视角∠ACB是90°动脑想一想500800400直角三角形有一个角是直角的三角形叫做直角三角形。
直角三角形用符号“Rt△”表示,直角三角形ABC可以写成 Rt△ABC。已知在△ABC中,∠C=90°,那么∠A与∠B的和是多少?动脑想一想直角三角形的性质由三角形内角和定理,得到:
∠A+∠B+∠C=180°
∴∠A+∠B=180°-∠C=90°
直角三角形的两个内角互余现在我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余。动脑想一想反过来,有两个角互余的三角形是直角三角形吗?直角三角形的判定由三角形内角和定理,得到:
∠A+∠B+∠C=180°
又有∠A+∠B=90°
∴∠C=180°-(∠A+∠B)
=90°
有两个角互余的三角形是直角三角形直角三角形的性质和判定三角形是直角三角形三角形有两个内角互余学完本节课你应该知道三角形
的内角应用三角形内角和定理证明(两种方法)直角三角形直角三角形两锐角互余有两个内角互余的三角形是直角三角形动笔练一练在△ABC中,∠A=80°,∠B=∠C , 则∠C= 。
已知三角形三个内角的度数之比为1:3:5,则这三个内角的度数为 、 和 。
50°20°60°100°动笔练一练如图,∠C=∠D=90°,BC相交于点E。∠CAE和∠DBE有什么关系?为什么?动笔练一练
动笔练一练如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°。从C处观测A、B两处时视角∠ACB是多少?动笔练一练解:∵∠CBD= 45°
∴ ∠ABC=135°
∴ ∠ACB= 180°-∠A-∠ABC
= 180°- 45°- 135 °
= 15 °
动笔练一练三角形的三个内角中至少有 个是锐角,至多有 个是钝角。
三角形中最大的角不小于 。
260°1动笔练一练如图,在Rt△ABC中,∠ACB=90°,DE过点C且平行于AB。若∠BCE=35°,则∠A的度数是 。
55°课后练一练请同学们独立完成配套课后练习题下课!谢谢同学们!
