山东省济南市钢城区2024-2025学年七年级(上)期末数学试卷(五四学制)(含部分答案)
文档属性
| 名称 | 山东省济南市钢城区2024-2025学年七年级(上)期末数学试卷(五四学制)(含部分答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 510.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-15 15:28:57 | ||
图片预览




文档简介
山东省济南市钢城区2024-2025学年七年级(上)期末数学试卷(五四学制)
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数是无理数的是( )
A. B. C. D.
2.京剧是我国的国粹,下列京剧脸谱构成轴对称图形的是( )
A. B. C. D.
3.若长度是,,的三条线段能组成一个三角形,则的值可以是( )
A. B. C. D.
4.在平面直角坐标系中,点在轴上,则点在象限.
A. 一 B. 二 C. 三 D. 四
5.如图,≌,若,,则的度数为( )
A.
B.
C.
D.
6.在如图所示的正方形网格中,网格线的交点称为格点已知点,是格点,如果点也是图中的格点,且使得是以为腰的等腰直角三角形,则点的个数是( )
A.
B.
C.
D.
7.点,在函数的图象上,则、的大小关系是( )
A. B. C. D.
8.已知直线经过一、二,四象限,则直线的图象只能是图中的( )
A. B. C. D.
9.如图,在中,,,,以点为圆心,适当长为半径画弧,交、于、两点,分别以、为圆心,大于的长为半径画弧,两弧交于点,画射线交于点,长为( )
A. B. C. D.
10.如图,在平面直角坐标系中,对进行循环往复地轴对称变换,若原来点的坐标是,则经过第次变换后点的对应点的坐标为( )
A. B. C. D.
二、填空题:本题共5小题,每小题4分,共20分。
11.的相反数是______;的立方根为______.
12.将一次函数的图象沿轴向下平移个单位长度,则平移之后图象的函数表达式为______.
13.如图,在平面直角坐标系中,的顶点坐标分别是,,≌,若点在轴上,则点的坐标是______.
14.如图,在中,,于点,,分别是上的任意两点若的面积为,则图中阴影部分的面积为______.
15.勾股定理是数学中一颗璀璨的明珠,在人类的文明史上有杰出的贡献如图,在中,,,分别以的各边为一边向外部作正方形,把两个较小正方形按图放置,若图形的面积是,则图形的面积是______.
三、解答题:本题共10小题,共90分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
如图,等边中,是的中点,于,求的长.
17.本小题分
已知一个正数的两个不相等的平方根是与.
求这个正数;
求关于的方程的解.
18.本小题分
如图,已知中,,,,垂直平分,点为垂足,交于点,连接.
求的周长;
求的度数.
19.本小题分
某综合实践小组学习了“勾股定理”之后,设计方案测量风筝的垂直高度,测得水平距离的长为米;风筝线的长为米;牵线放风筝的小明的身高为米求风筝的垂直高度;
如果小明想风筝沿方向下降米,则他应该往回收线多少米?
20.本小题分
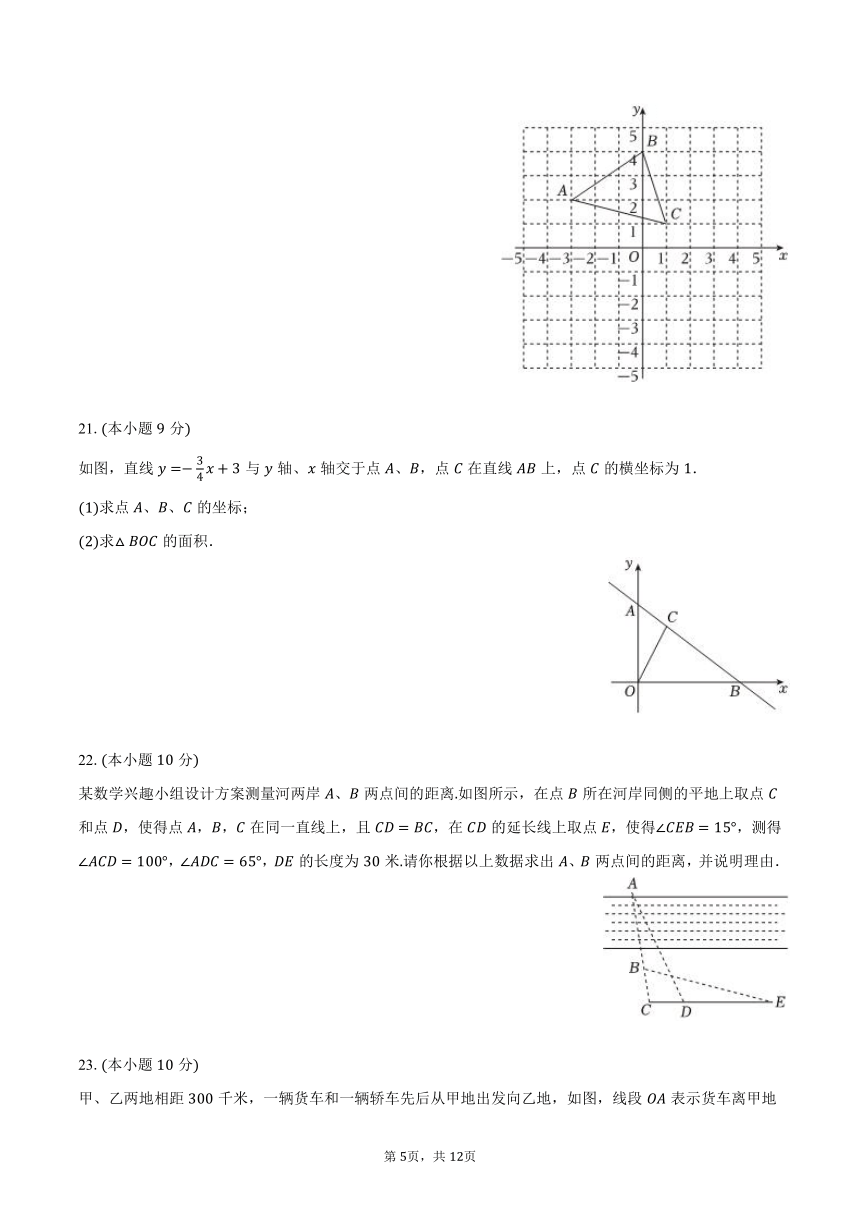
如图,在平面直角坐标系中,的三个顶点分别是,,.
画出关于轴对称的,的坐标为______;
在轴上画一点,使得的值最小并写出点的坐标.
21.本小题分
如图,直线与轴、轴交于点、,点在直线上,点的横坐标为.
求点、、的坐标;
求的面积.
22.本小题分
某数学兴趣小组设计方案测量河两岸、两点间的距离如图所示,在点所在河岸同侧的平地上取点和点,使得点,,在同一直线上,且,在的延长线上取点,使得,测得,,的长度为米请你根据以上数据求出、两点间的距离,并说明理由.
23.本小题分
甲、乙两地相距千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段表示货车离甲地距离千米与时间小时之间的函数关系,折线表示轿车离甲地距离千米与时间小时之间的函数关系,请根据图象解答下列问题:
求货车的平均速度?
轿车到达乙地时,货车距乙地多少千米?
若的解析式为:,则货车行驶多长时间轿车开始行驶?
轿车追上货车时,货车从甲地出发多少小时?
24.本小题分
我们把一只手掌,大拇指与小拇指尽量张开,两指间的距离称为指距根据最近人体构造学的研究成果表明,一般情况下人的身高和指距成某种关系数学综合与实践小组从函数角度进行了身高与指距的关系进行如下探究:
观察测量
数学综合与实践小组通过对我校师生抽样调查,收集数据,并抽取部分作为样本得到下表:
指距
身高
探究发现
小组建立如图所示的平面直角坐标系,横轴表示指距,纵轴表示身高,描出以表格中所有数据为坐标的各点.
经过观察思考,实践小组发现表格中有一组身高的数据有误,重新测量后证实了这一发现经过纠正,该组数据应为:指距为______时,身高约为______.
在平面直角坐标系中,描出这些数据对应的点,发现这些点大致位于同一个函数图象上,则这个函数最有可能是______填写函数类型
结论应用
应用上述发现的规律推测:
小婉的指距为,则她的身高约为______.
李老师的身高为,则他的指距约为______.
25.本小题分
【模型探究】如图,和中,,,且,连接,这一图形称“手拉手模型”求证≌,请你完善下列过程.
证明:,
.
即.
在和中
≌______
【模型指引】如图,中,,,以为端点引一条与腰相交的射线,在射线上取点,使,求的度数小亮同学通过观察,联想到手拉手模型,在上找一点,使,最后使问题得到解决请你帮他写出解答过程.
【拓展延伸】如图,中,,为任意角度,若射线不与腰相交,而是从端点向右下方延伸仍在射线上取点,使,试判断与有何数量关系?并写出简要说明.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】解:是等边三角形,
,,
是的中点,
,
,
,
.
17.【答案】解:由题意得,,
解得,
;
当时,,
,
.
18.【答案】解:垂直平分,
,
的周长
;
垂直平分,
,
,
,
;
;
19.【答案】解:由题意得:,米,
在中,由勾股定理得:米,
米;
如图,在上截取米,连接,
则米,
在中,由勾股定理得:米,
米,
他应该往回收线米.
20.【答案】
21.【答案】解:在一次函数中,
当时,;当时,,
,,
当时,,
;
.
22.【答案】解:,,
,
,
在与中,
,
≌,
,
又,
米,
答:、两点间的距离为米.
23.【答案】解:千米小时.
答:货车的平均速度为千米小时.
千米.
答:轿车到达乙地时,货车距乙地千米.
当时,得,
解得.
设货车从甲地出发小时轿车追上货车.
轿车在段的速度为千米小时,
根据图象,得,
解得.
答:货车从甲地出发小时轿车追上货车.
24.【答案】 一次函数
25.
第9页,共12页
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数是无理数的是( )
A. B. C. D.
2.京剧是我国的国粹,下列京剧脸谱构成轴对称图形的是( )
A. B. C. D.
3.若长度是,,的三条线段能组成一个三角形,则的值可以是( )
A. B. C. D.
4.在平面直角坐标系中,点在轴上,则点在象限.
A. 一 B. 二 C. 三 D. 四
5.如图,≌,若,,则的度数为( )
A.
B.
C.
D.
6.在如图所示的正方形网格中,网格线的交点称为格点已知点,是格点,如果点也是图中的格点,且使得是以为腰的等腰直角三角形,则点的个数是( )
A.
B.
C.
D.
7.点,在函数的图象上,则、的大小关系是( )
A. B. C. D.
8.已知直线经过一、二,四象限,则直线的图象只能是图中的( )
A. B. C. D.
9.如图,在中,,,,以点为圆心,适当长为半径画弧,交、于、两点,分别以、为圆心,大于的长为半径画弧,两弧交于点,画射线交于点,长为( )
A. B. C. D.
10.如图,在平面直角坐标系中,对进行循环往复地轴对称变换,若原来点的坐标是,则经过第次变换后点的对应点的坐标为( )
A. B. C. D.
二、填空题:本题共5小题,每小题4分,共20分。
11.的相反数是______;的立方根为______.
12.将一次函数的图象沿轴向下平移个单位长度,则平移之后图象的函数表达式为______.
13.如图,在平面直角坐标系中,的顶点坐标分别是,,≌,若点在轴上,则点的坐标是______.
14.如图,在中,,于点,,分别是上的任意两点若的面积为,则图中阴影部分的面积为______.
15.勾股定理是数学中一颗璀璨的明珠,在人类的文明史上有杰出的贡献如图,在中,,,分别以的各边为一边向外部作正方形,把两个较小正方形按图放置,若图形的面积是,则图形的面积是______.
三、解答题:本题共10小题,共90分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
如图,等边中,是的中点,于,求的长.
17.本小题分
已知一个正数的两个不相等的平方根是与.
求这个正数;
求关于的方程的解.
18.本小题分
如图,已知中,,,,垂直平分,点为垂足,交于点,连接.
求的周长;
求的度数.
19.本小题分
某综合实践小组学习了“勾股定理”之后,设计方案测量风筝的垂直高度,测得水平距离的长为米;风筝线的长为米;牵线放风筝的小明的身高为米求风筝的垂直高度;
如果小明想风筝沿方向下降米,则他应该往回收线多少米?
20.本小题分
如图,在平面直角坐标系中,的三个顶点分别是,,.
画出关于轴对称的,的坐标为______;
在轴上画一点,使得的值最小并写出点的坐标.
21.本小题分
如图,直线与轴、轴交于点、,点在直线上,点的横坐标为.
求点、、的坐标;
求的面积.
22.本小题分
某数学兴趣小组设计方案测量河两岸、两点间的距离如图所示,在点所在河岸同侧的平地上取点和点,使得点,,在同一直线上,且,在的延长线上取点,使得,测得,,的长度为米请你根据以上数据求出、两点间的距离,并说明理由.
23.本小题分
甲、乙两地相距千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段表示货车离甲地距离千米与时间小时之间的函数关系,折线表示轿车离甲地距离千米与时间小时之间的函数关系,请根据图象解答下列问题:
求货车的平均速度?
轿车到达乙地时,货车距乙地多少千米?
若的解析式为:,则货车行驶多长时间轿车开始行驶?
轿车追上货车时,货车从甲地出发多少小时?
24.本小题分
我们把一只手掌,大拇指与小拇指尽量张开,两指间的距离称为指距根据最近人体构造学的研究成果表明,一般情况下人的身高和指距成某种关系数学综合与实践小组从函数角度进行了身高与指距的关系进行如下探究:
观察测量
数学综合与实践小组通过对我校师生抽样调查,收集数据,并抽取部分作为样本得到下表:
指距
身高
探究发现
小组建立如图所示的平面直角坐标系,横轴表示指距,纵轴表示身高,描出以表格中所有数据为坐标的各点.
经过观察思考,实践小组发现表格中有一组身高的数据有误,重新测量后证实了这一发现经过纠正,该组数据应为:指距为______时,身高约为______.
在平面直角坐标系中,描出这些数据对应的点,发现这些点大致位于同一个函数图象上,则这个函数最有可能是______填写函数类型
结论应用
应用上述发现的规律推测:
小婉的指距为,则她的身高约为______.
李老师的身高为,则他的指距约为______.
25.本小题分
【模型探究】如图,和中,,,且,连接,这一图形称“手拉手模型”求证≌,请你完善下列过程.
证明:,
.
即.
在和中
≌______
【模型指引】如图,中,,,以为端点引一条与腰相交的射线,在射线上取点,使,求的度数小亮同学通过观察,联想到手拉手模型,在上找一点,使,最后使问题得到解决请你帮他写出解答过程.
【拓展延伸】如图,中,,为任意角度,若射线不与腰相交,而是从端点向右下方延伸仍在射线上取点,使,试判断与有何数量关系?并写出简要说明.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】解:是等边三角形,
,,
是的中点,
,
,
,
.
17.【答案】解:由题意得,,
解得,
;
当时,,
,
.
18.【答案】解:垂直平分,
,
的周长
;
垂直平分,
,
,
,
;
;
19.【答案】解:由题意得:,米,
在中,由勾股定理得:米,
米;
如图,在上截取米,连接,
则米,
在中,由勾股定理得:米,
米,
他应该往回收线米.
20.【答案】
21.【答案】解:在一次函数中,
当时,;当时,,
,,
当时,,
;
.
22.【答案】解:,,
,
,
在与中,
,
≌,
,
又,
米,
答:、两点间的距离为米.
23.【答案】解:千米小时.
答:货车的平均速度为千米小时.
千米.
答:轿车到达乙地时,货车距乙地千米.
当时,得,
解得.
设货车从甲地出发小时轿车追上货车.
轿车在段的速度为千米小时,
根据图象,得,
解得.
答:货车从甲地出发小时轿车追上货车.
24.【答案】 一次函数
25.
第9页,共12页
同课章节目录
