河北省平泉县第四中学数学(人教版)八年级上册:12.1 全等三角形 学案(无答案)
文档属性
| 名称 | 河北省平泉县第四中学数学(人教版)八年级上册:12.1 全等三角形 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 123.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-01 11:14:19 | ||
图片预览

文档简介
学习目标: 1、了解全等形、全等三角形的概念,明确全等三角形对应边、对应角相等。
2、在列举生活中常见的的全等图形的过程中,学会判断对应边、对应角的方法。
3、积极投入,激情展示,做最佳自己。
学习重点:全等三角形的性质及寻找全等三角形的对应边、对应角。
教学难点:寻找全等三角形的对应边、对应角。
教学过程:
一、温故知新
回忆:举出现实生活中能够完全重合的图形的例子 同一张底片洗出的同样大小照片是能够完全重合的(如图);
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
二、自主导学
1.全等形:能够完全重合的两个图形叫做 .
(1) 一个图形经过平移,翻折,旋转后,位置变化了,但 和 都没有改变,即平移,翻折,旋转前后的图形 是 。
(2) 如果两个图形全等,它们的形状大小一定都相同吗?全等形的特征是
2、全等三角形。能够完全重合的两个三角形叫做 (如下图)。
( http: / / www.21cnjy.com )
“全等”用符号“≌”来表示,读作“全等于”,如上图记作△ABC≌△A1B1C1
叫对应顶点,A←→A1,B←→B1,C←→C1
叫对应边,AB←→A1B1,AC←→ , ←→B1C1
叫对应角,∠A←→∠A1,∠B←→∠ ,∠C←→∠
注意:书写全等式时要求把对应顶点字母放在 的位置上。
3、全等三角形的性质。 全等三角形的 相等, 相等。
用符号表示为
∵△ABC≌△A1B1C1
∴ AB=A1B1, BC=B1C1, AC=A1C1
(全等三角形的 )
∴ ∠ A= ∠ A1, ∠ B= ∠B1 ,
∠ C= ∠C1(全等三角形的 )
三、合作探究
1、在找全等三角形的对应元素时一般有什么规律?
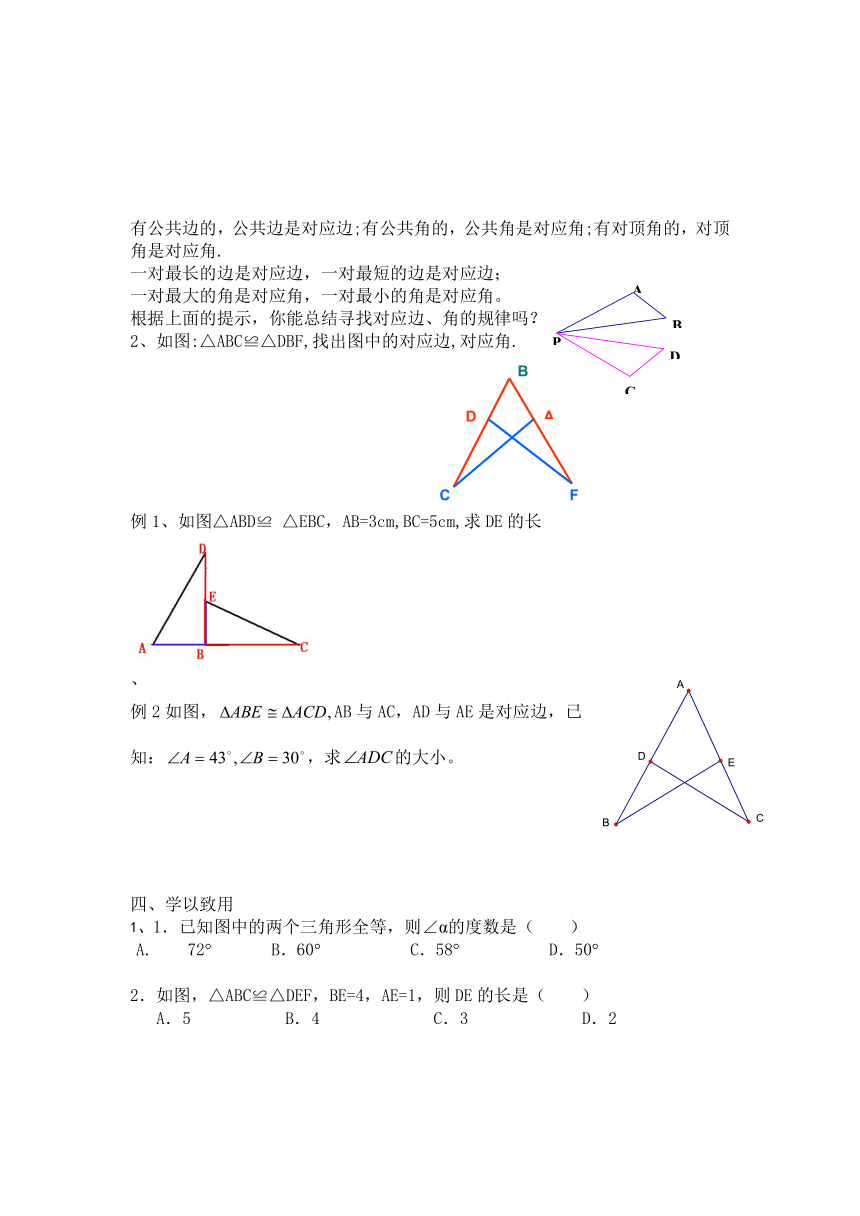
有公共边的,公共边是对应边;有公共角的,公共角是对应角;有对顶角的,对顶角是对应角.
一对最长的边是对应边,一对最短的边是对应边;
一对最大的角是对应角,一对最小的角是对应角。
根据上面的提示,你能总结寻找对应边、角的规律吗?
2、如图:△ABC≌△DBF,找出图中的对应边,对应角.
例1、如图△ABD≌ △EBC,AB=3cm,BC=5cm,求DE的长
( http: / / www.21cnjy.com )
、
例2如图,AB与AC,AD与AE是对应边,已知:,求的大小。
四、学以致用
1、1.已知图中的两个三角形全等,则∠α的度数是( )
A. 72° B. 60° C. 58° D. 50°
2.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是( )
A.5 B. 4 C. 3 D. 2
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
3.如图,△ ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A. 20° B. 30° C. 35° D. 40°
( http: / / www.21cnjy.com )
4. 下列说法中不正确的是( )
①全等三角形的对应边相等;②全等三角形的对应角相等;
③全等三角形的周长相等;④周长相等的两个三角形全等;
⑤全等三角形的面积相等;⑥面积相等的两个三角形全等.
A .④⑤ B. ④⑥ C. ③⑥ D. ③④⑤⑥
5.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是 _________ .
6.如图,若△ABC≌△A1B1C1,且∠A=110°,∠B=40°,则∠C1= ______度.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
7.已知:如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠AEB= _度.
五、自主作业
1、如图△ABC≌ △ADE,若∠D=∠B, ∠C= ∠AED,则∠DAE= ; ∠DAB= 。
( http: / / www.21cnjy.com )
2.如图所示,△BDC′是将长方形纸牌ABCD沿着BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形 _________ 对.
3、如图,△ABC≌△AED,AB是△ABC的最大边,
AE是△AED的最大边, ∠BAC 与∠ EAD对应角,且
∠BAC=25°, ∠B=35°,AB=3cm,BC=1cm,求出∠E,
∠ ADE的度数和线段DE,AE 的长度。∠BAD与
∠EAC相等吗?
A
B
C
D
A
B
C
D
C
D
A
B
E
P
A
B
D
C
B
D
A
C
F
第2题图
第1题图
第3题图
第5题图
第6题图
第7题图
2、在列举生活中常见的的全等图形的过程中,学会判断对应边、对应角的方法。
3、积极投入,激情展示,做最佳自己。
学习重点:全等三角形的性质及寻找全等三角形的对应边、对应角。
教学难点:寻找全等三角形的对应边、对应角。
教学过程:
一、温故知新
回忆:举出现实生活中能够完全重合的图形的例子 同一张底片洗出的同样大小照片是能够完全重合的(如图);
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
二、自主导学
1.全等形:能够完全重合的两个图形叫做 .
(1) 一个图形经过平移,翻折,旋转后,位置变化了,但 和 都没有改变,即平移,翻折,旋转前后的图形 是 。
(2) 如果两个图形全等,它们的形状大小一定都相同吗?全等形的特征是
2、全等三角形。能够完全重合的两个三角形叫做 (如下图)。
( http: / / www.21cnjy.com )
“全等”用符号“≌”来表示,读作“全等于”,如上图记作△ABC≌△A1B1C1
叫对应顶点,A←→A1,B←→B1,C←→C1
叫对应边,AB←→A1B1,AC←→ , ←→B1C1
叫对应角,∠A←→∠A1,∠B←→∠ ,∠C←→∠
注意:书写全等式时要求把对应顶点字母放在 的位置上。
3、全等三角形的性质。 全等三角形的 相等, 相等。
用符号表示为
∵△ABC≌△A1B1C1
∴ AB=A1B1, BC=B1C1, AC=A1C1
(全等三角形的 )
∴ ∠ A= ∠ A1, ∠ B= ∠B1 ,
∠ C= ∠C1(全等三角形的 )
三、合作探究
1、在找全等三角形的对应元素时一般有什么规律?
有公共边的,公共边是对应边;有公共角的,公共角是对应角;有对顶角的,对顶角是对应角.
一对最长的边是对应边,一对最短的边是对应边;
一对最大的角是对应角,一对最小的角是对应角。
根据上面的提示,你能总结寻找对应边、角的规律吗?
2、如图:△ABC≌△DBF,找出图中的对应边,对应角.
例1、如图△ABD≌ △EBC,AB=3cm,BC=5cm,求DE的长
( http: / / www.21cnjy.com )
、
例2如图,AB与AC,AD与AE是对应边,已知:,求的大小。
四、学以致用
1、1.已知图中的两个三角形全等,则∠α的度数是( )
A. 72° B. 60° C. 58° D. 50°
2.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是( )
A.5 B. 4 C. 3 D. 2
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
3.如图,△ ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A. 20° B. 30° C. 35° D. 40°
( http: / / www.21cnjy.com )
4. 下列说法中不正确的是( )
①全等三角形的对应边相等;②全等三角形的对应角相等;
③全等三角形的周长相等;④周长相等的两个三角形全等;
⑤全等三角形的面积相等;⑥面积相等的两个三角形全等.
A .④⑤ B. ④⑥ C. ③⑥ D. ③④⑤⑥
5.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是 _________ .
6.如图,若△ABC≌△A1B1C1,且∠A=110°,∠B=40°,则∠C1= ______度.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
7.已知:如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠AEB= _度.
五、自主作业
1、如图△ABC≌ △ADE,若∠D=∠B, ∠C= ∠AED,则∠DAE= ; ∠DAB= 。
( http: / / www.21cnjy.com )
2.如图所示,△BDC′是将长方形纸牌ABCD沿着BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形 _________ 对.
3、如图,△ABC≌△AED,AB是△ABC的最大边,
AE是△AED的最大边, ∠BAC 与∠ EAD对应角,且
∠BAC=25°, ∠B=35°,AB=3cm,BC=1cm,求出∠E,
∠ ADE的度数和线段DE,AE 的长度。∠BAD与
∠EAC相等吗?
A
B
C
D
A
B
C
D
C
D
A
B
E
P
A
B
D
C
B
D
A
C
F
第2题图
第1题图
第3题图
第5题图
第6题图
第7题图
