2.1数列的概念与简单表示法
图片预览










文档简介
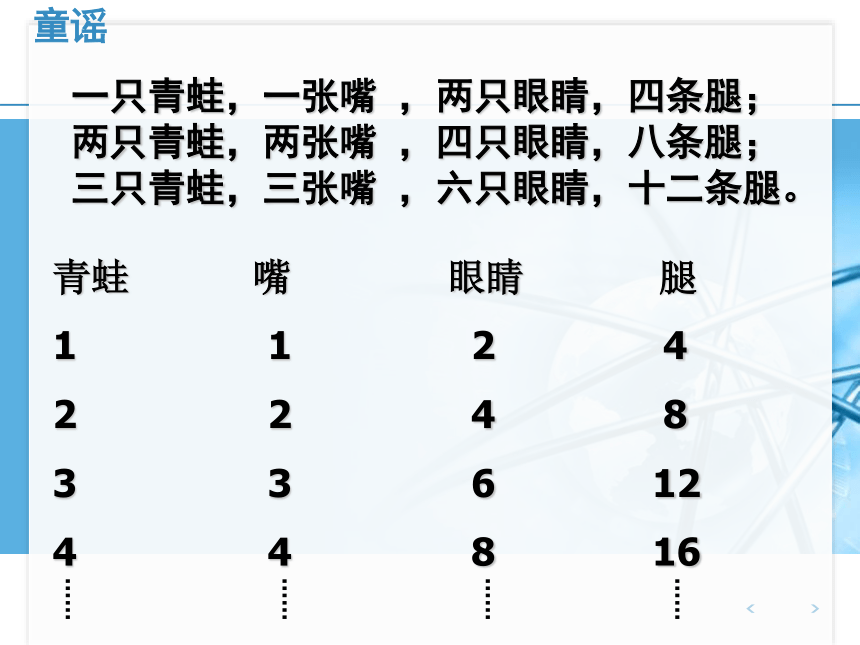
课件42张PPT。2.1 数列的概念与简单表示法童谣 一只青蛙,一张嘴 ,两只眼睛,四条腿;
两只青蛙,两张嘴 ,四只眼睛,八条腿;
三只青蛙,三张嘴 ,六只眼睛,十二条腿。青蛙 嘴 眼睛 腿
1 1 2 4
2 2 4 8
3 3 6 12
4 4 8 16 ……………………甲乙两位赌王打赌,约定如下:
(1)赌王甲第一天给赌王乙1元钱,第二天给3元,第三天给五元,第四天给7元,按照这个规律付下去。
(2)赌王乙第一天给赌王甲1分钱,第二天给2分,第三天给4分,第四天给8分,按照这个规律付下去。问题:你能写出付款规律吗?
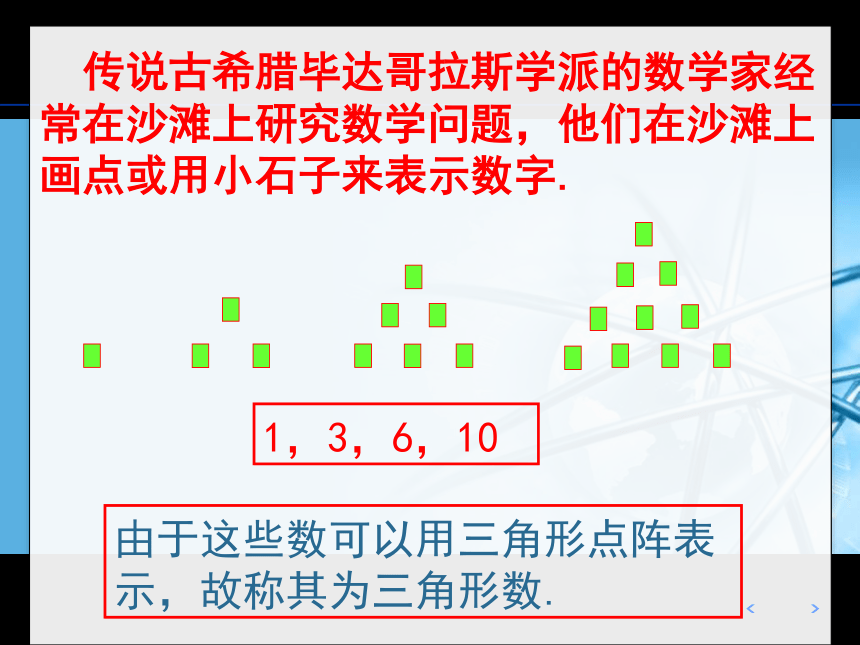
1,3,5,7,9,··· (1)单位:元 1,2,22,23,24 ··· (2)单位:分 两位赌王的付款数按顺序依次排列如下 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数字.由于这些数可以用三角形点阵表示,故称其为三角形数.1,3,6,10因为这些数能够表示成正方形,
故称为正方形数.1,4,9,16 1,1,2,3,5,8,13,……斐波那契 (Fibonacci;1170 ? 1250 ) 《算盘书》 1202.1、均是一列数,
2、有一定次序.观察上面4个例子它们有什么共同特点?特点:(1)1,3,6,10,… (2)1,2,4,8,16,…(4)2,4,8,16,32,…(3)1740,1823,1906,1989,…按照一定的次序排列的一列数叫做数列。 数列的定义数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项(首项),第2项,······,第n项, ······
1,3, 5, 7是一个数列,
7,5,3,1也是一个数列,
这两个数列是不是同一个数列呢?
不是。数列中的数是有先后次序的,两个数列即使所含的数完全相同,只要排列的次序不同,就是两个不同的数列。
-1,1,-1,1,-1,1.是不是一个数列呢?
数列中的数只要求按一定次序排列,并没有规定数列中的数必须不同,同一个数可以在数列中重复出现。[注 意] 数列与数集是两个不同的概念. 数集 中的元素具有无序性和互异性,而 数列中的数是按一定的次序排列的.
并且数列中可以有相同的数. 项数有限的数列叫做有穷数列,
项数无限的数列叫做无穷数列. 数列的分类1、根据数列项数是否有限分类:2、根据数列各项的变化趋势分类递增数列、递减数列、
摆动数列、常数数列. 从第2项起,每一项都大于它的
前一项的数列; 从第2项起,每一项都小于它的
前一项的数列; 从第2项起,有些项大于它的前
一项,有些项小于它的前一项的数列; 各项都相等的数列.递增数列:递减数列:摆动数列:常数列:其中右下标n表示项的位置序号数列的一般形式可以写成:2,4,8, 16,32 a4a1a2a3a5上面的数列又可简记为[注 意] {an}与an是两个不同的概念.
{an}表示数列a1,a2,a3,……而an表示的是数列{an}的第n项. 如何用数学式子表示递增数列、递减数列
和常数列?递增数列: 递减数列: 常数列: 问题(1)请你写出数列的第7项,第36项吗?
(2)32是该数列的项吗?
有何启迪?
在数列中,由项的序号就可以找到项;
由项就可以了解该项在数列中的位置,即知道该项的序号。
数列中的每一个项都对应着一个序号,反过来,每个序号也都对应着一个项。 对于数列中的每个序号n,都有唯一的一个数(项)an与之对应.项数n 1 2 3 4 …… 64
项an 1 2 22 23 …… 263
(自变量)(函数值)可以认为:数列与函数由此可见,序号与项构成了一个重要的关系其中自变量是序号;自变量的取值范围是正整数集(或它的有限子集{1,2,3,……,n})
在上面数列中,你能表示项an与项的序号n之间的关系吗? ——函数(数列是一种特殊的函数)。练习:课本31页 1 数列的项数n与项an之间的关系如果可以用一个公式表示,那么这个公式叫做这个数列的通项公式。数列通项公式如:数列 2, 4, 6, … …观察下列数列, 写出它们的通项公式:1.数列1,3,6,10,…的一个通项公式是( )B【解析】逐项验证,注意不能只验一至两项,要多验证几项.全优18页基础夯实1. 并不是所有的数列都有通项;2. 数列的通项可以有不同的形式;3. 数列的通项实际上就是相应函数 的解析式an= f(n), 但这是一类特 殊的函数.[注 意] 例 写出数列的一个通项公式,使它的前4项分别是下列各数:(1)1,3,5,7;解:此数列的前四项1,3,5,7都是序号的2倍减去1,所以通项公式是:(2) 解:此数列的前四项的分母都是序号加1,分子都是分母的平方减去1,所以通项公式是:(3) 解:此数列的前4项的值都等于序号与序号加上1的积的倒数,所以通项公式是: 解:此数列的绝对值都等于1,且奇数项为负,偶数项为正,所以通项公式是:(4)-1,1,-1, 1,-1, 1,-1(5) 解:此数列的前4项的绝对值都等于序号与序号加上1的积的倒数,且奇数项为负,偶数项为正,所以通项公式是: 写出下面数列的一个通项公式,使它的前4项分别是下列各数:练习:课本31页 4(1)(2)1.根据下面各数列的前几项,写出数列的一个通项公式.【解析】(1)原数列可写成∴数列的一个通项公式为全优17页变式训练1.根据下面各数列的前几项,写出数列的一个通项公式.【解析】全优17页变式训练(2)这是一个分数数列,分子是偶数列,而分母是1×3,3×5,5×7,7×9,9×11,…,为两个连续奇数的积,故所求数列的通项公式为1.根据下面各数列的前几项,写出数列的一个通项公式.【解析】全优17页变式训练 (3)∵各项的符号正负相间且绝对值呈分数形式,它的分子为奇数,分母为2的序号次幂,即可表示为1.根据下面各数列的前几项,写出数列的一个通项公式.【解析】全优17页变式训练(4)9,99,999,9 999,….(4)各项分别加上1,
变为10,100,1 000,10 000,…,∴an=10n-1.例2、图中的三角形称为谢宾斯基(Sierpinski)三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象。an
30
27
24
21
18
15
12
9
6
3
o 1 2 3 4 5 n数列用图象表示时,是一群孤立的点练习:课本33页 57.在数列{an}中,a1=2,a17=66,通项公式an是n的一次函数.
(1)求{an}的通项公式;【解析】(1)设an=kn+b,∴an=4n-2.(n∈N*).(2)88是否是数列{an}中的项?(2)令an=88,∴88不是{an}中的项.全优18页能力提升5.已知数列{an},an=an+m(a<0,n∈N*),满足a1=2,a2=4,则a3=________.2【解析】∴an=(-1)n+3,∴a3=(-1)3+3=2.全优18页基础夯实【例2】 已知数列{an}的通项为an=n2-5n+4,(2)n为何值时,an有最小值?并求此最小值.【解析】(2)∵an=n2-5n+4∵n∈N*,∴n=2或3时,an有最小值-2.全优17页典例剖析问题:如果一个数列{an}的首项a1=1,从第二项起每一项等于它的前一项的2倍再加1,
an = 2 an-1 + 1(n∈N,n>1)你能写出这个数列的前三项吗?像上述问题中给出数列的方法叫做递推法,其中an=2an-1+1(n>1)称为递推公式。递推公式也是数列的一种表示方法。 数列的第n项an与它前面相邻一项an-1
(或相邻几项)所满足的关系式叫递推公式;
给出数列的前几项(初始值)和递推公式
的数列叫递推数列。例3 设数列{an}满足 写出这个数列的前五项。练习:课本31页 22.数列1,3,6,10,15,…的递推公式是( )
A.an+1=an+n,n∈N*
B.an=an-1+n,n∈N*,n≥2
C.an+1=an+(n+1),n∈N*,n≥2
D.an=an-1+(n-1),n∈N*,n≥2B【解析】观察数列的变化规律:a2=a1+2,a3=a2+3,a4=a3+4,
a5=a4+5,…,归纳得出an=an-1+n(n∈N*,n≥2).全优69页限时规范训练
两只青蛙,两张嘴 ,四只眼睛,八条腿;
三只青蛙,三张嘴 ,六只眼睛,十二条腿。青蛙 嘴 眼睛 腿
1 1 2 4
2 2 4 8
3 3 6 12
4 4 8 16 ……………………甲乙两位赌王打赌,约定如下:
(1)赌王甲第一天给赌王乙1元钱,第二天给3元,第三天给五元,第四天给7元,按照这个规律付下去。
(2)赌王乙第一天给赌王甲1分钱,第二天给2分,第三天给4分,第四天给8分,按照这个规律付下去。问题:你能写出付款规律吗?
1,3,5,7,9,··· (1)单位:元 1,2,22,23,24 ··· (2)单位:分 两位赌王的付款数按顺序依次排列如下 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数字.由于这些数可以用三角形点阵表示,故称其为三角形数.1,3,6,10因为这些数能够表示成正方形,
故称为正方形数.1,4,9,16 1,1,2,3,5,8,13,……斐波那契 (Fibonacci;1170 ? 1250 ) 《算盘书》 1202.1、均是一列数,
2、有一定次序.观察上面4个例子它们有什么共同特点?特点:(1)1,3,6,10,… (2)1,2,4,8,16,…(4)2,4,8,16,32,…(3)1740,1823,1906,1989,…按照一定的次序排列的一列数叫做数列。 数列的定义数列中的每一个数叫做这个数列的项。各项依次叫做这个数列的第1项(首项),第2项,······,第n项, ······
1,3, 5, 7是一个数列,
7,5,3,1也是一个数列,
这两个数列是不是同一个数列呢?
不是。数列中的数是有先后次序的,两个数列即使所含的数完全相同,只要排列的次序不同,就是两个不同的数列。
-1,1,-1,1,-1,1.是不是一个数列呢?
数列中的数只要求按一定次序排列,并没有规定数列中的数必须不同,同一个数可以在数列中重复出现。[注 意] 数列与数集是两个不同的概念. 数集 中的元素具有无序性和互异性,而 数列中的数是按一定的次序排列的.
并且数列中可以有相同的数. 项数有限的数列叫做有穷数列,
项数无限的数列叫做无穷数列. 数列的分类1、根据数列项数是否有限分类:2、根据数列各项的变化趋势分类递增数列、递减数列、
摆动数列、常数数列. 从第2项起,每一项都大于它的
前一项的数列; 从第2项起,每一项都小于它的
前一项的数列; 从第2项起,有些项大于它的前
一项,有些项小于它的前一项的数列; 各项都相等的数列.递增数列:递减数列:摆动数列:常数列:其中右下标n表示项的位置序号数列的一般形式可以写成:2,4,8, 16,32 a4a1a2a3a5上面的数列又可简记为[注 意] {an}与an是两个不同的概念.
{an}表示数列a1,a2,a3,……而an表示的是数列{an}的第n项. 如何用数学式子表示递增数列、递减数列
和常数列?递增数列: 递减数列: 常数列: 问题(1)请你写出数列的第7项,第36项吗?
(2)32是该数列的项吗?
有何启迪?
在数列中,由项的序号就可以找到项;
由项就可以了解该项在数列中的位置,即知道该项的序号。
数列中的每一个项都对应着一个序号,反过来,每个序号也都对应着一个项。 对于数列中的每个序号n,都有唯一的一个数(项)an与之对应.项数n 1 2 3 4 …… 64
项an 1 2 22 23 …… 263
(自变量)(函数值)可以认为:数列与函数由此可见,序号与项构成了一个重要的关系其中自变量是序号;自变量的取值范围是正整数集(或它的有限子集{1,2,3,……,n})
在上面数列中,你能表示项an与项的序号n之间的关系吗? ——函数(数列是一种特殊的函数)。练习:课本31页 1 数列的项数n与项an之间的关系如果可以用一个公式表示,那么这个公式叫做这个数列的通项公式。数列通项公式如:数列 2, 4, 6, … …观察下列数列, 写出它们的通项公式:1.数列1,3,6,10,…的一个通项公式是( )B【解析】逐项验证,注意不能只验一至两项,要多验证几项.全优18页基础夯实1. 并不是所有的数列都有通项;2. 数列的通项可以有不同的形式;3. 数列的通项实际上就是相应函数 的解析式an= f(n), 但这是一类特 殊的函数.[注 意] 例 写出数列的一个通项公式,使它的前4项分别是下列各数:(1)1,3,5,7;解:此数列的前四项1,3,5,7都是序号的2倍减去1,所以通项公式是:(2) 解:此数列的前四项的分母都是序号加1,分子都是分母的平方减去1,所以通项公式是:(3) 解:此数列的前4项的值都等于序号与序号加上1的积的倒数,所以通项公式是: 解:此数列的绝对值都等于1,且奇数项为负,偶数项为正,所以通项公式是:(4)-1,1,-1, 1,-1, 1,-1(5) 解:此数列的前4项的绝对值都等于序号与序号加上1的积的倒数,且奇数项为负,偶数项为正,所以通项公式是: 写出下面数列的一个通项公式,使它的前4项分别是下列各数:练习:课本31页 4(1)(2)1.根据下面各数列的前几项,写出数列的一个通项公式.【解析】(1)原数列可写成∴数列的一个通项公式为全优17页变式训练1.根据下面各数列的前几项,写出数列的一个通项公式.【解析】全优17页变式训练(2)这是一个分数数列,分子是偶数列,而分母是1×3,3×5,5×7,7×9,9×11,…,为两个连续奇数的积,故所求数列的通项公式为1.根据下面各数列的前几项,写出数列的一个通项公式.【解析】全优17页变式训练 (3)∵各项的符号正负相间且绝对值呈分数形式,它的分子为奇数,分母为2的序号次幂,即可表示为1.根据下面各数列的前几项,写出数列的一个通项公式.【解析】全优17页变式训练(4)9,99,999,9 999,….(4)各项分别加上1,
变为10,100,1 000,10 000,…,∴an=10n-1.例2、图中的三角形称为谢宾斯基(Sierpinski)三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象。an
30
27
24
21
18
15
12
9
6
3
o 1 2 3 4 5 n数列用图象表示时,是一群孤立的点练习:课本33页 57.在数列{an}中,a1=2,a17=66,通项公式an是n的一次函数.
(1)求{an}的通项公式;【解析】(1)设an=kn+b,∴an=4n-2.(n∈N*).(2)88是否是数列{an}中的项?(2)令an=88,∴88不是{an}中的项.全优18页能力提升5.已知数列{an},an=an+m(a<0,n∈N*),满足a1=2,a2=4,则a3=________.2【解析】∴an=(-1)n+3,∴a3=(-1)3+3=2.全优18页基础夯实【例2】 已知数列{an}的通项为an=n2-5n+4,(2)n为何值时,an有最小值?并求此最小值.【解析】(2)∵an=n2-5n+4∵n∈N*,∴n=2或3时,an有最小值-2.全优17页典例剖析问题:如果一个数列{an}的首项a1=1,从第二项起每一项等于它的前一项的2倍再加1,
an = 2 an-1 + 1(n∈N,n>1)你能写出这个数列的前三项吗?像上述问题中给出数列的方法叫做递推法,其中an=2an-1+1(n>1)称为递推公式。递推公式也是数列的一种表示方法。 数列的第n项an与它前面相邻一项an-1
(或相邻几项)所满足的关系式叫递推公式;
给出数列的前几项(初始值)和递推公式
的数列叫递推数列。例3 设数列{an}满足 写出这个数列的前五项。练习:课本31页 22.数列1,3,6,10,15,…的递推公式是( )
A.an+1=an+n,n∈N*
B.an=an-1+n,n∈N*,n≥2
C.an+1=an+(n+1),n∈N*,n≥2
D.an=an-1+(n-1),n∈N*,n≥2B【解析】观察数列的变化规律:a2=a1+2,a3=a2+3,a4=a3+4,
a5=a4+5,…,归纳得出an=an-1+n(n∈N*,n≥2).全优69页限时规范训练
