沪教版七年级数学下册 17.1三角形的有关概念 练习(含详解)
文档属性
| 名称 | 沪教版七年级数学下册 17.1三角形的有关概念 练习(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 703.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-16 16:27:55 | ||
图片预览



文档简介
17.1三角形的有关概念
一、单选题
1.下列长度的三根木棒首尾相接,不能做成三角形框架的是( )
A.5cm 7cm 14cm B.7cm 9cm 13cm
C.5cm 7cm 10cm D.5cm 11cm 13cm
2.如图所示,一扇窗户打开后,用窗钩即可固定,这里所用的几何原理是( )
A.两点之间线段最短 B.垂线段最短
C.两定确定一条直线 D.三角形具有稳定性
3.下列分类正确的是( )
A.三角形可分为等腰三角形、等边三角形
B.三角形可分为不等边三角形、等腰三角形以及等边三角形
C.三角形可分为不等边三角形和等边三角形
D.三角形可分为不等边三角形和等腰三角形
4.下列各图中,正确画出中边上的高的是( )
A.① B.② C.③ D.④
5.下列说法中错误的是( )
A.三角形的高、中线、角平分线都是线段 B.三角形的三条中线交于同一点
C.三角形的三条角平分线交于同一点 D.直角三角形的三条高的交点在三角形内部
6.在长度分别为12厘米、10厘米、5厘米、4厘米的四条线段中,任选三条线段可以组成三角形的个数为( )
A.1个 B.2个 C.3个 D.4个
7.在中,线段,分别是高线,中线和角平分线,则( )
A. B. C. D.
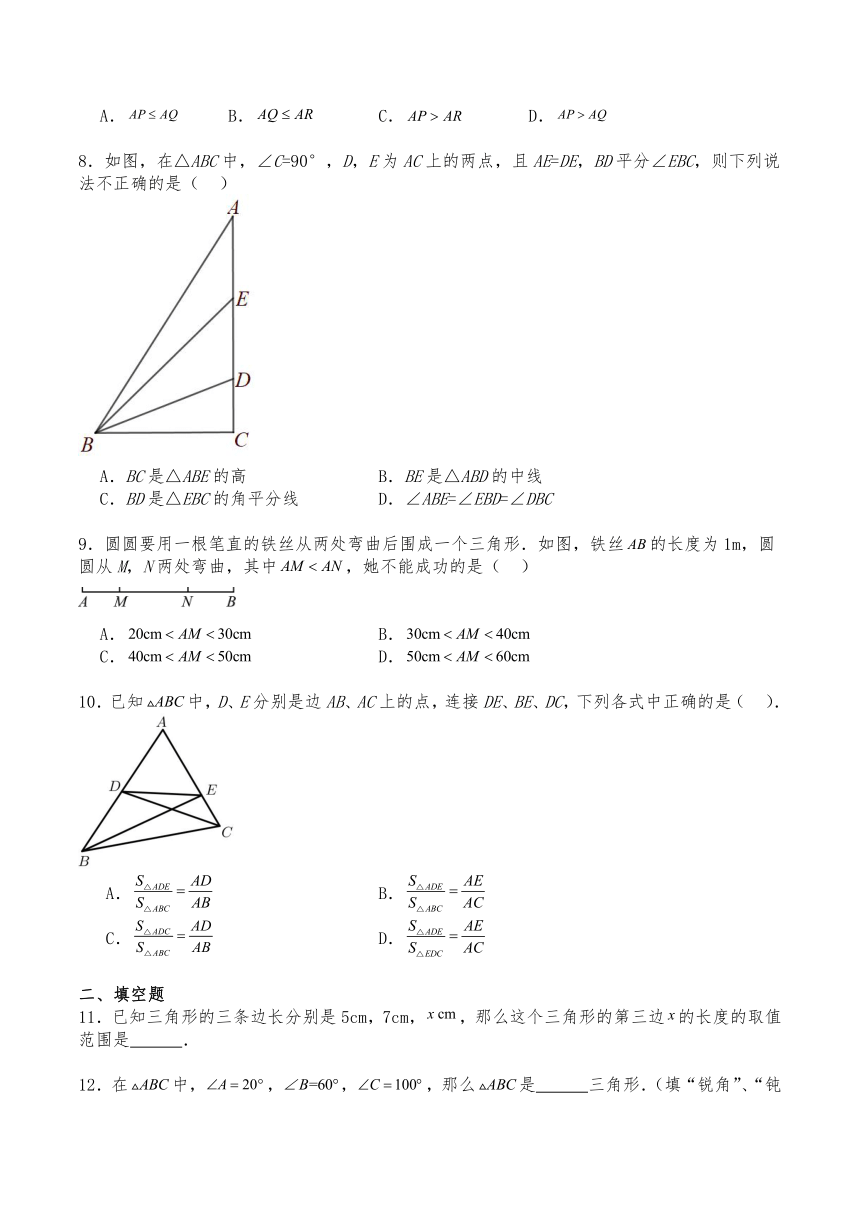
8.如图,在△ABC中,∠C=90°,D,E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
A.BC是△ABE的高 B.BE是△ABD的中线
C.BD是△EBC的角平分线 D.∠ABE=∠EBD=∠DBC
9.圆圆要用一根笔直的铁丝从两处弯曲后围成一个三角形.如图,铁丝的长度为1m,圆圆从M,N两处弯曲,其中,她不能成功的是( )
A. B.
C. D.
10.已知中,D、E分别是边AB、AC上的点,连接DE、BE、DC,下列各式中正确的是( ).
A. B.
C. D.
二、填空题
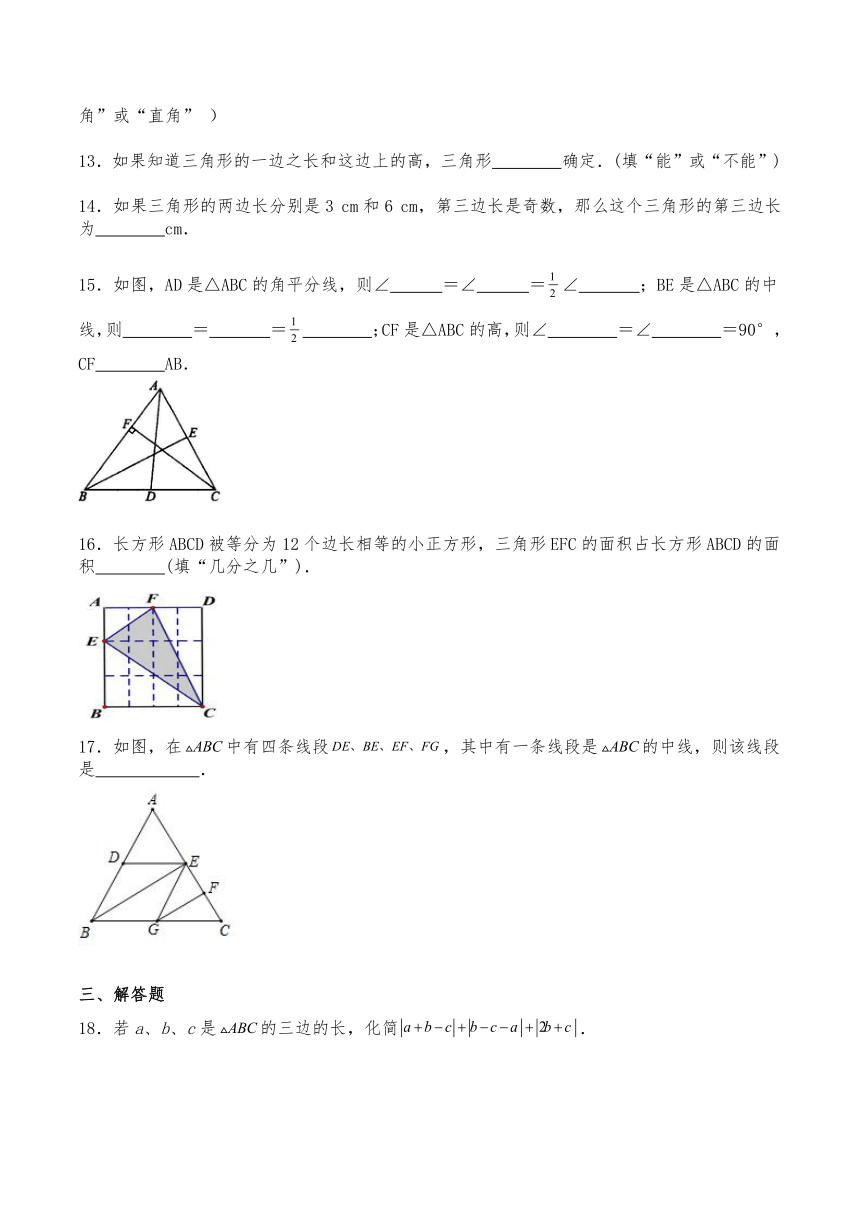
11.已知三角形的三条边长分别是5cm,7cm,,那么这个三角形的第三边的长度的取值范围是 .
12.在中,,,,那么是 三角形.(填“锐角”、“钝角”或“直角” )
13.如果知道三角形的一边之长和这边上的高,三角形 确定.(填“能”或“不能”)
14.如果三角形的两边长分别是3 cm和6 cm,第三边长是奇数,那么这个三角形的第三边长为 cm.
15.如图,AD是△ABC的角平分线,则∠ =∠ =∠ ;BE是△ABC的中线,则 = = ;CF是△ABC的高,则∠ =∠ =90°,CF AB.
16.长方形ABCD被等分为12个边长相等的小正方形,三角形EFC的面积占长方形ABCD的面积 (填“几分之几”).
17.如图,在中有四条线段,其中有一条线段是的中线,则该线段是 .
三、解答题
18.若a、b、c是的三边的长,化简.
19.在△ABC中,AB﹦9,BC﹦2,并且AC为奇数,那么△ABC的周长为多少?
20.根据要求作图并写好结论:
(1)画三角形,使得的长度等于厘米,,;
(2)在三角形中,作出的角平分线;
(3)在三角形中,作出边上中线.
21.如图,在中,是中线,是角平分线,是高,请完成以下填空:
(1)____________;
(2)____________;
(3)______;
(4)______.
22.如图,已知,AD、AE分别为△ABC的中线和高,AB=13,AC=5.
(1)△ABD和△ACD的周长相差多少?
(2)△ABD和△ACD的面积有什么关系,请说明理由.
23.已知,是的中线,是的中线,求.
24.已知:如图,是的角平分线,点E、F分别在、上,,平分.
(1)判断与的位置关系,并说明理由;
(2)若,,,且的面积为27,求的面积.
25.如图,有一块三角形菜地,若从顶点修一条小路交于点,小路正好将菜地分成面积相等的两部分.
(1)画出点的位置并说明理由.
(2)假设在菜地中有一点(如图所示),上是否存在点,使折线将三角形的面积分为面积相等的两部分.若存在,请画出点的位置.
答案
一、单选题
1.A
【分析】根据三角形的三边关系“两边之和大于第三边,两边之差小于第三边”进行分析判断.
【解析】解:,,不符合;
B,,符合;
C,,符合;
D,,符合.
故选:.
2.D
【分析】三角形具有稳定性,有着稳固、坚定、耐压的特点.
【解析】解:如图所示:可知点O、A、B构成了一个三角形,利用了三角形具有稳定性的特点.
选项A:错误;选项B:错误;选项C:错误;选项D:正确.
故选:D
3.D
【分析】根据三角形的分类即可求解.
【解析】解:三角形可分为不等边三角形和等腰三角形
故选:D.
4.D
【分析】根据三角形高的定义,过点B与边的垂线,且垂足在直线上,然后结合各选项图形解答.
【解析】解:根据三角形高线的定义,只有D选项中的是边上的高.
故选:D.
5.D
【分析】本题考查三角形的三条重要线段.根据中线,角平分线,高线的定义和性质,进行判断即可.
【解析】解:A、三角形的高、中线、角平分线都是线段,选项正确;
B、三角形的三条中线交于同一点,选项正确;
C、三角形的三条角平分线交于同一点,选项正确;
D、直角三角形的三条高的交点在直角顶点处,选项错误;
故选:D.
6.B
【分析】从4条线段里任取3条线段组合,分4种情况讨论,看哪种情况不符合三角形三边关系,舍去即可.
【解析】根据两边之和大于第三边才能组成三角形,可知能组成两个三角形,分别为:12厘米,10厘米,5厘米;12厘米,10厘米,4厘米.
故选:B
7.A
【分析】根据垂线段最短即可判断.本题考查三角形的角平分线、高、中线,垂线段最短等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【解析】解:∵是边上的高线,
∴根据垂线段最短可知:,
故选:A.
8.D
9.D
【分析】本题考查三角形的三边关系,根据“两边之和大于第三边,两边之差小于第三边”解答即可.
【解析】解:∵能构成三角形,
∴,
即,
∴,
∴选项D不符合要求,
故选D.
10.C
【分析】A选项,设点E、C到AB的距离分别为,,则,根据三角形面积公式进行判断即可;B选项设点D、B到AC的距离分别为x,y,则,,根据三角形面积公式进行判断即可;C选项,设点C到AB距离为h,,,根据三角形面积公式进行判断即可;D选项,设点D到AC距离为,则,,根据三角形面积公式进行判断即可
【解析】A选项:设点E、C到AB的距离分别为,,则,
,,
∴,故A错误;
B选项:设点D、B到AC的距离分别为x,y,则,,
,,,故B错误;
C选项:设点C到AB距离为h,,,
∴,故C正确;
D选项:设点D到AC距离为,则,,
∴,故D错误.
故选C.
二、填空题
11.
【分析】根据三角形的三边关系“三角形两边之和大于第三边,三角形两边之差小于第三边”进行解答即可得.
【解析】解:在三角形中,任意两边之和大于第三边,任意两边之差小于第三边,
,,
的取值范围是,
故答案为:.
12.钝角
【分析】根据三角形按角的分类可得结论.
【解析】解:在中,,,,
,
是钝角三角形,
故答案为:钝角.
13.不能
【分析】利用数形结合画图来判断知道三角形的一边之长和这边上的高是否能三角形.
【解析】画出简图比较容易判定.
解:如图,知道三角形的一边之长和这边上的高,三角形不能确定.
14.5 cm或7 cm;
【分析】可以构成三角形的三条线段必须满足两边和大于第三边,两边差小于第三边.
【解析】第三边长必须大于3cm小于9cm,又因为第三边长是奇数,所以第三边长可取5cm,或7cm.
15. BAD CAD BAC; AE CE AC; AFC CFB ⊥
【分析】分别根据三角形的角平分线、中线、高的定义填空即可.
【解析】AD是△ABC的角平分线,则∠=∠=∠;
BE是△ABC的中线,则;
CF是△ABC的高,则或=90°.
16.
【分析】利用长方形ABCD的面积分别减去直角三角形AEF、直角三角形CDF、直角三角形BCE的面积即可.
【解析】如图所示,长方形ABCD的面积=4×3=12,
直角三角形AEF面积=2×1÷2=1,
直角三角形BCE面积=2×4÷2=4,
直角三角形CDF面积=2×3÷2=3,
三角形EFC面积=12-1-4-3=4,
三角形EFC的面积占长方形ABCD的面积的:.
故答案为:.
17.
【分析】根据三角形一边的中点与此边所对顶点的连线叫做三角形的中线即可得出答案.
【解析】∵三角形的中线是一边的中点与此边所对顶点的连线
∴在中有四条线段中,线段BE是△ABC的中线
故答案为:BE
三、解答题
18.解:∵a、b、c是的三边,
∴,
∴,
∴
.
19.解:∵AB﹣BC<AC<AB﹢BC,(三角形三边关系)
∴9﹣2<AC<9﹢2,即7<AC<11
又A C为奇数,
∴A C﹦9
∴△ABC的周长﹦9+9+2﹦20
20.(1)如图,即为所求;
(2)如图,射线即为所求;
(3)如图,线段即为所求.
21.(1)解:是的中线,
,
故答案为:,;
(2)解:是中的角平分线,
,
故答案为:,;
(3)解:是中边的高,
,
,
故答案为:;
(4)解:,
,
故答案为:.
22.(1)△ABD的周长是AB、BD、AD三边的和
△ACD的周长是AC、CD、AD三边的和
因为AD为△ABC的中线
∴BD=DC
所以△ABD和△ACD的周长差就是AB与AC的差
故△ABD和△ACD的周长相差是8;
(2)因为AD为△ABC的中线
∴BD=DC
所以△ABD和△ACD是等底同高的三角形
故△ABD和△ACD的面积相等.
23.解:∵,是的中线,
∴,
∵是的中线,
∴.
24.(1)理由如下:
∵BD平分,平分,
.
,
,
,
.
(2),中上的高与中上高相同,
,
.
,中上的高与中上的高相同,
,
.
,中上的高与中上的高相同,
,
.
25.(1)如图,作BC得中点D,点即为所求;
理由:三角形的中线平分三角形的面积.
(2)作AB的中点D,连接,连接,作,交于点,连接,折线即为所求,
如图,折线即为所求,
理由:设交于点,
,
,
,
∴点D到AF的距离与点E到AF的距离相等,
,
,
折线平分的面积.
一、单选题
1.下列长度的三根木棒首尾相接,不能做成三角形框架的是( )
A.5cm 7cm 14cm B.7cm 9cm 13cm
C.5cm 7cm 10cm D.5cm 11cm 13cm
2.如图所示,一扇窗户打开后,用窗钩即可固定,这里所用的几何原理是( )
A.两点之间线段最短 B.垂线段最短
C.两定确定一条直线 D.三角形具有稳定性
3.下列分类正确的是( )
A.三角形可分为等腰三角形、等边三角形
B.三角形可分为不等边三角形、等腰三角形以及等边三角形
C.三角形可分为不等边三角形和等边三角形
D.三角形可分为不等边三角形和等腰三角形
4.下列各图中,正确画出中边上的高的是( )
A.① B.② C.③ D.④
5.下列说法中错误的是( )
A.三角形的高、中线、角平分线都是线段 B.三角形的三条中线交于同一点
C.三角形的三条角平分线交于同一点 D.直角三角形的三条高的交点在三角形内部
6.在长度分别为12厘米、10厘米、5厘米、4厘米的四条线段中,任选三条线段可以组成三角形的个数为( )
A.1个 B.2个 C.3个 D.4个
7.在中,线段,分别是高线,中线和角平分线,则( )
A. B. C. D.
8.如图,在△ABC中,∠C=90°,D,E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
A.BC是△ABE的高 B.BE是△ABD的中线
C.BD是△EBC的角平分线 D.∠ABE=∠EBD=∠DBC
9.圆圆要用一根笔直的铁丝从两处弯曲后围成一个三角形.如图,铁丝的长度为1m,圆圆从M,N两处弯曲,其中,她不能成功的是( )
A. B.
C. D.
10.已知中,D、E分别是边AB、AC上的点,连接DE、BE、DC,下列各式中正确的是( ).
A. B.
C. D.
二、填空题
11.已知三角形的三条边长分别是5cm,7cm,,那么这个三角形的第三边的长度的取值范围是 .
12.在中,,,,那么是 三角形.(填“锐角”、“钝角”或“直角” )
13.如果知道三角形的一边之长和这边上的高,三角形 确定.(填“能”或“不能”)
14.如果三角形的两边长分别是3 cm和6 cm,第三边长是奇数,那么这个三角形的第三边长为 cm.
15.如图,AD是△ABC的角平分线,则∠ =∠ =∠ ;BE是△ABC的中线,则 = = ;CF是△ABC的高,则∠ =∠ =90°,CF AB.
16.长方形ABCD被等分为12个边长相等的小正方形,三角形EFC的面积占长方形ABCD的面积 (填“几分之几”).
17.如图,在中有四条线段,其中有一条线段是的中线,则该线段是 .
三、解答题
18.若a、b、c是的三边的长,化简.
19.在△ABC中,AB﹦9,BC﹦2,并且AC为奇数,那么△ABC的周长为多少?
20.根据要求作图并写好结论:
(1)画三角形,使得的长度等于厘米,,;
(2)在三角形中,作出的角平分线;
(3)在三角形中,作出边上中线.
21.如图,在中,是中线,是角平分线,是高,请完成以下填空:
(1)____________;
(2)____________;
(3)______;
(4)______.
22.如图,已知,AD、AE分别为△ABC的中线和高,AB=13,AC=5.
(1)△ABD和△ACD的周长相差多少?
(2)△ABD和△ACD的面积有什么关系,请说明理由.
23.已知,是的中线,是的中线,求.
24.已知:如图,是的角平分线,点E、F分别在、上,,平分.
(1)判断与的位置关系,并说明理由;
(2)若,,,且的面积为27,求的面积.
25.如图,有一块三角形菜地,若从顶点修一条小路交于点,小路正好将菜地分成面积相等的两部分.
(1)画出点的位置并说明理由.
(2)假设在菜地中有一点(如图所示),上是否存在点,使折线将三角形的面积分为面积相等的两部分.若存在,请画出点的位置.
答案
一、单选题
1.A
【分析】根据三角形的三边关系“两边之和大于第三边,两边之差小于第三边”进行分析判断.
【解析】解:,,不符合;
B,,符合;
C,,符合;
D,,符合.
故选:.
2.D
【分析】三角形具有稳定性,有着稳固、坚定、耐压的特点.
【解析】解:如图所示:可知点O、A、B构成了一个三角形,利用了三角形具有稳定性的特点.
选项A:错误;选项B:错误;选项C:错误;选项D:正确.
故选:D
3.D
【分析】根据三角形的分类即可求解.
【解析】解:三角形可分为不等边三角形和等腰三角形
故选:D.
4.D
【分析】根据三角形高的定义,过点B与边的垂线,且垂足在直线上,然后结合各选项图形解答.
【解析】解:根据三角形高线的定义,只有D选项中的是边上的高.
故选:D.
5.D
【分析】本题考查三角形的三条重要线段.根据中线,角平分线,高线的定义和性质,进行判断即可.
【解析】解:A、三角形的高、中线、角平分线都是线段,选项正确;
B、三角形的三条中线交于同一点,选项正确;
C、三角形的三条角平分线交于同一点,选项正确;
D、直角三角形的三条高的交点在直角顶点处,选项错误;
故选:D.
6.B
【分析】从4条线段里任取3条线段组合,分4种情况讨论,看哪种情况不符合三角形三边关系,舍去即可.
【解析】根据两边之和大于第三边才能组成三角形,可知能组成两个三角形,分别为:12厘米,10厘米,5厘米;12厘米,10厘米,4厘米.
故选:B
7.A
【分析】根据垂线段最短即可判断.本题考查三角形的角平分线、高、中线,垂线段最短等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【解析】解:∵是边上的高线,
∴根据垂线段最短可知:,
故选:A.
8.D
9.D
【分析】本题考查三角形的三边关系,根据“两边之和大于第三边,两边之差小于第三边”解答即可.
【解析】解:∵能构成三角形,
∴,
即,
∴,
∴选项D不符合要求,
故选D.
10.C
【分析】A选项,设点E、C到AB的距离分别为,,则,根据三角形面积公式进行判断即可;B选项设点D、B到AC的距离分别为x,y,则,,根据三角形面积公式进行判断即可;C选项,设点C到AB距离为h,,,根据三角形面积公式进行判断即可;D选项,设点D到AC距离为,则,,根据三角形面积公式进行判断即可
【解析】A选项:设点E、C到AB的距离分别为,,则,
,,
∴,故A错误;
B选项:设点D、B到AC的距离分别为x,y,则,,
,,,故B错误;
C选项:设点C到AB距离为h,,,
∴,故C正确;
D选项:设点D到AC距离为,则,,
∴,故D错误.
故选C.
二、填空题
11.
【分析】根据三角形的三边关系“三角形两边之和大于第三边,三角形两边之差小于第三边”进行解答即可得.
【解析】解:在三角形中,任意两边之和大于第三边,任意两边之差小于第三边,
,,
的取值范围是,
故答案为:.
12.钝角
【分析】根据三角形按角的分类可得结论.
【解析】解:在中,,,,
,
是钝角三角形,
故答案为:钝角.
13.不能
【分析】利用数形结合画图来判断知道三角形的一边之长和这边上的高是否能三角形.
【解析】画出简图比较容易判定.
解:如图,知道三角形的一边之长和这边上的高,三角形不能确定.
14.5 cm或7 cm;
【分析】可以构成三角形的三条线段必须满足两边和大于第三边,两边差小于第三边.
【解析】第三边长必须大于3cm小于9cm,又因为第三边长是奇数,所以第三边长可取5cm,或7cm.
15. BAD CAD BAC; AE CE AC; AFC CFB ⊥
【分析】分别根据三角形的角平分线、中线、高的定义填空即可.
【解析】AD是△ABC的角平分线,则∠=∠=∠;
BE是△ABC的中线,则;
CF是△ABC的高,则或=90°.
16.
【分析】利用长方形ABCD的面积分别减去直角三角形AEF、直角三角形CDF、直角三角形BCE的面积即可.
【解析】如图所示,长方形ABCD的面积=4×3=12,
直角三角形AEF面积=2×1÷2=1,
直角三角形BCE面积=2×4÷2=4,
直角三角形CDF面积=2×3÷2=3,
三角形EFC面积=12-1-4-3=4,
三角形EFC的面积占长方形ABCD的面积的:.
故答案为:.
17.
【分析】根据三角形一边的中点与此边所对顶点的连线叫做三角形的中线即可得出答案.
【解析】∵三角形的中线是一边的中点与此边所对顶点的连线
∴在中有四条线段中,线段BE是△ABC的中线
故答案为:BE
三、解答题
18.解:∵a、b、c是的三边,
∴,
∴,
∴
.
19.解:∵AB﹣BC<AC<AB﹢BC,(三角形三边关系)
∴9﹣2<AC<9﹢2,即7<AC<11
又A C为奇数,
∴A C﹦9
∴△ABC的周长﹦9+9+2﹦20
20.(1)如图,即为所求;
(2)如图,射线即为所求;
(3)如图,线段即为所求.
21.(1)解:是的中线,
,
故答案为:,;
(2)解:是中的角平分线,
,
故答案为:,;
(3)解:是中边的高,
,
,
故答案为:;
(4)解:,
,
故答案为:.
22.(1)△ABD的周长是AB、BD、AD三边的和
△ACD的周长是AC、CD、AD三边的和
因为AD为△ABC的中线
∴BD=DC
所以△ABD和△ACD的周长差就是AB与AC的差
故△ABD和△ACD的周长相差是8;
(2)因为AD为△ABC的中线
∴BD=DC
所以△ABD和△ACD是等底同高的三角形
故△ABD和△ACD的面积相等.
23.解:∵,是的中线,
∴,
∵是的中线,
∴.
24.(1)理由如下:
∵BD平分,平分,
.
,
,
,
.
(2),中上的高与中上高相同,
,
.
,中上的高与中上的高相同,
,
.
,中上的高与中上的高相同,
,
.
25.(1)如图,作BC得中点D,点即为所求;
理由:三角形的中线平分三角形的面积.
(2)作AB的中点D,连接,连接,作,交于点,连接,折线即为所求,
如图,折线即为所求,
理由:设交于点,
,
,
,
∴点D到AF的距离与点E到AF的距离相等,
,
,
折线平分的面积.
同课章节目录
