沪教版七年级数学下册试题 17.3全等三角形的概念与性质 (含答案)
文档属性
| 名称 | 沪教版七年级数学下册试题 17.3全等三角形的概念与性质 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 621.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-16 10:54:21 | ||
图片预览



文档简介
17.3全等三角形的概念与性质
一、单选题
1.下列两个图形是全等图形的是( )
A.两张同底版的照片 B.周长相等的两个长方形
C.面积相等的两个正方形 D.面积相等的两个三角形
2.下列说法:①两个形状相同的图形称为全等图形;②边、角分别对应相等的两个多边形全等;③全等图形的形状、大小都相同;④面积相等的两个三角形全等.其中正确的是( )
A.①②③ B.①②④ C.①③ D.②③
3.说法中正确的是( )
A.全等三角形是指形状相同的两个三角形 B.全等三角形是指面积相等的两个三角形
C.两个等边三角形是全等三角形 D.周长相等的两个三角形不一定全等
4.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
5.已知图中的两个三角形全等,AD与CE是对应边,则A的对应角是( )
A. B. C. D.
6.如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是( )
A.6cm B.5cm C.7cm D.无法确定
7.已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18cm2,则EF边上的高是( )
A.6cm B.7cm C.8cm D.9cm
8.如图,ABC≌DCB,若AC=7,BE﹦5,则DE的长为( )
A.2 B.3 C.4 D.5
9.如图,若则下列结论中不成立的是( )
A.
B.
C.DA平分
D.
10.如图,,点B和点C是对应顶点,,记,当时,与之间的数量关系为( )
A. B. C. D.
二、填空题
11.把两个全等的三角形重合到一起,重合的顶点叫做 ,重合的边叫做 ,重合的角叫做 .记两个三角形全等时,通常把表示 的字母写在对应位置上.
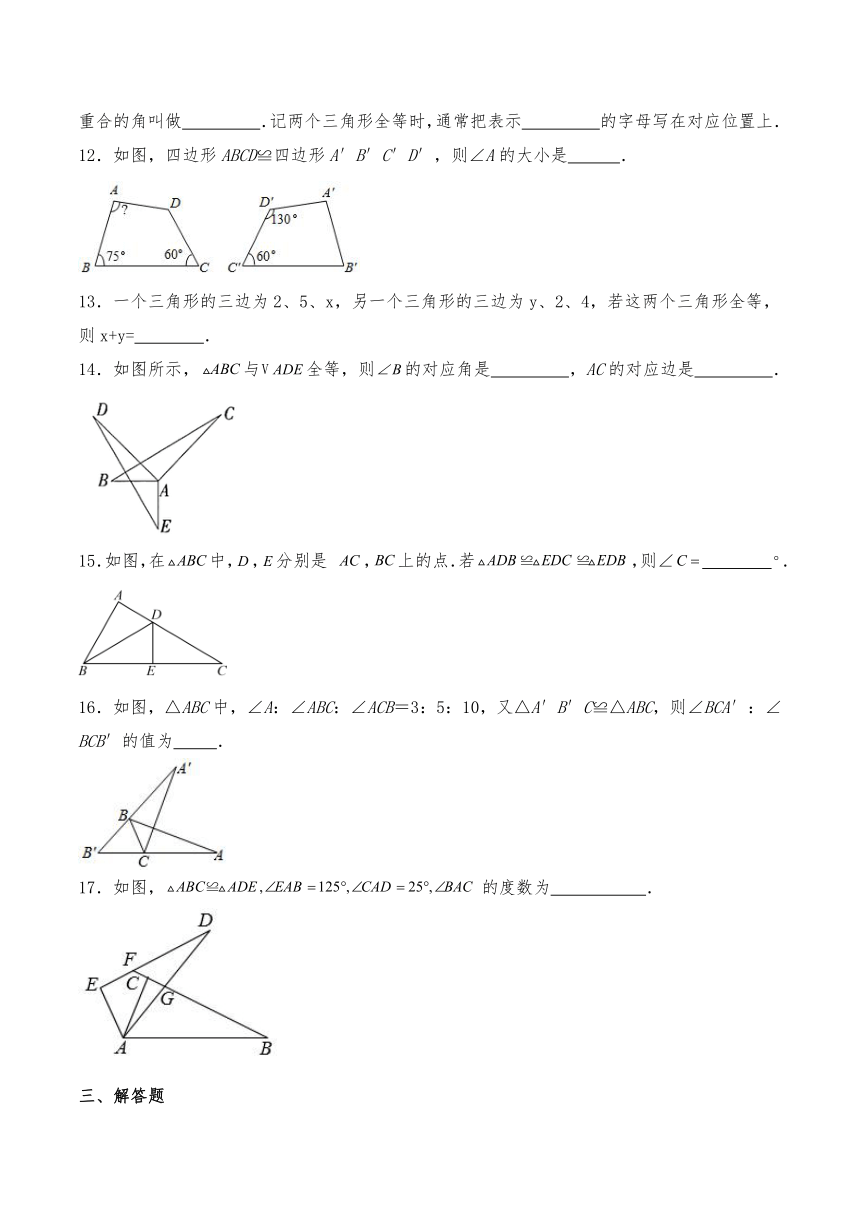
12.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是 .
13.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、4,若这两个三角形全等,则x+y= .
14.如图所示,与全等,则的对应角是 ,AC的对应边是 .
15.如图,在中,,分别是 ,上的点.若,则∠ .
16.如图,△ABC中,∠A:∠ABC:∠ACB=3:5:10,又△A′B′C≌△ABC,则∠BCA′:∠BCB′的值为 .
17.如图,的度数为 .
三、解答题
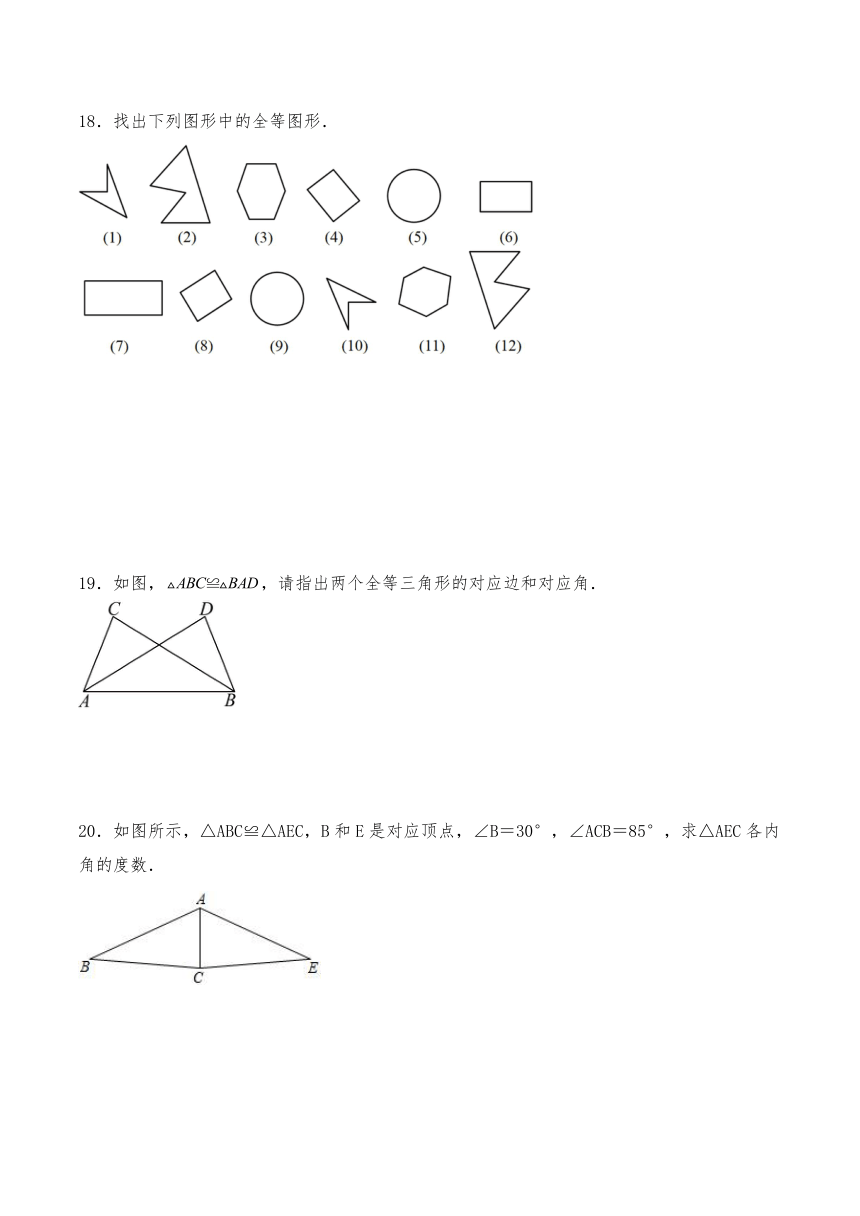
18.找出下列图形中的全等图形.
19.如图,,请指出两个全等三角形的对应边和对应角.
20.如图所示,△ABC≌△AEC,B和E是对应顶点,∠B=30°,∠ACB=85°,求△AEC各内角的度数.
21.如图,,,,求的度数.
22.如图19,△ACF≌△ADE,AD=9,AE=4,求DF的长.
23.如图所示,已知,点B,D,E,C在同一条直线上.
(1)与有何关系?请说明理由.
(2)与相等吗?请说明理由.
24.如图,,且点D在上,求证:.
25.如图所示,已知,.
(1)求的度数;
(2)求的度数.
26.如图所示,点D,A,E在一条直线上,,,,求:
(1)的度数;
(2)的度数.
27.如图,A,D,E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE.
28.如图所示,,,,交于点E,.
(1)求的度数.
(2)试判断与的位置关系,并说明理由.
答案
一、单选题
1.C
【分析】根据全等图形的定义,对各个选项逐个分析,即可得到答案.
【解析】∵两张同底版的照片,照片的尺寸可以是不一样的
∴两张同底版的照片不一定是全等图形,故选项A错误;
∵周长相等的两个长方形,分成的长和宽可以不相等
∴周长相等的两个长方形不一定是全等图形,故选项B错误;
∵两个正方形面积相等,且正方形的四条边长度相同
∴面积相等的两个正方形是全等图形,故选项C正确;
∵面积相等的两个三角形,对应的底边长和三角形的高可以不同
∴面积相等的两个三角形不一定是全等图形,故选项D错误;
故选:C.
2.D
【分析】根据全等形的概念:能够完全重合的两个图形叫做全等形进行分析即可.
【解析】①两个形状相同的图形称为全等图形,说法错误;
②边、角分别对应相等的两个多边形全等,说法正确;
③全等图形的形状、大小都相同,说法正确;
④面积相等的两个三角形是全等图形,说法错误,
故答案为:D.
3.D
【分析】本题主要考查了全等三角形的概念,根据能够完全重合的两个三角形是全等三角形,对各选项分析判断后利用排除法求解.
【解析】解:形状相同的两个三角形若其大小不相等就不是全等三角形,故选项A错误;
面积相等的两个三角形形状不一定相同,不一定是全等三角形,故选项B错误;
两个等边三角形,形状相同,边长不一定相等,不一定能完全重合,不一定是全等三角形,故选项C错误.
长相等的两个三角形不一定全等,故选项D正确;
故选D.
4.A
【分析】根据∠α是b、c边的夹角,然后写出即可.
【解析】解:∵两个三角形全等,
∴∠α的度数是72°.
故选:A.
5.A
【分析】观察图形,AD与CE是对应边,根据对应边去找对应角.
【解析】观察图形知,AD与CE是对应边
∴∠B与∠ACD是对应角
又∠D与∠E是对应角
∴∠A与∠BCE是对应角.
故选:A.
6.C
【分析】根据全等三角形的性质计算即可;
【解析】∵△ABC≌△ADE,
∴,
∵BC=7cm,
∴;
故答案选C.
7.A
【分析】利用全等三角形的性质找出同一个三角形的底边长及面积,代入面积公式即可求解三角形的高.
【解析】解:设△DEF的面积为s,边EF上的高为h,
∵△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18平方厘米,
∴两三角形的面积相等,即s=18,即有,
解得:h=6,
即EF边上的高为6cm,
故选:A.
8.A
【分析】由题意易得AC=DB=7,然后问题可求解.
【解析】解:∵ABC≌DCB,AC=7,
∴AC=DB=7,
∵BE﹦5,
∴DE=DB-BE=2,
故选A.
9.D
【分析】根据全等三角形的性质得出∠B=∠ADE,∠BAC=∠DAE,AB=AD,∠E=∠C,再逐个判断即可.
【解析】解:A.∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC ∠DAC=∠DAE ∠DAC,
∴∠BAD=∠CAE,故本选项不符合题意;
B.如图,∵△ABC≌△ADE,
∴∠C=∠E,
∵∠AOE=∠DOC,∠E+∠CAE+∠AOE=180°,∠C+∠COD+∠CDE=180°,
∴∠CAE=∠CDE,
∵∠BAD=∠CAE,
∴∠BAD=∠CDE,故本选项不符合题意;
C.∵△ABC≌△ADE,
∴∠B=∠ADE,AB=AD,
∴∠B=∠BDA,
∴∠BDA=∠ADE,
∴AD平分∠BDE,故本选项不符合题意;
D.∵△ABC≌△ADE,
∴BC=DE,故本选项符合题意;
故选:D.
10.B
【分析】根据全等三角形对应边相等可得AB=AC,全等三角形对应角相等可得∠BAO=∠CAD,然后求出∠BAC=α,再根据等腰三角形两底角相等求出∠ABC,然后根据两直线平行,同旁内角互补表示出∠OBC,整理即可.
【解析】∵,
∴,
∴,
在中,
∵,
∴,
∵,
∴,
∴,整理得,
故选:B.
二、填空题
11. 对应顶点 对应边 对应角 对应顶点
【分析】根据能够完全重合的两个图形叫做全等形,以及对应顶点、对应边、对应角的概念填空.
【解析】解:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.记两个三角形全等时,通常把表示对应顶点的字母写在对应位置上.
故答案为:对应顶点;对应边;对应角;对应顶点.
12.95°
【分析】根据两个多边形全等,则对应角相等,利用四边形内角和为360°即可求解.
【解析】∵四边形ABCD≌四边形A′B′C′D′
∴∠D=∠D′=130゜
∵四边形ABCD的内角和为360゜
∴∠A=360゜-∠B-∠C-∠D=95゜
故答案为:95゜
13.9
【分析】根据全等三角形对应边相等求出x、y的值,然后相加即可得解.
【解析】解:∵两个三角形全等,
∴x=4,y=5,
∴x+y=4+5=9.
故答案为9.
14. ∠E AD
【解析】首先确定三角形的对应顶点,再将对应顶点放在对应位置写出两个三角形的全等关系,即,然后按照对应关系即可写出对应边和对应角,的对应角为,AC的对应边为AD.
答案:∠E AD
15.
【分析】本题考查了全等三角形的性质及三角形内角和定理,根据全等三角形的性质及三角形内角和定理可得,即可求得.
【解析】解:∵,
∴,,
又∵,
∴,
∴,
∵,
∴,
∴,
故答案为:.
16.1:4
【分析】根据题意可先求出∠ACB的度数,然后根据全等的性质分别求出∠BCA′,∠BCB′的值即可得出结论.
【解析】解:∵∠A:∠ABC:∠ACB=3:5:10,
∴∠ACB=180°×=100°,
∵△A′B′C≌△ABC,
∴∠A′CB′=∠ACB=100°,
∴∠BCB′=180°﹣∠ACB=180°﹣100°=80°,
∠BCA′=∠ACB﹣∠A′CB′=100°﹣80°=20°,
∴∠BCA′:∠BCB′=20°:80°=1:4.
故答案为:1:4.
17.
【分析】根据全等三角形的性质求出∠EAD=∠CAB,求出∠DAB=∠EAC =50°,即可得到∠BAC的度数.
【解析】解:∵ABC≌ADE,
∴∠EAD=∠CAB,
∴∠EAD﹣∠CAD=∠CAB﹣∠CAD,
∴∠EAC=∠DAB,
∵∠EAB=125°,∠CAD=25°,
∴∠DAB=∠EAC=(125°﹣25°)=50°,
∴∠BAC=50°+25°=75°.
故答案为:75°.
三、解答题
18.解:由题意得:(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形.
19.解:∵,
∴对应边:与,与,与;对应角:与,与,与.
20.解:∵△ABC≌△AEC,∴∠B=∠E=30°,∠ACB=∠ACE=85°,
∴∠EAC=65°.
21.解:方法一 ∵,
∴,
∴.
方法二 ∵,,
∴,
∴,
∴.
22.解:∵△ACF≌△ADE,
∴AF=AE,
∴DF=AD-AF=AD-AE=9-4=5.
23.(1)解:.理由如下:
∵,
∴.
∵,,
∴.
(2).理由如下:
∵,
∴.
∵,,
∴.
24.证明:∵,
∴.
∵,
∴.
25.(1)解:设,,,
∵
∴,
解得.
.
∵,
∴;
(2)解:由(1)知,.
,
.
.
26.(1)解:,
,
,即.
点,,在一条直线上,
,
∴.
(2)解:由三角形外角的性质,得,
∴.
27.解:(1)∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE;
(2)△ABD满足∠ADB=90°时,BD∥CE,
理由是:∵△BAD≌△ACE,
∴∠E=∠ADB=90°,
∴∠BDE=180° 90°=90°=∠E,
∴BD∥CE.
28.(1)解:,
.
.
.
(2)解:,理由如下:
,
.
,
.
.
.
一、单选题
1.下列两个图形是全等图形的是( )
A.两张同底版的照片 B.周长相等的两个长方形
C.面积相等的两个正方形 D.面积相等的两个三角形
2.下列说法:①两个形状相同的图形称为全等图形;②边、角分别对应相等的两个多边形全等;③全等图形的形状、大小都相同;④面积相等的两个三角形全等.其中正确的是( )
A.①②③ B.①②④ C.①③ D.②③
3.说法中正确的是( )
A.全等三角形是指形状相同的两个三角形 B.全等三角形是指面积相等的两个三角形
C.两个等边三角形是全等三角形 D.周长相等的两个三角形不一定全等
4.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
5.已知图中的两个三角形全等,AD与CE是对应边,则A的对应角是( )
A. B. C. D.
6.如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是( )
A.6cm B.5cm C.7cm D.无法确定
7.已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18cm2,则EF边上的高是( )
A.6cm B.7cm C.8cm D.9cm
8.如图,ABC≌DCB,若AC=7,BE﹦5,则DE的长为( )
A.2 B.3 C.4 D.5
9.如图,若则下列结论中不成立的是( )
A.
B.
C.DA平分
D.
10.如图,,点B和点C是对应顶点,,记,当时,与之间的数量关系为( )
A. B. C. D.
二、填空题
11.把两个全等的三角形重合到一起,重合的顶点叫做 ,重合的边叫做 ,重合的角叫做 .记两个三角形全等时,通常把表示 的字母写在对应位置上.
12.如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是 .
13.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、4,若这两个三角形全等,则x+y= .
14.如图所示,与全等,则的对应角是 ,AC的对应边是 .
15.如图,在中,,分别是 ,上的点.若,则∠ .
16.如图,△ABC中,∠A:∠ABC:∠ACB=3:5:10,又△A′B′C≌△ABC,则∠BCA′:∠BCB′的值为 .
17.如图,的度数为 .
三、解答题
18.找出下列图形中的全等图形.
19.如图,,请指出两个全等三角形的对应边和对应角.
20.如图所示,△ABC≌△AEC,B和E是对应顶点,∠B=30°,∠ACB=85°,求△AEC各内角的度数.
21.如图,,,,求的度数.
22.如图19,△ACF≌△ADE,AD=9,AE=4,求DF的长.
23.如图所示,已知,点B,D,E,C在同一条直线上.
(1)与有何关系?请说明理由.
(2)与相等吗?请说明理由.
24.如图,,且点D在上,求证:.
25.如图所示,已知,.
(1)求的度数;
(2)求的度数.
26.如图所示,点D,A,E在一条直线上,,,,求:
(1)的度数;
(2)的度数.
27.如图,A,D,E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE.
28.如图所示,,,,交于点E,.
(1)求的度数.
(2)试判断与的位置关系,并说明理由.
答案
一、单选题
1.C
【分析】根据全等图形的定义,对各个选项逐个分析,即可得到答案.
【解析】∵两张同底版的照片,照片的尺寸可以是不一样的
∴两张同底版的照片不一定是全等图形,故选项A错误;
∵周长相等的两个长方形,分成的长和宽可以不相等
∴周长相等的两个长方形不一定是全等图形,故选项B错误;
∵两个正方形面积相等,且正方形的四条边长度相同
∴面积相等的两个正方形是全等图形,故选项C正确;
∵面积相等的两个三角形,对应的底边长和三角形的高可以不同
∴面积相等的两个三角形不一定是全等图形,故选项D错误;
故选:C.
2.D
【分析】根据全等形的概念:能够完全重合的两个图形叫做全等形进行分析即可.
【解析】①两个形状相同的图形称为全等图形,说法错误;
②边、角分别对应相等的两个多边形全等,说法正确;
③全等图形的形状、大小都相同,说法正确;
④面积相等的两个三角形是全等图形,说法错误,
故答案为:D.
3.D
【分析】本题主要考查了全等三角形的概念,根据能够完全重合的两个三角形是全等三角形,对各选项分析判断后利用排除法求解.
【解析】解:形状相同的两个三角形若其大小不相等就不是全等三角形,故选项A错误;
面积相等的两个三角形形状不一定相同,不一定是全等三角形,故选项B错误;
两个等边三角形,形状相同,边长不一定相等,不一定能完全重合,不一定是全等三角形,故选项C错误.
长相等的两个三角形不一定全等,故选项D正确;
故选D.
4.A
【分析】根据∠α是b、c边的夹角,然后写出即可.
【解析】解:∵两个三角形全等,
∴∠α的度数是72°.
故选:A.
5.A
【分析】观察图形,AD与CE是对应边,根据对应边去找对应角.
【解析】观察图形知,AD与CE是对应边
∴∠B与∠ACD是对应角
又∠D与∠E是对应角
∴∠A与∠BCE是对应角.
故选:A.
6.C
【分析】根据全等三角形的性质计算即可;
【解析】∵△ABC≌△ADE,
∴,
∵BC=7cm,
∴;
故答案选C.
7.A
【分析】利用全等三角形的性质找出同一个三角形的底边长及面积,代入面积公式即可求解三角形的高.
【解析】解:设△DEF的面积为s,边EF上的高为h,
∵△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18平方厘米,
∴两三角形的面积相等,即s=18,即有,
解得:h=6,
即EF边上的高为6cm,
故选:A.
8.A
【分析】由题意易得AC=DB=7,然后问题可求解.
【解析】解:∵ABC≌DCB,AC=7,
∴AC=DB=7,
∵BE﹦5,
∴DE=DB-BE=2,
故选A.
9.D
【分析】根据全等三角形的性质得出∠B=∠ADE,∠BAC=∠DAE,AB=AD,∠E=∠C,再逐个判断即可.
【解析】解:A.∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC ∠DAC=∠DAE ∠DAC,
∴∠BAD=∠CAE,故本选项不符合题意;
B.如图,∵△ABC≌△ADE,
∴∠C=∠E,
∵∠AOE=∠DOC,∠E+∠CAE+∠AOE=180°,∠C+∠COD+∠CDE=180°,
∴∠CAE=∠CDE,
∵∠BAD=∠CAE,
∴∠BAD=∠CDE,故本选项不符合题意;
C.∵△ABC≌△ADE,
∴∠B=∠ADE,AB=AD,
∴∠B=∠BDA,
∴∠BDA=∠ADE,
∴AD平分∠BDE,故本选项不符合题意;
D.∵△ABC≌△ADE,
∴BC=DE,故本选项符合题意;
故选:D.
10.B
【分析】根据全等三角形对应边相等可得AB=AC,全等三角形对应角相等可得∠BAO=∠CAD,然后求出∠BAC=α,再根据等腰三角形两底角相等求出∠ABC,然后根据两直线平行,同旁内角互补表示出∠OBC,整理即可.
【解析】∵,
∴,
∴,
在中,
∵,
∴,
∵,
∴,
∴,整理得,
故选:B.
二、填空题
11. 对应顶点 对应边 对应角 对应顶点
【分析】根据能够完全重合的两个图形叫做全等形,以及对应顶点、对应边、对应角的概念填空.
【解析】解:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.记两个三角形全等时,通常把表示对应顶点的字母写在对应位置上.
故答案为:对应顶点;对应边;对应角;对应顶点.
12.95°
【分析】根据两个多边形全等,则对应角相等,利用四边形内角和为360°即可求解.
【解析】∵四边形ABCD≌四边形A′B′C′D′
∴∠D=∠D′=130゜
∵四边形ABCD的内角和为360゜
∴∠A=360゜-∠B-∠C-∠D=95゜
故答案为:95゜
13.9
【分析】根据全等三角形对应边相等求出x、y的值,然后相加即可得解.
【解析】解:∵两个三角形全等,
∴x=4,y=5,
∴x+y=4+5=9.
故答案为9.
14. ∠E AD
【解析】首先确定三角形的对应顶点,再将对应顶点放在对应位置写出两个三角形的全等关系,即,然后按照对应关系即可写出对应边和对应角,的对应角为,AC的对应边为AD.
答案:∠E AD
15.
【分析】本题考查了全等三角形的性质及三角形内角和定理,根据全等三角形的性质及三角形内角和定理可得,即可求得.
【解析】解:∵,
∴,,
又∵,
∴,
∴,
∵,
∴,
∴,
故答案为:.
16.1:4
【分析】根据题意可先求出∠ACB的度数,然后根据全等的性质分别求出∠BCA′,∠BCB′的值即可得出结论.
【解析】解:∵∠A:∠ABC:∠ACB=3:5:10,
∴∠ACB=180°×=100°,
∵△A′B′C≌△ABC,
∴∠A′CB′=∠ACB=100°,
∴∠BCB′=180°﹣∠ACB=180°﹣100°=80°,
∠BCA′=∠ACB﹣∠A′CB′=100°﹣80°=20°,
∴∠BCA′:∠BCB′=20°:80°=1:4.
故答案为:1:4.
17.
【分析】根据全等三角形的性质求出∠EAD=∠CAB,求出∠DAB=∠EAC =50°,即可得到∠BAC的度数.
【解析】解:∵ABC≌ADE,
∴∠EAD=∠CAB,
∴∠EAD﹣∠CAD=∠CAB﹣∠CAD,
∴∠EAC=∠DAB,
∵∠EAB=125°,∠CAD=25°,
∴∠DAB=∠EAC=(125°﹣25°)=50°,
∴∠BAC=50°+25°=75°.
故答案为:75°.
三、解答题
18.解:由题意得:(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形.
19.解:∵,
∴对应边:与,与,与;对应角:与,与,与.
20.解:∵△ABC≌△AEC,∴∠B=∠E=30°,∠ACB=∠ACE=85°,
∴∠EAC=65°.
21.解:方法一 ∵,
∴,
∴.
方法二 ∵,,
∴,
∴,
∴.
22.解:∵△ACF≌△ADE,
∴AF=AE,
∴DF=AD-AF=AD-AE=9-4=5.
23.(1)解:.理由如下:
∵,
∴.
∵,,
∴.
(2).理由如下:
∵,
∴.
∵,,
∴.
24.证明:∵,
∴.
∵,
∴.
25.(1)解:设,,,
∵
∴,
解得.
.
∵,
∴;
(2)解:由(1)知,.
,
.
.
26.(1)解:,
,
,即.
点,,在一条直线上,
,
∴.
(2)解:由三角形外角的性质,得,
∴.
27.解:(1)∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE;
(2)△ABD满足∠ADB=90°时,BD∥CE,
理由是:∵△BAD≌△ACE,
∴∠E=∠ADB=90°,
∴∠BDE=180° 90°=90°=∠E,
∴BD∥CE.
28.(1)解:,
.
.
.
(2)解:,理由如下:
,
.
,
.
.
.
同课章节目录
