2016年4月海南省初中省级数学公开课比赛华师大版八上数学第14章 勾股定理第1节《勾股定理》教学课件(共37张PPT)
文档属性
| 名称 | 2016年4月海南省初中省级数学公开课比赛华师大版八上数学第14章 勾股定理第1节《勾股定理》教学课件(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-01 00:00:00 | ||
图片预览





文档简介
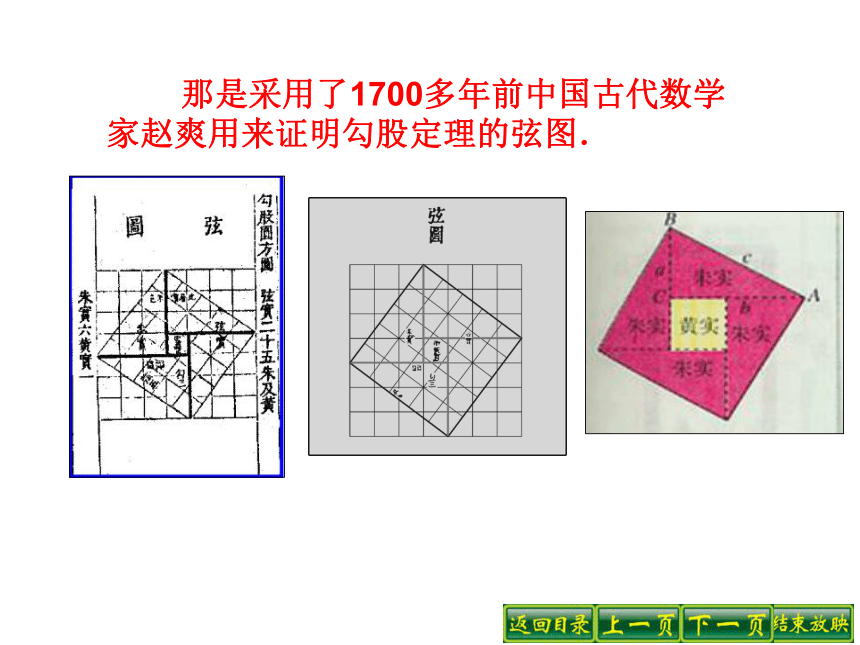
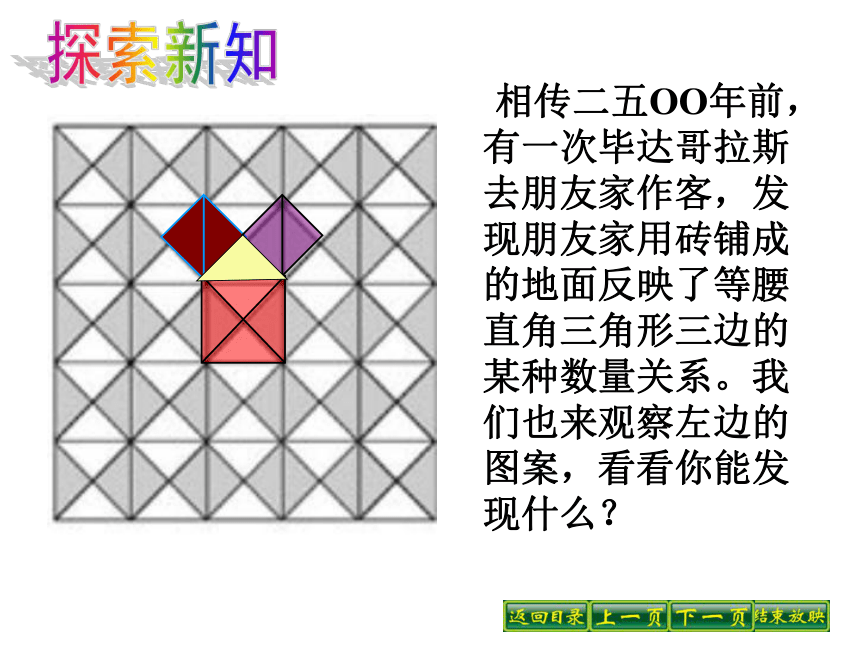
课件37张PPT。14.1勾股定理1.直角三角形三边的关系2002年在北京召开的国际数学家大会(ICM2002)。在那个大会上,到处可以看到一个简洁优美、远看像旋转的纸风车的图案就是大会的会标. 那是采用了1700多年前中国古代数学家赵爽用来证明勾股定理的弦图.探索新知 相传二五OO年前,有一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映了等腰直角三角形三边的某种数量关系。我们也来观察左边的图案,看看你能发现什么?正方形P 、 Q 、 R 的面积之间的关系是_________________.Rt△ABC的三边长度之间存在的关系是__________________.等腰直角三角形ABC中,两直角边的平方和等于斜边的平方. 那么在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?SP+SQ=SRAC2+BC2=AB2如果每一小方格表示1平方厘米,则
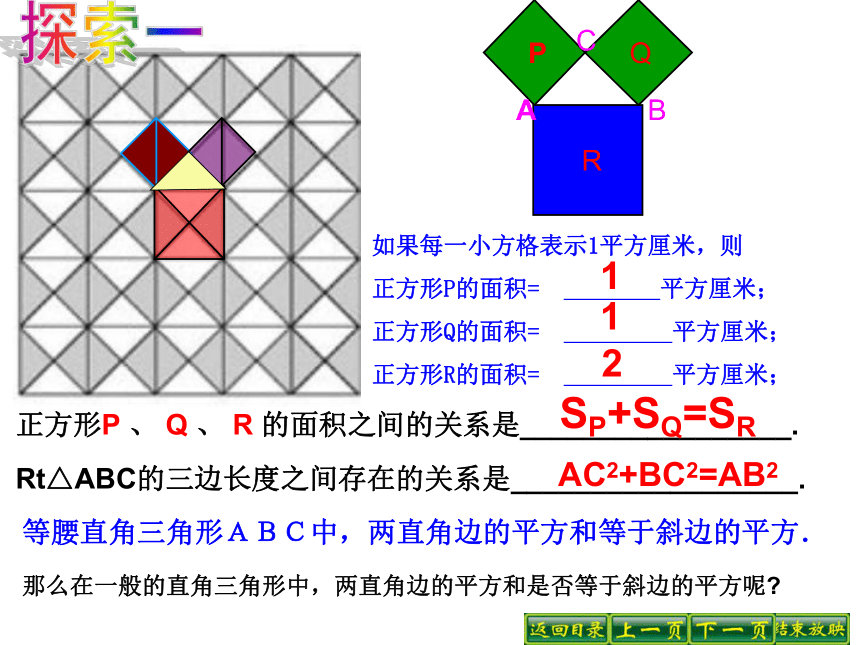
正方形P的面积= 平方厘米;
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米;
112探索一探索三正方形P的面积= 平方厘米;
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米.
正方形P、 Q、 R的面积之间的关系是 .
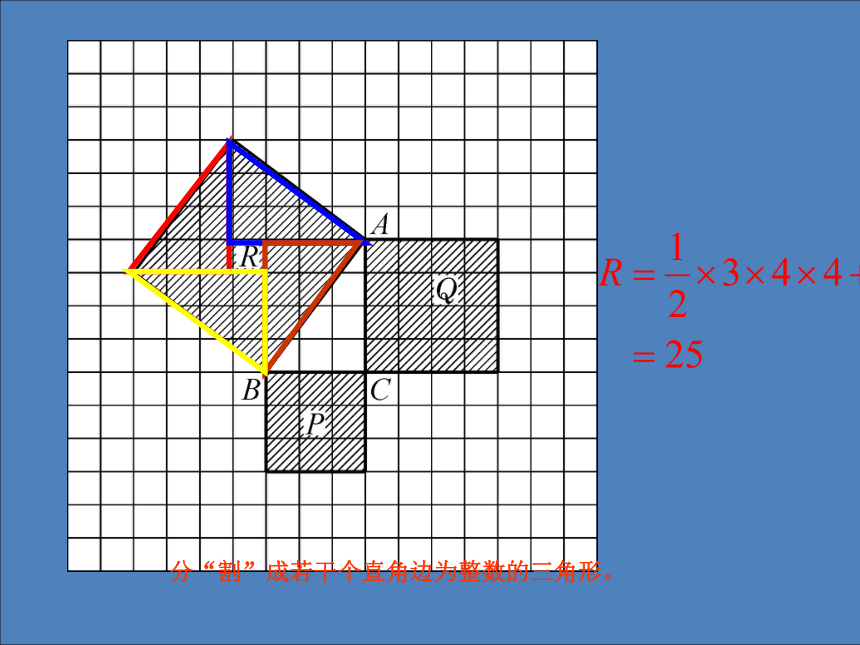
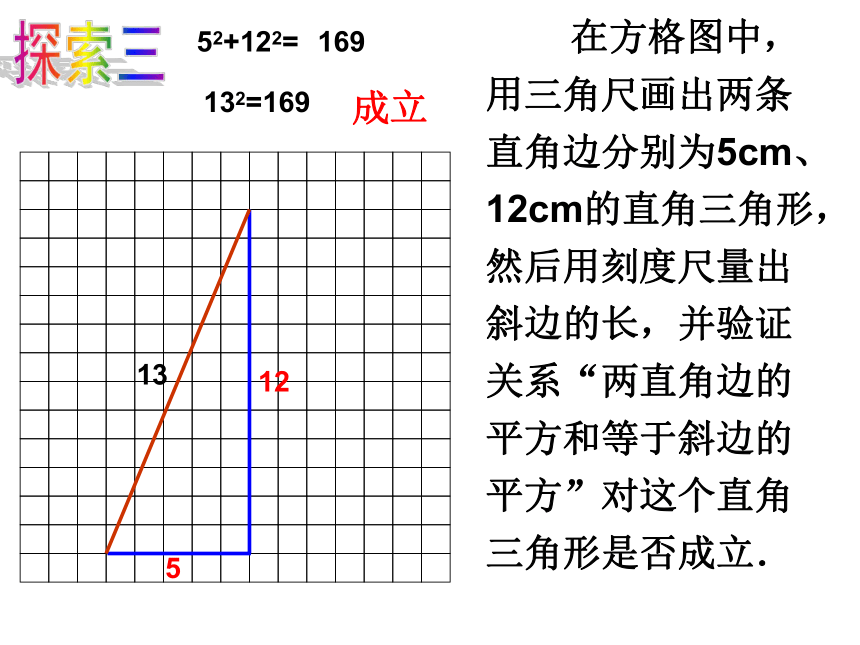
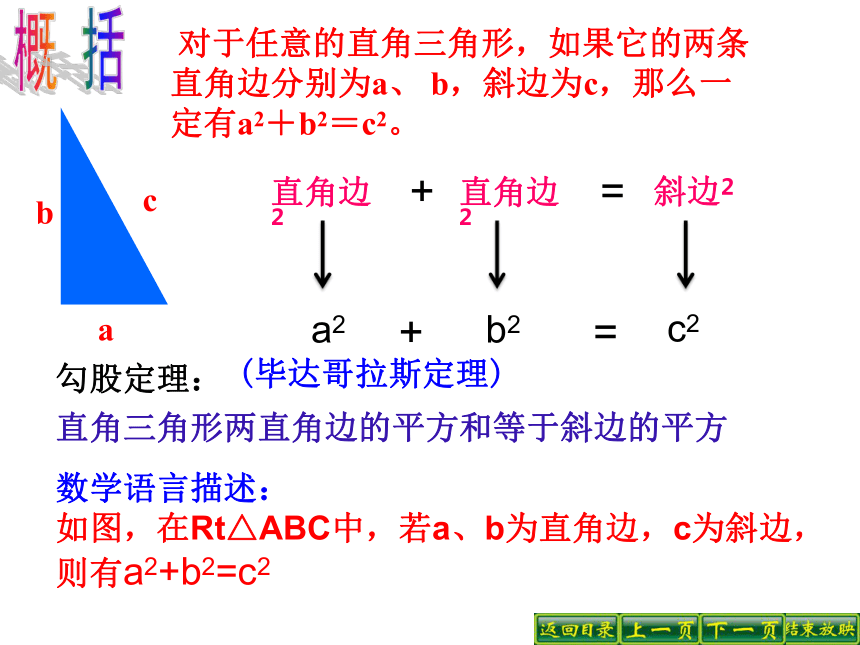
直角三角形ABC的三边的长度之间存在关系 .(每一小方格表示1平方厘米)91625P+ Q= RAC2+BC2=AB2在一般的直角三角形中,两直角边的平方和等于斜边的平方也成立! 分“割”成若干个直角边为整数的三角形。 在方格图中,用三角尺画出两条直角边分别为5cm、 12cm的直角三角形,然后用刻度尺量出斜边的长,并验证关系“两直角边的平方和等于斜边的平方”对这个直角三角形是否成立.5121352+122=169132=169成立探索三概 括 对于任意的直角三角形,如果它的两条直角边分别为a、 b,斜边为c,那么一定有a2+b2=c2。勾股定理:直角三角形两直角边的平方和等于斜边的平方数学语言描述:
如图,在Rt△ABC中,若a、b为直角边,c为斜边,则有a2+b2=c2(毕达哥拉斯定理) 读一读
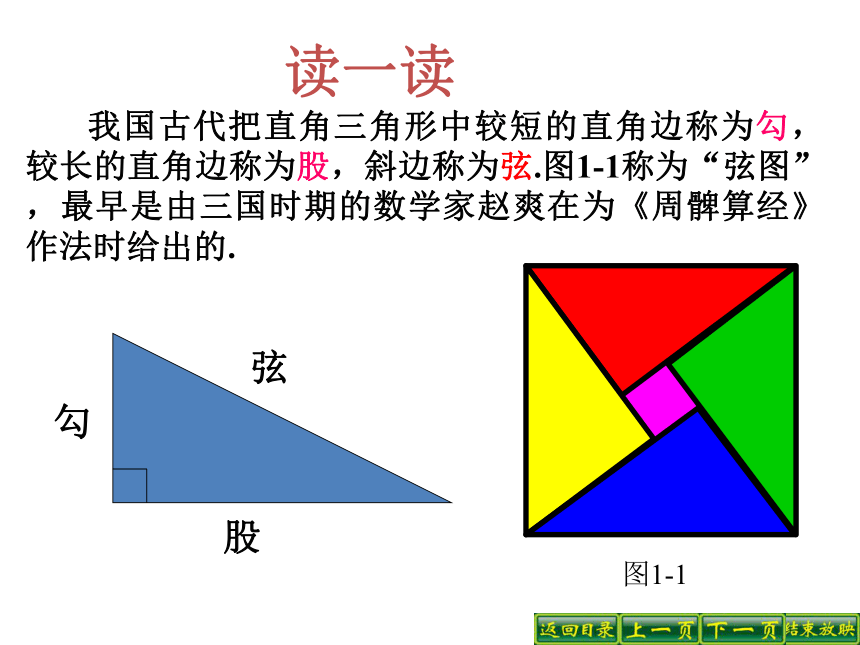
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的. 弦股勾图1-1 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。即∴(舍去负的)分析:由勾股定理得:
∴=5∴
例1:求出下列直角三角形中未知边x的长度应用新知(1)解:由勾股定理得:
(2)=8注意:要根据图形找出未知边是斜边还是直角边,勾股定理要用对。从上面这两道例题,我们知道了在直角三角形中,任意已知两边,可以求第三边。∴勾股定理的三个变形公式:(3)若已知b,c,由勾股定理得:如图,在Rt△ABC中,则求c的公式为:(1)若已知a,b,由勾股定理得:则求b的公式为:则求a的公式为:(2)若已知a,c,由勾股定理得:1. 如图,在直角三角形ABC中, ∠C=900,
已知: a=5, b=12, 求c
已知: b=8,c=10 , 求a
已知: a=7, c=25, 求b解:由勾股定理得:(2)(3) (1)小试牛刀2、若一个直角三角形的三边长分别为3,4, ,求第三边 的长度(精确到0.1)小试牛刀(2) 运用“勾股定理”时应注意什么问题?(1)这节课你学到了什么知识? ①勾股定理:直角三角形两直角边的平方和等于斜边的平方②在直角三角形中,任意已知两边,可以用勾股定理求第三边。小结 ①要利用图形找到未知边所在的直角三角形; ②看清未知边是所在直角三角形的哪一边;③勾股定理要用对。再见如图:已知四个全等的直角三角形的两直角边长分别为a和b,斜边长为c。利用这些直角三角形拼成一个大的正方形,来说明:
试一试做一做: P62540026xP的面积 =______________X=______225BACAB=__________AC=__________BC=__________251520
求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做X=81+1442Y=169-144Z=625-57622X=15Y=5Z=7结论:S1+S2+S3+S4=S5+S6=S7比一比看看谁算得快!3.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做例1如图14.1.4,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底边的垂直距离AB.(精确到0.01米)在Rt△ABC中,
BC=2.16米,AC=5.41米,
根据勾股定理可得
AB=
=
≈4.96(米).
答: 梯子上端A到墙的底边的垂直距离 AB 约为4.96米.5.142.16?解探索题拓展ACOBD 一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?试一试用四个完全相同的直角三角形,然后将它们拼成如图所示的图形.大正方形的面积可以表示为 。又可以表示为 .对比两种表示方法,看看能不能
得到勾股定理的结论.(a+b)2试一试用四个完全相同的直角三角形,还可以拼成如图所示的图形.大正方形的面积可以表示为 。又可以表示为 .对比两种表示方法,看看能不能得到勾股定理的结论.=┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.勾股弦 勾股定理(毕达哥拉斯定理) 如图,为了求出位于湖两岸的两点A、 B之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?如图14.1.9,在直角三角形ABC中,
AC=160米, BC=128米,
根据勾股定理可得
AB=
=
=96(米).
答: 从点A穿过湖到点B有96米.解例如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?9m24m1. 如图,小方格都是边长为1的正方形,求四边形ABCD的面积与周长.练习2. 假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏埋藏点B的直线距离是多少千米?证法课堂小结
勾股定理直角三角形两直角边的平方和等于斜边的平方再见
正方形P的面积= 平方厘米;
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米;
112探索一探索三正方形P的面积= 平方厘米;
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米.
正方形P、 Q、 R的面积之间的关系是 .
直角三角形ABC的三边的长度之间存在关系 .(每一小方格表示1平方厘米)91625P+ Q= RAC2+BC2=AB2在一般的直角三角形中,两直角边的平方和等于斜边的平方也成立! 分“割”成若干个直角边为整数的三角形。 在方格图中,用三角尺画出两条直角边分别为5cm、 12cm的直角三角形,然后用刻度尺量出斜边的长,并验证关系“两直角边的平方和等于斜边的平方”对这个直角三角形是否成立.5121352+122=169132=169成立探索三概 括 对于任意的直角三角形,如果它的两条直角边分别为a、 b,斜边为c,那么一定有a2+b2=c2。勾股定理:直角三角形两直角边的平方和等于斜边的平方数学语言描述:
如图,在Rt△ABC中,若a、b为直角边,c为斜边,则有a2+b2=c2(毕达哥拉斯定理) 读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的. 弦股勾图1-1 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。即∴(舍去负的)分析:由勾股定理得:
∴=5∴
例1:求出下列直角三角形中未知边x的长度应用新知(1)解:由勾股定理得:
(2)=8注意:要根据图形找出未知边是斜边还是直角边,勾股定理要用对。从上面这两道例题,我们知道了在直角三角形中,任意已知两边,可以求第三边。∴勾股定理的三个变形公式:(3)若已知b,c,由勾股定理得:如图,在Rt△ABC中,则求c的公式为:(1)若已知a,b,由勾股定理得:则求b的公式为:则求a的公式为:(2)若已知a,c,由勾股定理得:1. 如图,在直角三角形ABC中, ∠C=900,
已知: a=5, b=12, 求c
已知: b=8,c=10 , 求a
已知: a=7, c=25, 求b解:由勾股定理得:(2)(3) (1)小试牛刀2、若一个直角三角形的三边长分别为3,4, ,求第三边 的长度(精确到0.1)小试牛刀(2) 运用“勾股定理”时应注意什么问题?(1)这节课你学到了什么知识? ①勾股定理:直角三角形两直角边的平方和等于斜边的平方②在直角三角形中,任意已知两边,可以用勾股定理求第三边。小结 ①要利用图形找到未知边所在的直角三角形; ②看清未知边是所在直角三角形的哪一边;③勾股定理要用对。再见如图:已知四个全等的直角三角形的两直角边长分别为a和b,斜边长为c。利用这些直角三角形拼成一个大的正方形,来说明:
试一试做一做: P62540026xP的面积 =______________X=______225BACAB=__________AC=__________BC=__________251520
求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做X=81+1442Y=169-144Z=625-57622X=15Y=5Z=7结论:S1+S2+S3+S4=S5+S6=S7比一比看看谁算得快!3.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做例1如图14.1.4,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底边的垂直距离AB.(精确到0.01米)在Rt△ABC中,
BC=2.16米,AC=5.41米,
根据勾股定理可得
AB=
=
≈4.96(米).
答: 梯子上端A到墙的底边的垂直距离 AB 约为4.96米.5.142.16?解探索题拓展ACOBD 一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?试一试用四个完全相同的直角三角形,然后将它们拼成如图所示的图形.大正方形的面积可以表示为 。又可以表示为 .对比两种表示方法,看看能不能
得到勾股定理的结论.(a+b)2试一试用四个完全相同的直角三角形,还可以拼成如图所示的图形.大正方形的面积可以表示为 。又可以表示为 .对比两种表示方法,看看能不能得到勾股定理的结论.=┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.勾股弦 勾股定理(毕达哥拉斯定理) 如图,为了求出位于湖两岸的两点A、 B之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?如图14.1.9,在直角三角形ABC中,
AC=160米, BC=128米,
根据勾股定理可得
AB=
=
=96(米).
答: 从点A穿过湖到点B有96米.解例如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?9m24m1. 如图,小方格都是边长为1的正方形,求四边形ABCD的面积与周长.练习2. 假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏埋藏点B的直线距离是多少千米?证法课堂小结
勾股定理直角三角形两直角边的平方和等于斜边的平方再见
