五四制鲁教版数学一轮复习 第四章 三角形 专项训练 相似三角形相关常考模型(含答案)
文档属性
| 名称 | 五四制鲁教版数学一轮复习 第四章 三角形 专项训练 相似三角形相关常考模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-16 17:07:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第四章 三角形
专项训练 相似三角形相关常考模型
模型一 8字型
【模型分析】
有一组隐含的等角(对顶角),此时需要从已知条件、图中隐含条件或通过证明得另一对角相等.另外,若题中未明确相似三角形对应顶点,则需要分类讨论.
【针对训练】
1.如图,在梯形ABCD中,AD∥BC,对角线AC 和 BD 交于点 O,若 则
2.如图,菱形ABCD 的边长为6,∠BAD=120°,过点 D 作 DE⊥BC,交 BC 的延长线于点 E,连接AE 分别交 BD,CD 于点F,G,则FG的长为 .
模型二 A字型
【模型分析】
有一个公共角(图①和图②)或角有公共角(图③中∠DAF +∠BAD =∠DAF +∠EAF),此时需要找另一对角相等.另外,若题中未明确相似三角形对应顶点,则需要分类讨论,如图③中可找条件∠D=∠C或∠D=∠B.
【针对训练】
3.如图,在△ABC中,点D,E分别为边AB,AC的中点.下列结论中,错误的是( )
A.DE∥BC B.△ADE∽△ABC C.BC=2DE
4.如图,在△ABC中,AB =6,BC=8,点P为AB上一点,过点P作PQ∥BC交AC于点Q.设AP 的长度为x,点P,Q的距离为y1,△ABC的周长与△APQ的周长之比为y2.
(1)请直接写出y1,y2分别关于x的函数表达式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出函数y1,y2的图象;请分别写出函数y1,y2的一条性质;
(3)结合函数图象,直接写出 时x的取值范围.(近似值保留一位小数,误差不超过0.2)
模型三 母子型
【模型分析】
有一个公共角,且公共角的一边为公共边;需要从已知条件、图中隐含条件或通过证明得另一对角相等,此时 AB(AC 为公共边,AD,AB为有部分重合的边).
【针对训练】
5.如图,在 Rt△ABC 中,∠C =90°,AD 是△ABC 的一条角平分线,E 为AD 中点,连接 BE. 若 BE = BC,CD =2,则 BD =
模型四 手拉手型
【模型分析】
模型展示
模型特点 △AOB∽△COD,且绕公共顶点O旋转,简记为:非等腰,共顶点,顶角相等,旋转得相似
结 论 ①△AOC∽△BOD;②; ③两条拉手线AC,BD所在直线的夹角与∠AOB相等或互补
【针对训练】
6.如图,△ABC∽△ADE,∠BAC=∠DAE=90°,AB=8,AC=6,F是DE 的中点.若点 E 是直线BC 上的动点,连接BF,则BF的最小值是 .
第6题图 第7题图
7.如图,在直角坐标系中,点A,B的坐标为A(0,2),B(-1,0),将△ABO绕点 O 按顺时针旋转得到△A B O,若AB⊥OB ,则点A 的坐标为( )
模型五 一线三等角
【模型分析】
通过三角形内外角关系、内角和、直角三角形的两锐角互余等性质找一组对应角相等.
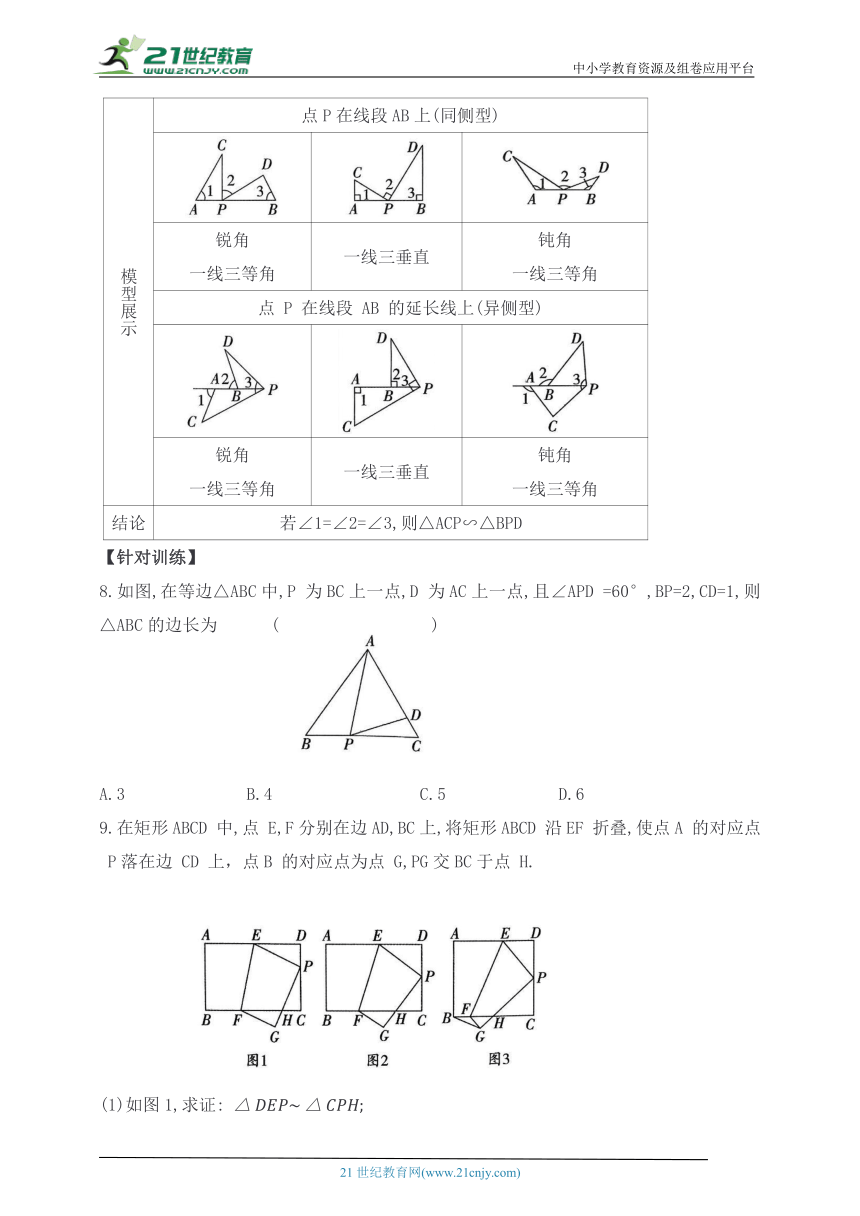
模型展示 点P在线段AB上(同侧型)
锐角 一线三等角 一线三垂直 钝角 一线三等角
点 P 在线段 AB 的延长线上(异侧型)
锐角 一线三等角 一线三垂直 钝角 一线三等角
结论 若∠1=∠2=∠3,则△ACP∽△BPD
【针对训练】
8.如图,在等边△ABC中,P 为BC上一点,D 为AC上一点,且∠APD =60°,BP=2,CD=1,则△ABC的边长为 ( )
A.3 B.4 C.5 D.6
9.在矩形ABCD 中,点 E,F分别在边AD,BC上,将矩形ABCD 沿EF 折叠,使点A 的对应点 P落在边 CD 上,点B 的对应点为点 G,PG交BC于点 H.
(1)如图1,求证:
(2)如图2,当P 为 CD 的中点, 时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究 BG 与 AB 的数量关系,并说明理由.
参考答案
1.
解析:∵ 菱形 ABCD 的边长为6,∠BAD =120°,∴ AD = BC =CD=6,AD∥BC,∠BCD =120°,∴∠DCE=60°.
∵DE⊥BC,∴ ∠DEC=90°.在 Rt△DCE 中,
∵ ∠CDE =
+CE =9.
∵ AD∥BE,∴∠ADE =180°-∠DEC =90°.
在 Rt△ADE 中, 3.
∵AD∥BE,∴△AFD∽F
∥
3. D
4.解:
(2)函数y ,y 的图象如图所示.
当0<x≤6时,y 随x的增大而增大;y 随x的增大而减小.
(3)由函数图象,得当 时x的取值范围为2.1<x≤6.
解析:连接CE,过点 E 作 EF⊥BC于点 F,如图.
设BD =x,则BC=BD+CD =x+2.
∵ ∠ACB =90°,E 为 AD 中点,∴CE=AE =DE= AD,∴∠CAE =∠ACE,∠ECD=∠EDC,∴ ∠CED =2∠CAD.
∵BE = BC,∴ ∠ECD = ∠BEC,∴∠BEC = ∠EDC.
∵AD平分∠CAB,∴ ∠CAB =2∠CAD,∴ ∠CAB = ∠CED,∴ ∠CAB =∠CBE.
∵ ∠ACB = 90°= ∠BFE,∴△ABC∽△BEF,∴ACF=BCF.
E为AD中点,∴AC=
解得 或 (不合题意,舍去), ∴BD
6.4 解析:如图,连接 BD.
设 AB Dr与 DE 交于点O.
∵ △ABC∽△ADE,∴ ∠ADE = ∠ABE.
又∵∠AOD = ∠EOB, ∴ △ADO ∽
又∵ ∠DOB = ∠AOE,∴ △BDO ∽△EAO,∴ ∠DBO = ∠AEO.
又∵∠DBE=∠DBO +∠ABE = ∠AED+∠ADO=90°,∴BF= DE,
∴当DE最小时,BF最小.
∵当AE⊥BC时,AE最小,此时DE最小.
∵BC=
E=8,∴ BF的最小值为4.
7. A 解析:如图,设AB 交 OB 于点 T,过点 A 作 A R⊥x轴于.R.
∵A(0,2),B(-1,0),∴OB=1,OA =2,∴ AB =
∠A OB = 90°, ∴ ∠AOT =∠A OR.
∵ ∠ATO =∠A RO =90°,
8. B
9.解:(1)如图,
∵四边形ABCD 是矩形,∴∠A=∠D=∠C=90°,∴∠1+∠3=90°.
∵点E,F 分别在AD,BC 上,将四边形 ABFE 沿 EF 翻折,使点 A 的对称点 P 落在DC上,∴∠EPH=∠A=90°,∴∠1+∠2=90°,∴∠3=∠2,∴△DEP∽△CPH.
(2)∵四边形ABCD 是矩形,∴CD=AB =2,AD=BC=3,∠A =∠D=∠C=90°.
∵P为CD中点,
设EP=AE=x,∴ED=AD-x=3-x.
在Rt△EDP中, 即 解得
即
理由如下:
如图,延长 AB,PG 交于点 M,连接AP.
∵点E,F分别在AD,BC上,将四边形ABFE沿 EF 翻折,使点 A的对称点 P 落在 CD上,∴AP⊥EF,BG⊥直线EF,∴ BG∥AP.
∵AE=EP,∴∠EAP =∠EPA,∴∠BAP=∠GPA,∴ △MAP是等腰三角形,∴MA=MP.
∵ P为 CD 中点,∴设 DP =CP=y,∴AB=PG=CD=2y.
∵H为 BC中点,∴ BH=CH.
∵∠BHM=∠CHP,∠CBM=∠PCH,∴△MBH≌△PCH(ASA),
在 中, 在 中,
∥
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 三角形
专项训练 相似三角形相关常考模型
模型一 8字型
【模型分析】
有一组隐含的等角(对顶角),此时需要从已知条件、图中隐含条件或通过证明得另一对角相等.另外,若题中未明确相似三角形对应顶点,则需要分类讨论.
【针对训练】
1.如图,在梯形ABCD中,AD∥BC,对角线AC 和 BD 交于点 O,若 则
2.如图,菱形ABCD 的边长为6,∠BAD=120°,过点 D 作 DE⊥BC,交 BC 的延长线于点 E,连接AE 分别交 BD,CD 于点F,G,则FG的长为 .
模型二 A字型
【模型分析】
有一个公共角(图①和图②)或角有公共角(图③中∠DAF +∠BAD =∠DAF +∠EAF),此时需要找另一对角相等.另外,若题中未明确相似三角形对应顶点,则需要分类讨论,如图③中可找条件∠D=∠C或∠D=∠B.
【针对训练】
3.如图,在△ABC中,点D,E分别为边AB,AC的中点.下列结论中,错误的是( )
A.DE∥BC B.△ADE∽△ABC C.BC=2DE
4.如图,在△ABC中,AB =6,BC=8,点P为AB上一点,过点P作PQ∥BC交AC于点Q.设AP 的长度为x,点P,Q的距离为y1,△ABC的周长与△APQ的周长之比为y2.
(1)请直接写出y1,y2分别关于x的函数表达式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出函数y1,y2的图象;请分别写出函数y1,y2的一条性质;
(3)结合函数图象,直接写出 时x的取值范围.(近似值保留一位小数,误差不超过0.2)
模型三 母子型
【模型分析】
有一个公共角,且公共角的一边为公共边;需要从已知条件、图中隐含条件或通过证明得另一对角相等,此时 AB(AC 为公共边,AD,AB为有部分重合的边).
【针对训练】
5.如图,在 Rt△ABC 中,∠C =90°,AD 是△ABC 的一条角平分线,E 为AD 中点,连接 BE. 若 BE = BC,CD =2,则 BD =
模型四 手拉手型
【模型分析】
模型展示
模型特点 △AOB∽△COD,且绕公共顶点O旋转,简记为:非等腰,共顶点,顶角相等,旋转得相似
结 论 ①△AOC∽△BOD;②; ③两条拉手线AC,BD所在直线的夹角与∠AOB相等或互补
【针对训练】
6.如图,△ABC∽△ADE,∠BAC=∠DAE=90°,AB=8,AC=6,F是DE 的中点.若点 E 是直线BC 上的动点,连接BF,则BF的最小值是 .
第6题图 第7题图
7.如图,在直角坐标系中,点A,B的坐标为A(0,2),B(-1,0),将△ABO绕点 O 按顺时针旋转得到△A B O,若AB⊥OB ,则点A 的坐标为( )
模型五 一线三等角
【模型分析】
通过三角形内外角关系、内角和、直角三角形的两锐角互余等性质找一组对应角相等.
模型展示 点P在线段AB上(同侧型)
锐角 一线三等角 一线三垂直 钝角 一线三等角
点 P 在线段 AB 的延长线上(异侧型)
锐角 一线三等角 一线三垂直 钝角 一线三等角
结论 若∠1=∠2=∠3,则△ACP∽△BPD
【针对训练】
8.如图,在等边△ABC中,P 为BC上一点,D 为AC上一点,且∠APD =60°,BP=2,CD=1,则△ABC的边长为 ( )
A.3 B.4 C.5 D.6
9.在矩形ABCD 中,点 E,F分别在边AD,BC上,将矩形ABCD 沿EF 折叠,使点A 的对应点 P落在边 CD 上,点B 的对应点为点 G,PG交BC于点 H.
(1)如图1,求证:
(2)如图2,当P 为 CD 的中点, 时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究 BG 与 AB 的数量关系,并说明理由.
参考答案
1.
解析:∵ 菱形 ABCD 的边长为6,∠BAD =120°,∴ AD = BC =CD=6,AD∥BC,∠BCD =120°,∴∠DCE=60°.
∵DE⊥BC,∴ ∠DEC=90°.在 Rt△DCE 中,
∵ ∠CDE =
+CE =9.
∵ AD∥BE,∴∠ADE =180°-∠DEC =90°.
在 Rt△ADE 中, 3.
∵AD∥BE,∴△AFD∽F
∥
3. D
4.解:
(2)函数y ,y 的图象如图所示.
当0<x≤6时,y 随x的增大而增大;y 随x的增大而减小.
(3)由函数图象,得当 时x的取值范围为2.1<x≤6.
解析:连接CE,过点 E 作 EF⊥BC于点 F,如图.
设BD =x,则BC=BD+CD =x+2.
∵ ∠ACB =90°,E 为 AD 中点,∴CE=AE =DE= AD,∴∠CAE =∠ACE,∠ECD=∠EDC,∴ ∠CED =2∠CAD.
∵BE = BC,∴ ∠ECD = ∠BEC,∴∠BEC = ∠EDC.
∵AD平分∠CAB,∴ ∠CAB =2∠CAD,∴ ∠CAB = ∠CED,∴ ∠CAB =∠CBE.
∵ ∠ACB = 90°= ∠BFE,∴△ABC∽△BEF,∴ACF=BCF.
E为AD中点,∴AC=
解得 或 (不合题意,舍去), ∴BD
6.4 解析:如图,连接 BD.
设 AB Dr与 DE 交于点O.
∵ △ABC∽△ADE,∴ ∠ADE = ∠ABE.
又∵∠AOD = ∠EOB, ∴ △ADO ∽
又∵ ∠DOB = ∠AOE,∴ △BDO ∽△EAO,∴ ∠DBO = ∠AEO.
又∵∠DBE=∠DBO +∠ABE = ∠AED+∠ADO=90°,∴BF= DE,
∴当DE最小时,BF最小.
∵当AE⊥BC时,AE最小,此时DE最小.
∵BC=
E=8,∴ BF的最小值为4.
7. A 解析:如图,设AB 交 OB 于点 T,过点 A 作 A R⊥x轴于.R.
∵A(0,2),B(-1,0),∴OB=1,OA =2,∴ AB =
∠A OB = 90°, ∴ ∠AOT =∠A OR.
∵ ∠ATO =∠A RO =90°,
8. B
9.解:(1)如图,
∵四边形ABCD 是矩形,∴∠A=∠D=∠C=90°,∴∠1+∠3=90°.
∵点E,F 分别在AD,BC 上,将四边形 ABFE 沿 EF 翻折,使点 A 的对称点 P 落在DC上,∴∠EPH=∠A=90°,∴∠1+∠2=90°,∴∠3=∠2,∴△DEP∽△CPH.
(2)∵四边形ABCD 是矩形,∴CD=AB =2,AD=BC=3,∠A =∠D=∠C=90°.
∵P为CD中点,
设EP=AE=x,∴ED=AD-x=3-x.
在Rt△EDP中, 即 解得
即
理由如下:
如图,延长 AB,PG 交于点 M,连接AP.
∵点E,F分别在AD,BC上,将四边形ABFE沿 EF 翻折,使点 A的对称点 P 落在 CD上,∴AP⊥EF,BG⊥直线EF,∴ BG∥AP.
∵AE=EP,∴∠EAP =∠EPA,∴∠BAP=∠GPA,∴ △MAP是等腰三角形,∴MA=MP.
∵ P为 CD 中点,∴设 DP =CP=y,∴AB=PG=CD=2y.
∵H为 BC中点,∴ BH=CH.
∵∠BHM=∠CHP,∠CBM=∠PCH,∴△MBH≌△PCH(ASA),
在 中, 在 中,
∥
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
