五四制鲁教版数学一轮复习 第四章 三角形 第1节 几何初步认识(含答案)
文档属性
| 名称 | 五四制鲁教版数学一轮复习 第四章 三角形 第1节 几何初步认识(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 687.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-16 17:08:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第四章 三角形
第1节 几何初步认识
考点分析
考点1 直线、射线、线段
课标要求导航:
①通过实物和模型,了解从物体抽象出来的几何体、平面、直线和点等概念;
②会比较线段的长短,理解线段的和、差,以及线段中点的意义;
③掌握基本事实:两点确定一条直线;④掌握基本事实:两点之间线段最短;
⑤理解两点间距离的意义,能度量和表达两点间的距离.
例1 汽车灯所射出的光线可以近似地看成 ( )
A.线段 B.射线 C.直线 D.曲线
1.1 直线、线段、射线的位置如图所示,如图中能相交的是 ( )
例2 如图,点B 是线段AC上一点,且
(1)求线段AC的长;
(2)若点O 是线段AC 的中点,求线段OB 的长.
2.1 平面上有三点A,B,C,若AB=8,AC=5,BC=3,则 ( )
A.点 C 在线段AB 上 B.点 C 在线段AB 的延长线上
C.点 C 在线段AB 外 D.点C 可能在AB 上,也可能在AB 外
考点2 角
课标要求导航:理解角的概念,能比较角的大小;认识度、分、秒等角的度量单位,能进行简单的单位换算,会计算角的和、差.
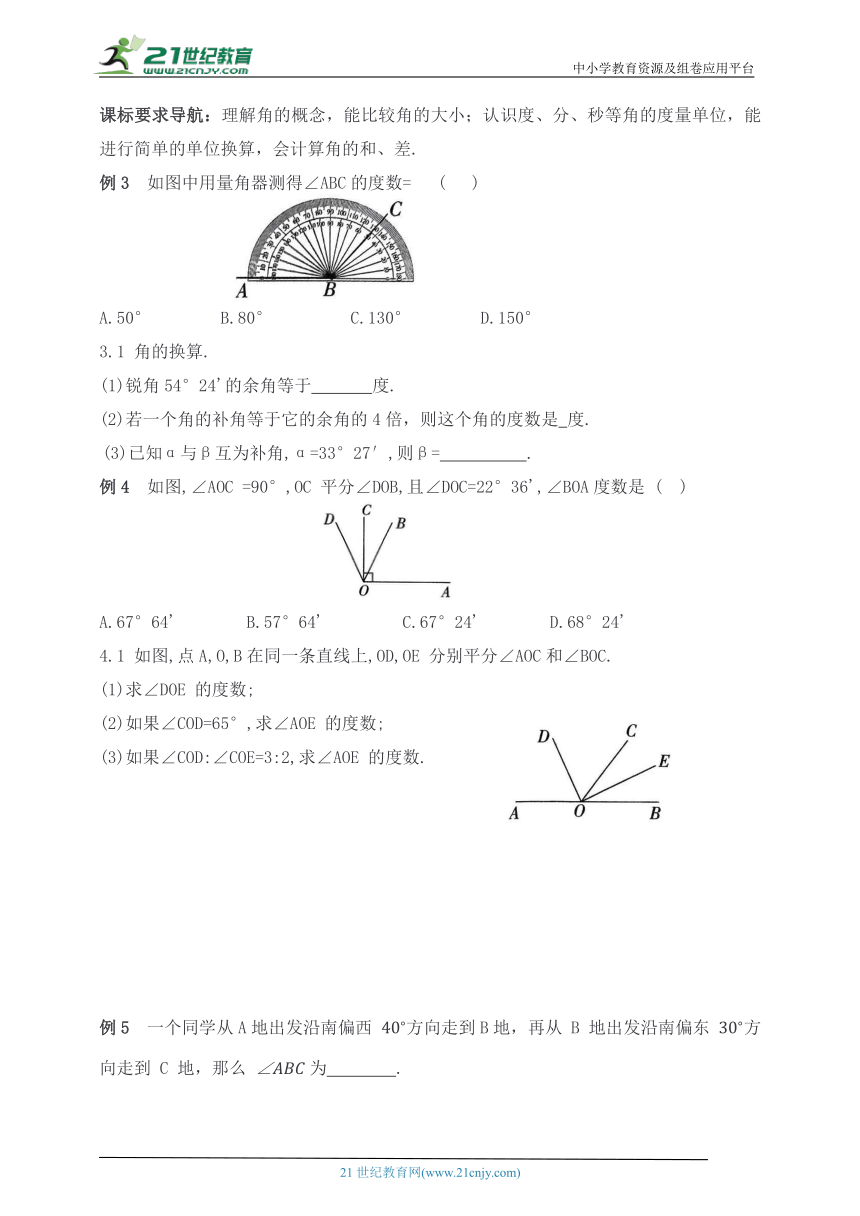
例3 如图中用量角器测得∠ABC的度数= ( )
A.50° B.80° C.130° D.150°
3.1 角的换算.
(1)锐角54°24'的余角等于 度.
(2)若一个角的补角等于它的余角的4倍,则这个角的度数是 度.
(3)已知α与β互为补角,α=33°27′,则β= .
例4 如图,∠AOC =90°,OC 平分∠DOB,且∠DOC=22°36',∠BOA度数是 ( )
A.67°64' B.57°64' C.67°24' D.68°24'
4.1 如图,点A,O,B在同一条直线上,OD,OE 分别平分∠AOC和∠BOC.
(1)求∠DOE 的度数;
(2)如果∠COD=65°,求∠AOE 的度数;
(3)如果∠COD:∠COE=3:2,求∠AOE 的度数.
例5 一个同学从A地出发沿南偏西 方向走到B地,再从 B 地出发沿南偏东 方向走到 C 地,那么 为 .
5.1 如图,在灯塔O 处观测到轮船A位于北偏西 的方向,同时轮船B 在南偏东 的方向,那么
考点3 相交线与平行线
类型1 相交线
课标要求导航:
①理解对顶角、余角、补角等概念,探索并掌握对顶角相等、同角(或等角)的余角相等、同角(或等角)的补角相等的性质;
②理解垂线、垂线段等概念,能用三角板或量角器过一点画已知直线的垂线;
③掌握基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直;
④理解点到直线的距离的意义,能度量点到直线的距离.
例6 如图,直线AB,CD 相交于点 O.若 则 的度数为 ( )
A.70°
6.1 如图,直线AB,CD 相交于点O,OE 平分 若 则 的度数为 ( )
A.46° B.56° C.67° D.77°
例7 如图,要把河中的水引到水池A中,应在河岸 B 处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是 ( )
A.点到直线的距离 B.垂线段最短
C.两点确定一条直线 D.两点之间线段最短
类型2 平行线的性质与判定
课标要求导航:
①识别同位角、内错角、同旁内角;
②理解平行线的概念;
③掌握平行线基本事实Ⅰ:过直线外一点有且只有一条直线与这条直线平行;
④掌握平行线基本事实Ⅱ:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;
⑤探索并证明平行线的判定定理:两条直线被第三条直线所截,如果内错角相等(或同旁内角互补),那么这两条直线平行;
⑥掌握平行线的性质定理Ⅰ:两条平行直线被第三条直线所截,同位角相等.了解定理的证明;
⑦探索并证明平行线的性质定理Ⅱ:两条平行直线被第三条直线所截,内错角相等(或同旁内角互补);
⑧能用三角板和直尺过已知直线外一点画这条直线的平行线;
⑨能用尺规作图:过直线外一点作这条直线的平行线;
⑩了解平行于同一条直线的两条直线平行.
例8 一把直尺和一个含30°角的直角三角板按如图i方式放置,若∠1=20°,则∠2= ( )
A.30° B.40° C.50° D.60°
8.1 如图,AB∥CD,点 E在线段 BC上(不与点B,C重合),连接DE.若∠D=40°,∠BED=60°,则∠B= ( )
A.10° B.20° C.40° D.60°
8.2 如图,已知AD∥BC,BD 平分∠ABC.若∠A=110°,则∠D 的度数是 ( )
A.40° B.36° C.35° D.30°
8.3 已知直线a,b被c,d所截,若∠1=∠2=60°,∠3=55°,则∠4 的度数是( )
A.60° B.55° C.120° D.125°
8.4 一杆古秤在称物时的状态如图所示,已知∠1=102°,则∠2的度数为 .
8.5 如图,AB∥CD,AD∥BC,AD=5,BE=8,△DCE的面积为6,则四边形ABCD的面积为
例9 已知∠AOB,点 P 为OA上一点,用尺规作图,过点 P 作OB 的平行线.下列作图痕迹不正确的是 ( )
考点4 线段的垂直平分线、角平分线
课标要求导航:
①理解角平分线的概念,探索并证明角平分线的性质定理:角平分线上的点到角两边的距离相等;反之,角的内部到角两边距离相等的点在角的平分线上;
②理解线段垂直平分线的概念,探索并证明线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等;反之,到线段两端距离相等的点在线段的垂直平分线上;
③能用尺规作图:作一个角的平分线;
④能用尺规作图:作一条线段的垂直平分线.
例10 如图,在中,AC的垂直平分线交BC于点D,交AC于点E,若则DC的长是 .
10.1 如图,在 中, ,DE垂直平分AB交BC于点D,若 的周长为50cm,则AC+BC= ( )
A.25 cm B.45 cm C.50cm D.55 cm
【思路点拨】根据线段垂直平分线得出 ,进而利用三角形的周长解答即可.
10.2 尺规作图 在 内找一点 P,使点 P 到A,B两点的距离相等,并且点 P 到点 C 的距离等于线段AC的长.
10.3 如图,在 中,边AB 的垂直平分线分别交BC,AB于点E,M,边AC的垂直平分线分别交BC,AC于点 F,N,BE
(1)求 的长;
(2)若 求 的面积.
例11 如图,△ABC中,∠A=90°,AB=8,AC=15,以点 B 为圆心,适当长为半径画弧,分别交 BA,BC 于点 M,N,再分别以点 M,N为圆心,大于 的长为半径画弧,两弧交于点E,作射线 BE 交AC 于点 D,则线段AD 的长为 .
11.1 尺规作图 如图,△ABC 中, ,垂足为 D.求作∠ABC 的平分线,分别交AD,AC 于 P,Q 两点.(要求:尺规作图,保留作图痕迹,不写作法)
考点5 命题、定理与证明
课标要求导航:
①通过具体实例,了解定义、命题、定理、推论的意义;
②结合具体实例,会区分命题的条件和结论,了解原命题及其逆命题的概念.会识别两个互逆的命题,知道原命题成立其逆命题不一定成立;
③知道证明的意义和证明的必要性,知道数学思维要合乎逻辑,知道可以用不同的形式表述证明的过程,会用综合法的证明格式;
④了解反例的作用,知道利用反例可以判断一个命题是错误的.
例12 下列命题中,正确的是 ( )
A.两点之间,线段最短 B.菱形的对角线相等
C.正五边形的外角和为 D.直角三角形是轴对称图形
【思路点拨】根据两点之间,线段最短、菱形的性质、正多边形的外角和、轴对称图形的概念判断即可.
12.1 下列命题是真命题的是 ( )
A.同位角相等 B.菱形的四条边相等
C.正五边形是中心对称图形 D.单项式 的次数是4
12.2 对于命题“如果 ,那么 ”能说明它是假命题的反例是 ( )
达标训练
基础达标特训
1.若∠A =80°,则∠A 的补角是 ( )
A.100° B.80° C.40° D.10°
2.如图,乙地在甲地的北偏东50°方向上,则∠1 的度数为 ( )
A.60° B.50° C.40° D.30°
3.如图,在纸上画有∠AOB,将两把直尺按图示摆放,直尺边缘的交点 P在∠AOB的平分线上,则 ( )
A. 与 一定相等 B. 与 一定不相等
C. 与 一定相等 D. 与 一定不相等
4.跨学科·物理 如图,推动水桶,以点O为支点,使其向右倾斜.若在点A 处分别施加推力 F ,F ,则 F 的力臂 OA大于 F 的力臂OB.这一判断过程体现的数学依据是 ( )
A.垂线段最短 B.过一点有且只有一条直线与已知直线垂直
C.两点确定一条直线 D.过直线外一点有且只有一条直线与已知直线平行
5.如图,直线m∥n,一块含有30°的直角三角板按如图所示放置.若∠1 =40°,则∠2的大小为 ( )
A.70° B.60° C.50° D.40°
6.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB 于E,垂足为D.如果 CE=10,则ED的长为 ( )
A.3 B.4 C.5 D.6
7.如图,小明在地图上量得∠1=∠2,由此判断幸福大街与平安大街互相平行,他判断的依据是 ( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.对顶角相等
8.如图,AB∥CD,AD 平分∠BAC,∠1=30°,则∠2= ( )
A.15° B.30° C.45° D.60°
9.如图,一条公路的两侧铺设了AB,CD两条平行管道,并有纵向管道AC连通,若∠1 =120°,则∠2 的度数是 ( )
A.50° B.60° C.70° D.80°
10.如图,A,B,C,D,E,P,Q,R,S,T是构成五角星的五条线段的交点,则图中共有线
段 条.
11. 已知∠A =30°45',∠B =30. 45°,则∠A ∠B.(填“>”“<”或“=”)
高分提能特训
12.如图,两个平面镜平行放置,光线经过平面镜反射时,∠1 =∠2=40°,则∠3 的度数为 ( )
A.80° B.90° C.100° D.120°
13.如图,在△ABC 中,∠ABC A=90°,∠C=30°,以点A 为圆心,以AB 的长为半径作弧交AC于点D,连接BD,再分别以点B,D为圆心,大于 BD 的长为半径作弧,两弧交于点 P,作射线AP 交 BC于点E,连接DE,则下列结论中不正确的是 ( )
A. BE=DE B. AE=CE C. CE=2BE
14.综合与实践 如图,在一次综合实践课上,为检验纸带①、②的边线是否平行,小庆和小铁采用了两种不同的方法:小庆把纸带①沿 AB 折叠,量得∠1 =∠2=59°;小铁把纸带②沿 GH 折叠,发现GD与GC重合,HF 与HE 重合,且点 C,G,D在同一直线上,点E,H,F也在同一直线上.则下列判断正确的是( )
A.纸带①、②的边线都平行
B.纸带①、②的边线都不平行
C.纸带①的边线平行,纸带②的边线不平行
D.纸带①的边线不平行,纸带②的边线平行
15.跨学科·物理 如图,在空心圆柱口放置一面平面镜EF,EF 与水平线CD的夹角∠EBC=70°,人射光线AB经平面镜反射后反射光线为BM(点A,B.C,D,E,F,M在同一竖直平面内).已知∠ABE=∠FBM.若要使反射光线恰好垂直于圆柱底面射出,则需要把入射光线AB与水平线CD 的夹角∠ABC 的度数调整为 ( )
A.35° B.40° C.50° D.60°
16.如图,在△ABC中,BF 平分∠ABC,过点A作BF 的垂线.交EF于点P,交 BC 于点 E,若△PBC 面积为6cm 。△APC的面积为 则△ABP的面积为( )
A.3cm B.4cm
17.一个角的余角比它的补角的 还少40°,则这个角的度数为 度.
18.刘老师的手机密码是四位数字,请你根据下面四个条件,推断正确的密码是: 。
①6,4,3,8只有两个数字正确且位置正确;②6,0,4,7只有两个数字正确但位置都不正确;③3,5,2,9四个数字都不正确;④1,8,0,9只有三个数字正确但位置都不正确.
19.将三角板 COD 的直角顶点O 放置在直线AB 上.
(1)若按照图1的方式摆放,且∠AOC =52°,射线OE平分∠BOC,则∠DOE 的大小为 ;
(2)若按照图2 的方式摆放,射线 OE 平分 请写出∠AOC 与. 度数的等量关系,并说明理由.
冲刺满分特训
20.综合与实践 综合与实践课上,老师让同学们以“平行中的数量关系”为主题开展数学活动.已知AB∥CD,BF为∠ABE 的平分线,DF 为∠CDE 的平分线,BF 和DF 相交于点 F.
探究问题
(1)在图1中,请直接写出∠BFD,∠ABF,∠CDF 之间的数量关系,并说明理由;
(2)在图1中,∠BFD,∠ABE,∠CDE 之间的数量关系为: ;
知识迁移
(3)如图2,若. 试猜想 和 间的数量关系,并说明理由.
参考答案
考点分析
【例1】B 1.1 B
【例2】解:(1)∵AB+BC=AC,BC= ∴AC=AB+BC=21+7=28.
(2)∵O是AC的中点, ∴OB=CO-BC=14-7=7.
2.1 A
【例3】 C
3.1:(1)35.6 (2)60 (3)146°33'
【例4】 C
4.1 解:(1)∵ OD,OE 分别平分∠AOC和∠BOC,
∴ ∠COD = ∠AOC,∠COE = ∠BOC),
即 =90°.
(2)∵∠AOD=∠COD=65°,∴ ∠AOE = ∠AOD + ∠DOE =65°
(3)∵∠COD:∠COE=3:2,∴设∠COD=3x,∠COE=2x.
∵∠COD+∠COE=90°,∴3x+2x=90°,解得x=18°,
∴∠COD=54°,∴∠AOD=54°,
∴ ∠AOE = ∠AOD + ∠DOE =54°
【例5】 110° 5.1 141°
【例6】 B 6.1 A
【例7】 B
【例8】 B 8.1 B 8.2 C 8.3 D 8.4 78°
8.5 20 解析:作DG⊥BC 于 G,AH⊥BC 于 H.
∵ AD∥BC,∴AH = DG.
又∵AB∥CD,∴四边形ABCD是平行四边形,∴ BC =AD =5.
又∵ BE =8,∴CE=3.
又∵△DCE 的面积为6,∴DG=4,∴四边形ABCD 的面积=BC×AH=20.
【例9】 B
【例10】 4 10.1 C
10.2 解:由题意可知,点P 是线段AB 的垂直平分线与以点 C 为圆心、CA长为半径画弧的交点.
10.3:解:(1)∵ME 是边 AB 的垂直平分线,NF 是AC的垂直平分线,
∴BE=AE,FA=FC,∴AE+AF=BE+FC=7.
(2)∵∠B+∠C=45°,∴∠BAC=135°.
∵BE=AE,FA=FC,∴∠EAB=∠B,∠FAC=∠C,
∴∠EAB+∠FAC=45°,∴∠EAF=90°.
∵AF=4,∴AE=3,∴ △AEF 的面积
【例11】
11.1:如图所示.
【例12】 A 12.1 B 12.2 A
达标训练
1. A 2. B 3. A 4. A 5. A 6. C 7. B 8. B 12. C 13. D
14. D 解析:如图,
对于纸带①,∵∠1 = ∠2 =59°,∴ ∠1 =∠ADB = 59°,
∴∠DBA =180° - ∠ADB-∠2 =62°.由翻折的性质,得∠ABC = ∠DBA = 62°.∵ ∠2≠∠ABC,∴AD与 EC 不平行.
对于纸带②,由翻折的性质,得∠CGH= ∠DGH,∠EHG= ∠FHG.
又∵C,G,D在同一直线上,点E,H,F也在同一直线上,∴ ∠CGH +∠DGH=180°,∠EHG+∠FHG=180°,∴ ∠CGH = ∠DGH = 90°,∠EHG= ∠FHG=90°,∴ ∠CGH+∠EHG =180°,∴CD∥EF.
综上所述,纸带①的边线不平行,纸带②的边线平行.
15. C
16. C 解析:设△ABP 的面积为S cm .
∵ BF 平分∠ABC,AP⊥BF,∴BA=BE,AP=PE,∴ S△BPE
S,解得
17.30
18.0418 解析:∵3,5,2,9四个数字都不正确且1,8,0,9只有三个数字正确,∴1,8,0 三个数字都正确.
∵刘老师的手机密码是四位数字,∴剩下的4,6,7 三个数字中有且只有一个数字正确.
∵6,4,3,8只有两个数字正确且位置正确,且8正确,3不正确,∴6或4正确,假设6正确,则它的位置也正确,这与6,0,4,7只有两个数字正确但位置都不正确矛盾,∴6不正确,4正确.
∵6,4,3,8只有两个数字正确(4,8)且位置正确,1,8,0,9 只有三个数字正确(1,8,0)但位置都不正确,∴0在最前面,1在4 的后面.∴正确的密码是0418.
19.解:(1)26°.
(2)∠AOC=2∠DOE.理由如下:
∵∠AOB=180°,∠COD=90°,∴∠AOC+∠COD =∠AOC+90°
∴∠AOC--∠BOD=90°,∴2∠AOC-2∠BOD=180°①.
∵OE平分∠BOC,∴∠BOC=2∠BOE.
∵∠AOC+∠BOC=180°,∴ ∠AOC+2∠BOE=180°②.
①-②,得∠AOC-2(∠BOD +∠BOE)=0,∴∠AOC-2∠DOE=0,即∠AOC=2∠DOE.
20.解:(1)如图1 所示,过点 F 作 FG∥AB.
∵AB∥CD,∴AB∥FG∥CD,∴ ∠ABF = ∠BFG, ∠CDF=∠DFG.
∵∠BFG+∠DFG=∠BFD,∴ ∠BFD=∠ABF+∠CDF.
(2)∠ABE+∠CDE=2∠BFD.
(3)∠MDF=3∠CDM.理由如下:如图2 所示,过点 E 作 EQ∥AB,过点M作MP∥AB.
设∠CDM=x,∠ABM=y,
∵CD∥AB,∴EQ∥MP∥AB∥CD,∴ ∠CDM =∠PMD =x,∠ABM =∠PMB=y.
∵ ∠ABE + ∠QEB =180°,∠CDE+∠QED=180°,∴ ∠ABE + ∠QEB + ∠CDE +∠QED=360°,∴ ∠ABE + ∠CDE + ∠BED=360°,∴ ∠BED = 360° - ( ∠ABE +∠CDE).
∵∠E+8∠M=360°,即∠BED +8∠BMD=360°,∴ 360° - ( ∠ABE + ∠CDE) +8∠BMD=360°,∴8∠BMD=∠ABE+∠CDE.
∵ ∠BMD =∠PMD + ∠PMB =x+y,∴ 8 ∠BMD = 8x + 8y = ∠ABE+∠CDE.
∴∠EBF=4y.
∵ BF 为∠ABE 的平分线,DF 为∠CDE 的平分线,∴ ∠EBF = ∠ABF = 4y, ∠CDF=∠EDF,∴∠ABE=8y.
∵∠ABE+∠CDE=8x+8y,∴∠CDE=8x,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 三角形
第1节 几何初步认识
考点分析
考点1 直线、射线、线段
课标要求导航:
①通过实物和模型,了解从物体抽象出来的几何体、平面、直线和点等概念;
②会比较线段的长短,理解线段的和、差,以及线段中点的意义;
③掌握基本事实:两点确定一条直线;④掌握基本事实:两点之间线段最短;
⑤理解两点间距离的意义,能度量和表达两点间的距离.
例1 汽车灯所射出的光线可以近似地看成 ( )
A.线段 B.射线 C.直线 D.曲线
1.1 直线、线段、射线的位置如图所示,如图中能相交的是 ( )
例2 如图,点B 是线段AC上一点,且
(1)求线段AC的长;
(2)若点O 是线段AC 的中点,求线段OB 的长.
2.1 平面上有三点A,B,C,若AB=8,AC=5,BC=3,则 ( )
A.点 C 在线段AB 上 B.点 C 在线段AB 的延长线上
C.点 C 在线段AB 外 D.点C 可能在AB 上,也可能在AB 外
考点2 角
课标要求导航:理解角的概念,能比较角的大小;认识度、分、秒等角的度量单位,能进行简单的单位换算,会计算角的和、差.
例3 如图中用量角器测得∠ABC的度数= ( )
A.50° B.80° C.130° D.150°
3.1 角的换算.
(1)锐角54°24'的余角等于 度.
(2)若一个角的补角等于它的余角的4倍,则这个角的度数是 度.
(3)已知α与β互为补角,α=33°27′,则β= .
例4 如图,∠AOC =90°,OC 平分∠DOB,且∠DOC=22°36',∠BOA度数是 ( )
A.67°64' B.57°64' C.67°24' D.68°24'
4.1 如图,点A,O,B在同一条直线上,OD,OE 分别平分∠AOC和∠BOC.
(1)求∠DOE 的度数;
(2)如果∠COD=65°,求∠AOE 的度数;
(3)如果∠COD:∠COE=3:2,求∠AOE 的度数.
例5 一个同学从A地出发沿南偏西 方向走到B地,再从 B 地出发沿南偏东 方向走到 C 地,那么 为 .
5.1 如图,在灯塔O 处观测到轮船A位于北偏西 的方向,同时轮船B 在南偏东 的方向,那么
考点3 相交线与平行线
类型1 相交线
课标要求导航:
①理解对顶角、余角、补角等概念,探索并掌握对顶角相等、同角(或等角)的余角相等、同角(或等角)的补角相等的性质;
②理解垂线、垂线段等概念,能用三角板或量角器过一点画已知直线的垂线;
③掌握基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直;
④理解点到直线的距离的意义,能度量点到直线的距离.
例6 如图,直线AB,CD 相交于点 O.若 则 的度数为 ( )
A.70°
6.1 如图,直线AB,CD 相交于点O,OE 平分 若 则 的度数为 ( )
A.46° B.56° C.67° D.77°
例7 如图,要把河中的水引到水池A中,应在河岸 B 处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是 ( )
A.点到直线的距离 B.垂线段最短
C.两点确定一条直线 D.两点之间线段最短
类型2 平行线的性质与判定
课标要求导航:
①识别同位角、内错角、同旁内角;
②理解平行线的概念;
③掌握平行线基本事实Ⅰ:过直线外一点有且只有一条直线与这条直线平行;
④掌握平行线基本事实Ⅱ:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;
⑤探索并证明平行线的判定定理:两条直线被第三条直线所截,如果内错角相等(或同旁内角互补),那么这两条直线平行;
⑥掌握平行线的性质定理Ⅰ:两条平行直线被第三条直线所截,同位角相等.了解定理的证明;
⑦探索并证明平行线的性质定理Ⅱ:两条平行直线被第三条直线所截,内错角相等(或同旁内角互补);
⑧能用三角板和直尺过已知直线外一点画这条直线的平行线;
⑨能用尺规作图:过直线外一点作这条直线的平行线;
⑩了解平行于同一条直线的两条直线平行.
例8 一把直尺和一个含30°角的直角三角板按如图i方式放置,若∠1=20°,则∠2= ( )
A.30° B.40° C.50° D.60°
8.1 如图,AB∥CD,点 E在线段 BC上(不与点B,C重合),连接DE.若∠D=40°,∠BED=60°,则∠B= ( )
A.10° B.20° C.40° D.60°
8.2 如图,已知AD∥BC,BD 平分∠ABC.若∠A=110°,则∠D 的度数是 ( )
A.40° B.36° C.35° D.30°
8.3 已知直线a,b被c,d所截,若∠1=∠2=60°,∠3=55°,则∠4 的度数是( )
A.60° B.55° C.120° D.125°
8.4 一杆古秤在称物时的状态如图所示,已知∠1=102°,则∠2的度数为 .
8.5 如图,AB∥CD,AD∥BC,AD=5,BE=8,△DCE的面积为6,则四边形ABCD的面积为
例9 已知∠AOB,点 P 为OA上一点,用尺规作图,过点 P 作OB 的平行线.下列作图痕迹不正确的是 ( )
考点4 线段的垂直平分线、角平分线
课标要求导航:
①理解角平分线的概念,探索并证明角平分线的性质定理:角平分线上的点到角两边的距离相等;反之,角的内部到角两边距离相等的点在角的平分线上;
②理解线段垂直平分线的概念,探索并证明线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等;反之,到线段两端距离相等的点在线段的垂直平分线上;
③能用尺规作图:作一个角的平分线;
④能用尺规作图:作一条线段的垂直平分线.
例10 如图,在中,AC的垂直平分线交BC于点D,交AC于点E,若则DC的长是 .
10.1 如图,在 中, ,DE垂直平分AB交BC于点D,若 的周长为50cm,则AC+BC= ( )
A.25 cm B.45 cm C.50cm D.55 cm
【思路点拨】根据线段垂直平分线得出 ,进而利用三角形的周长解答即可.
10.2 尺规作图 在 内找一点 P,使点 P 到A,B两点的距离相等,并且点 P 到点 C 的距离等于线段AC的长.
10.3 如图,在 中,边AB 的垂直平分线分别交BC,AB于点E,M,边AC的垂直平分线分别交BC,AC于点 F,N,BE
(1)求 的长;
(2)若 求 的面积.
例11 如图,△ABC中,∠A=90°,AB=8,AC=15,以点 B 为圆心,适当长为半径画弧,分别交 BA,BC 于点 M,N,再分别以点 M,N为圆心,大于 的长为半径画弧,两弧交于点E,作射线 BE 交AC 于点 D,则线段AD 的长为 .
11.1 尺规作图 如图,△ABC 中, ,垂足为 D.求作∠ABC 的平分线,分别交AD,AC 于 P,Q 两点.(要求:尺规作图,保留作图痕迹,不写作法)
考点5 命题、定理与证明
课标要求导航:
①通过具体实例,了解定义、命题、定理、推论的意义;
②结合具体实例,会区分命题的条件和结论,了解原命题及其逆命题的概念.会识别两个互逆的命题,知道原命题成立其逆命题不一定成立;
③知道证明的意义和证明的必要性,知道数学思维要合乎逻辑,知道可以用不同的形式表述证明的过程,会用综合法的证明格式;
④了解反例的作用,知道利用反例可以判断一个命题是错误的.
例12 下列命题中,正确的是 ( )
A.两点之间,线段最短 B.菱形的对角线相等
C.正五边形的外角和为 D.直角三角形是轴对称图形
【思路点拨】根据两点之间,线段最短、菱形的性质、正多边形的外角和、轴对称图形的概念判断即可.
12.1 下列命题是真命题的是 ( )
A.同位角相等 B.菱形的四条边相等
C.正五边形是中心对称图形 D.单项式 的次数是4
12.2 对于命题“如果 ,那么 ”能说明它是假命题的反例是 ( )
达标训练
基础达标特训
1.若∠A =80°,则∠A 的补角是 ( )
A.100° B.80° C.40° D.10°
2.如图,乙地在甲地的北偏东50°方向上,则∠1 的度数为 ( )
A.60° B.50° C.40° D.30°
3.如图,在纸上画有∠AOB,将两把直尺按图示摆放,直尺边缘的交点 P在∠AOB的平分线上,则 ( )
A. 与 一定相等 B. 与 一定不相等
C. 与 一定相等 D. 与 一定不相等
4.跨学科·物理 如图,推动水桶,以点O为支点,使其向右倾斜.若在点A 处分别施加推力 F ,F ,则 F 的力臂 OA大于 F 的力臂OB.这一判断过程体现的数学依据是 ( )
A.垂线段最短 B.过一点有且只有一条直线与已知直线垂直
C.两点确定一条直线 D.过直线外一点有且只有一条直线与已知直线平行
5.如图,直线m∥n,一块含有30°的直角三角板按如图所示放置.若∠1 =40°,则∠2的大小为 ( )
A.70° B.60° C.50° D.40°
6.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB 于E,垂足为D.如果 CE=10,则ED的长为 ( )
A.3 B.4 C.5 D.6
7.如图,小明在地图上量得∠1=∠2,由此判断幸福大街与平安大街互相平行,他判断的依据是 ( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.对顶角相等
8.如图,AB∥CD,AD 平分∠BAC,∠1=30°,则∠2= ( )
A.15° B.30° C.45° D.60°
9.如图,一条公路的两侧铺设了AB,CD两条平行管道,并有纵向管道AC连通,若∠1 =120°,则∠2 的度数是 ( )
A.50° B.60° C.70° D.80°
10.如图,A,B,C,D,E,P,Q,R,S,T是构成五角星的五条线段的交点,则图中共有线
段 条.
11. 已知∠A =30°45',∠B =30. 45°,则∠A ∠B.(填“>”“<”或“=”)
高分提能特训
12.如图,两个平面镜平行放置,光线经过平面镜反射时,∠1 =∠2=40°,则∠3 的度数为 ( )
A.80° B.90° C.100° D.120°
13.如图,在△ABC 中,∠ABC A=90°,∠C=30°,以点A 为圆心,以AB 的长为半径作弧交AC于点D,连接BD,再分别以点B,D为圆心,大于 BD 的长为半径作弧,两弧交于点 P,作射线AP 交 BC于点E,连接DE,则下列结论中不正确的是 ( )
A. BE=DE B. AE=CE C. CE=2BE
14.综合与实践 如图,在一次综合实践课上,为检验纸带①、②的边线是否平行,小庆和小铁采用了两种不同的方法:小庆把纸带①沿 AB 折叠,量得∠1 =∠2=59°;小铁把纸带②沿 GH 折叠,发现GD与GC重合,HF 与HE 重合,且点 C,G,D在同一直线上,点E,H,F也在同一直线上.则下列判断正确的是( )
A.纸带①、②的边线都平行
B.纸带①、②的边线都不平行
C.纸带①的边线平行,纸带②的边线不平行
D.纸带①的边线不平行,纸带②的边线平行
15.跨学科·物理 如图,在空心圆柱口放置一面平面镜EF,EF 与水平线CD的夹角∠EBC=70°,人射光线AB经平面镜反射后反射光线为BM(点A,B.C,D,E,F,M在同一竖直平面内).已知∠ABE=∠FBM.若要使反射光线恰好垂直于圆柱底面射出,则需要把入射光线AB与水平线CD 的夹角∠ABC 的度数调整为 ( )
A.35° B.40° C.50° D.60°
16.如图,在△ABC中,BF 平分∠ABC,过点A作BF 的垂线.交EF于点P,交 BC 于点 E,若△PBC 面积为6cm 。△APC的面积为 则△ABP的面积为( )
A.3cm B.4cm
17.一个角的余角比它的补角的 还少40°,则这个角的度数为 度.
18.刘老师的手机密码是四位数字,请你根据下面四个条件,推断正确的密码是: 。
①6,4,3,8只有两个数字正确且位置正确;②6,0,4,7只有两个数字正确但位置都不正确;③3,5,2,9四个数字都不正确;④1,8,0,9只有三个数字正确但位置都不正确.
19.将三角板 COD 的直角顶点O 放置在直线AB 上.
(1)若按照图1的方式摆放,且∠AOC =52°,射线OE平分∠BOC,则∠DOE 的大小为 ;
(2)若按照图2 的方式摆放,射线 OE 平分 请写出∠AOC 与. 度数的等量关系,并说明理由.
冲刺满分特训
20.综合与实践 综合与实践课上,老师让同学们以“平行中的数量关系”为主题开展数学活动.已知AB∥CD,BF为∠ABE 的平分线,DF 为∠CDE 的平分线,BF 和DF 相交于点 F.
探究问题
(1)在图1中,请直接写出∠BFD,∠ABF,∠CDF 之间的数量关系,并说明理由;
(2)在图1中,∠BFD,∠ABE,∠CDE 之间的数量关系为: ;
知识迁移
(3)如图2,若. 试猜想 和 间的数量关系,并说明理由.
参考答案
考点分析
【例1】B 1.1 B
【例2】解:(1)∵AB+BC=AC,BC= ∴AC=AB+BC=21+7=28.
(2)∵O是AC的中点, ∴OB=CO-BC=14-7=7.
2.1 A
【例3】 C
3.1:(1)35.6 (2)60 (3)146°33'
【例4】 C
4.1 解:(1)∵ OD,OE 分别平分∠AOC和∠BOC,
∴ ∠COD = ∠AOC,∠COE = ∠BOC),
即 =90°.
(2)∵∠AOD=∠COD=65°,∴ ∠AOE = ∠AOD + ∠DOE =65°
(3)∵∠COD:∠COE=3:2,∴设∠COD=3x,∠COE=2x.
∵∠COD+∠COE=90°,∴3x+2x=90°,解得x=18°,
∴∠COD=54°,∴∠AOD=54°,
∴ ∠AOE = ∠AOD + ∠DOE =54°
【例5】 110° 5.1 141°
【例6】 B 6.1 A
【例7】 B
【例8】 B 8.1 B 8.2 C 8.3 D 8.4 78°
8.5 20 解析:作DG⊥BC 于 G,AH⊥BC 于 H.
∵ AD∥BC,∴AH = DG.
又∵AB∥CD,∴四边形ABCD是平行四边形,∴ BC =AD =5.
又∵ BE =8,∴CE=3.
又∵△DCE 的面积为6,∴DG=4,∴四边形ABCD 的面积=BC×AH=20.
【例9】 B
【例10】 4 10.1 C
10.2 解:由题意可知,点P 是线段AB 的垂直平分线与以点 C 为圆心、CA长为半径画弧的交点.
10.3:解:(1)∵ME 是边 AB 的垂直平分线,NF 是AC的垂直平分线,
∴BE=AE,FA=FC,∴AE+AF=BE+FC=7.
(2)∵∠B+∠C=45°,∴∠BAC=135°.
∵BE=AE,FA=FC,∴∠EAB=∠B,∠FAC=∠C,
∴∠EAB+∠FAC=45°,∴∠EAF=90°.
∵AF=4,∴AE=3,∴ △AEF 的面积
【例11】
11.1:如图所示.
【例12】 A 12.1 B 12.2 A
达标训练
1. A 2. B 3. A 4. A 5. A 6. C 7. B 8. B 12. C 13. D
14. D 解析:如图,
对于纸带①,∵∠1 = ∠2 =59°,∴ ∠1 =∠ADB = 59°,
∴∠DBA =180° - ∠ADB-∠2 =62°.由翻折的性质,得∠ABC = ∠DBA = 62°.∵ ∠2≠∠ABC,∴AD与 EC 不平行.
对于纸带②,由翻折的性质,得∠CGH= ∠DGH,∠EHG= ∠FHG.
又∵C,G,D在同一直线上,点E,H,F也在同一直线上,∴ ∠CGH +∠DGH=180°,∠EHG+∠FHG=180°,∴ ∠CGH = ∠DGH = 90°,∠EHG= ∠FHG=90°,∴ ∠CGH+∠EHG =180°,∴CD∥EF.
综上所述,纸带①的边线不平行,纸带②的边线平行.
15. C
16. C 解析:设△ABP 的面积为S cm .
∵ BF 平分∠ABC,AP⊥BF,∴BA=BE,AP=PE,∴ S△BPE
S,解得
17.30
18.0418 解析:∵3,5,2,9四个数字都不正确且1,8,0,9只有三个数字正确,∴1,8,0 三个数字都正确.
∵刘老师的手机密码是四位数字,∴剩下的4,6,7 三个数字中有且只有一个数字正确.
∵6,4,3,8只有两个数字正确且位置正确,且8正确,3不正确,∴6或4正确,假设6正确,则它的位置也正确,这与6,0,4,7只有两个数字正确但位置都不正确矛盾,∴6不正确,4正确.
∵6,4,3,8只有两个数字正确(4,8)且位置正确,1,8,0,9 只有三个数字正确(1,8,0)但位置都不正确,∴0在最前面,1在4 的后面.∴正确的密码是0418.
19.解:(1)26°.
(2)∠AOC=2∠DOE.理由如下:
∵∠AOB=180°,∠COD=90°,∴∠AOC+∠COD =∠AOC+90°
∴∠AOC--∠BOD=90°,∴2∠AOC-2∠BOD=180°①.
∵OE平分∠BOC,∴∠BOC=2∠BOE.
∵∠AOC+∠BOC=180°,∴ ∠AOC+2∠BOE=180°②.
①-②,得∠AOC-2(∠BOD +∠BOE)=0,∴∠AOC-2∠DOE=0,即∠AOC=2∠DOE.
20.解:(1)如图1 所示,过点 F 作 FG∥AB.
∵AB∥CD,∴AB∥FG∥CD,∴ ∠ABF = ∠BFG, ∠CDF=∠DFG.
∵∠BFG+∠DFG=∠BFD,∴ ∠BFD=∠ABF+∠CDF.
(2)∠ABE+∠CDE=2∠BFD.
(3)∠MDF=3∠CDM.理由如下:如图2 所示,过点 E 作 EQ∥AB,过点M作MP∥AB.
设∠CDM=x,∠ABM=y,
∵CD∥AB,∴EQ∥MP∥AB∥CD,∴ ∠CDM =∠PMD =x,∠ABM =∠PMB=y.
∵ ∠ABE + ∠QEB =180°,∠CDE+∠QED=180°,∴ ∠ABE + ∠QEB + ∠CDE +∠QED=360°,∴ ∠ABE + ∠CDE + ∠BED=360°,∴ ∠BED = 360° - ( ∠ABE +∠CDE).
∵∠E+8∠M=360°,即∠BED +8∠BMD=360°,∴ 360° - ( ∠ABE + ∠CDE) +8∠BMD=360°,∴8∠BMD=∠ABE+∠CDE.
∵ ∠BMD =∠PMD + ∠PMB =x+y,∴ 8 ∠BMD = 8x + 8y = ∠ABE+∠CDE.
∴∠EBF=4y.
∵ BF 为∠ABE 的平分线,DF 为∠CDE 的平分线,∴ ∠EBF = ∠ABF = 4y, ∠CDF=∠EDF,∴∠ABE=8y.
∵∠ABE+∠CDE=8x+8y,∴∠CDE=8x,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
