五四制鲁教版数学一轮复习 第四章 三角形 第2节 三角形与全等三角形(含答案)
文档属性
| 名称 | 五四制鲁教版数学一轮复习 第四章 三角形 第2节 三角形与全等三角形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 565.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-16 17:09:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第四章 三角形
第2节 三角形与全等三角形
考点分析
考点1 三角形的三边关系
课标要求导航:证明三角形的任意两边之和大于第三边.
例1 已知实数a,b,c满足 若以a,b,c为边长,能否构成三角形 若能,请求出该三角形的面积;若不能,请说明理由.
1.1 在 中,,AC 的长为奇数,的周长为 ( )
A.17 B.19 C.17或21 D.17或19
1.2 已知 的三边长为a,b,c,且a,b,c都是整数.
(1)若 且c为偶数.求 的周长;
(2)化简:.
考点2 三角形的内角和定理及其推论
课标要求导航:探索并证明三角形的内角和定理.掌握它的推论:三角形的外角等于与它不相邻的两个内角的和.
例2 如图,分别过 的顶点A,B作 若 则 的度数为 ( )
D.95
2.1 如图,在四边形 ABCD 中,CD∥AB,AC⊥BC,若∠B =50°,则∠DCA 等于( )
A.30° B.35° C.40° D.45°
2.2跨物理学科 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O 的光线相交于点 P,点F 为该凸透镜的焦点.若∠1=150°,∠3=50°,则∠2 的度数为 ( )
A.20° B.25° C.30° D.35°
考点3 三角形中重要的线段
课标要求导航:①理解三角形及其中线、高线、角平分线等概念;②探索并证明三角形的中位线定理.
例3 如图,在 Rt△ABC中,∠C=30°,D,E分别为AC,BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点 F,则四边形ABFD 的面积为 .
3.1 如图,在△ABC中,D 是 BC 边的中点,AE 是∠BAC的平分线,AE⊥CE于点E,连接DE.若AC=5,DE=1,则AB等于( )
A.7 B.6.5 C.6 D.5.5
例4 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且 则 等于 .
考点4 全等三角形的性质和判定
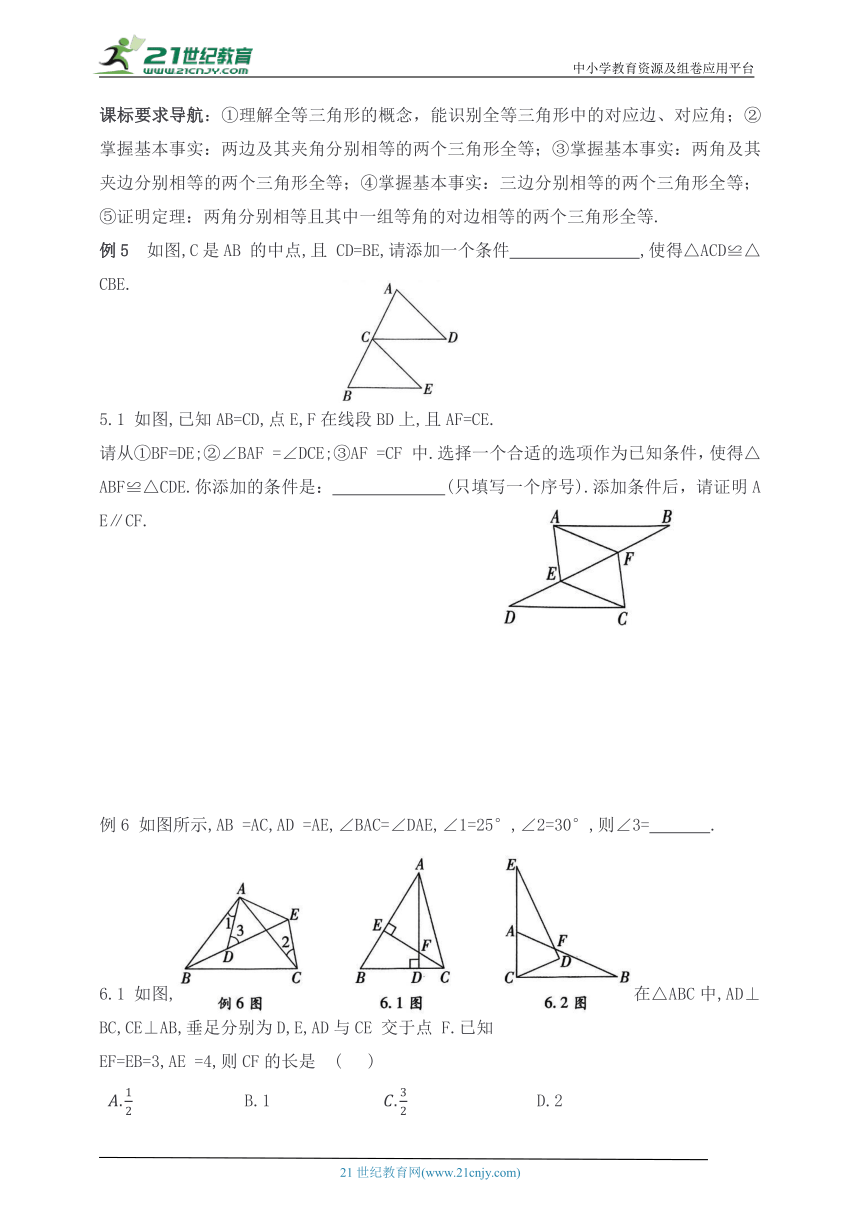
课标要求导航:①理解全等三角形的概念,能识别全等三角形中的对应边、对应角;②掌握基本事实:两边及其夹角分别相等的两个三角形全等;③掌握基本事实:两角及其夹边分别相等的两个三角形全等;④掌握基本事实:三边分别相等的两个三角形全等;⑤证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
例5 如图,C是AB 的中点,且 CD=BE,请添加一个条件 ,使得△ACD≌△CBE.
5.1 如图,已知AB=CD,点E,F在线段BD上,且AF=CE.
请从①BF=DE;②∠BAF =∠DCE;③AF =CF 中.选择一个合适的选项作为已知条件,使得△ABF≌△CDE.你添加的条件是: (只填写一个序号).添加条件后,请证明AE∥CF.
例6 如图所示,AB =AC,AD =AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
6.1 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE 交于点 F.已知
EF=EB=3,AE =4,则CF的长是 ( )
B.1 D.2
6.2 如图,△ABC≌△CED,点A 在CE边上,∠CAB+∠E=90°,ED与AB 交于点F,则下列结论不正确的是 ( )
A. DE=BC B.∠D=90° C.∠BFD+∠B=∠ACD D. EF=FB
6.3 如图,在△ABC中,CP平分∠ACB,AP⊥CP 于点P,若△ABC 的面积为,则阴影部分的面积为 .
6.4 如图,在△ACB 中,∠ACB =90°,AC =BC,点C的坐标为( -2,0),点A的坐标为( -6,3),则B点的坐标是 .
【思路点拨】过A和B分别作AD⊥OC 于D,BE⊥OC于E,利用已知条件可证明 △ADC≌△CEB,再由全等三角形的性质和已知数据即可求出B点的坐标.
考点5 全等三角形的综合应用
例7 如图,点 C 在线段AB上,AD∥EB,AC=BE,AD =BC,CF平分∠DCE.
(1)证明:△ADC≌△BCE;
(2)若CF=3,DF=4,求△DCE的面积.
7.1 综合与实践 【问题背景】
某校八年级数学社团在研究等腰三角形“三线合一”性质时发现:
①如图,在 中,若 则有
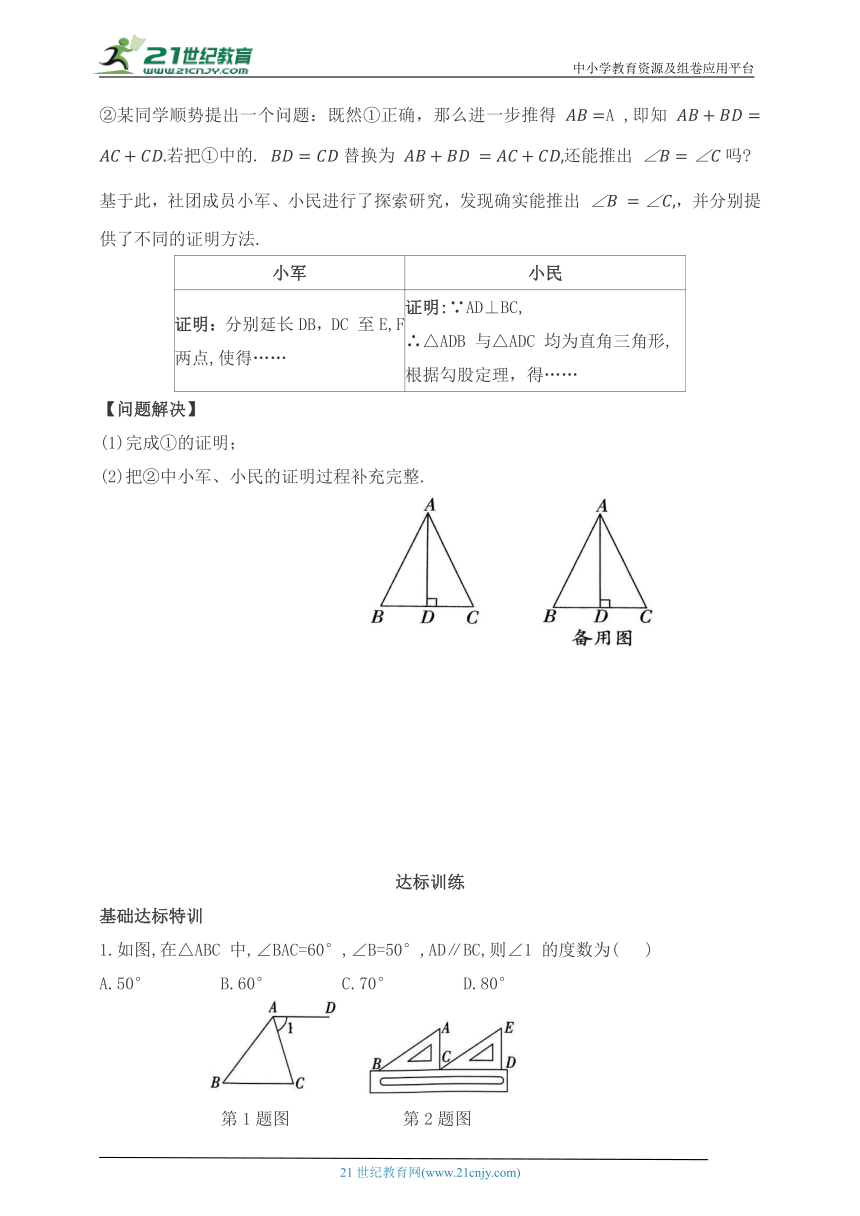
②某同学顺势提出一个问题:既然①正确,那么进一步推得 A ,即知 若把①中的. 替换为 还能推出 吗
基于此,社团成员小军、小民进行了探索研究,发现确实能推出 ,并分别提供了不同的证明方法.
小军 小民
证明:分别延长DB,DC 至E,F两点,使得…… 证明:∵AD⊥BC, ∴△ADB 与△ADC 均为直角三角形, 根据勾股定理,得……
【问题解决】
(1)完成①的证明;
(2)把②中小军、小民的证明过程补充完整.
达标训练
基础达标特训
1.如图,在△ABC 中,∠BAC=60°,∠B=50°,AD∥BC,则∠1 的度数为( )
A.50° B.60° C.70° D.80°
第1题图 第2题图
2.如图,一把直尺、两个含30°的三角尺拼接在一起,则∠ACE的度数为( )
A.120° B.90° C.60° D.30°
3.如图,AB∥CD,过点 D 作DE⊥AC 于点 E.若∠D =50°,则∠A 的度数为( )
A.130° B.140° C.150° D.160°
第3题图 第4题图
4.如图,AD∥BC,AB⊥AC,若∠1=35.8°,则∠B的度数是 ( )
A.35°48' B.55°12' C.54°12' D.54°52'
5.如图,在△ABC 中,点A的坐标为(0,1),点B 的坐标为(4,1),点 C的坐标为(3,4),点D 在第一象限(不与点C重合),且△ABD与△ABC全等,点D 的坐标是 .
第5题图 第6题图
6.如图,△ABC≌△CDE,若∠D=35°,∠ACB=45°,则∠DCE 的度数为
7.在△ABC 中,∠A =60°,AC=4.若△ABC 是锐角三角形,则边 AB 长的取值范围是 .
高分提能特训
8.如图,△ABC内部有一点D,且△DAB,△DBC,△DCA 的面积分别为5,4,3.若△ABC 的重心为G,则下列叙述何者正确 ( )
A.△GBC 与△DBC 的面积相同,且 DG 与BC平行
B.△GBC 与△DBC 的面积相同,且 DG 与BC不平行
C.△GCA与△DCA的面积相同,且DG与AC平行
D.△GCA与△DCA的面积相同,且DG与AC不平行
9.新定义 如图1,△ABC与△A B C 满足∠A=∠A ,AC=A C ,BC=B C ,∠C≠∠C ,我们称这样的两个三角形为“伪全等三角形”.如图2,在△ABC中,AB=AC,点D,E在线段BC上,且BE=CD,则图中共有“伪全等三角形”( )
A.1对 B.2对 C.3对 D.4对
10.如图,在△ABC 中,∠B =50°,∠C=30°,AD 是高,以点A 为圆心,AB长为半径画弧,交AC于点E,再分别以B,E为圆心,大于 BE的长为半径画弧,两弧在∠BAC 的内部交于点F,作射线AF,则∠DAF= °.
11.在等边△ABC三边上分别取点D,E,F,使得AD=BE=CF,连接三点得到△DEF,易得△ADF≌△BED≌△CFE,设S△ABC=1,则
如图①,当 时,
如图②,当 时。 ;
如图③,当 时, ……
直接写出,当 时,.
12.如图,B,E,C,F是直线l上的四点,AC,DE 相交于点 G,AB =DF,AC=DE,BC=EF.
(1)求证:△GEC是等腰三角形;
(2)连接AD,则 AD 与l 的位置关系是
冲刺满分特训
13.综合与实践 如图1,在△ABC中,BD 是∠ABC 的平分线,BD 的延长线交外角∠CAM的平分线于点E.
【发现结论】
结论1:∠AEB= ∠ACB= .
结论2:当图1中∠ACB±90°时,如图2所示,延长BC交AE于点F,过点E作AF的重线交BF于点G,交AC的延长线于点H.则AE 与EG的数量关系是 .
【应用结论】
(1)求证:AH=GF;
(2)在图2中连接PH,AG,延长AG交FH于点N,补全图形,求证:
参考答案
考点分析
【例1】解:∵a,b,c满足|
∴能构成三角形.
∵20+5=25,∴此三角形是直角三角形,
∴三角形的面积
1.1:D
1.2:解:(1)∵a=2,b=5,∴5-2∵c为偶数,∴c=4或6.
当c=4时,△ABC的周长=a+b+c=2+5+4=11;
当c=6时,△ABC的周长=a+b+.c=2+5+6=13.
综上所述,△ABC 的周长为11或13.
(2)∵△ABC的边长为a,b,c,∴a+c>b,∴|a-b+c|-|b-c-a|+|a+b+ cl=a+c-b-(a+c-b)+a+b+c=a+c-b-a-c+b+a+b+c=a+b+c.
【例2】 B 2.1:C 2.2:A
【例3】8 3.1:A
=【例4】 解析:∵点D,E,F分别为边BC,AD,CE的中点,∴AD,CE,DF分别是△ABC,△ACD,△CDE 的中线,
【例5】AD=CE(答案不唯一)
5.1:解:①(或②).
若选择①BF=DE.
证明:在△ABF和△CDE中,∴△ABF≌△CDE(SSS),∴∠B=∠D.
∵BF=DE,∴ BF +EF =DE +EF,即 BE=DF.
在△ABE 和△CDF中, ∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,∴AE∥CF.
若选择②∠BAF=∠DCE.
证明:在△ABF 和△CDE中, ∴△ABF≌△CDE(SAS),
∴∠B=∠D,DE=BF.
同理可证△ABE≌△CDF(SAS),∴∠AEB=∠CFD,∴AE∥CF.
【例6】55° 6.1:B 6.2:D
6.3:3 解析:延长AP 交 BC 于 D,
∵CP平分∠ACB,∴ ∠ACP = B∠DCP.
∵ AP ⊥ CP,∴ ∠APC =∠DPC = 90°.
在 △ACP 与△DCP中, ACP ≌△DCP(ASA),∴ AP =DP,
∴ S△ABP 阴影部分的面积
6.4:(1,4) 解析:过点A 和点 B 分别作AD⊥OC于D,BE⊥OC于E.
∵∠ACB=90°,∴ ∠ACD +∠CAD=90°,∠ACD +∠BCE =90°,∴∠CAD = ∠BCE. 在 △ADC 和△CEB中 ∴△ADC≌△CEB(AAS),
∴ DC =BE,AD = CE.
∵ 点 C 的坐标为(-2,0),点A 的坐标为( - 6,3),∴OC=2,AD=CE=3,OD=6,
∴CD=OD--OC=4,OE=CE-OC =3-2=1,∴BE =4,∴B 点的坐标是(1,4).
【例7】解:(1)证明:∵AD∥BE,∴∠A=∠B.
在△ACD 和△BEC中, ∴△ACD≌△BEC(SAS).
(2)由(1)知△ADC≌△BCE,∴DC=CE.
又∵CF平分∠DCE,∴CF⊥DE,DF=EF,∴ CF 垂直平分DE.
∵CF=3,DF=4.∴DE=2DF=8, 即△DCE的面积是12.
7.1:解:(1)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°.
在△ADB 和△ADC 中, . ∴△ADB≌△ADC(SAS),
∴∠B=∠C.
(2)小军的证明过程:
分别延长DB,DC至 E,F两点,使得BE=BA,CF=CA,如图所示.
∵AB+BD=AC+CD,∴BE+BD=CF+CD,∴DE=DF.
∵AD⊥BC,∴∠ADE=∠ADF=90°.
在△ADE 和△ADF中,∴△ADE≌△ADF(SAS),∴∠E=∠F.
∵BE=BA,CF=CA,∴∠E=∠BAE,∠F=∠CAF.
∵ ∠ABC =∠E +∠BAE,∠ACB =∠F+∠CAF,∴∠ABC=∠ACB.
小民的证明过程:
∵AD⊥BC,∴ △ADB 与△ADC 均为直角三角形.
根据勾股定理,得
又
达标训练
1. C 2. C 3. B 4. C 5.(1,4) 6.100°
7. 解析:已知△ABC中,∠A= 60°,AC = 4. 如图,
当 CB ⊥AB 时,此时 AB 最短, 当B C⊥AC时,此时AB最长, 2AC=8.所以边AB长的取值范围是28. A 解析:∵ △ABC内部有一点D,且△DAB,△DBC,△DCA的面积分别为5,4,3,∴S△ABC=5 +4+3 =12.∵ △ABC 的重心为 G,∴S△GBC S△DBC=4,∴ 点 D,G到 BC 的距离相等,且位于 BC 的同侧,∴DG∥BC,故结论 A 正确,结论 B,C,D错误.
9. D 解析:∵AB=AC,∴∠B =∠C.
在△ABE 和 △ACD 中,∴△ABE≌△ACD(SAS),∴AD=AE.
∵AB=AB,∠B=∠B,AD=AE,∠BAD≠∠BAE,∴△ABD和△ABE是一对“伪全等三角形”.同理可得,△ABD 和△ACD 是一对“伪全等三角形”. △ACD 和△ACE 是一对“伪全等三角形”.△ABE 和△ACE 是一对“伪全等三角形”.所以图中的“伪全等三角形”共有4对.
10. 10
解析:由题可知,当 时, ∴当 时,
12.解:(1)证明:在△ABC和△DFE中,∴△ABC≌△DFE(SSS),
即∠GCE=∠GEC,∴ △GEC为等腰三角形.
(2)AD∥.
13.解:【发现结论】结论1:
结论2:AE=EG.
【应用结论】
(1)证明:在 Rt△AFC 中,∠EFG+ ∠EAH =90°,
在 Rt△AEH 中,∠AHE+∠EAH=90°,∴ ∠EFG=∠EHA.
在△EFG和△EHA中,∴ △EFG△EHA(AAS),∴AH=GF.
(2)补全图形如图所示.
证明:在Rt△AEG中,∵∠EAG=∠EGA=45°,
∵Rt△EFG≌Rt△EHA,∴ EF=EH.
∵∠FEH=90°,∴∠EFH=∠EHF=45°,∴∠AFN=∠FAN=45°,∠NGH=∠AGE=45°,
∴ FN=AN,∠NGH=∠NHG=45°,∴ GN=HN.
又∵AN=AG+GN,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 三角形
第2节 三角形与全等三角形
考点分析
考点1 三角形的三边关系
课标要求导航:证明三角形的任意两边之和大于第三边.
例1 已知实数a,b,c满足 若以a,b,c为边长,能否构成三角形 若能,请求出该三角形的面积;若不能,请说明理由.
1.1 在 中,,AC 的长为奇数,的周长为 ( )
A.17 B.19 C.17或21 D.17或19
1.2 已知 的三边长为a,b,c,且a,b,c都是整数.
(1)若 且c为偶数.求 的周长;
(2)化简:.
考点2 三角形的内角和定理及其推论
课标要求导航:探索并证明三角形的内角和定理.掌握它的推论:三角形的外角等于与它不相邻的两个内角的和.
例2 如图,分别过 的顶点A,B作 若 则 的度数为 ( )
D.95
2.1 如图,在四边形 ABCD 中,CD∥AB,AC⊥BC,若∠B =50°,则∠DCA 等于( )
A.30° B.35° C.40° D.45°
2.2跨物理学科 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O 的光线相交于点 P,点F 为该凸透镜的焦点.若∠1=150°,∠3=50°,则∠2 的度数为 ( )
A.20° B.25° C.30° D.35°
考点3 三角形中重要的线段
课标要求导航:①理解三角形及其中线、高线、角平分线等概念;②探索并证明三角形的中位线定理.
例3 如图,在 Rt△ABC中,∠C=30°,D,E分别为AC,BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点 F,则四边形ABFD 的面积为 .
3.1 如图,在△ABC中,D 是 BC 边的中点,AE 是∠BAC的平分线,AE⊥CE于点E,连接DE.若AC=5,DE=1,则AB等于( )
A.7 B.6.5 C.6 D.5.5
例4 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且 则 等于 .
考点4 全等三角形的性质和判定
课标要求导航:①理解全等三角形的概念,能识别全等三角形中的对应边、对应角;②掌握基本事实:两边及其夹角分别相等的两个三角形全等;③掌握基本事实:两角及其夹边分别相等的两个三角形全等;④掌握基本事实:三边分别相等的两个三角形全等;⑤证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
例5 如图,C是AB 的中点,且 CD=BE,请添加一个条件 ,使得△ACD≌△CBE.
5.1 如图,已知AB=CD,点E,F在线段BD上,且AF=CE.
请从①BF=DE;②∠BAF =∠DCE;③AF =CF 中.选择一个合适的选项作为已知条件,使得△ABF≌△CDE.你添加的条件是: (只填写一个序号).添加条件后,请证明AE∥CF.
例6 如图所示,AB =AC,AD =AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
6.1 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE 交于点 F.已知
EF=EB=3,AE =4,则CF的长是 ( )
B.1 D.2
6.2 如图,△ABC≌△CED,点A 在CE边上,∠CAB+∠E=90°,ED与AB 交于点F,则下列结论不正确的是 ( )
A. DE=BC B.∠D=90° C.∠BFD+∠B=∠ACD D. EF=FB
6.3 如图,在△ABC中,CP平分∠ACB,AP⊥CP 于点P,若△ABC 的面积为,则阴影部分的面积为 .
6.4 如图,在△ACB 中,∠ACB =90°,AC =BC,点C的坐标为( -2,0),点A的坐标为( -6,3),则B点的坐标是 .
【思路点拨】过A和B分别作AD⊥OC 于D,BE⊥OC于E,利用已知条件可证明 △ADC≌△CEB,再由全等三角形的性质和已知数据即可求出B点的坐标.
考点5 全等三角形的综合应用
例7 如图,点 C 在线段AB上,AD∥EB,AC=BE,AD =BC,CF平分∠DCE.
(1)证明:△ADC≌△BCE;
(2)若CF=3,DF=4,求△DCE的面积.
7.1 综合与实践 【问题背景】
某校八年级数学社团在研究等腰三角形“三线合一”性质时发现:
①如图,在 中,若 则有
②某同学顺势提出一个问题:既然①正确,那么进一步推得 A ,即知 若把①中的. 替换为 还能推出 吗
基于此,社团成员小军、小民进行了探索研究,发现确实能推出 ,并分别提供了不同的证明方法.
小军 小民
证明:分别延长DB,DC 至E,F两点,使得…… 证明:∵AD⊥BC, ∴△ADB 与△ADC 均为直角三角形, 根据勾股定理,得……
【问题解决】
(1)完成①的证明;
(2)把②中小军、小民的证明过程补充完整.
达标训练
基础达标特训
1.如图,在△ABC 中,∠BAC=60°,∠B=50°,AD∥BC,则∠1 的度数为( )
A.50° B.60° C.70° D.80°
第1题图 第2题图
2.如图,一把直尺、两个含30°的三角尺拼接在一起,则∠ACE的度数为( )
A.120° B.90° C.60° D.30°
3.如图,AB∥CD,过点 D 作DE⊥AC 于点 E.若∠D =50°,则∠A 的度数为( )
A.130° B.140° C.150° D.160°
第3题图 第4题图
4.如图,AD∥BC,AB⊥AC,若∠1=35.8°,则∠B的度数是 ( )
A.35°48' B.55°12' C.54°12' D.54°52'
5.如图,在△ABC 中,点A的坐标为(0,1),点B 的坐标为(4,1),点 C的坐标为(3,4),点D 在第一象限(不与点C重合),且△ABD与△ABC全等,点D 的坐标是 .
第5题图 第6题图
6.如图,△ABC≌△CDE,若∠D=35°,∠ACB=45°,则∠DCE 的度数为
7.在△ABC 中,∠A =60°,AC=4.若△ABC 是锐角三角形,则边 AB 长的取值范围是 .
高分提能特训
8.如图,△ABC内部有一点D,且△DAB,△DBC,△DCA 的面积分别为5,4,3.若△ABC 的重心为G,则下列叙述何者正确 ( )
A.△GBC 与△DBC 的面积相同,且 DG 与BC平行
B.△GBC 与△DBC 的面积相同,且 DG 与BC不平行
C.△GCA与△DCA的面积相同,且DG与AC平行
D.△GCA与△DCA的面积相同,且DG与AC不平行
9.新定义 如图1,△ABC与△A B C 满足∠A=∠A ,AC=A C ,BC=B C ,∠C≠∠C ,我们称这样的两个三角形为“伪全等三角形”.如图2,在△ABC中,AB=AC,点D,E在线段BC上,且BE=CD,则图中共有“伪全等三角形”( )
A.1对 B.2对 C.3对 D.4对
10.如图,在△ABC 中,∠B =50°,∠C=30°,AD 是高,以点A 为圆心,AB长为半径画弧,交AC于点E,再分别以B,E为圆心,大于 BE的长为半径画弧,两弧在∠BAC 的内部交于点F,作射线AF,则∠DAF= °.
11.在等边△ABC三边上分别取点D,E,F,使得AD=BE=CF,连接三点得到△DEF,易得△ADF≌△BED≌△CFE,设S△ABC=1,则
如图①,当 时,
如图②,当 时。 ;
如图③,当 时, ……
直接写出,当 时,.
12.如图,B,E,C,F是直线l上的四点,AC,DE 相交于点 G,AB =DF,AC=DE,BC=EF.
(1)求证:△GEC是等腰三角形;
(2)连接AD,则 AD 与l 的位置关系是
冲刺满分特训
13.综合与实践 如图1,在△ABC中,BD 是∠ABC 的平分线,BD 的延长线交外角∠CAM的平分线于点E.
【发现结论】
结论1:∠AEB= ∠ACB= .
结论2:当图1中∠ACB±90°时,如图2所示,延长BC交AE于点F,过点E作AF的重线交BF于点G,交AC的延长线于点H.则AE 与EG的数量关系是 .
【应用结论】
(1)求证:AH=GF;
(2)在图2中连接PH,AG,延长AG交FH于点N,补全图形,求证:
参考答案
考点分析
【例1】解:∵a,b,c满足|
∴能构成三角形.
∵20+5=25,∴此三角形是直角三角形,
∴三角形的面积
1.1:D
1.2:解:(1)∵a=2,b=5,∴5-2
当c=4时,△ABC的周长=a+b+c=2+5+4=11;
当c=6时,△ABC的周长=a+b+.c=2+5+6=13.
综上所述,△ABC 的周长为11或13.
(2)∵△ABC的边长为a,b,c,∴a+c>b,∴|a-b+c|-|b-c-a|+|a+b+ cl=a+c-b-(a+c-b)+a+b+c=a+c-b-a-c+b+a+b+c=a+b+c.
【例2】 B 2.1:C 2.2:A
【例3】8 3.1:A
=【例4】 解析:∵点D,E,F分别为边BC,AD,CE的中点,∴AD,CE,DF分别是△ABC,△ACD,△CDE 的中线,
【例5】AD=CE(答案不唯一)
5.1:解:①(或②).
若选择①BF=DE.
证明:在△ABF和△CDE中,∴△ABF≌△CDE(SSS),∴∠B=∠D.
∵BF=DE,∴ BF +EF =DE +EF,即 BE=DF.
在△ABE 和△CDF中, ∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,∴AE∥CF.
若选择②∠BAF=∠DCE.
证明:在△ABF 和△CDE中, ∴△ABF≌△CDE(SAS),
∴∠B=∠D,DE=BF.
同理可证△ABE≌△CDF(SAS),∴∠AEB=∠CFD,∴AE∥CF.
【例6】55° 6.1:B 6.2:D
6.3:3 解析:延长AP 交 BC 于 D,
∵CP平分∠ACB,∴ ∠ACP = B∠DCP.
∵ AP ⊥ CP,∴ ∠APC =∠DPC = 90°.
在 △ACP 与△DCP中, ACP ≌△DCP(ASA),∴ AP =DP,
∴ S△ABP 阴影部分的面积
6.4:(1,4) 解析:过点A 和点 B 分别作AD⊥OC于D,BE⊥OC于E.
∵∠ACB=90°,∴ ∠ACD +∠CAD=90°,∠ACD +∠BCE =90°,∴∠CAD = ∠BCE. 在 △ADC 和△CEB中 ∴△ADC≌△CEB(AAS),
∴ DC =BE,AD = CE.
∵ 点 C 的坐标为(-2,0),点A 的坐标为( - 6,3),∴OC=2,AD=CE=3,OD=6,
∴CD=OD--OC=4,OE=CE-OC =3-2=1,∴BE =4,∴B 点的坐标是(1,4).
【例7】解:(1)证明:∵AD∥BE,∴∠A=∠B.
在△ACD 和△BEC中, ∴△ACD≌△BEC(SAS).
(2)由(1)知△ADC≌△BCE,∴DC=CE.
又∵CF平分∠DCE,∴CF⊥DE,DF=EF,∴ CF 垂直平分DE.
∵CF=3,DF=4.∴DE=2DF=8, 即△DCE的面积是12.
7.1:解:(1)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°.
在△ADB 和△ADC 中, . ∴△ADB≌△ADC(SAS),
∴∠B=∠C.
(2)小军的证明过程:
分别延长DB,DC至 E,F两点,使得BE=BA,CF=CA,如图所示.
∵AB+BD=AC+CD,∴BE+BD=CF+CD,∴DE=DF.
∵AD⊥BC,∴∠ADE=∠ADF=90°.
在△ADE 和△ADF中,∴△ADE≌△ADF(SAS),∴∠E=∠F.
∵BE=BA,CF=CA,∴∠E=∠BAE,∠F=∠CAF.
∵ ∠ABC =∠E +∠BAE,∠ACB =∠F+∠CAF,∴∠ABC=∠ACB.
小民的证明过程:
∵AD⊥BC,∴ △ADB 与△ADC 均为直角三角形.
根据勾股定理,得
又
达标训练
1. C 2. C 3. B 4. C 5.(1,4) 6.100°
7. 解析:已知△ABC中,∠A= 60°,AC = 4. 如图,
当 CB ⊥AB 时,此时 AB 最短, 当B C⊥AC时,此时AB最长, 2AC=8.所以边AB长的取值范围是2
9. D 解析:∵AB=AC,∴∠B =∠C.
在△ABE 和 △ACD 中,∴△ABE≌△ACD(SAS),∴AD=AE.
∵AB=AB,∠B=∠B,AD=AE,∠BAD≠∠BAE,∴△ABD和△ABE是一对“伪全等三角形”.同理可得,△ABD 和△ACD 是一对“伪全等三角形”. △ACD 和△ACE 是一对“伪全等三角形”.△ABE 和△ACE 是一对“伪全等三角形”.所以图中的“伪全等三角形”共有4对.
10. 10
解析:由题可知,当 时, ∴当 时,
12.解:(1)证明:在△ABC和△DFE中,∴△ABC≌△DFE(SSS),
即∠GCE=∠GEC,∴ △GEC为等腰三角形.
(2)AD∥.
13.解:【发现结论】结论1:
结论2:AE=EG.
【应用结论】
(1)证明:在 Rt△AFC 中,∠EFG+ ∠EAH =90°,
在 Rt△AEH 中,∠AHE+∠EAH=90°,∴ ∠EFG=∠EHA.
在△EFG和△EHA中,∴ △EFG△EHA(AAS),∴AH=GF.
(2)补全图形如图所示.
证明:在Rt△AEG中,∵∠EAG=∠EGA=45°,
∵Rt△EFG≌Rt△EHA,∴ EF=EH.
∵∠FEH=90°,∴∠EFH=∠EHF=45°,∴∠AFN=∠FAN=45°,∠NGH=∠AGE=45°,
∴ FN=AN,∠NGH=∠NHG=45°,∴ GN=HN.
又∵AN=AG+GN,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
