五四制鲁教版数学一轮复习 第四章 三角形 第5节 相似三角形(含答案)
文档属性
| 名称 | 五四制鲁教版数学一轮复习 第四章 三角形 第5节 相似三角形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 736.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-16 17:15:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第四章 三角形
第5节 相似三角形
考点分析
考点1 比例线段及其性质
课标要求导航:①了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割.②通过具体实例认识图形的相似.
例1(教材改编)下列四组线段中,不是成比例线段的是 ( )
1.1已知一个三角形的三边长分别为4,5,6,如果它与另一个三角形相似,那么另一个三角形的三边长可能是 ( )
A.2,3,4 B.8,10,12 C.12,15,20 D.15,20,30
1.2如图,点 P 把线段AB 分成两部分,且BP,AP,AB,BP是成比例线段.如果. 那么
考点2 平行线分线段成比例
课标要求导航:掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
例2 如图,在 中,D,E 分别为AB,AC上的点,连接DE,若 则 ( )
例2图 2.1图
2.1跨音乐学科 五线谱是一种记谱法,通过在五根等距离的平行横线上标以不同时值的音符及其他记号来记载音乐.如图,A,B,C为直线l与五线谱的横线相交的三个点,则 的值是 .
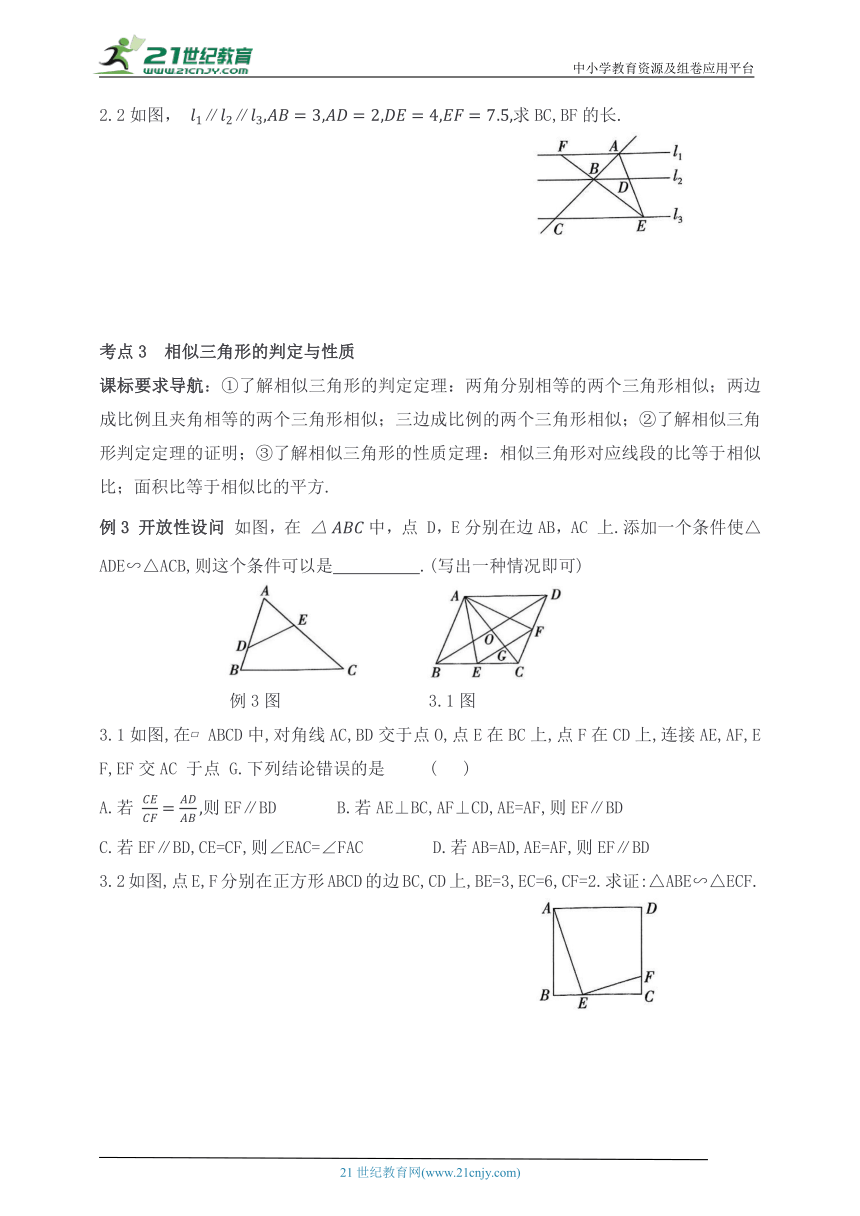
2.2如图, ∥∥求BC,BF的长.
考点3 相似三角形的判定与性质
课标要求导航:①了解相似三角形的判定定理:两角分别相等的两个三角形相似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似;②了解相似三角形判定定理的证明;③了解相似三角形的性质定理:相似三角形对应线段的比等于相似比;面积比等于相似比的平方.
例3 开放性设问 如图,在 中,点 D,E分别在边AB,AC 上.添加一个条件使△ADE∽△ACB,则这个条件可以是 .(写出一种情况即可)
例3图 3.1图
3.1如图,在 ABCD中,对角线AC,BD交于点O,点E在BC上,点F在CD上,连接AE,AF,EF,EF交AC 于点 G.下列结论错误的是 ( )
A.若 则EF∥BD B.若AE⊥BC,AF⊥CD,AE=AF,则EF∥BD
C.若EF∥BD,CE=CF,则∠EAC=∠FAC D.若AB=AD,AE=AF,则EF∥BD
3.2如图,点E,F分别在正方形ABCD的边BC,CD上,BE=3,EC=6,CF=2.求证:△ABE∽△ECF.
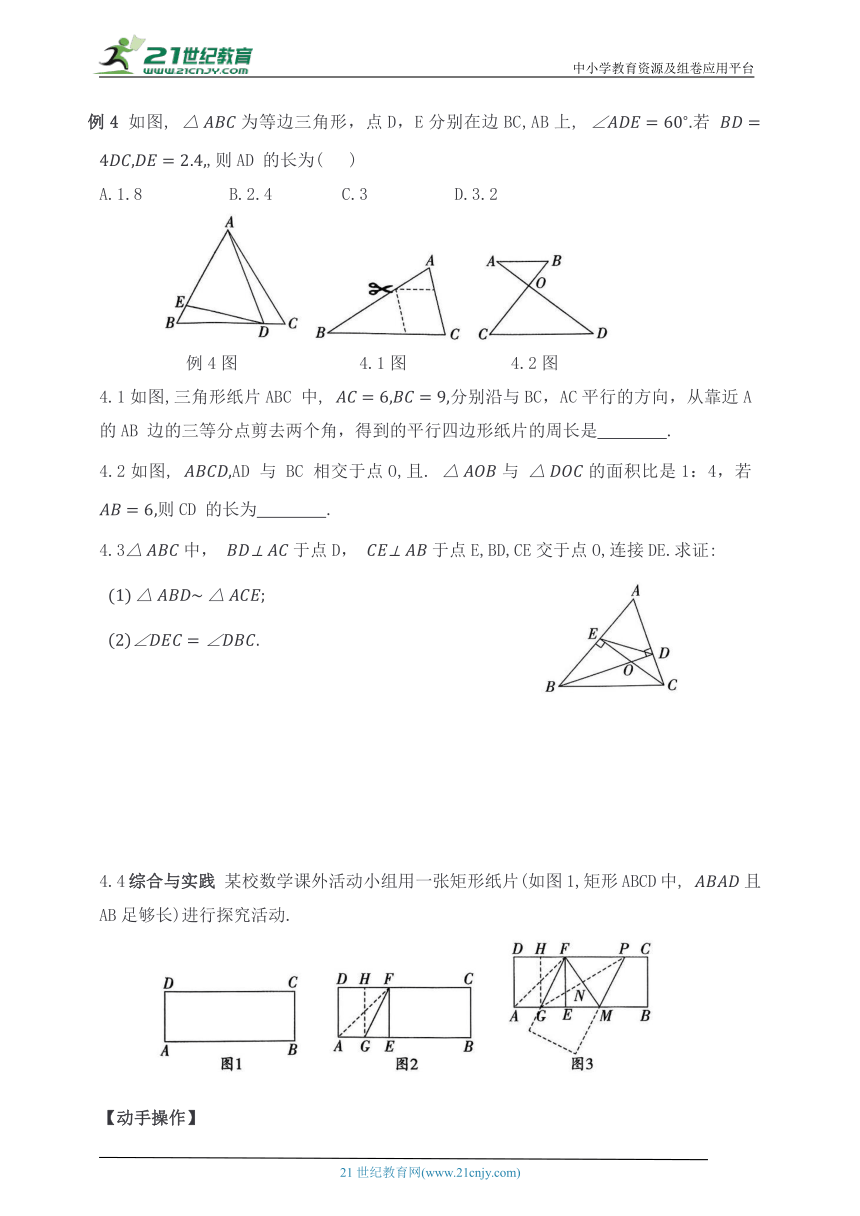
例4 如图, 为等边三角形,点D,E分别在边BC,AB上, 若 ,则AD 的长为( )
A.1.8 B.2.4 C.3 D.3.2
例4图 4.1图 4.2图
4.1如图,三角形纸片ABC 中, 分别沿与BC,AC平行的方向,从靠近A 的AB 边的三等分点剪去两个角,得到的平行四边形纸片的周长是 .
4.2如图, AD 与 BC 相交于点O,且. 与 的面积比是1:4,若 则CD 的长为 .
4.3中, 于点D, 于点E,BD,CE交于点O,连接DE.求证:
4.4综合与实践 某校数学课外活动小组用一张矩形纸片(如图1,矩形ABCD中, 且AB足够长)进行探究活动.
【动手操作】
如图2,第一步,沿点A 所在直线折叠,使点D 落在AB上的点E处,折痕为AF,连接EF,把纸片展平.
第二步,把四边形AEFD 折叠,使点A 与点 E 重合,点D 与点 F 重合,折痕为GH,再把纸片展平.
第三步,连接GF.
【探究发现】
根据以上操作,甲、乙两同学分别写出了一个结论.
甲同学的结论:四边形 AEFD 是正方形.
乙同学的结论:
(1)请分别判断甲、乙两同学的结论是否正确.若正确,写出证明过程;若不正确,请说明理由.
【继续探究】
在上面操作的基础上,丙同学继续操作.
如图3,第四步,沿点G 所在直线折叠,使点F落在AB上的点M处,折痕为GP,连接PM,把纸片展平.
第五步,连接 FM 交 GP 于点 N.
根据以上操作,丁同学写出了一个正确结论:
(2)请证明这个结论.
考点4 相似多边形
例5 已知矩形ABCD 中, ,在 BC上取一点 E,将 沿AE向上折叠,使点B 落在AD上的点 F 处.若四边形 EFDC 与矩形 ABCD相似,则
例5图 5.1图
5.1 如图,四边形ABCD和四边形EFGH 相似,且顶点都在方格纸的格点上,它们的相似比是 ( )
A.1:2 B.1:4 C.2:1 D.4:1
考点5 相似三角形的应用
课标要求导航:会利用图形的相似解决一些简单的实际问题.
例6 跨物理学科 物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图,燃烧的蜡烛(竖直放置)AB 经小孔 O 在屏幕(竖直放置)上成像. 设 小孔O到AB 的距离为30cm,则小孔O到 的距离为 cm.
【思路点拨】利用已知得出. ,进而利用相似三角形的性质求出即可.
6.1图1是伸缩折叠不锈钢晾衣架的实物图,图2是它的侧面示意图,AD 与 CB 相交于点 O, 根据图2中的数据可得x的值为 ( )
A.0.8 B.0.72 C.1.8 D.2
6.1图 6.2图
6.2数学文化 我国古代数学著作《九章算术》中的“井深”问题:“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何 ”,它的题意是:如图尺,尺,问井深BD是 ( )
A.1.25尺 B.56.5尺 C.6.25尺 D.57.5尺
达标训练
基础达标特训
1.已知一个三角形的三边长分别为4,5,6,如果它与另一个三角形相似,那么另一个三角形的三边长可能是 ( )
A.2,3,4 B.8,10,12 C.12,15,20 D.15,20,30
2.若两个相似三角形的相似比是1:3,则这两个相似三角形的面积比是( )
A.1:3 B.1:4 C.1:6 D.1:9
3.下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为 ( )
A.甲和乙 B.乙和丁 C.甲和丙 D.甲和丁
4.如图,在 ABCD 中,对角线AC,BD 相交于点 O,点 E 为 OC 的中点,EF∥AB交BC于点F.若AB=4,则 EF的长为 ( )
A. B.1 C. D.2
5.如图,矩形OABC 各顶点的坐标分别为O(0,0),A(3,0),B(3,2),C(0,2),以原点O 为位似中心,将这个矩形按相似比 缩小,则顶点B在第一象限对应点的坐标是 ( )
A.(9,4) B.(4,9) C.(1, ) D.(1, )
6.宽与长的比是 的矩形叫黄金矩形,黄金矩形给我们以协调的美感,世界各国许多著名建筑为取得最佳的视觉效果,都采用了黄金矩形的设计.已知四边形ABCD 是黄金矩形(ABA.3 B.2 C.1 D.0
7.开放性设问 (2024 青海中考)如图,AC 和BD 相交于点O,请你添加一个条件 ,使得△AOB∽△COD.
8.)如图,AB 与 CD 交于点O,且AC∥BD.若 则
9.如图所示,四边形ABCD,DEFG,GHIJ 均为正方形,且 则正方形 DEFG的边长可以是 .(写出一个答案即可)
10.如图,在 Rt△ABC 中,∠ACB =90°,D 为边AB上一点,且 CD =CA,过点 D 作 DE⊥AB交BC 于点E.求证:△CDE∽△CBD.
高分提能特训
11.如图,是用12个相似的直角三角形组成的图案.若OA=1,则OG= ( )
C.
第11题图 第12题图
12.如图,在直角坐标系中,每个网格小正方形的边长均为1 个单位长度,以点 P 为位似中心作正方形PA A A ,正方形PA A A ,…,按此规律作下去,所作正方形的顶点均在格点上,其中正方形 PA A A 的顶点坐标分别为P( - 3,0),A (-2,1),A (-1,0),A (-2,-1),则顶点A 的坐标为 ( )
A.(31,34) B.(31,-34) C.(32,35) D.(32,0)
13.如图,在△ABC 中,延长AC至点D,使CD=CA,过点D 作DE∥CB,且 DE = DC,连接 AE 交 BC 于点 F. 若∠CAB=∠CFA,CF=1,则BF= .
第13题图 第14题图
14.如图,正五边形ABCDE 的边长为4,则这个正五边形的对角线AC 的长是 .
15.如图,△ABC中,A,B两个顶点在x轴的上方,点C 的坐标是(-1,0).以点 C 为位似中心,在x轴的下方作△ABC 的位似图形△A'B'C,并把△ABC 的边长放大到原来的2倍.设B'的坐标是(3,-1),则点 B 的坐标是 .
第15题图 第16题图
16.如图,△ABC中,AB=AC,∠BAC=90°,AD 是△ABC 的角平分线.
(1)以点 B 为圆心,适当长为半径画弧,分别交 BA,BC于点 E,F.
(2)以点A 为圆心,BE 长为半径画弧,交AC 于点 G.
(3)以点 G 为圆心,EF 长为半径画弧,与
(2)中所画的弧相交于点 H.
(4)画射线AH.
(5)以点B为圆心.,BC长为半径画弧,交射线AH于点 M.
(6)连接MC,MB. MB 分别交 AC,AD 于点N,P.
根据以上信息,下面五个结论中正确的是 .(只填序号)
①BD = CD;②∠ABM = 15°;③∠APN =∠ANP;④AMAD= ;⑤MC =MN·MB.
17.如图,在菱形 ABCD中,∠ABC =60°,对角线 AC 与 BD 相交于点O,点 F 为BC的中点,连接AF与BD相交于点E,连接CE 并延长交AB于点G.证明:△BEF∽△BCO.
冲刺满分特训
18.综合与实践 为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长 EF 恰好等于自己的身高 DE.此时,小组同学测得旗杆 AB 的影长 BC 为11.3m ,据此可得旗杆高度为 m;
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部
A.小组同学测得小李的眼睛距地面高度DE=1.5m ,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16 m.求旗杆高度;
(3)小王所在小组采用图3 的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P 处,用细线系小重物Q,标高线 PQ 始终垂直于水平地面.
如图6,在江姐故里广场上E 点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA 与标高线交点 C,测得标高 CG =1.8 m,DG =1.5m .将观测点 D 后移24 m到D'处.采用同样方法,测得C'G'=1. 2m,D'G'=2m.求雕塑高度(结果精确到1m).
参考答案
【例1】C 1.1:B 1.2:
【例2】B 2.1:2
2.2:解:∵∥∥
∵AB=3,AD=2,DE=4,解得BC=6.
∵∥∥解得BF=2.5.
【例3】∠ADE=∠C(答案不唯一)
3.1:D 解析:∵ 四边形ABCD 是平行四边形,∴AD=BC,AB=CD.A.若 即 又∵∠ECF = ∠BCD, ∴ △CEF ∽△CBD,∴∠CEF=∠CBD,∴EF∥BD,故A选项正确;B.若AE⊥BC,AF⊥CD,AE =AF,∴ CA 是∠BCD的角平分线,∴ ∠ACB =∠ACD.∵AD∥BC,∴ ∠DAC = ∠ACB,∴∠DAC =∠DCA,∴ AD = DC,∴ 四边形 ABCD 是菱形,∴ AC⊥BD.在Rt △ACE 和 Rt △AFC 中,,∴ Rt△ACE ≌Rt△AFC(HL),∴CE=CF.又∵AE =AF,∴AC⊥EF,∴EF∥BD,故 B 选项正确;C. ∵ CE = CF,∴ ∠CFE =∠CEF. ∵ EF ∥BD,∴ ∠CBD =∠CEF,∠CDB = ∠CFE,∴ ∠CBD=∠CDB,∴ CB = CD,∴ 四边形ABCD 是菱形,∴AC⊥BD. 又∵ EF∥BD,∴AC⊥EF.∵CE=CF,∴AC垂直平分 EF,∴AE=AF,∴∠EAC=∠FAC,故 C 选项正确;D.若AB=AD,则四边形 ABCD 是菱形.当AE=AF,且BE=DF时,可得AC垂直平分EF.∵AC⊥BD,∴EF∥BD,故D选项不正确.
3.2:证明:∵ BE=3,EC =6,CF=2,∴BC=3+6=9.
∵四边形ABCD 是正方形,∴AB=BC=9,∠B=∠C=90°.
【例4】C 4.1:14 4.2:12
4.3:证明:(1)∵ BD⊥AC,CE⊥AB,∴ ∠BDA=∠CEA=90°.
∵∠A =∠A,∴ △ABD∽△ACE.
(2)∵△ABD∽△ACE,∴ ∠OBE=∠OCD.
∵∠BOE=∠COD,∴△BOE∽△COD,∴
∵ ∠EOD =∠BOC,∴△OED∽△OBC,∴ ∠DEC=∠DBC.
4.4:解:(1)甲同学和乙同学的结论都正确.
证明:∵四边形ABCD 是矩形,∴ ∠D=∠BAD=90°.
由折叠,得∠D = ∠AEF = 90°=∠DAE,AD=AE,
∴ 四边形 AEFD 是正方形,故甲同学的结论正确.
如图,过点 G作GK⊥AF 于点 K.设AE=2x,则AG=EG=x.
∵四边形AEFD 是正方形,∴∠EAF=45°,
故乙同学的结论正确.
(2)如图,过点G作GQ⊥PM交PM的延长线于点 Q.
由折叠,得 FP =PM,FG=GM,GH
∴ 四边形 FGMP 是菱形,
【例5】
【例6】 20
6.1:B 6.2:D
达标训练
1. B 2. D 3. D 4. B 5. D
6. D 解析:∵ PB⊥PC,∴ 点 P 在以BC 为直径 的圆上. 如图所示.
∵四边形ABCD 是黄金矩形,
∴令∴⊙M的半径为
,∴AD边与⊙M 相离,
∴AD 边上满足 PB⊥PC 的点 P 的个数为0.
7.∠A=∠C(答案不唯一)
8. 9.2(答案不唯一)
10.证明:∵∠ACB=90°,∴∠A+∠B=90°.
∵DE⊥AB,∴ ∠ADE=∠ADC+∠CDE =90°.
∵CD=CA,∴∠A=∠ADC,∴∠CDE=∠B.
又∵∠DCE=∠BCD,∴ △CDE∽△CBD.
11. C 解析:因为图中12 个直角三角形都相似,所以 30°,即直角三角形中较小的锐角为30°.在 Rt△OAB中, cos ∠AOB 因为∠AOB =30°,所以 同理可得, 所以 又因为OA =1,所以
12. A
13.3 解析:∵ CD= CA,DE∥CB,∴CF是△ADE的中位线,∴AF=EF,DE =2CF =2.
∵ DE = DC,
∠CFA,∠ACF=∠ACB,∴ △CAF
∴2:BC=1:2,∴BC=4,∴BF=BC-FC=3.
解析:连接BE交AC于点O,如图.
∵五边形ABCDE是正五边形,
∴
∴△ABO
即 解得 或AC (不合题意,舍去),
经检验, 符合题意.
16.①②⑤
17.证明:∵ 四边形ABCD 是菱形,∴AB=BC,AC⊥BD.
又∵∠ABC=60°,∴ △ABC是等边三角形,∴AB=AC.
∵点F为BC的中点,∴AF⊥BC,∴ ∠BOC=∠BFE=90°.
又∵∠EBF=∠CBO,∴ △BEF∽△BCO.
18.解:(1)11.3.
(2)由反射定律可知,∠DCE=∠ACB.
又∵∠DEC=∠ABC=90°,∴△DEC∽△ABC,
即 解得AB=12,∴旗杆高度为12米.
(3)∵∠CDG =∠ADB,∠CGD =∠ABD=90°,.
设AB= xm,BD= ym,则
同理可得 解得
经检验, 是原方程的解,且符合题意.
∴雕塑高度AB 约为29 m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 三角形
第5节 相似三角形
考点分析
考点1 比例线段及其性质
课标要求导航:①了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割.②通过具体实例认识图形的相似.
例1(教材改编)下列四组线段中,不是成比例线段的是 ( )
1.1已知一个三角形的三边长分别为4,5,6,如果它与另一个三角形相似,那么另一个三角形的三边长可能是 ( )
A.2,3,4 B.8,10,12 C.12,15,20 D.15,20,30
1.2如图,点 P 把线段AB 分成两部分,且BP,AP,AB,BP是成比例线段.如果. 那么
考点2 平行线分线段成比例
课标要求导航:掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
例2 如图,在 中,D,E 分别为AB,AC上的点,连接DE,若 则 ( )
例2图 2.1图
2.1跨音乐学科 五线谱是一种记谱法,通过在五根等距离的平行横线上标以不同时值的音符及其他记号来记载音乐.如图,A,B,C为直线l与五线谱的横线相交的三个点,则 的值是 .
2.2如图, ∥∥求BC,BF的长.
考点3 相似三角形的判定与性质
课标要求导航:①了解相似三角形的判定定理:两角分别相等的两个三角形相似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似;②了解相似三角形判定定理的证明;③了解相似三角形的性质定理:相似三角形对应线段的比等于相似比;面积比等于相似比的平方.
例3 开放性设问 如图,在 中,点 D,E分别在边AB,AC 上.添加一个条件使△ADE∽△ACB,则这个条件可以是 .(写出一种情况即可)
例3图 3.1图
3.1如图,在 ABCD中,对角线AC,BD交于点O,点E在BC上,点F在CD上,连接AE,AF,EF,EF交AC 于点 G.下列结论错误的是 ( )
A.若 则EF∥BD B.若AE⊥BC,AF⊥CD,AE=AF,则EF∥BD
C.若EF∥BD,CE=CF,则∠EAC=∠FAC D.若AB=AD,AE=AF,则EF∥BD
3.2如图,点E,F分别在正方形ABCD的边BC,CD上,BE=3,EC=6,CF=2.求证:△ABE∽△ECF.
例4 如图, 为等边三角形,点D,E分别在边BC,AB上, 若 ,则AD 的长为( )
A.1.8 B.2.4 C.3 D.3.2
例4图 4.1图 4.2图
4.1如图,三角形纸片ABC 中, 分别沿与BC,AC平行的方向,从靠近A 的AB 边的三等分点剪去两个角,得到的平行四边形纸片的周长是 .
4.2如图, AD 与 BC 相交于点O,且. 与 的面积比是1:4,若 则CD 的长为 .
4.3中, 于点D, 于点E,BD,CE交于点O,连接DE.求证:
4.4综合与实践 某校数学课外活动小组用一张矩形纸片(如图1,矩形ABCD中, 且AB足够长)进行探究活动.
【动手操作】
如图2,第一步,沿点A 所在直线折叠,使点D 落在AB上的点E处,折痕为AF,连接EF,把纸片展平.
第二步,把四边形AEFD 折叠,使点A 与点 E 重合,点D 与点 F 重合,折痕为GH,再把纸片展平.
第三步,连接GF.
【探究发现】
根据以上操作,甲、乙两同学分别写出了一个结论.
甲同学的结论:四边形 AEFD 是正方形.
乙同学的结论:
(1)请分别判断甲、乙两同学的结论是否正确.若正确,写出证明过程;若不正确,请说明理由.
【继续探究】
在上面操作的基础上,丙同学继续操作.
如图3,第四步,沿点G 所在直线折叠,使点F落在AB上的点M处,折痕为GP,连接PM,把纸片展平.
第五步,连接 FM 交 GP 于点 N.
根据以上操作,丁同学写出了一个正确结论:
(2)请证明这个结论.
考点4 相似多边形
例5 已知矩形ABCD 中, ,在 BC上取一点 E,将 沿AE向上折叠,使点B 落在AD上的点 F 处.若四边形 EFDC 与矩形 ABCD相似,则
例5图 5.1图
5.1 如图,四边形ABCD和四边形EFGH 相似,且顶点都在方格纸的格点上,它们的相似比是 ( )
A.1:2 B.1:4 C.2:1 D.4:1
考点5 相似三角形的应用
课标要求导航:会利用图形的相似解决一些简单的实际问题.
例6 跨物理学科 物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图,燃烧的蜡烛(竖直放置)AB 经小孔 O 在屏幕(竖直放置)上成像. 设 小孔O到AB 的距离为30cm,则小孔O到 的距离为 cm.
【思路点拨】利用已知得出. ,进而利用相似三角形的性质求出即可.
6.1图1是伸缩折叠不锈钢晾衣架的实物图,图2是它的侧面示意图,AD 与 CB 相交于点 O, 根据图2中的数据可得x的值为 ( )
A.0.8 B.0.72 C.1.8 D.2
6.1图 6.2图
6.2数学文化 我国古代数学著作《九章算术》中的“井深”问题:“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何 ”,它的题意是:如图尺,尺,问井深BD是 ( )
A.1.25尺 B.56.5尺 C.6.25尺 D.57.5尺
达标训练
基础达标特训
1.已知一个三角形的三边长分别为4,5,6,如果它与另一个三角形相似,那么另一个三角形的三边长可能是 ( )
A.2,3,4 B.8,10,12 C.12,15,20 D.15,20,30
2.若两个相似三角形的相似比是1:3,则这两个相似三角形的面积比是( )
A.1:3 B.1:4 C.1:6 D.1:9
3.下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为 ( )
A.甲和乙 B.乙和丁 C.甲和丙 D.甲和丁
4.如图,在 ABCD 中,对角线AC,BD 相交于点 O,点 E 为 OC 的中点,EF∥AB交BC于点F.若AB=4,则 EF的长为 ( )
A. B.1 C. D.2
5.如图,矩形OABC 各顶点的坐标分别为O(0,0),A(3,0),B(3,2),C(0,2),以原点O 为位似中心,将这个矩形按相似比 缩小,则顶点B在第一象限对应点的坐标是 ( )
A.(9,4) B.(4,9) C.(1, ) D.(1, )
6.宽与长的比是 的矩形叫黄金矩形,黄金矩形给我们以协调的美感,世界各国许多著名建筑为取得最佳的视觉效果,都采用了黄金矩形的设计.已知四边形ABCD 是黄金矩形(AB
7.开放性设问 (2024 青海中考)如图,AC 和BD 相交于点O,请你添加一个条件 ,使得△AOB∽△COD.
8.)如图,AB 与 CD 交于点O,且AC∥BD.若 则
9.如图所示,四边形ABCD,DEFG,GHIJ 均为正方形,且 则正方形 DEFG的边长可以是 .(写出一个答案即可)
10.如图,在 Rt△ABC 中,∠ACB =90°,D 为边AB上一点,且 CD =CA,过点 D 作 DE⊥AB交BC 于点E.求证:△CDE∽△CBD.
高分提能特训
11.如图,是用12个相似的直角三角形组成的图案.若OA=1,则OG= ( )
C.
第11题图 第12题图
12.如图,在直角坐标系中,每个网格小正方形的边长均为1 个单位长度,以点 P 为位似中心作正方形PA A A ,正方形PA A A ,…,按此规律作下去,所作正方形的顶点均在格点上,其中正方形 PA A A 的顶点坐标分别为P( - 3,0),A (-2,1),A (-1,0),A (-2,-1),则顶点A 的坐标为 ( )
A.(31,34) B.(31,-34) C.(32,35) D.(32,0)
13.如图,在△ABC 中,延长AC至点D,使CD=CA,过点D 作DE∥CB,且 DE = DC,连接 AE 交 BC 于点 F. 若∠CAB=∠CFA,CF=1,则BF= .
第13题图 第14题图
14.如图,正五边形ABCDE 的边长为4,则这个正五边形的对角线AC 的长是 .
15.如图,△ABC中,A,B两个顶点在x轴的上方,点C 的坐标是(-1,0).以点 C 为位似中心,在x轴的下方作△ABC 的位似图形△A'B'C,并把△ABC 的边长放大到原来的2倍.设B'的坐标是(3,-1),则点 B 的坐标是 .
第15题图 第16题图
16.如图,△ABC中,AB=AC,∠BAC=90°,AD 是△ABC 的角平分线.
(1)以点 B 为圆心,适当长为半径画弧,分别交 BA,BC于点 E,F.
(2)以点A 为圆心,BE 长为半径画弧,交AC 于点 G.
(3)以点 G 为圆心,EF 长为半径画弧,与
(2)中所画的弧相交于点 H.
(4)画射线AH.
(5)以点B为圆心.,BC长为半径画弧,交射线AH于点 M.
(6)连接MC,MB. MB 分别交 AC,AD 于点N,P.
根据以上信息,下面五个结论中正确的是 .(只填序号)
①BD = CD;②∠ABM = 15°;③∠APN =∠ANP;④AMAD= ;⑤MC =MN·MB.
17.如图,在菱形 ABCD中,∠ABC =60°,对角线 AC 与 BD 相交于点O,点 F 为BC的中点,连接AF与BD相交于点E,连接CE 并延长交AB于点G.证明:△BEF∽△BCO.
冲刺满分特训
18.综合与实践 为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长 EF 恰好等于自己的身高 DE.此时,小组同学测得旗杆 AB 的影长 BC 为11.3m ,据此可得旗杆高度为 m;
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部
A.小组同学测得小李的眼睛距地面高度DE=1.5m ,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16 m.求旗杆高度;
(3)小王所在小组采用图3 的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P 处,用细线系小重物Q,标高线 PQ 始终垂直于水平地面.
如图6,在江姐故里广场上E 点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA 与标高线交点 C,测得标高 CG =1.8 m,DG =1.5m .将观测点 D 后移24 m到D'处.采用同样方法,测得C'G'=1. 2m,D'G'=2m.求雕塑高度(结果精确到1m).
参考答案
【例1】C 1.1:B 1.2:
【例2】B 2.1:2
2.2:解:∵∥∥
∵AB=3,AD=2,DE=4,解得BC=6.
∵∥∥解得BF=2.5.
【例3】∠ADE=∠C(答案不唯一)
3.1:D 解析:∵ 四边形ABCD 是平行四边形,∴AD=BC,AB=CD.A.若 即 又∵∠ECF = ∠BCD, ∴ △CEF ∽△CBD,∴∠CEF=∠CBD,∴EF∥BD,故A选项正确;B.若AE⊥BC,AF⊥CD,AE =AF,∴ CA 是∠BCD的角平分线,∴ ∠ACB =∠ACD.∵AD∥BC,∴ ∠DAC = ∠ACB,∴∠DAC =∠DCA,∴ AD = DC,∴ 四边形 ABCD 是菱形,∴ AC⊥BD.在Rt △ACE 和 Rt △AFC 中,,∴ Rt△ACE ≌Rt△AFC(HL),∴CE=CF.又∵AE =AF,∴AC⊥EF,∴EF∥BD,故 B 选项正确;C. ∵ CE = CF,∴ ∠CFE =∠CEF. ∵ EF ∥BD,∴ ∠CBD =∠CEF,∠CDB = ∠CFE,∴ ∠CBD=∠CDB,∴ CB = CD,∴ 四边形ABCD 是菱形,∴AC⊥BD. 又∵ EF∥BD,∴AC⊥EF.∵CE=CF,∴AC垂直平分 EF,∴AE=AF,∴∠EAC=∠FAC,故 C 选项正确;D.若AB=AD,则四边形 ABCD 是菱形.当AE=AF,且BE=DF时,可得AC垂直平分EF.∵AC⊥BD,∴EF∥BD,故D选项不正确.
3.2:证明:∵ BE=3,EC =6,CF=2,∴BC=3+6=9.
∵四边形ABCD 是正方形,∴AB=BC=9,∠B=∠C=90°.
【例4】C 4.1:14 4.2:12
4.3:证明:(1)∵ BD⊥AC,CE⊥AB,∴ ∠BDA=∠CEA=90°.
∵∠A =∠A,∴ △ABD∽△ACE.
(2)∵△ABD∽△ACE,∴ ∠OBE=∠OCD.
∵∠BOE=∠COD,∴△BOE∽△COD,∴
∵ ∠EOD =∠BOC,∴△OED∽△OBC,∴ ∠DEC=∠DBC.
4.4:解:(1)甲同学和乙同学的结论都正确.
证明:∵四边形ABCD 是矩形,∴ ∠D=∠BAD=90°.
由折叠,得∠D = ∠AEF = 90°=∠DAE,AD=AE,
∴ 四边形 AEFD 是正方形,故甲同学的结论正确.
如图,过点 G作GK⊥AF 于点 K.设AE=2x,则AG=EG=x.
∵四边形AEFD 是正方形,∴∠EAF=45°,
故乙同学的结论正确.
(2)如图,过点G作GQ⊥PM交PM的延长线于点 Q.
由折叠,得 FP =PM,FG=GM,GH
∴ 四边形 FGMP 是菱形,
【例5】
【例6】 20
6.1:B 6.2:D
达标训练
1. B 2. D 3. D 4. B 5. D
6. D 解析:∵ PB⊥PC,∴ 点 P 在以BC 为直径 的圆上. 如图所示.
∵四边形ABCD 是黄金矩形,
∴令∴⊙M的半径为
,∴AD边与⊙M 相离,
∴AD 边上满足 PB⊥PC 的点 P 的个数为0.
7.∠A=∠C(答案不唯一)
8. 9.2(答案不唯一)
10.证明:∵∠ACB=90°,∴∠A+∠B=90°.
∵DE⊥AB,∴ ∠ADE=∠ADC+∠CDE =90°.
∵CD=CA,∴∠A=∠ADC,∴∠CDE=∠B.
又∵∠DCE=∠BCD,∴ △CDE∽△CBD.
11. C 解析:因为图中12 个直角三角形都相似,所以 30°,即直角三角形中较小的锐角为30°.在 Rt△OAB中, cos ∠AOB 因为∠AOB =30°,所以 同理可得, 所以 又因为OA =1,所以
12. A
13.3 解析:∵ CD= CA,DE∥CB,∴CF是△ADE的中位线,∴AF=EF,DE =2CF =2.
∵ DE = DC,
∠CFA,∠ACF=∠ACB,∴ △CAF
∴2:BC=1:2,∴BC=4,∴BF=BC-FC=3.
解析:连接BE交AC于点O,如图.
∵五边形ABCDE是正五边形,
∴
∴△ABO
即 解得 或AC (不合题意,舍去),
经检验, 符合题意.
16.①②⑤
17.证明:∵ 四边形ABCD 是菱形,∴AB=BC,AC⊥BD.
又∵∠ABC=60°,∴ △ABC是等边三角形,∴AB=AC.
∵点F为BC的中点,∴AF⊥BC,∴ ∠BOC=∠BFE=90°.
又∵∠EBF=∠CBO,∴ △BEF∽△BCO.
18.解:(1)11.3.
(2)由反射定律可知,∠DCE=∠ACB.
又∵∠DEC=∠ABC=90°,∴△DEC∽△ABC,
即 解得AB=12,∴旗杆高度为12米.
(3)∵∠CDG =∠ADB,∠CGD =∠ABD=90°,.
设AB= xm,BD= ym,则
同理可得 解得
经检验, 是原方程的解,且符合题意.
∴雕塑高度AB 约为29 m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
