五四制鲁教版数学一轮复习 第四章 三角形 专项训练 解直角三角形实际应用模型(含答案)
文档属性
| 名称 | 五四制鲁教版数学一轮复习 第四章 三角形 专项训练 解直角三角形实际应用模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 381.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-16 17:18:39 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 三角形
专项训练 解直角三角形实际应用模型
模型一 “背靠背”型
【模型分析】
图形 模型特点
两直角三角形是并列关系,有公共直角顶点和一条公共直角边,其中,这条公共直角边是沟通两直角三角形的媒介
【针对训练】
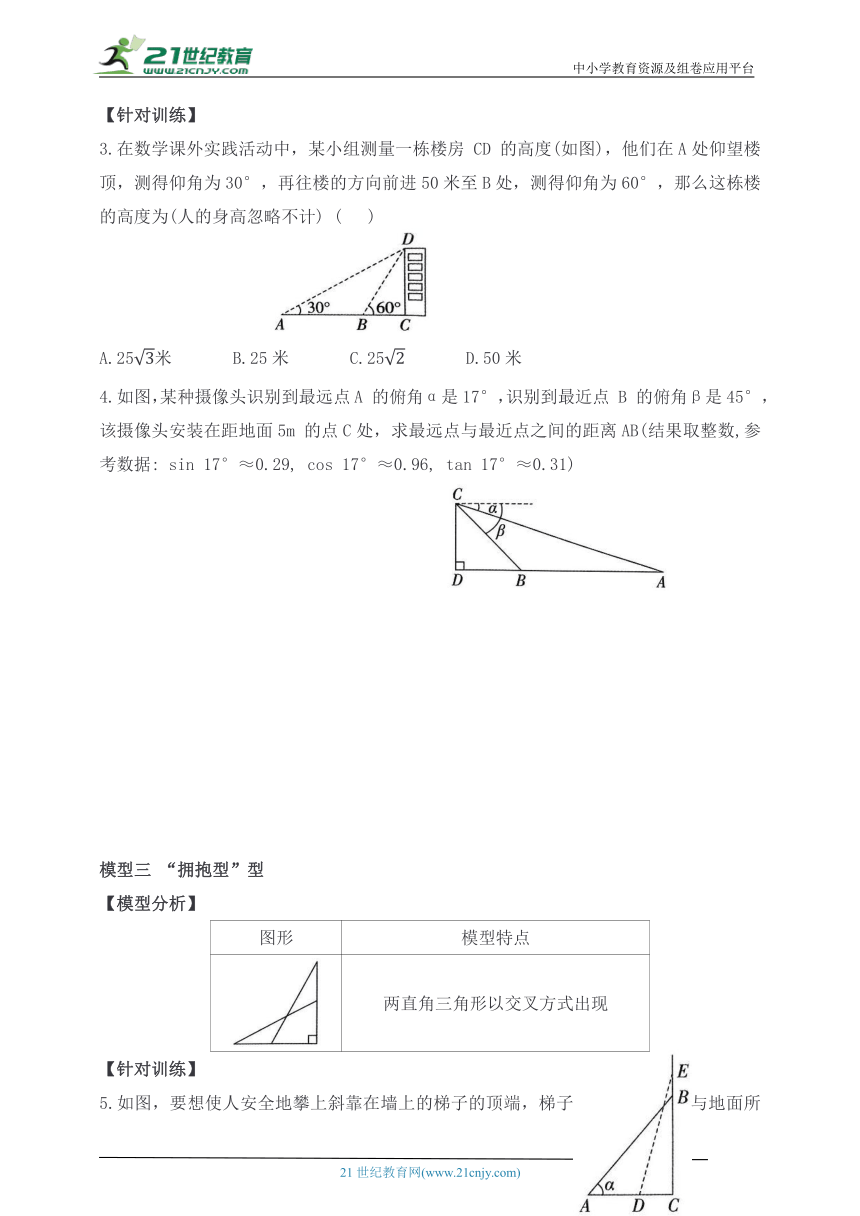
1.如图,用热气球的探测器测一栋楼的高度,从热气球上的点 A 测得该楼顶部点 C 的仰角为60°,测得底部点 B 的俯角为45°,点 A 与楼 BC 的水平距离 AD=50 m,则这 栋楼的 高 度 为 m(结果保留根号).
2.如图,一艘海轮位于灯塔P的北偏东37°方向,距离灯塔100 海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东45°方向上的B 处.这时,B处距离A处有多远 (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
模型二 “母抱子”型
【模型分析】
图形 模型特点
一个直角三角形包含在另一个直角三角形中,两直角三角形有公共直角和一条公共直角边,其中,这条公共直角边是沟通两直角三角形的媒介
【针对训练】
3.在数学课外实践活动中,某小组测量一栋楼房 CD 的高度(如图),他们在A处仰望楼顶,测得仰角为30°,再往楼的方向前进50米至B处,测得仰角为60°,那么这栋楼的高度为(人的身高忽略不计) ( )
A.25米 B.25米 C.25 D.50米
4.如图,某种摄像头识别到最远点A 的俯角α是17°,识别到最近点 B 的俯角β是45°,该摄像头安装在距地面5m 的点C处,求最远点与最近点之间的距离AB(结果取整数,参考数据: sin 17°≈0.29, cos 17°≈0.96, tan 17°≈0.31)
模型三 “拥抱型”型
【模型分析】
图形 模型特点
两直角三角形以交叉方式出现
【针对训练】
5.如图,要想使人安全地攀上斜靠在墙上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.现有一架斜靠在墙上的梯子,为了能够安全使用,该梯子前后移动的最大距离AD 为1.9m.使用这架梯子最高可以攀上多高的墙 (参考数据: sin 50°≈0.77, cos 50°≈0.64,t an50°≈1.19, sin 75°≈0.97,c os75°≈0.26,tan75°≈3.73)
6.某数学活动小组运用所学的解直角三角形知识测量楼房 FG 的楼顶安装的信号发射塔外墙 GH 的高度,利用测角仪和米尺等工具进行如下操作:在A 处测得∠GDF=30°,在B处测得∠HEF=50°,点A,B,C在一条直线上,AC⊥CH于点C,DF⊥CH于点F,AB 为20米,BC =40 米,测角仪的高度(AD,BE)为1.5米,请根据测量数据,求出信号发射塔 GH的值.(结果精确到1米,参考数据:
模型四 “斜截”型
【模型分析】
图形 模型特点
在一个直角三角形内,用垂直于斜边的一条直线去截这个直角三角形.新直角三角形与原直角三角形有一个公共锐角,所剩四边形的对角互补
【针对训练】
7.如图,已知一块四边形的草地ABCD,其中∠A=60°,∠B=∠D =90°,AB=20 m. CD=10 m.求这块草地的面积.
8.真实问题情境 芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索 AB 与水平桥面的夹角是30°,拉索 CD 与水平桥面的夹角是60°,两拉索底端距离 BD 为20 米,且已知两拉索顶端的距离AC为2米,请求出立柱AH 的长.(结果精确到0.1米,
参考答案
2.解:过P 作 PC⊥AB 于 C,如图.
在 Rt△APC中,∵∠A=37°,AP=100海里,∴ PC=AP· sin A =100×sin 37°≈100×0.60=60(海里),AC=AP·cos37°=100×0.80=80(海里).
在 Rt△PBC中,∵ ∠B=45°,∴BC=PC=60海里,∴AB=AC+BC=80+60=140(海里).
答:B处距离A处有140 海里.
3. A
4.解:如图,根据题意,得CE∥AD,CD=5 m.
∵CE∥AD,∴ ∠A = ∠α = 17°,∠CBD = ∠β=45°.
在Rt△ACD中,∴AD=5÷0.31=16.1(m).
在Rt△BCD中,∵∠CBD=45°,∴BD=CD=5m,
∴AB=AD-BD≈16.1 - 5 =11.1≈11(m).
答:最远点与最近点之间的距离AB约是11 m.
5.解:由题意,得AB=DE,BC⊥AC.
设AB=DE=x米,在Rt△ABC 中,∠BAC=50°,∴ AC=AB·cos50°≈0.64x米.
在Rt△EDC中,∠EDC=75°,∴ DC=ED·cos75°≈0.26x米.
∵AC-DC=AD,∴0.64x-0.26x=1.9,解得x=5,∴ DE=AB=5米,
在 Rt△EDC 中,EC = DE · sin 75°≈5×0.97=4.85(米),
∴使用这架梯子最高可以攀上高约为4.85 米的墙.
6.解:由题意知,DE =AB =20 米,EF=BC=40米,∴ DF=DE+EF=20+40=60(米).
在 Rt△DFG中,tan∠GDF = tan 30°
∴ FG=DF· tan 30°=60×20 34.6(米).
在 Rt△EFH 中,tan∠HEF = tan 50°
∴ FH =EF· tan 50°=40×1.19≈47.6(米),
∴ GH = FH - FG = 47. 6 - 34. 6 (米).
答:信号发射塔 GH 的长为13 米.
7.解:分别延长 AD,BC 交于点 E.如图所示.
E
∴四边形 ABCD 的面积
答:这块草地的面积为
8.解:设 米,
米,
米.
米.
解得
(米).
答:立柱AH的长约为16.3米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 三角形
专项训练 解直角三角形实际应用模型
模型一 “背靠背”型
【模型分析】
图形 模型特点
两直角三角形是并列关系,有公共直角顶点和一条公共直角边,其中,这条公共直角边是沟通两直角三角形的媒介
【针对训练】
1.如图,用热气球的探测器测一栋楼的高度,从热气球上的点 A 测得该楼顶部点 C 的仰角为60°,测得底部点 B 的俯角为45°,点 A 与楼 BC 的水平距离 AD=50 m,则这 栋楼的 高 度 为 m(结果保留根号).
2.如图,一艘海轮位于灯塔P的北偏东37°方向,距离灯塔100 海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东45°方向上的B 处.这时,B处距离A处有多远 (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
模型二 “母抱子”型
【模型分析】
图形 模型特点
一个直角三角形包含在另一个直角三角形中,两直角三角形有公共直角和一条公共直角边,其中,这条公共直角边是沟通两直角三角形的媒介
【针对训练】
3.在数学课外实践活动中,某小组测量一栋楼房 CD 的高度(如图),他们在A处仰望楼顶,测得仰角为30°,再往楼的方向前进50米至B处,测得仰角为60°,那么这栋楼的高度为(人的身高忽略不计) ( )
A.25米 B.25米 C.25 D.50米
4.如图,某种摄像头识别到最远点A 的俯角α是17°,识别到最近点 B 的俯角β是45°,该摄像头安装在距地面5m 的点C处,求最远点与最近点之间的距离AB(结果取整数,参考数据: sin 17°≈0.29, cos 17°≈0.96, tan 17°≈0.31)
模型三 “拥抱型”型
【模型分析】
图形 模型特点
两直角三角形以交叉方式出现
【针对训练】
5.如图,要想使人安全地攀上斜靠在墙上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.现有一架斜靠在墙上的梯子,为了能够安全使用,该梯子前后移动的最大距离AD 为1.9m.使用这架梯子最高可以攀上多高的墙 (参考数据: sin 50°≈0.77, cos 50°≈0.64,t an50°≈1.19, sin 75°≈0.97,c os75°≈0.26,tan75°≈3.73)
6.某数学活动小组运用所学的解直角三角形知识测量楼房 FG 的楼顶安装的信号发射塔外墙 GH 的高度,利用测角仪和米尺等工具进行如下操作:在A 处测得∠GDF=30°,在B处测得∠HEF=50°,点A,B,C在一条直线上,AC⊥CH于点C,DF⊥CH于点F,AB 为20米,BC =40 米,测角仪的高度(AD,BE)为1.5米,请根据测量数据,求出信号发射塔 GH的值.(结果精确到1米,参考数据:
模型四 “斜截”型
【模型分析】
图形 模型特点
在一个直角三角形内,用垂直于斜边的一条直线去截这个直角三角形.新直角三角形与原直角三角形有一个公共锐角,所剩四边形的对角互补
【针对训练】
7.如图,已知一块四边形的草地ABCD,其中∠A=60°,∠B=∠D =90°,AB=20 m. CD=10 m.求这块草地的面积.
8.真实问题情境 芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索 AB 与水平桥面的夹角是30°,拉索 CD 与水平桥面的夹角是60°,两拉索底端距离 BD 为20 米,且已知两拉索顶端的距离AC为2米,请求出立柱AH 的长.(结果精确到0.1米,
参考答案
2.解:过P 作 PC⊥AB 于 C,如图.
在 Rt△APC中,∵∠A=37°,AP=100海里,∴ PC=AP· sin A =100×sin 37°≈100×0.60=60(海里),AC=AP·cos37°=100×0.80=80(海里).
在 Rt△PBC中,∵ ∠B=45°,∴BC=PC=60海里,∴AB=AC+BC=80+60=140(海里).
答:B处距离A处有140 海里.
3. A
4.解:如图,根据题意,得CE∥AD,CD=5 m.
∵CE∥AD,∴ ∠A = ∠α = 17°,∠CBD = ∠β=45°.
在Rt△ACD中,∴AD=5÷0.31=16.1(m).
在Rt△BCD中,∵∠CBD=45°,∴BD=CD=5m,
∴AB=AD-BD≈16.1 - 5 =11.1≈11(m).
答:最远点与最近点之间的距离AB约是11 m.
5.解:由题意,得AB=DE,BC⊥AC.
设AB=DE=x米,在Rt△ABC 中,∠BAC=50°,∴ AC=AB·cos50°≈0.64x米.
在Rt△EDC中,∠EDC=75°,∴ DC=ED·cos75°≈0.26x米.
∵AC-DC=AD,∴0.64x-0.26x=1.9,解得x=5,∴ DE=AB=5米,
在 Rt△EDC 中,EC = DE · sin 75°≈5×0.97=4.85(米),
∴使用这架梯子最高可以攀上高约为4.85 米的墙.
6.解:由题意知,DE =AB =20 米,EF=BC=40米,∴ DF=DE+EF=20+40=60(米).
在 Rt△DFG中,tan∠GDF = tan 30°
∴ FG=DF· tan 30°=60×20 34.6(米).
在 Rt△EFH 中,tan∠HEF = tan 50°
∴ FH =EF· tan 50°=40×1.19≈47.6(米),
∴ GH = FH - FG = 47. 6 - 34. 6 (米).
答:信号发射塔 GH 的长为13 米.
7.解:分别延长 AD,BC 交于点 E.如图所示.
E
∴四边形 ABCD 的面积
答:这块草地的面积为
8.解:设 米,
米,
米.
米.
解得
(米).
答:立柱AH的长约为16.3米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
