五四制鲁教版数学一轮复习 第四章 三角形 专项训练 全等三角形归纳模型(含答案)
文档属性
| 名称 | 五四制鲁教版数学一轮复习 第四章 三角形 专项训练 全等三角形归纳模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 508.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-16 17:20:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
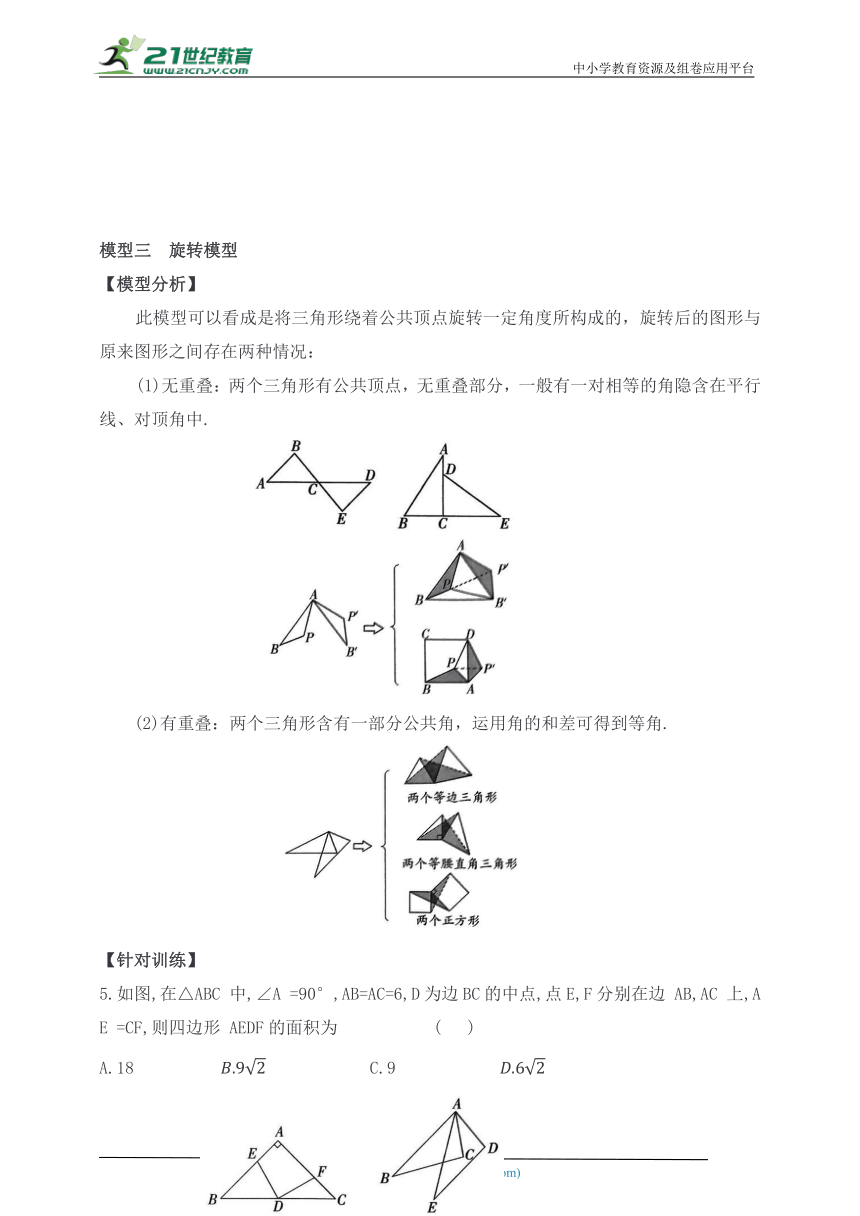
第四章 三角形
专项训练 全等三角形归纳模型
模型一 对称模型
【模型分析】
此模型的特征是所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边或公共角相等.
【针对训练】
1.如图,AB 是∠CAD 的平分线,AC=AD,求证:∠C=∠D.
2.如图,在△ABC 中,点 D 为BC边的中点,过点B作BE∥AC交AD 的延长线于点 E.
(1)求证:△BDE≌△CDA;
(2)若AD⊥BC,求证:BA=BE.
模型二 一线三等角模型
【模型分析】
一线:经过直角顶点的直线(BE);三垂直:直角边互相垂直(AC⊥CD),过直角的两边向直线作垂直(AB⊥BC,DE⊥CE),利用“同角的余角相等”转化找等角(∠1 =∠2).
【针对训练】
3.如图,AC∥DE,∠A=90°,B是 AD 上的一点,AC = BD,∠1 = ∠2. 判断△CBE的形状,并说明理由.
4.如图,在 中, 点D 在线段 BC 上运动(点 D不与点B、C 重合),连接AD,作 DE 交线段AC 于点 E.
(1)当 时,
(2)若 试说明
(3)在点 D 的运动过程中, 的形状可以是以AE 为腰的等腰三角形吗 若可以,求∠BDA 的度数;若不可以,请说明理由.
模型三 旋转模型
【模型分析】
此模型可以看成是将三角形绕着公共顶点旋转一定角度所构成的,旋转后的图形与原来图形之间存在两种情况:
(1)无重叠:两个三角形有公共顶点,无重叠部分,一般有一对相等的角隐含在平行线、对顶角中.
(2)有重叠:两个三角形含有一部分公共角,运用角的和差可得到等角.
【针对训练】
5.如图,在△ABC 中,∠A =90°,AB=AC=6,D为边BC的中点,点E,F分别在边 AB,AC 上,AE =CF,则四边形 AEDF的面积为 ( )
A.18 C.9
第5题图 第6题图
6.如图,在△ABC和△AED中,AB=AE,∠BAE=∠CAD,AC =AD.求证:△ABC≌△AED.
模型四 截长补短模型
【模型分析】
截长补短的方法适用于求证线段的和差倍分关系,截长,指在长线段中截取一段等于已知线段:补短,指将短线段延长,延长部分等于已知线段.该类题目中常出现等腰三角形、角平分线等.
【针对训练】
7.如图,在△ABC中,∠C=90°,∠B=45°,AD是△ABC的角平分线,求证:
模型五 半角模型
【模型分析】
过等腰三角形的顶点引两条射线,使两条射线的夹角为顶角的一半,半角模型常见于正方形、等边三角形、等腰直角三角形中,常用于证明线段之间的数量关系.
【针对训练】
8.如图,已知正方形ABCD,从顶点A 引两条射线分别交 BC,CD 于点 E,F,且 求证:
参考答案
1.证明:∵AB 是∠CAD 的平分线,∴ ∠CAB =∠DAB.
在△ABC 和△ABD中, ∴△ABC≌△ABD(SAS),∴∠C=∠D.
2.证明:(1)∵点D为BC的中点,∴BD=CD.
∵BE∥AC,∴∠EBD=∠C,∠E=∠CAD.
在△BDE 和△CDA中, ∴△BDE≌△CDA(AAS).
(2)∵点D为BC的中点,AD⊥BC,∴直线AD为线段BC的垂直平分线,∴BA=CA.
由(1)可知,△BDE≌△CDA,∴ BE=CA,∴ BA=BE.
3.解:△CBE 是等腰直角三角形.理由如下:
∵AC∥ED,∠A=90°,∴ ∠A=∠D=90°.
在△ABC和△EBD中, ∴△BCA≌△EBD(AAS),
∴BC=BE,∠ACB=∠EBD.
∵∠A=∠D=90°,∴∠1+∠ACB=90°.
∵∠ACB=∠EBD,∴∠1 +∠EBD=90°,∴∠CBE=90°,∴△CBE 是等腰直角三角形.
4.解:(1)20;62.
(2)∵AB=3,DC=3,∴AB=DC.
∵∠C=42°,∴∠DEC+∠EDC=138°.
∵∠ADE=42°,∴∠ADB+∠EDC=138°,∴∠ADB=∠DEC.
在△ABD和△DCE中, ∴△ABD≌△DCE(AAS).
(3)当∠BDA 的度数为 84°时,△ADE 的形状是以AE 为腰的等腰三角形.
①当AD =AE 时,∠AED = ∠ADE 此时,点D 与点 B 重合,不合题意;
②当 EA = ED 时,∠EAD = ∠ADE=42°,∵∠BDA+∠ADC=180°,∠CAD +∠C+∠ADC=180°.∴ ∠BDA = ∠EAD + ∠C =42°+
综上所述,当∠BDA 的度数为 84°时,△ADE的形状是以 AE 为腰的等腰三角形.
5. C
6.证明:∵∠BAE=∠CAD,∴ ∠BAE + ∠CAE = ∠CAD +∠CAE,即∠BAC=∠EAD.
在△ABC与△AED中, ∴△ABC≌△AED(SAS).
7.证明:如图,过点 D 作 DE⊥AB 于点 E.
∵AD 为△ABC 的角平分线,且 DE⊥AB,∠C=90°,∴CD=DE,∴∠AED=∠C=90°.
∵∠B=45°,∴∠BDE=∠B=45°,∴BE=DE,∴CD=DE=BE.
在Rt△ACD 和Rt△AED中,∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∴AB=AE+EB=AC+CD.
8.证明:如图,延长 CD 到 G,使 DG=BE.
∵在正方形ABCD中,AB=AD,∠B=∠ADC=90°,∴∠ADG=∠B.
在△ABE 和△ADG中,∴△ABE≌△ADG(SAS),
∴AG=AE,∠DAG=∠BAE.
∵ ∠EAF=45°,∴∠GAF =∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=90°-∴ ∠EAF=∠GAF.
在△AEF 和△AGF中,∴△AEF≌△AGF(SAS),∴ EF=GF.
∵GF=DG+DF=BE+DF,∴ BE+DF=EF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 三角形
专项训练 全等三角形归纳模型
模型一 对称模型
【模型分析】
此模型的特征是所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边或公共角相等.
【针对训练】
1.如图,AB 是∠CAD 的平分线,AC=AD,求证:∠C=∠D.
2.如图,在△ABC 中,点 D 为BC边的中点,过点B作BE∥AC交AD 的延长线于点 E.
(1)求证:△BDE≌△CDA;
(2)若AD⊥BC,求证:BA=BE.
模型二 一线三等角模型
【模型分析】
一线:经过直角顶点的直线(BE);三垂直:直角边互相垂直(AC⊥CD),过直角的两边向直线作垂直(AB⊥BC,DE⊥CE),利用“同角的余角相等”转化找等角(∠1 =∠2).
【针对训练】
3.如图,AC∥DE,∠A=90°,B是 AD 上的一点,AC = BD,∠1 = ∠2. 判断△CBE的形状,并说明理由.
4.如图,在 中, 点D 在线段 BC 上运动(点 D不与点B、C 重合),连接AD,作 DE 交线段AC 于点 E.
(1)当 时,
(2)若 试说明
(3)在点 D 的运动过程中, 的形状可以是以AE 为腰的等腰三角形吗 若可以,求∠BDA 的度数;若不可以,请说明理由.
模型三 旋转模型
【模型分析】
此模型可以看成是将三角形绕着公共顶点旋转一定角度所构成的,旋转后的图形与原来图形之间存在两种情况:
(1)无重叠:两个三角形有公共顶点,无重叠部分,一般有一对相等的角隐含在平行线、对顶角中.
(2)有重叠:两个三角形含有一部分公共角,运用角的和差可得到等角.
【针对训练】
5.如图,在△ABC 中,∠A =90°,AB=AC=6,D为边BC的中点,点E,F分别在边 AB,AC 上,AE =CF,则四边形 AEDF的面积为 ( )
A.18 C.9
第5题图 第6题图
6.如图,在△ABC和△AED中,AB=AE,∠BAE=∠CAD,AC =AD.求证:△ABC≌△AED.
模型四 截长补短模型
【模型分析】
截长补短的方法适用于求证线段的和差倍分关系,截长,指在长线段中截取一段等于已知线段:补短,指将短线段延长,延长部分等于已知线段.该类题目中常出现等腰三角形、角平分线等.
【针对训练】
7.如图,在△ABC中,∠C=90°,∠B=45°,AD是△ABC的角平分线,求证:
模型五 半角模型
【模型分析】
过等腰三角形的顶点引两条射线,使两条射线的夹角为顶角的一半,半角模型常见于正方形、等边三角形、等腰直角三角形中,常用于证明线段之间的数量关系.
【针对训练】
8.如图,已知正方形ABCD,从顶点A 引两条射线分别交 BC,CD 于点 E,F,且 求证:
参考答案
1.证明:∵AB 是∠CAD 的平分线,∴ ∠CAB =∠DAB.
在△ABC 和△ABD中, ∴△ABC≌△ABD(SAS),∴∠C=∠D.
2.证明:(1)∵点D为BC的中点,∴BD=CD.
∵BE∥AC,∴∠EBD=∠C,∠E=∠CAD.
在△BDE 和△CDA中, ∴△BDE≌△CDA(AAS).
(2)∵点D为BC的中点,AD⊥BC,∴直线AD为线段BC的垂直平分线,∴BA=CA.
由(1)可知,△BDE≌△CDA,∴ BE=CA,∴ BA=BE.
3.解:△CBE 是等腰直角三角形.理由如下:
∵AC∥ED,∠A=90°,∴ ∠A=∠D=90°.
在△ABC和△EBD中, ∴△BCA≌△EBD(AAS),
∴BC=BE,∠ACB=∠EBD.
∵∠A=∠D=90°,∴∠1+∠ACB=90°.
∵∠ACB=∠EBD,∴∠1 +∠EBD=90°,∴∠CBE=90°,∴△CBE 是等腰直角三角形.
4.解:(1)20;62.
(2)∵AB=3,DC=3,∴AB=DC.
∵∠C=42°,∴∠DEC+∠EDC=138°.
∵∠ADE=42°,∴∠ADB+∠EDC=138°,∴∠ADB=∠DEC.
在△ABD和△DCE中, ∴△ABD≌△DCE(AAS).
(3)当∠BDA 的度数为 84°时,△ADE 的形状是以AE 为腰的等腰三角形.
①当AD =AE 时,∠AED = ∠ADE 此时,点D 与点 B 重合,不合题意;
②当 EA = ED 时,∠EAD = ∠ADE=42°,∵∠BDA+∠ADC=180°,∠CAD +∠C+∠ADC=180°.∴ ∠BDA = ∠EAD + ∠C =42°+
综上所述,当∠BDA 的度数为 84°时,△ADE的形状是以 AE 为腰的等腰三角形.
5. C
6.证明:∵∠BAE=∠CAD,∴ ∠BAE + ∠CAE = ∠CAD +∠CAE,即∠BAC=∠EAD.
在△ABC与△AED中, ∴△ABC≌△AED(SAS).
7.证明:如图,过点 D 作 DE⊥AB 于点 E.
∵AD 为△ABC 的角平分线,且 DE⊥AB,∠C=90°,∴CD=DE,∴∠AED=∠C=90°.
∵∠B=45°,∴∠BDE=∠B=45°,∴BE=DE,∴CD=DE=BE.
在Rt△ACD 和Rt△AED中,∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∴AB=AE+EB=AC+CD.
8.证明:如图,延长 CD 到 G,使 DG=BE.
∵在正方形ABCD中,AB=AD,∠B=∠ADC=90°,∴∠ADG=∠B.
在△ABE 和△ADG中,∴△ABE≌△ADG(SAS),
∴AG=AE,∠DAG=∠BAE.
∵ ∠EAF=45°,∴∠GAF =∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=90°-∴ ∠EAF=∠GAF.
在△AEF 和△AGF中,∴△AEF≌△AGF(SAS),∴ EF=GF.
∵GF=DG+DF=BE+DF,∴ BE+DF=EF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
