18.2 特殊的平行四边形 课时培优(含答案) 2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 18.2 特殊的平行四边形 课时培优(含答案) 2024-2025学年人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 390.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-16 00:00:00 | ||
图片预览



文档简介
18.2特殊的平行四边形 课时培优 2024-2025学年人教版数学八年级下
一、单选题
1.如图,四边形为平行四边形,延长到,使,连接,下列条件中,不能使四边形成为菱形的是( )
A. B. C. D.平分
2.如图,E、F分别是正方形的边、上的点,且,和相交于点O,有下列结论:
①;②;③;④.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
3.如图,已知菱形ABCD的对角线AC.BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是()
A. B. C. D.
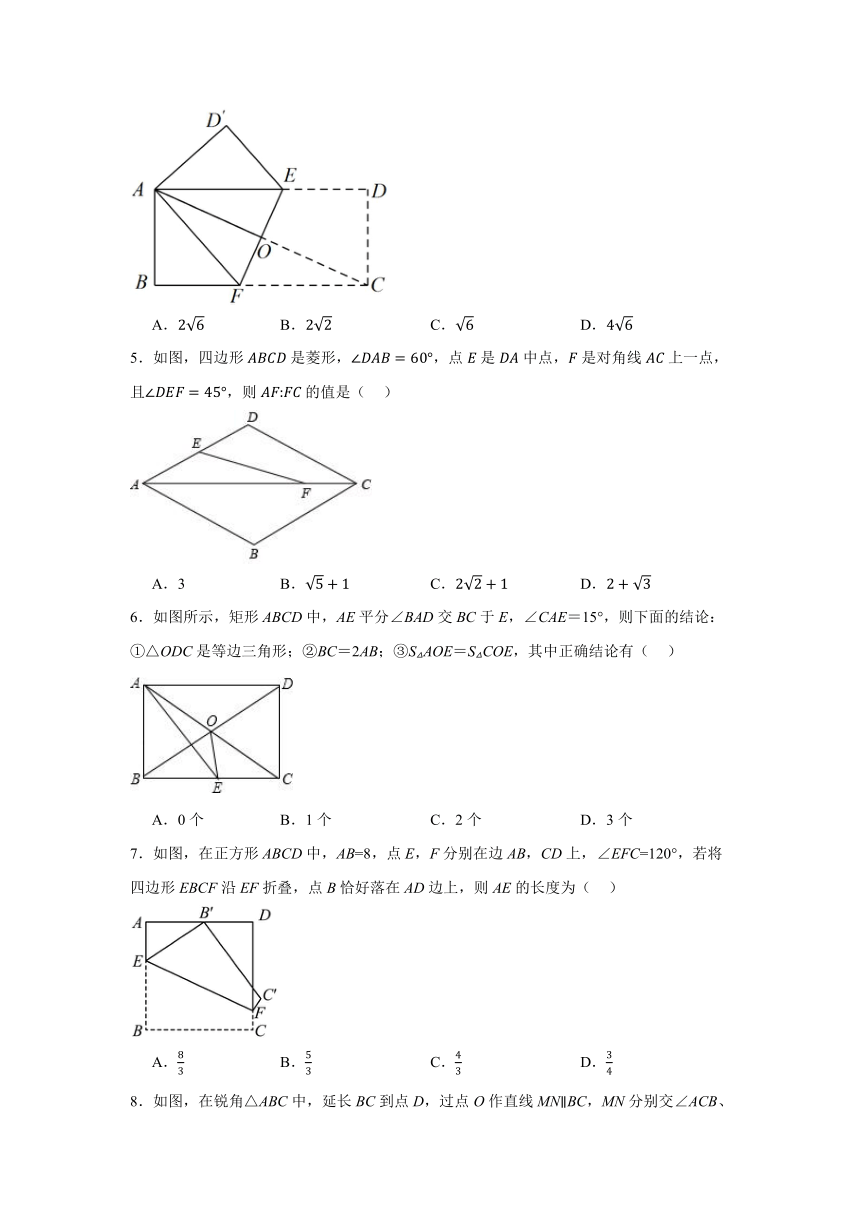
4.如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O.若AE=3,BF=1,则AC的长为( )
A. B. C. D.
5.如图,四边形是菱形,,点是中点,是对角线上一点,且,则的值是( )
A.3 B. C. D.
6.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:①△ODC是等边三角形;②BC=2AB;③S△AOE=S△COE,其中正确结论有( )
A.0个 B.1个 C.2个 D.3个
7.如图,在正方形ABCD中,AB=8,点E,F分别在边AB,CD上,∠EFC=120°,若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则AE的长度为( )
A. B. C. D.
8.如图,在锐角△ABC中,延长BC到点D,过点O作直线MNBC,MN分别交∠ACB、∠ACD的平分线于E,连接AE、AF,在下列结论中:①OE=OF;②CE=CF;③若CE=12,则OC的长为6;④当AO=CO时,四边形AECF是矩形.其中正确的是( )
A.①④ B.①② C.①②③ D.②③④
二、填空题
9.如图,在直角三角形ABC中,斜边上的中线CD=AC,则∠B= °.
10.如图,矩形ABCD的对角线AC和BD相交于点O,直线EF经过点O,交BC于点E,AD于点F,若AB=5cm,AC=13 cm,则阴影部分的面积为 .
11.如图,连接四边形ABCD各边的中点,得到四边形EFGH,还要添加 ,才能保证四边形EFGH是正方形.
12.如图,菱形ABCD的周长为48cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于 .
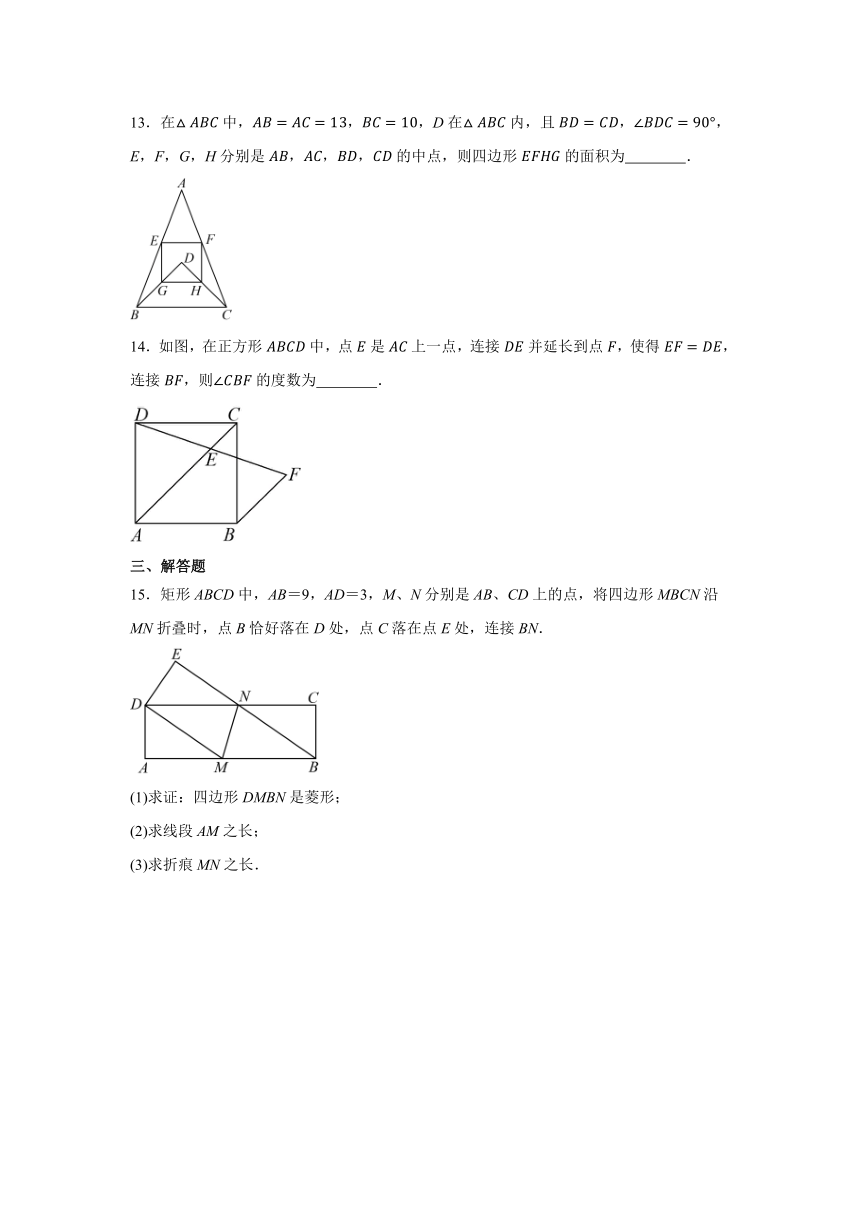
13.在中,,D在内,且,E,F,G,H分别是的中点,则四边形的面积为 .
14.如图,在正方形中,点是上一点,连接并延长到点,使得,连接,则的度数为 .
三、解答题
15.矩形ABCD中,AB=9,AD=3,M、N分别是AB、CD上的点,将四边形MBCN沿MN折叠时,点B恰好落在D处,点C落在点E处,连接BN.
(1)求证:四边形DMBN是菱形;
(2)求线段AM之长;
(3)求折痕MN之长.
16.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且EAC是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若AC=8,AB=5,求ED的长.
17.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
18.已知,在正方形ABCD中,连接对角线BD,点E为射线CB上一点,连接AE.F是AE的中点,过点F作FM⊥AE于F,FM交直线BD于M,连接ME、MC.
(1)如图1,当点E在CB边上时.
①依题意补全图1;
②猜想∠MEC与∠MCE之间的数量关系,并证明.
(2)如图2,当点E在CB边的延长线上时,补全图2,并直接写出AE与MC之间的数量关系.
参考答案
1.A
2.B
3.D
4.A
5.D
6.C
7.A
8.A
9.30°.
10.15cm2
11.AC⊥BD,AC=BD
12.
13.
14.
15.(1)证明:根据题意得:BM=DM,DN=BN,∠DMN=∠BMN,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DNM=∠BMN,
∴∠DNM=∠DMN,
∴DM=DN,
∴DM=BM=DN=BN,
∴四边形DMBN是菱形;
(2)解:设AM=x,则DM=BM=AB-AM=9-x,
∵四边形ABCD是矩形,
∴∠A=90°,
在中,,
∴,解得:x=4,
即AM=4;
(3)解:如图,连接BD,
∵四边形ABCD是矩形,
∴∠A=90°,
在中, AB=9,AD=3,
∴,
由(2)得:AM=4,
∴BM=5,
∵,
∴,
解得:.
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,
∵△EAC是等边三角形,
∴EA=EC,
∴EO⊥AC,
∴四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,AC=8,
∴AO=CO=4,DO=BO,
在Rt△ABO中,BO= =3,
∴DO=BO=3,
在Rt△EAO中,EO==,
∴ED=EO-DO=-3.
17.解:(1)证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,4=∠6.
∵MN∥BC,
∴∠1=∠5,3=∠6.
∴∠1=∠2,∠3=∠4.
∴EO=CO,FO=CO.
∴OE=OF.
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°.
∵CE=12,CF=5,
∴.
∴OC=EF=6.5.
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:
当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形.
∵∠ECF=90°,
∴平行四边形AECF是矩形.
18.(1)解:①补全图如图所示,
②∠MEC=∠MCE,
证明:连接AM,
∵F是AE的中点,FM⊥AE,
∴MA=ME,
∵四边形ABCD是正方形,BD是对角线,
∴∠ADM=∠CDM,AD=CD,
在△ADM和△CDM中,,
∴△ADM≌△CDM(ASA),
∴MA=MC,
∴ME=MC,
∴∠MEC=∠MCE;
(2)解:AE=CM,
证明:补全图如图所示,连接MA,
,
∵F是AE的中点,FM⊥AE,
∴MA=ME,
∵四边形ABCD是正方形,BD是对角线,
∴∠ADM=∠CDM,AD=CD,
在△ADM和△CDM中,,
∴△ADM≌△CDM(ASA),
∴MA=MC,∠MAD=∠MCD,
∵∠MEC=∠MCE,
∴∠MEC+∠MAD=∠DCM+∠MCE=90°,
∵AD∥CE,
∴∠DAE+∠CEA=180°,
∴∠MAE+∠MEA=90°,
∴∠AME=90°,
∴△EMA是等腰直角三角形,
∴AE=AM=CM.
一、单选题
1.如图,四边形为平行四边形,延长到,使,连接,下列条件中,不能使四边形成为菱形的是( )
A. B. C. D.平分
2.如图,E、F分别是正方形的边、上的点,且,和相交于点O,有下列结论:
①;②;③;④.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
3.如图,已知菱形ABCD的对角线AC.BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是()
A. B. C. D.
4.如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O.若AE=3,BF=1,则AC的长为( )
A. B. C. D.
5.如图,四边形是菱形,,点是中点,是对角线上一点,且,则的值是( )
A.3 B. C. D.
6.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:①△ODC是等边三角形;②BC=2AB;③S△AOE=S△COE,其中正确结论有( )
A.0个 B.1个 C.2个 D.3个
7.如图,在正方形ABCD中,AB=8,点E,F分别在边AB,CD上,∠EFC=120°,若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则AE的长度为( )
A. B. C. D.
8.如图,在锐角△ABC中,延长BC到点D,过点O作直线MNBC,MN分别交∠ACB、∠ACD的平分线于E,连接AE、AF,在下列结论中:①OE=OF;②CE=CF;③若CE=12,则OC的长为6;④当AO=CO时,四边形AECF是矩形.其中正确的是( )
A.①④ B.①② C.①②③ D.②③④
二、填空题
9.如图,在直角三角形ABC中,斜边上的中线CD=AC,则∠B= °.
10.如图,矩形ABCD的对角线AC和BD相交于点O,直线EF经过点O,交BC于点E,AD于点F,若AB=5cm,AC=13 cm,则阴影部分的面积为 .
11.如图,连接四边形ABCD各边的中点,得到四边形EFGH,还要添加 ,才能保证四边形EFGH是正方形.
12.如图,菱形ABCD的周长为48cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于 .
13.在中,,D在内,且,E,F,G,H分别是的中点,则四边形的面积为 .
14.如图,在正方形中,点是上一点,连接并延长到点,使得,连接,则的度数为 .
三、解答题
15.矩形ABCD中,AB=9,AD=3,M、N分别是AB、CD上的点,将四边形MBCN沿MN折叠时,点B恰好落在D处,点C落在点E处,连接BN.
(1)求证:四边形DMBN是菱形;
(2)求线段AM之长;
(3)求折痕MN之长.
16.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且EAC是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若AC=8,AB=5,求ED的长.
17.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
18.已知,在正方形ABCD中,连接对角线BD,点E为射线CB上一点,连接AE.F是AE的中点,过点F作FM⊥AE于F,FM交直线BD于M,连接ME、MC.
(1)如图1,当点E在CB边上时.
①依题意补全图1;
②猜想∠MEC与∠MCE之间的数量关系,并证明.
(2)如图2,当点E在CB边的延长线上时,补全图2,并直接写出AE与MC之间的数量关系.
参考答案
1.A
2.B
3.D
4.A
5.D
6.C
7.A
8.A
9.30°.
10.15cm2
11.AC⊥BD,AC=BD
12.
13.
14.
15.(1)证明:根据题意得:BM=DM,DN=BN,∠DMN=∠BMN,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DNM=∠BMN,
∴∠DNM=∠DMN,
∴DM=DN,
∴DM=BM=DN=BN,
∴四边形DMBN是菱形;
(2)解:设AM=x,则DM=BM=AB-AM=9-x,
∵四边形ABCD是矩形,
∴∠A=90°,
在中,,
∴,解得:x=4,
即AM=4;
(3)解:如图,连接BD,
∵四边形ABCD是矩形,
∴∠A=90°,
在中, AB=9,AD=3,
∴,
由(2)得:AM=4,
∴BM=5,
∵,
∴,
解得:.
16.解:(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,
∵△EAC是等边三角形,
∴EA=EC,
∴EO⊥AC,
∴四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,AC=8,
∴AO=CO=4,DO=BO,
在Rt△ABO中,BO= =3,
∴DO=BO=3,
在Rt△EAO中,EO==,
∴ED=EO-DO=-3.
17.解:(1)证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,4=∠6.
∵MN∥BC,
∴∠1=∠5,3=∠6.
∴∠1=∠2,∠3=∠4.
∴EO=CO,FO=CO.
∴OE=OF.
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°.
∵CE=12,CF=5,
∴.
∴OC=EF=6.5.
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:
当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形.
∵∠ECF=90°,
∴平行四边形AECF是矩形.
18.(1)解:①补全图如图所示,
②∠MEC=∠MCE,
证明:连接AM,
∵F是AE的中点,FM⊥AE,
∴MA=ME,
∵四边形ABCD是正方形,BD是对角线,
∴∠ADM=∠CDM,AD=CD,
在△ADM和△CDM中,,
∴△ADM≌△CDM(ASA),
∴MA=MC,
∴ME=MC,
∴∠MEC=∠MCE;
(2)解:AE=CM,
证明:补全图如图所示,连接MA,
,
∵F是AE的中点,FM⊥AE,
∴MA=ME,
∵四边形ABCD是正方形,BD是对角线,
∴∠ADM=∠CDM,AD=CD,
在△ADM和△CDM中,,
∴△ADM≌△CDM(ASA),
∴MA=MC,∠MAD=∠MCD,
∵∠MEC=∠MCE,
∴∠MEC+∠MAD=∠DCM+∠MCE=90°,
∵AD∥CE,
∴∠DAE+∠CEA=180°,
∴∠MAE+∠MEA=90°,
∴∠AME=90°,
∴△EMA是等腰直角三角形,
∴AE=AM=CM.
