17.1 第2课时 勾股定理的实际应用 课件(共17张PPT)
文档属性
| 名称 | 17.1 第2课时 勾股定理的实际应用 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 607.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-16 19:48:03 | ||
图片预览





文档简介
(共17张PPT)
人教版八年级数学下册
第17章 勾股定理
17.1 勾股定理
第2课时 勾股定理的实际应用
学习目标
1. 能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长之间的联系,并进一步求出未知边的长度.
2. 会运用勾股定理解决简单的实际问题.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
A
B
C
几何语言:在Rt△ ABC中,∠C=90°,
∴
结论变形:
回顾旧知
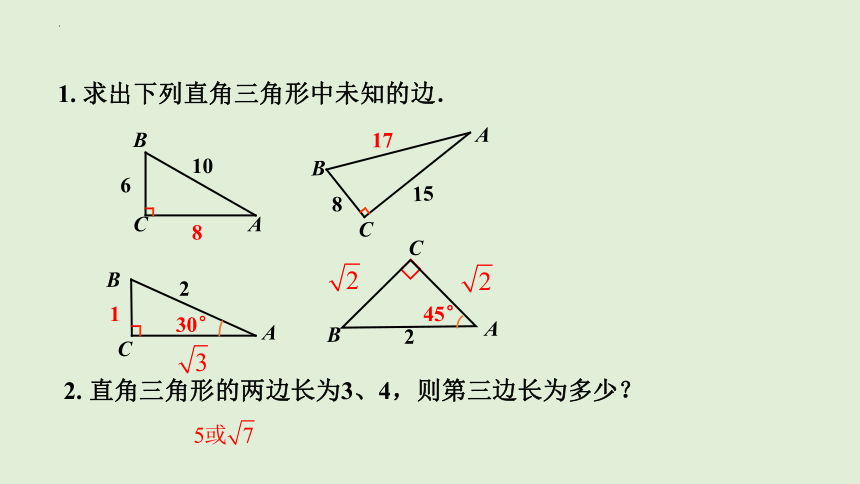
1. 求出下列直角三角形中未知的边.
6
10
A
C
B
8
A
15
C
B
30°
2
2
45°
A
C
B
A
C
B
8
17
1
2. 直角三角形的两边长为3、4,则第三边长为多少?
例1:一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么
2m
1m
A
B
D
C
解:连接AC
AC2=AB2+BC2=12+22=5
因为AC大于木板的宽2.2m,所以木板能从门框内通过.
在Rt△ABC中,∠B=90°
典例分析
A
B
D
C
O
解:在Rt△AOB中,∠AOB=90°
OB2=AB2-OA2=2.62-2.42=1,
∴OB=1.
在Rt△COD中,∠COD=90°
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
∴梯子的顶端沿墙下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
例2:如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
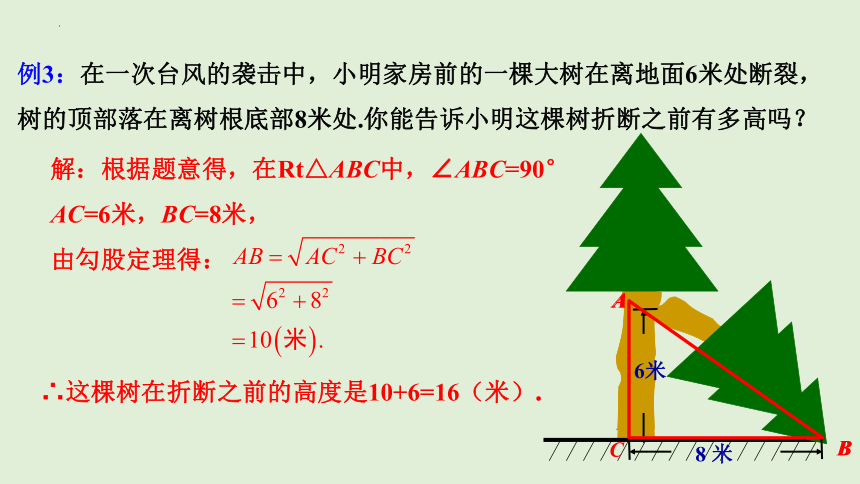
8 米
6米
A
C
B
解:根据题意得,在Rt△ABC中,∠ABC=90°
AC=6米,BC=8米,
由勾股定理得:
∴这棵树在折断之前的高度是10+6=16(米).
例3:在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗?
A
B
利用勾股定理解决实际问题的基本思路:
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
总结归纳
1. 湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A. 50米 B. 120米 C. 100米 D. 130米
2. 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
A. 9cm B. 12cm C. 15cm D. 18cm
当堂巩固
A
D
C
A
B
3. 如图,学校教学楼前有一块长方形长为4米,宽为3米的草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“径路”,却踩伤了花草.
(1)求这条“径路”的长;
(2)他们仅仅少走了几步(假设2步为1米)?
解:(1)在Rt△ ABC中,
根据勾股定理得
∴这条“径路”的长为5米.
(2)他们仅仅少走了 (3+4-5)×2=4(步).
别踩我,我怕疼!
如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
C
A
E
B
D
x
25-x
15
10
能力提升
解:设AE= x km,
在Rt△ ADE和Rt△ EBC中,
AD2+AE2=DE2
BC2+BE2=CE2
又 ∵ DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
答:E站应建在离A站10km处.
∴ x=10
则 BE=(25-x)km
C
A
E
B
D
x
25-x
15
10
1. 某工程队准备从A到B修建一条隧道,测量员在直线AB的同一侧选定C,D两个观测点,如图.测得AC长为 km,CD长为 km,BD长为 km,∠ACD=60°,∠CDB=135°(A、B、C、D在同一水平面内).
(1)求A、D两点之间的距离;
(2)求隧道AB的长度.
感受中考
【解答】解:(1)过A作AE⊥CD于E,如图所示:
则∠AEC=∠AED=90°,
∵∠ACD=60°,
∴∠CAE=90°-60°=30°,
∴ , ,
∴ ,
∴AE=DE,
∴△ADE是等腰直角三角形,
∴ .
(2)由(1)得:△ADE是等腰直角三角形,
∴ ,∠ADE=45°,
∵∠CDB=135°,
∴∠ADB=135°-45°=90°,
∴ ,
即隧道AB的长度为3 km.
本节课主要学习了如何运用勾股定理解决实际问题.
基本思路:
课堂小结
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
P28:习题17.1:第2、4、5题.
P29:习题17.1:第10题.
布置作业
人教版八年级数学下册
第17章 勾股定理
17.1 勾股定理
第2课时 勾股定理的实际应用
学习目标
1. 能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长之间的联系,并进一步求出未知边的长度.
2. 会运用勾股定理解决简单的实际问题.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
A
B
C
几何语言:在Rt△ ABC中,∠C=90°,
∴
结论变形:
回顾旧知
1. 求出下列直角三角形中未知的边.
6
10
A
C
B
8
A
15
C
B
30°
2
2
45°
A
C
B
A
C
B
8
17
1
2. 直角三角形的两边长为3、4,则第三边长为多少?
例1:一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么
2m
1m
A
B
D
C
解:连接AC
AC2=AB2+BC2=12+22=5
因为AC大于木板的宽2.2m,所以木板能从门框内通过.
在Rt△ABC中,∠B=90°
典例分析
A
B
D
C
O
解:在Rt△AOB中,∠AOB=90°
OB2=AB2-OA2=2.62-2.42=1,
∴OB=1.
在Rt△COD中,∠COD=90°
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
∴梯子的顶端沿墙下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
例2:如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
8 米
6米
A
C
B
解:根据题意得,在Rt△ABC中,∠ABC=90°
AC=6米,BC=8米,
由勾股定理得:
∴这棵树在折断之前的高度是10+6=16(米).
例3:在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗?
A
B
利用勾股定理解决实际问题的基本思路:
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
总结归纳
1. 湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A. 50米 B. 120米 C. 100米 D. 130米
2. 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
A. 9cm B. 12cm C. 15cm D. 18cm
当堂巩固
A
D
C
A
B
3. 如图,学校教学楼前有一块长方形长为4米,宽为3米的草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“径路”,却踩伤了花草.
(1)求这条“径路”的长;
(2)他们仅仅少走了几步(假设2步为1米)?
解:(1)在Rt△ ABC中,
根据勾股定理得
∴这条“径路”的长为5米.
(2)他们仅仅少走了 (3+4-5)×2=4(步).
别踩我,我怕疼!
如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
C
A
E
B
D
x
25-x
15
10
能力提升
解:设AE= x km,
在Rt△ ADE和Rt△ EBC中,
AD2+AE2=DE2
BC2+BE2=CE2
又 ∵ DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
答:E站应建在离A站10km处.
∴ x=10
则 BE=(25-x)km
C
A
E
B
D
x
25-x
15
10
1. 某工程队准备从A到B修建一条隧道,测量员在直线AB的同一侧选定C,D两个观测点,如图.测得AC长为 km,CD长为 km,BD长为 km,∠ACD=60°,∠CDB=135°(A、B、C、D在同一水平面内).
(1)求A、D两点之间的距离;
(2)求隧道AB的长度.
感受中考
【解答】解:(1)过A作AE⊥CD于E,如图所示:
则∠AEC=∠AED=90°,
∵∠ACD=60°,
∴∠CAE=90°-60°=30°,
∴ , ,
∴ ,
∴AE=DE,
∴△ADE是等腰直角三角形,
∴ .
(2)由(1)得:△ADE是等腰直角三角形,
∴ ,∠ADE=45°,
∵∠CDB=135°,
∴∠ADB=135°-45°=90°,
∴ ,
即隧道AB的长度为3 km.
本节课主要学习了如何运用勾股定理解决实际问题.
基本思路:
课堂小结
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
P28:习题17.1:第2、4、5题.
P29:习题17.1:第10题.
布置作业
