18.2.3 第2课时 正方形的判定 课件(共20张PPT)人教版数学八年级下册
文档属性
| 名称 | 18.2.3 第2课时 正方形的判定 课件(共20张PPT)人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 564.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-16 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
18.2.3 正方形
(第2课时)
2.正方形的性质:
1.正方形的定义:
有一组邻边相等,且有一个角是直角的平行四边形是正方形.
(1)边:四条边相等.
(2)角:四个角都是直角.
(3)对角线:对角线相等,且互相垂直平分.
(4)对称性:正方形是轴对称图形,有四条对称轴,分别是对边中点所在的直线以及两条对角线所在的直线.
由正方形的定义可知,有一组邻边相等,且有一个角是直角的平行四边形是正方形.除此之外,还有没有其他判定方法呢?
上节课,我们学过:
(1)有一组邻边相等的矩形是正方形.
(2)有一个角是直角的菱形是正方形.
你能分别给出证明吗?
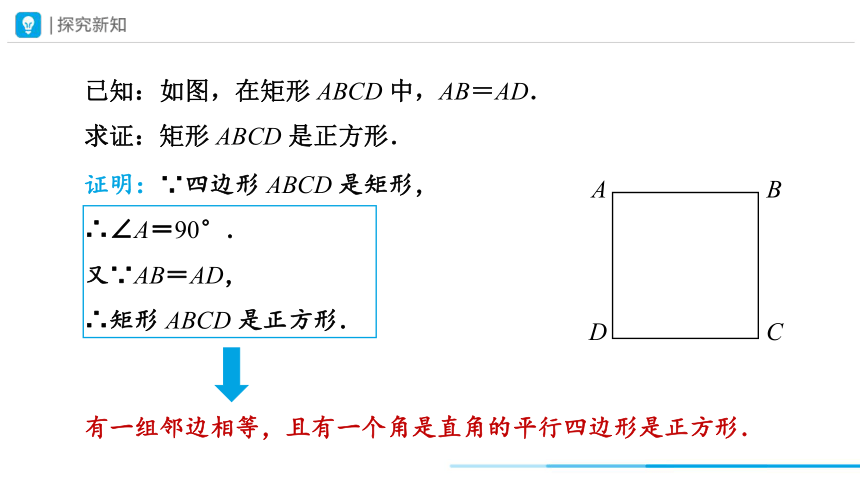
已知:如图,在矩形 ABCD 中,AB=AD.
求证:矩形 ABCD 是正方形.
证明:∵四边形 ABCD 是矩形,
∴∠A=90°.
又∵AB=AD,
∴矩形 ABCD 是正方形.
有一组邻边相等,且有一个角是直角的平行四边形是正方形.
A
B
C
D
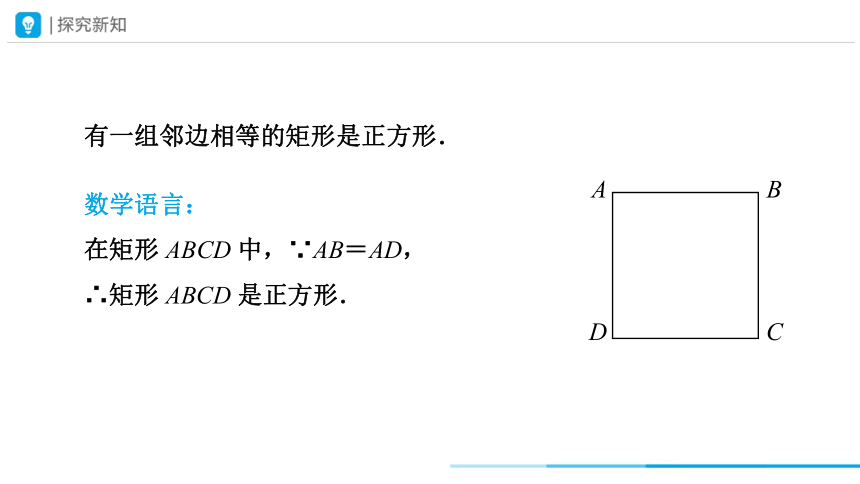
有一组邻边相等的矩形是正方形.
数学语言:
在矩形 ABCD 中,∵AB=AD,
∴矩形 ABCD 是正方形.
A
B
C
D
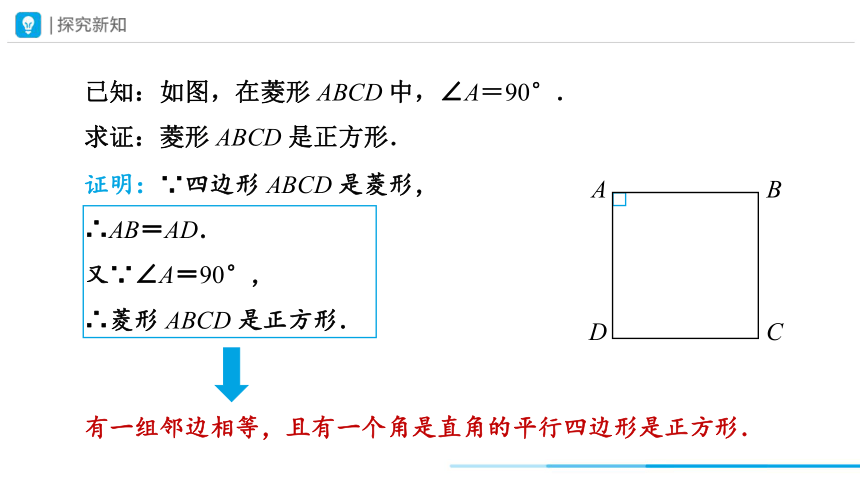
证明:∵四边形 ABCD 是菱形,
∴AB=AD.
又∵∠A=90°,
∴菱形 ABCD 是正方形.
已知:如图,在菱形 ABCD 中,∠A=90°.
求证:菱形 ABCD 是正方形.
A
B
C
D
有一组邻边相等,且有一个角是直角的平行四边形是正方形.
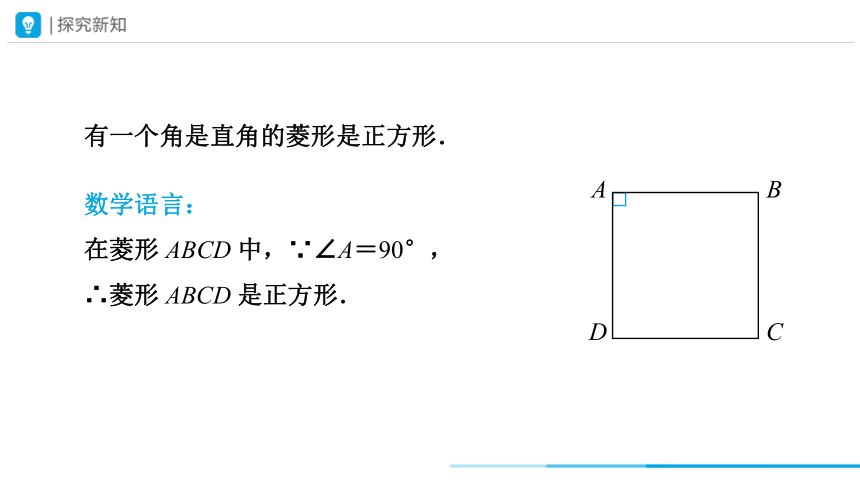
有一个角是直角的菱形是正方形.
数学语言:
在菱形 ABCD 中,∵∠A=90°,
∴菱形 ABCD 是正方形.
A
B
C
D
矩形的对角线具有什么性质?正方形的对角线具有什么样的性质?
思考
对角线相等且互相平分
对角线相等且互相垂直平分
添加对角线互相垂直
能否得到正方形?
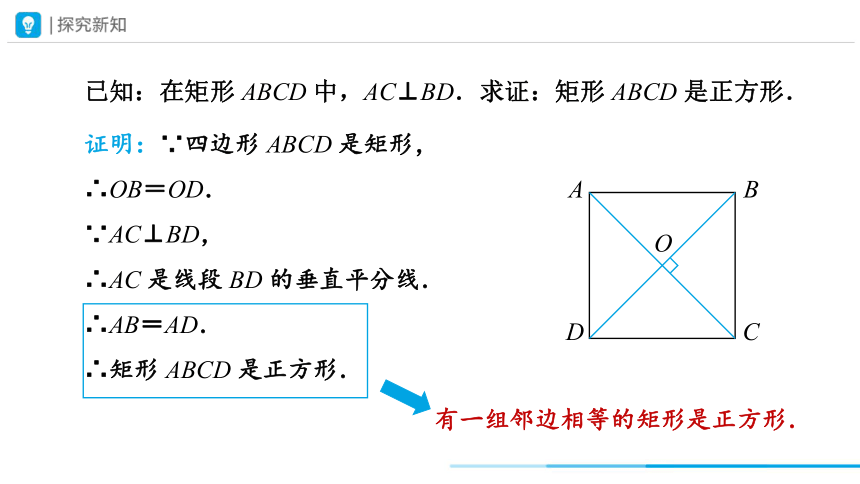
证明:∵四边形 ABCD 是矩形,
∴OB=OD.
∵AC⊥BD,
∴AC 是线段 BD 的垂直平分线.
∴AB=AD.
∴矩形 ABCD 是正方形.
已知:在矩形 ABCD 中,AC⊥BD.求证:矩形 ABCD 是正方形.
A
B
C
D
O
有一组邻边相等的矩形是正方形.
对角线互相垂直的矩形是正方形.
数学语言:
在矩形 ABCD 中,∵AC⊥BD,
∴矩形 ABCD 是正方形.
A
B
C
D
O
思考
菱形的对角线有什么性质?正方形的对角线有什么样的性质?
对角线互相垂直平分
对角线相等且互相垂直平分
添加对角线相等
能否得到正方形?
已知:在菱形 ABCD 中,AC=BD.求证:四边形 ABCD 是正方形.
证明:∵四边形 ABCD 是菱形,
∴OA=OC,OB=OD,AC⊥BD.
∵AC=BD,∴OA=OB=OC=OD.
∴△AOB,△BOC 是等腰直角三角形.
∴∠ABO=∠CBO=45°.
∴∠ABC=90°.
∴菱形 ABCD 是正方形.
A
B
C
D
O
有一个角是直角的菱形是正方形.
对角线相等的菱形是正方形.
数学语言:
在菱形 ABCD 中,∵AC=BD,
∴菱形 ABCD 是正方形.
A
B
C
D
O
例1 下列命题正确的是( ).
A.四个角都相等的四边形是正方形
B.四条边都相等的四边形是正方形
C.对角线互相垂直的矩形是正方形
D.对角线相等的平行四边形是正方形
矩形
菱形
矩形
C
A
B
C
D
E
F
例2 如图,等边三角形 AEF 的顶点 E,F 在矩形 ABCD 的边 BC,CD上,且∠CEF=45°.求证:矩形 ABCD 是正方形.
分析:先证明 △AEB≌△AFD 得到 AB=AD,再根据“有一组邻边相等的矩形是正方形”得出结论.
A
B
C
D
E
F
证明:∵四边形 ABCD 是矩形,∴∠B=∠C=∠D=90°.
∵△AEF 是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=45°.
∴∠AFD=∠AEB=180°-45°-60°=75°.
∴△AEB≌△AFD.
∴AB=AD.
∴矩形 ABCD 是正方形.
例3 如图,在矩形 ABCD 中,BE 平分∠ABC,CE 平分∠DCB,BF∥CE,CF∥BE.求证:四边形 BECF 是正方形.
A
B
C
D
E
F
证明:∵BF∥CE,CF∥BE,
∴四边形 BECF 是平行四边形.
∵四边形 ABCD 是矩形,
∴∠ABC=∠DCB=90°.
又∵BE 平分∠ABC,CE 平分∠DCB,
A
B
C
D
E
F
∴∠EBC= ∠ABC=45°,∠ECB= ∠DCB=45°.
∴∠EBC=∠ECB.
∴EB=EC.
∴平行四边形 BECF 是菱形.
又∵∠EBC=∠ECB=45°,
∴∠BEC=90°.
∴菱形 BECF 是正方形.
正方形的判定
定义法
对角线
有一组邻边相等,且有一个角是直角的平行四边形是正方形
对角线互相垂直的矩形是正方形
对角线相等的菱形是正方形
边
有一组邻边相等的矩形是正方形
角
有一个角是直角的菱形是正方形
18.2.3 正方形
(第2课时)
2.正方形的性质:
1.正方形的定义:
有一组邻边相等,且有一个角是直角的平行四边形是正方形.
(1)边:四条边相等.
(2)角:四个角都是直角.
(3)对角线:对角线相等,且互相垂直平分.
(4)对称性:正方形是轴对称图形,有四条对称轴,分别是对边中点所在的直线以及两条对角线所在的直线.
由正方形的定义可知,有一组邻边相等,且有一个角是直角的平行四边形是正方形.除此之外,还有没有其他判定方法呢?
上节课,我们学过:
(1)有一组邻边相等的矩形是正方形.
(2)有一个角是直角的菱形是正方形.
你能分别给出证明吗?
已知:如图,在矩形 ABCD 中,AB=AD.
求证:矩形 ABCD 是正方形.
证明:∵四边形 ABCD 是矩形,
∴∠A=90°.
又∵AB=AD,
∴矩形 ABCD 是正方形.
有一组邻边相等,且有一个角是直角的平行四边形是正方形.
A
B
C
D
有一组邻边相等的矩形是正方形.
数学语言:
在矩形 ABCD 中,∵AB=AD,
∴矩形 ABCD 是正方形.
A
B
C
D
证明:∵四边形 ABCD 是菱形,
∴AB=AD.
又∵∠A=90°,
∴菱形 ABCD 是正方形.
已知:如图,在菱形 ABCD 中,∠A=90°.
求证:菱形 ABCD 是正方形.
A
B
C
D
有一组邻边相等,且有一个角是直角的平行四边形是正方形.
有一个角是直角的菱形是正方形.
数学语言:
在菱形 ABCD 中,∵∠A=90°,
∴菱形 ABCD 是正方形.
A
B
C
D
矩形的对角线具有什么性质?正方形的对角线具有什么样的性质?
思考
对角线相等且互相平分
对角线相等且互相垂直平分
添加对角线互相垂直
能否得到正方形?
证明:∵四边形 ABCD 是矩形,
∴OB=OD.
∵AC⊥BD,
∴AC 是线段 BD 的垂直平分线.
∴AB=AD.
∴矩形 ABCD 是正方形.
已知:在矩形 ABCD 中,AC⊥BD.求证:矩形 ABCD 是正方形.
A
B
C
D
O
有一组邻边相等的矩形是正方形.
对角线互相垂直的矩形是正方形.
数学语言:
在矩形 ABCD 中,∵AC⊥BD,
∴矩形 ABCD 是正方形.
A
B
C
D
O
思考
菱形的对角线有什么性质?正方形的对角线有什么样的性质?
对角线互相垂直平分
对角线相等且互相垂直平分
添加对角线相等
能否得到正方形?
已知:在菱形 ABCD 中,AC=BD.求证:四边形 ABCD 是正方形.
证明:∵四边形 ABCD 是菱形,
∴OA=OC,OB=OD,AC⊥BD.
∵AC=BD,∴OA=OB=OC=OD.
∴△AOB,△BOC 是等腰直角三角形.
∴∠ABO=∠CBO=45°.
∴∠ABC=90°.
∴菱形 ABCD 是正方形.
A
B
C
D
O
有一个角是直角的菱形是正方形.
对角线相等的菱形是正方形.
数学语言:
在菱形 ABCD 中,∵AC=BD,
∴菱形 ABCD 是正方形.
A
B
C
D
O
例1 下列命题正确的是( ).
A.四个角都相等的四边形是正方形
B.四条边都相等的四边形是正方形
C.对角线互相垂直的矩形是正方形
D.对角线相等的平行四边形是正方形
矩形
菱形
矩形
C
A
B
C
D
E
F
例2 如图,等边三角形 AEF 的顶点 E,F 在矩形 ABCD 的边 BC,CD上,且∠CEF=45°.求证:矩形 ABCD 是正方形.
分析:先证明 △AEB≌△AFD 得到 AB=AD,再根据“有一组邻边相等的矩形是正方形”得出结论.
A
B
C
D
E
F
证明:∵四边形 ABCD 是矩形,∴∠B=∠C=∠D=90°.
∵△AEF 是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=45°.
∴∠AFD=∠AEB=180°-45°-60°=75°.
∴△AEB≌△AFD.
∴AB=AD.
∴矩形 ABCD 是正方形.
例3 如图,在矩形 ABCD 中,BE 平分∠ABC,CE 平分∠DCB,BF∥CE,CF∥BE.求证:四边形 BECF 是正方形.
A
B
C
D
E
F
证明:∵BF∥CE,CF∥BE,
∴四边形 BECF 是平行四边形.
∵四边形 ABCD 是矩形,
∴∠ABC=∠DCB=90°.
又∵BE 平分∠ABC,CE 平分∠DCB,
A
B
C
D
E
F
∴∠EBC= ∠ABC=45°,∠ECB= ∠DCB=45°.
∴∠EBC=∠ECB.
∴EB=EC.
∴平行四边形 BECF 是菱形.
又∵∠EBC=∠ECB=45°,
∴∠BEC=90°.
∴菱形 BECF 是正方形.
正方形的判定
定义法
对角线
有一组邻边相等,且有一个角是直角的平行四边形是正方形
对角线互相垂直的矩形是正方形
对角线相等的菱形是正方形
边
有一组邻边相等的矩形是正方形
角
有一个角是直角的菱形是正方形
