第五章 一元函数的导数及其应用章末小结复习课
文档属性
| 名称 | 第五章 一元函数的导数及其应用章末小结复习课 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-17 19:50:44 | ||
图片预览








文档简介
(共27张PPT)
第五章 一元函数的导数及其应用
章末复习小结
人教A版(2019)
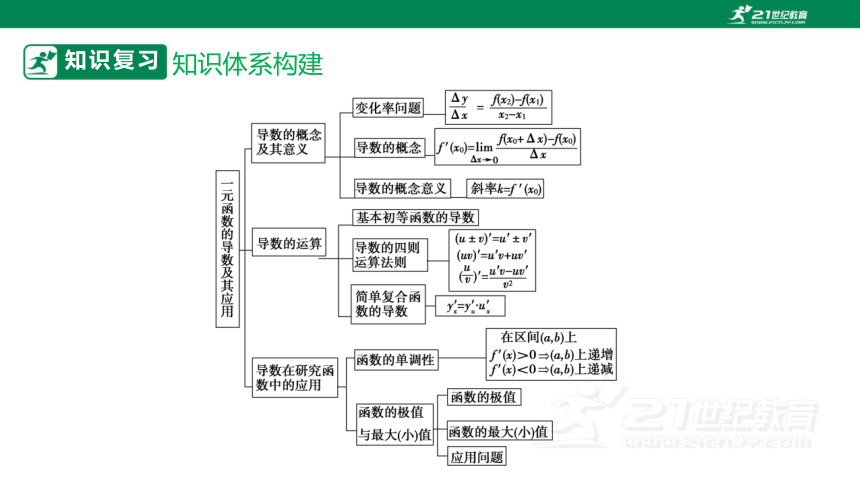
知识复习
知识体系构建
知识梳理
基本初等函数的导数
原函数 导函数
1.若f (x)=c(c为常数),
则f '(x)=0;
2.若f (x)=(α∈Q,且α≠0),
则f '(x)=;
3.若f (x)=,
则f '(x)=;
4.若f (x)=,
则f '(x)=;
5.若f (x)=(a>0,且a≠1),
则f '(x)=;
特别地,若f (x)=,
则f '(x)=;
6.若f (x)=(a>0,且a≠1),
则f '(x)=;
特别地,若f (x)=,
则f '(x)=.
题型探究
题型1:导数的几何意义及运算
1.本部分内容涉及导数的几何意义、基本初等函数求导、导数的四则运算法则、复合函数求导,主要考查切线方程及切点,与切线平行、垂直问题,处理此类问题一般结合函数的切线转化为点到直线的距离,平行线间的距离问题,然后再研究最值问题.
2.通过求切线方程的有关问题,培养数学运算、数学抽象等核心素养和转化化归数学思想.
题型探究
【例1】⑴已知f (x)=tan x,则f ′=( )
A. B. C. D.4
⑵已知f (x)=xex+3sin x,则曲线y=f (x)在点(0,f (0))处的切线方程为( )
A.y=x B.y=3x C.y=2x D.y=4x
⑶(2024·新高考Ⅰ卷)若曲线y=ex+x在点(0,1)处的切线也是曲线y=ln (x+1)+a的切线,则a=________.
题型1:导数的几何意义及运算
题型探究
解:
⑴∵f (x)=tan x=,
∴f ′.故选C.
题型1:导数的几何意义及运算
∴f ′(x)=,
⑵∵f (x)=xex+3sin x,
∴f (0)=0,f ′(x)=ex+xex+3cos x,
∴切线的斜率k=f ′(0)=1+3=4,
∴曲线y=f (x)在点(0,f (0))处的切线方程为y=4x.故选D.
题型探究
解:
⑶由y=ex+x得y′=ex+1,
∴曲线y=ex+x在点(0,1)处的切线方程为y=2x+1.
题型1:导数的几何意义及运算
∴y′|x=0=e0+1=2,
由y=ln (x+1)+a得y′=,
由两曲线有公切线得y′==2,解得x0=-,
则切点为,
设切线与曲线y=ln (x+1)+a相切的切点为(x0,ln (x0+1)+a),
切线方程为y=2+a+ln =2x+1+a-ln 2.
根据两切线重合,所以a-ln 2=0,解得a=ln 2.
初试身手
1.⑴(2023·全国甲卷)曲线y=在点处的切线方程为( )
A.y=x B.y=xC.y=x+ D.y=x+
⑵(2022·新高考Ⅰ卷)若曲线y=(x+a)ex有两条过坐标原点的切线,则a的取值范围是_______________.
解:
⑴由题意可知y′=,
∴曲线y=在点处的切线方程为y-(x-1),
即y=.故选C.
则曲线y=在点处的切线斜率k=,
初试身手
1.⑴(2023·全国甲卷)曲线y=在点处的切线方程为( )
A.y=x B.y=xC.y=x+ D.y=x+
⑵(2022·新高考Ⅰ卷)若曲线y=(x+a)ex有两条过坐标原点的切线,则a的取值范围是_______________.
解:
⑵∵y=(x+a)ex,∴y′=(x+1+a)ex,
∴切线方程为(x-x0),
∵切线过原点,∴(-x0),
设切点为(x0,y0),则y0=,切线斜率k=,
整理得+ax0-a=0,
∵切线有两条,∴Δ=a2+4a>0,解得a<-4或a>0,
∴a的取值范围是(-∞,-4)∪(0,+∞).
题型探究
题型2:导数与函数的单调性
1.借助导数研究函数的单调性,尤其是研究含有ln x,ex等线性函数(或复合函数)的单调性,是近几年高考的一个重点.其特点是f ′(x)的符号一般由二次函数来确定,经常同一元二次方程、一元二次不等式结合,融分类讨论、数形结合于一体.
2.通过利用导数判断函数的单调性,培养直观想象、数学运算等核心素养.
题型探究
【例2】已知函数f (x)=e2x+(a+2)ex+ax,讨论f (x)的单调性.
解:
∵函数f (x)的定义域为R,f ′(x)=2e2x+(a+2)ex+a=(2ex+a).
①当a≥0时,f ′(x)>0,f (x)在R上单调递增,
②当a<0时,令f ′(x)=0,则x=ln ,
题型2:导数与函数的单调性
当x∈时,f ′(x)<0,f (x)单调递减,
当x∈时,f ′(x)>0,f (x)单调递增.
综上,当a≥0时,f (x)在R上单调递增;当a<0时,f (x)在上单调递减,在上单调递增.
初试身手
2.⑴已知函数f(x)=x2-5x+2ln x,则函数f(x)的单调递减区间是( )
A.(0,)和(1,+∞) B.(0,1)和(2,+∞) C.(0,)和(2,+∞) D.(,2)
解:
⑴∵f(x)=x2-5x+2ln x,其定义域为{x|x>0},
∴f ′(x)=2x-5+.
令f ′(x)=0,可得x1=,x2=2.
∴f(x)的单调递减区间为(,2),故选D.
当x∈(,2)时,f ′(x)<0,
初试身手
2.⑵(2023·新高考Ⅱ卷)已知函数f (x)=aex-ln x在区间(1,2)单调递增,则a的最小值为( )
A.e2 B.e C.e-1 D.e-2
解:
⑵∵f (x)=aex-ln x,∴f ′(x)=aex-,
又∵f (x)=aex-ln x在区间(1,2)单调递增,
∴f ′(x)≥0在(1,2)恒成立,
∴在(1,2)上,g(x)>g(1)=e,
即aex-≥0在(1,2)恒成立,
易知a>0,则0<≤xex在(1,2)恒成立.
设g(x)=xex,则g′(x)=(x+1)ex,
当x∈(1,2)时,g′(x)>0,g(x)单调递增,
∴≤e,即a≥=e-1,故选C.
题型探究
题型3:导数与函数的极值、最值
1.极值和最值是两个不同的概念,前者是函数的“局部”性质,而后者是函数的“整体”性质.另外函数有极值未必有最值,反之亦然.
2.判断函数“极值”是否存在时,务必把握以下原则:
⑴确定函数f (x)的定义域;
⑵解方程f ′(x)=0的根;
⑶检验f ′(x)=0的根的两侧f ′(x)的符号:
若左正右负,则f (x)在此根处取得极大值;若左负右正,则f (x)在此根处取得极小值.
题型探究
【例3】已知函数f (x)=ln x-(m∈R).
⑴当m=-2时,求函数f (x)的单调区间和极值;
⑵若函数f (x)在区间[1,e]上取得最小值4,求m的值.
题型3:导数与函数的极值、最值
解:
⑴当m=-2时,f (x)=ln x+(x>0),
则f ′(x)=,
∴当x∈(0,2)时,f ′(x)<0,f (x)单调递减,
当x∈(2,+∞)时,f ′(x)>0,f (x)单调递增,
∴f (x)的单调递增区间为(2,+∞),单调递减区间为(0,2),极小值为f (2)=ln 2+1,无极大值.
题型探究
【例3】已知函数f (x)=ln x-(m∈R).
⑴当m=-2时,求函数f (x)的单调区间和极值;
⑵若函数f (x)在区间[1,e]上取得最小值4,求m的值.
题型3:导数与函数的极值、最值
解:
⑵f ′(x)=,令f ′(x)=0,则x=-m,
①当-m≤1,即m≥-1时,f ′(x)≥0,x∈[1,e],
∴f (x)在[1,e]上单调递增,f (x)min=f (1)=-m=4,
解得m=-4,不满足m≥-1,故舍去.
∴f (x)min=f (-m)=ln (-m)+1=4,
②当1<-m<e,即-e<m<-1时,x∈(1,-m)时,f ′(x)<0,f (x)单调递减,x∈(-m,e)时,f ′(x)>0,f (x)单调递增,
.
解得m=-e3,不满足-e<m<-1,故舍去.
③当-m≥e,即m≤-e时,f ′(x)≤0,x∈[1,e],f (x)在[1,e]上单调递减,f (x)min=
f (e)=1-=4,解得m=-3e,满足m≤-e.
综上,m的值为-3e.
初试身手
解:
3.已知函数f(x)=xlnx.
⑴求f(x)的最小值;
⑵若对所有的x∈[1,+∞)都有f(x)≥ax-1,求实数a的取值范围.
∴当x=时,f(x)取得最小值-.
令f ′(x)=0,解得x=,
⑴∵f(x)的定义域为(0,+∞),f ′(x)=1+ln x.
∴当x∈(0,)时,f ′(x)<0,f(x)在上单调递减;当x∈(,+∞)时,f ′(x)>0,f(x)在上单调递增.
初试身手
解:
3.已知函数f(x)=xlnx.
⑴求f(x)的最小值;
⑵若对所有的x∈[1,+∞)都有f(x)≥ax-1,求实数a的取值范围.
∴g(x)是[1,+∞)上的增函数,g(x)的最小值是g(1)=1,
令g(x)=,则g′(x)=,
∵x∈[1,+∞),g′(x)≥0
∴a的取值范围是(-∞,1].
⑵依题意,得f(x)≥ax-1在[1,+∞)上恒成立,
即不等式a≤对于x∈[1,+∞)恒成立.
题型探究
【例4】已知函数f(x)=.
⑴若b=0,且f ′(x)≥0,求a的最小值;
⑵证明:曲线y=f(x)是中心对称图形;
⑶若f(x)>-2当且仅当1题型4:与导数有关的综合性问题
解:
⑴若b=0,则f(x)=,x∈(0,2),
f ′(x)=,
∴-a≤,x∈(0,2),
∵f ′(x)≥0,
∴-a≤.
∵0∴,即x=1时,=2.
∴-a≤2,a≥-2,则a的最小值为-2.
题型探究
【例4】已知函数f(x)=.
⑴若b=0,且f ′(x)≥0,求a的最小值;
⑵证明:曲线y=f(x)是中心对称图形;
⑶若f(x)>-2当且仅当1题型4:与导数有关的综合性问题
解:
⑵对 x∈(0,2),则x-2∈(0,2),
∴f(2-x)=,
f(x)+f(2-x)=2a,
∴点(x,f(x))与点(2-x,f(2-x))关于点(1,a)对称.
则曲线y=f(x)关于点(1,a)中心对称.
⑶由曲线y=f(x)关于点(1,a)中心对称,f(x)>-2当且仅当1∴x=1是的f(x)=-2的解,
∴f(1)=a=-2,f(x)=.
题型探究
【例4】已知函数f(x)=.
⑴若b=0,且f ′(x)≥0,求a的最小值;
⑵证明:曲线y=f(x)是中心对称图形;
⑶若f(x)>-2当且仅当1题型4:与导数有关的综合性问题
解:
f(1)=a=-2,f(x)=.
∴f ′(x)=,
①当b≥-时,f ′(x)≥0,f(x)在(1,2)单调递增,
∴f(x)>-2=f(1),当且仅当1令f ′(x)=0,即-3bx2+6bx+2=0, >0,有两根,设为x1,x2,
②当b<-时,f ′(x)=,
∵ x1+x2=2,,
∴在(1,x0)上递减,f(x)∴x1<1综上,b的取值范围为[-,+∞).
初试身手
解:
4.函数f (x)=x+ax2+b ln x的图象在点P(1,0)处的切线斜率为2.
⑴求a,b的值;
⑵证明:f (x)≤2x-2对任意正实数x恒成立.
⑴由题设可知f (x)的定义域为(0,+∞),f ′(x)=1+2ax+,
∴f (1)=1+a=0,f ′(1)=1+2a+b=2,
⑵证明:由(1)知f (x)=x-x2+3ln x(x>0),
∵曲线y=f (x)在点P(1,0)处切线的斜率为2,
解得a=-1,b=3.
设g(x)=2-x-x2+3ln x,x>0,
则g′(x)=-1-2x+=-,
则转化为证明2-x-x2+3ln x≤0对任意正实数x恒成立,
初试身手
解:
4.函数f (x)=x+ax2+b ln x的图象在点P(1,0)处的切线斜率为2.
⑴求a,b的值;
⑵证明:f (x)≤2x-2对任意正实数x恒成立.
∴当0<x<1时,g′(x)>0;当x>1时,g′(x)<0,
∴g(x)在x=1处有最大值g(1)=0,
即2-x-x2+3ln x≤0对任意正实数x恒成立,
∴g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴g(x)≤0对任意正实数x恒成立,
则g′(x)=-1-2x+=-,
即f (x)≤2x-2对任意正实数x恒成立,原命题得证.
作业布置
作业: p104 复习参考题5 第8,18,19题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第五章 一元函数的导数及其应用
章末复习小结
人教A版(2019)
知识复习
知识体系构建
知识梳理
基本初等函数的导数
原函数 导函数
1.若f (x)=c(c为常数),
则f '(x)=0;
2.若f (x)=(α∈Q,且α≠0),
则f '(x)=;
3.若f (x)=,
则f '(x)=;
4.若f (x)=,
则f '(x)=;
5.若f (x)=(a>0,且a≠1),
则f '(x)=;
特别地,若f (x)=,
则f '(x)=;
6.若f (x)=(a>0,且a≠1),
则f '(x)=;
特别地,若f (x)=,
则f '(x)=.
题型探究
题型1:导数的几何意义及运算
1.本部分内容涉及导数的几何意义、基本初等函数求导、导数的四则运算法则、复合函数求导,主要考查切线方程及切点,与切线平行、垂直问题,处理此类问题一般结合函数的切线转化为点到直线的距离,平行线间的距离问题,然后再研究最值问题.
2.通过求切线方程的有关问题,培养数学运算、数学抽象等核心素养和转化化归数学思想.
题型探究
【例1】⑴已知f (x)=tan x,则f ′=( )
A. B. C. D.4
⑵已知f (x)=xex+3sin x,则曲线y=f (x)在点(0,f (0))处的切线方程为( )
A.y=x B.y=3x C.y=2x D.y=4x
⑶(2024·新高考Ⅰ卷)若曲线y=ex+x在点(0,1)处的切线也是曲线y=ln (x+1)+a的切线,则a=________.
题型1:导数的几何意义及运算
题型探究
解:
⑴∵f (x)=tan x=,
∴f ′.故选C.
题型1:导数的几何意义及运算
∴f ′(x)=,
⑵∵f (x)=xex+3sin x,
∴f (0)=0,f ′(x)=ex+xex+3cos x,
∴切线的斜率k=f ′(0)=1+3=4,
∴曲线y=f (x)在点(0,f (0))处的切线方程为y=4x.故选D.
题型探究
解:
⑶由y=ex+x得y′=ex+1,
∴曲线y=ex+x在点(0,1)处的切线方程为y=2x+1.
题型1:导数的几何意义及运算
∴y′|x=0=e0+1=2,
由y=ln (x+1)+a得y′=,
由两曲线有公切线得y′==2,解得x0=-,
则切点为,
设切线与曲线y=ln (x+1)+a相切的切点为(x0,ln (x0+1)+a),
切线方程为y=2+a+ln =2x+1+a-ln 2.
根据两切线重合,所以a-ln 2=0,解得a=ln 2.
初试身手
1.⑴(2023·全国甲卷)曲线y=在点处的切线方程为( )
A.y=x B.y=xC.y=x+ D.y=x+
⑵(2022·新高考Ⅰ卷)若曲线y=(x+a)ex有两条过坐标原点的切线,则a的取值范围是_______________.
解:
⑴由题意可知y′=,
∴曲线y=在点处的切线方程为y-(x-1),
即y=.故选C.
则曲线y=在点处的切线斜率k=,
初试身手
1.⑴(2023·全国甲卷)曲线y=在点处的切线方程为( )
A.y=x B.y=xC.y=x+ D.y=x+
⑵(2022·新高考Ⅰ卷)若曲线y=(x+a)ex有两条过坐标原点的切线,则a的取值范围是_______________.
解:
⑵∵y=(x+a)ex,∴y′=(x+1+a)ex,
∴切线方程为(x-x0),
∵切线过原点,∴(-x0),
设切点为(x0,y0),则y0=,切线斜率k=,
整理得+ax0-a=0,
∵切线有两条,∴Δ=a2+4a>0,解得a<-4或a>0,
∴a的取值范围是(-∞,-4)∪(0,+∞).
题型探究
题型2:导数与函数的单调性
1.借助导数研究函数的单调性,尤其是研究含有ln x,ex等线性函数(或复合函数)的单调性,是近几年高考的一个重点.其特点是f ′(x)的符号一般由二次函数来确定,经常同一元二次方程、一元二次不等式结合,融分类讨论、数形结合于一体.
2.通过利用导数判断函数的单调性,培养直观想象、数学运算等核心素养.
题型探究
【例2】已知函数f (x)=e2x+(a+2)ex+ax,讨论f (x)的单调性.
解:
∵函数f (x)的定义域为R,f ′(x)=2e2x+(a+2)ex+a=(2ex+a).
①当a≥0时,f ′(x)>0,f (x)在R上单调递增,
②当a<0时,令f ′(x)=0,则x=ln ,
题型2:导数与函数的单调性
当x∈时,f ′(x)<0,f (x)单调递减,
当x∈时,f ′(x)>0,f (x)单调递增.
综上,当a≥0时,f (x)在R上单调递增;当a<0时,f (x)在上单调递减,在上单调递增.
初试身手
2.⑴已知函数f(x)=x2-5x+2ln x,则函数f(x)的单调递减区间是( )
A.(0,)和(1,+∞) B.(0,1)和(2,+∞) C.(0,)和(2,+∞) D.(,2)
解:
⑴∵f(x)=x2-5x+2ln x,其定义域为{x|x>0},
∴f ′(x)=2x-5+.
令f ′(x)=0,可得x1=,x2=2.
∴f(x)的单调递减区间为(,2),故选D.
当x∈(,2)时,f ′(x)<0,
初试身手
2.⑵(2023·新高考Ⅱ卷)已知函数f (x)=aex-ln x在区间(1,2)单调递增,则a的最小值为( )
A.e2 B.e C.e-1 D.e-2
解:
⑵∵f (x)=aex-ln x,∴f ′(x)=aex-,
又∵f (x)=aex-ln x在区间(1,2)单调递增,
∴f ′(x)≥0在(1,2)恒成立,
∴在(1,2)上,g(x)>g(1)=e,
即aex-≥0在(1,2)恒成立,
易知a>0,则0<≤xex在(1,2)恒成立.
设g(x)=xex,则g′(x)=(x+1)ex,
当x∈(1,2)时,g′(x)>0,g(x)单调递增,
∴≤e,即a≥=e-1,故选C.
题型探究
题型3:导数与函数的极值、最值
1.极值和最值是两个不同的概念,前者是函数的“局部”性质,而后者是函数的“整体”性质.另外函数有极值未必有最值,反之亦然.
2.判断函数“极值”是否存在时,务必把握以下原则:
⑴确定函数f (x)的定义域;
⑵解方程f ′(x)=0的根;
⑶检验f ′(x)=0的根的两侧f ′(x)的符号:
若左正右负,则f (x)在此根处取得极大值;若左负右正,则f (x)在此根处取得极小值.
题型探究
【例3】已知函数f (x)=ln x-(m∈R).
⑴当m=-2时,求函数f (x)的单调区间和极值;
⑵若函数f (x)在区间[1,e]上取得最小值4,求m的值.
题型3:导数与函数的极值、最值
解:
⑴当m=-2时,f (x)=ln x+(x>0),
则f ′(x)=,
∴当x∈(0,2)时,f ′(x)<0,f (x)单调递减,
当x∈(2,+∞)时,f ′(x)>0,f (x)单调递增,
∴f (x)的单调递增区间为(2,+∞),单调递减区间为(0,2),极小值为f (2)=ln 2+1,无极大值.
题型探究
【例3】已知函数f (x)=ln x-(m∈R).
⑴当m=-2时,求函数f (x)的单调区间和极值;
⑵若函数f (x)在区间[1,e]上取得最小值4,求m的值.
题型3:导数与函数的极值、最值
解:
⑵f ′(x)=,令f ′(x)=0,则x=-m,
①当-m≤1,即m≥-1时,f ′(x)≥0,x∈[1,e],
∴f (x)在[1,e]上单调递增,f (x)min=f (1)=-m=4,
解得m=-4,不满足m≥-1,故舍去.
∴f (x)min=f (-m)=ln (-m)+1=4,
②当1<-m<e,即-e<m<-1时,x∈(1,-m)时,f ′(x)<0,f (x)单调递减,x∈(-m,e)时,f ′(x)>0,f (x)单调递增,
.
解得m=-e3,不满足-e<m<-1,故舍去.
③当-m≥e,即m≤-e时,f ′(x)≤0,x∈[1,e],f (x)在[1,e]上单调递减,f (x)min=
f (e)=1-=4,解得m=-3e,满足m≤-e.
综上,m的值为-3e.
初试身手
解:
3.已知函数f(x)=xlnx.
⑴求f(x)的最小值;
⑵若对所有的x∈[1,+∞)都有f(x)≥ax-1,求实数a的取值范围.
∴当x=时,f(x)取得最小值-.
令f ′(x)=0,解得x=,
⑴∵f(x)的定义域为(0,+∞),f ′(x)=1+ln x.
∴当x∈(0,)时,f ′(x)<0,f(x)在上单调递减;当x∈(,+∞)时,f ′(x)>0,f(x)在上单调递增.
初试身手
解:
3.已知函数f(x)=xlnx.
⑴求f(x)的最小值;
⑵若对所有的x∈[1,+∞)都有f(x)≥ax-1,求实数a的取值范围.
∴g(x)是[1,+∞)上的增函数,g(x)的最小值是g(1)=1,
令g(x)=,则g′(x)=,
∵x∈[1,+∞),g′(x)≥0
∴a的取值范围是(-∞,1].
⑵依题意,得f(x)≥ax-1在[1,+∞)上恒成立,
即不等式a≤对于x∈[1,+∞)恒成立.
题型探究
【例4】已知函数f(x)=.
⑴若b=0,且f ′(x)≥0,求a的最小值;
⑵证明:曲线y=f(x)是中心对称图形;
⑶若f(x)>-2当且仅当1
解:
⑴若b=0,则f(x)=,x∈(0,2),
f ′(x)=,
∴-a≤,x∈(0,2),
∵f ′(x)≥0,
∴-a≤.
∵0
∴-a≤2,a≥-2,则a的最小值为-2.
题型探究
【例4】已知函数f(x)=.
⑴若b=0,且f ′(x)≥0,求a的最小值;
⑵证明:曲线y=f(x)是中心对称图形;
⑶若f(x)>-2当且仅当1
解:
⑵对 x∈(0,2),则x-2∈(0,2),
∴f(2-x)=,
f(x)+f(2-x)=2a,
∴点(x,f(x))与点(2-x,f(2-x))关于点(1,a)对称.
则曲线y=f(x)关于点(1,a)中心对称.
⑶由曲线y=f(x)关于点(1,a)中心对称,f(x)>-2当且仅当1
∴f(1)=a=-2,f(x)=.
题型探究
【例4】已知函数f(x)=.
⑴若b=0,且f ′(x)≥0,求a的最小值;
⑵证明:曲线y=f(x)是中心对称图形;
⑶若f(x)>-2当且仅当1
解:
f(1)=a=-2,f(x)=.
∴f ′(x)=,
①当b≥-时,f ′(x)≥0,f(x)在(1,2)单调递增,
∴f(x)>-2=f(1),当且仅当1
②当b<-时,f ′(x)=,
∵ x1+x2=2,,
∴在(1,x0)上递减,f(x)
初试身手
解:
4.函数f (x)=x+ax2+b ln x的图象在点P(1,0)处的切线斜率为2.
⑴求a,b的值;
⑵证明:f (x)≤2x-2对任意正实数x恒成立.
⑴由题设可知f (x)的定义域为(0,+∞),f ′(x)=1+2ax+,
∴f (1)=1+a=0,f ′(1)=1+2a+b=2,
⑵证明:由(1)知f (x)=x-x2+3ln x(x>0),
∵曲线y=f (x)在点P(1,0)处切线的斜率为2,
解得a=-1,b=3.
设g(x)=2-x-x2+3ln x,x>0,
则g′(x)=-1-2x+=-,
则转化为证明2-x-x2+3ln x≤0对任意正实数x恒成立,
初试身手
解:
4.函数f (x)=x+ax2+b ln x的图象在点P(1,0)处的切线斜率为2.
⑴求a,b的值;
⑵证明:f (x)≤2x-2对任意正实数x恒成立.
∴当0<x<1时,g′(x)>0;当x>1时,g′(x)<0,
∴g(x)在x=1处有最大值g(1)=0,
即2-x-x2+3ln x≤0对任意正实数x恒成立,
∴g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴g(x)≤0对任意正实数x恒成立,
则g′(x)=-1-2x+=-,
即f (x)≤2x-2对任意正实数x恒成立,原命题得证.
作业布置
作业: p104 复习参考题5 第8,18,19题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
