沪教版八年级数学下册 22.2 平行四边形的判定 (含解析)
文档属性
| 名称 | 沪教版八年级数学下册 22.2 平行四边形的判定 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-17 00:00:00 | ||
图片预览




文档简介
22.2 平行四边形的判定
一、单选题
1.不能判定一个四边形是平行四边形的条件是( )
A.一组对边相等,另一组对边平行 B.一组对边平行且相等
C.两条对角线互相平分 D.两组对边分别相等
2.如图给出了四边形的部分数据,若使得四边形为平行四边形,还需要添加的条件可以是( )
A. B. C. D.
3.如图,在四边形中,.若,则的度数为( )
A. B. C. D.
4.用反证法证明命题“已知在中,,则”时,首先应该假设( )
A. B.
C. D.且
5.如图,在平行四边形ABCD中,点E,F分别在边上,连接,添加选项中的条件后不能判定四边形是平行四边形的是( )
A. B. C. D.
6.如图所示,把两张矩形纸条交叉叠放在一起,重合部分构成一个四边形.固定一张纸条,另一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形的周长不变 B.四边形的面积不变
C. D.
7.如图,在中,是上一点,,交于点,,交于点.若,则( )
A. B. C. D.
8.如图,在平行四边形ABCD中,E和F分别是边和上的点,,连接和,已知,,四边形的面积是3,则四边形的面积是( )
A.4.5 B.5 C.6 D.6.5
9.如图,在平行四边形ABCD中,E、F分别为边AB、DC的中点,连接AF、CE、DE、BF、EF,AF与DE交于点G,CE与BF交于点H,则图中共有平行四边形( )
A.3个 B.4个 C.5个 D.6个
10.如图,四边形中,于点E,于点F,交于点C.,连接.以下结论:①;②;③.其中正确的结论个数为( )
A.0个 B.1个 C.2个 D.3个
二、填空题
11.如图,在四边形ABCD中,已知AB∥CD,再添加一个条件 ,则四边形ABCD是平行四边形(图中不再添加辅助线)
12.如图,在四边形中,,若加上,则四边形为平行四边形,现在请你添加一个适当的条件: ,使得四边形为平行四边形.(图中不再添加点和线)
13.对于命题“如图,如果OA=OC,OB≠OD,那么四边形ABCD不是平行四边形”.用反证法证明这个结论时,第一步应假设 .
14.已知三条线段长分别为10,14,20,以其中两条为对角线,剩余一条为边,可以画出 个平行四边形.
15.如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的∠1是68°25′,那么光线与纸板左上方所成的∠2的度数为 .
16.在四边形ABCD中,AC,BD交于点O,且OA=OC,OB=OD,∠ABC=80°,则∠ADC= .
17.如图,,,,图中有 个平行四边形,它们分别是 .
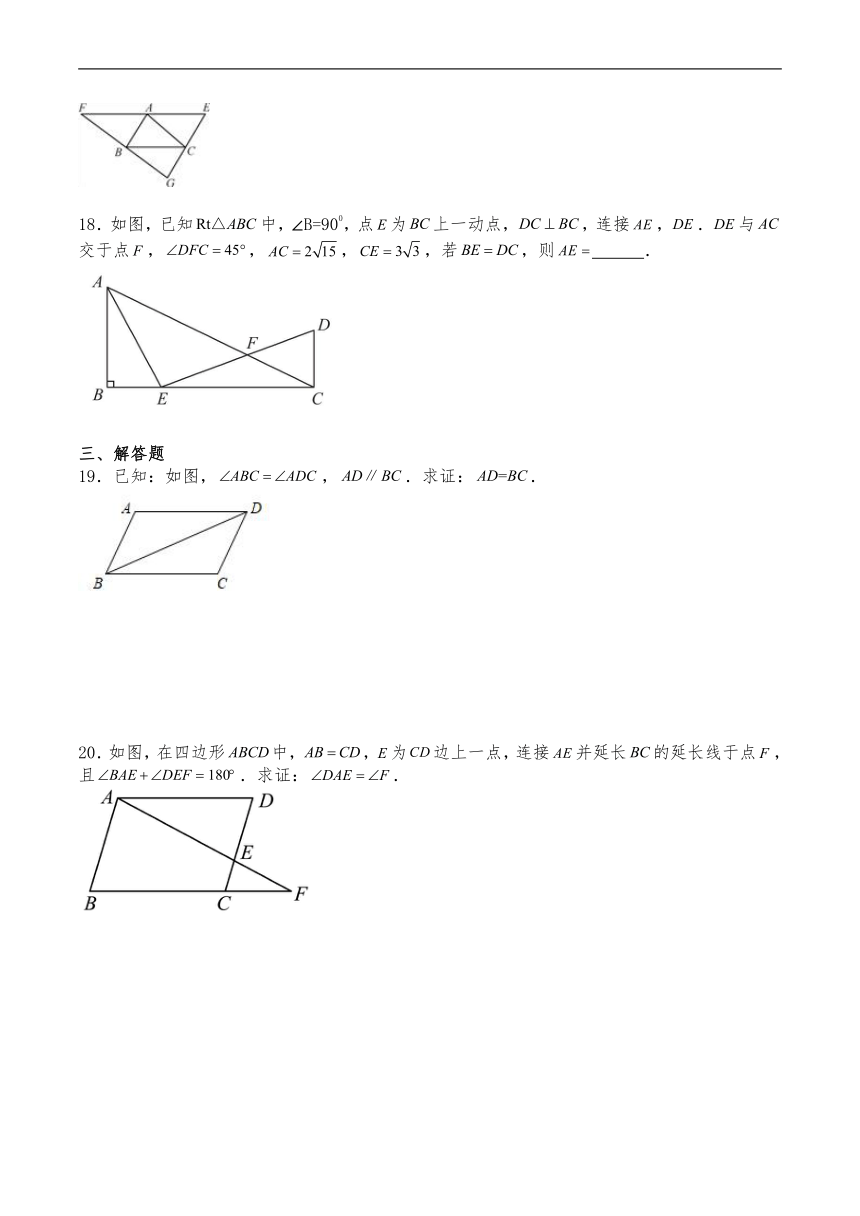
18.如图,已知中,∠B=900,点为上一动点,,连接,.与交于点,,,,若,则 .
三、解答题
19.已知:如图,,.求证:.
20.如图,在四边形中,,为边上一点,连接并延长的延长线于点,且.求证:.
21.如图,在四边形中,AD//BC,点、在上,AE//CF,且.求证:四边形是平行四边形.
22.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.求证:四边形EGFH是平行四边形.
23.已知,点B,D在线段AF上,,且.
(1)求证:;
(2)连接,,求证:四边形是平行四边形.
24.如图,在平行四边形ABCD中,直线,与CD、CB的延长线分别交于点E、F,交AB、AD于G、H.
(1)求证:四边形FBDH为平行四边形;
(2)求证:.
25.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.四边形的四个顶点都是格点,仅用无刻度的直尺在给定网格中完成画图(画图过程用虚线,画图结果用实线).
(1)判断四边形的形状;
(2)在图1中,先在上画点,使,再在上画点,使;
(3)在图2中的上画点,使.
26.已知:如图,在平行四边形中,分别是和的角平分线,交于点E,F连接.
(1)求证:互相平分;
(2)若,求四边形的周长和面积.
27.如图:
(1)如图1,平行四边形ABCD中,于M,于N.求证:.
(2)如图2,平行四边形ABCD中,AC,BD是两条对角线,求证:.
(3)如图3,PT是的中线,已知:,,.求:PT的长度.
28.在平形四边形中,点是对角线的中点,点在边上,的延长线与边交于点,连接、如图1.
(1)求证:四边形是平行四边形;
(2)若,,过点作的垂线,与、、分别交于点、、如图2.
①当,时,求的长;
②求证:.
答案
一、单选题
1.A
【分析】本题考查平行四边形的判定,根据平行四边形的判定方法逐项判断即可.
【解析】解:一组对边相等,另一组对边平行,不能判定一个四边形是平行四边形,故A选项正确;
一组对边平行且相等,能判定一个四边形是平行四边形,故B选项错误;
两条对角线互相平分,能判定一个四边形是平行四边形,故C选项错误;
两组对边分别相等,能判定一个四边形是平行四边形,故D选项错误;
故选A.
2.B
【分析】根据平行四边形的判定定理添加条件即可求解.
【解析】解:∵在四边形中,,
∴,
∴根据一组对边平行且相等的四边形是平行四边形的判定,可添加的条件是:.
故选:B.
3.B
【解析】略
4.】A
【分析】根据反证法的步骤中,第一步是假设结论不成立,反面成立解答.
【解析】解:用反证法证明命题“已知在中,,则”时,首先应该假设.
故选:A
5.D
【分析】根据平行四边形的性质,平行四边形的判定依次进行判断即可得.
【解析】解:∵四边形为平行四边形,
∴,
∵,
∴四边形是平行四边形,
故选项A说法正确,不符合题意;
∵四边形为平行四边形,
∴,
∵,
∴四边形是平行四边形,
故选项B说法正确,不符合题意;
∵四边形为平行四边形,
∴,,
∵,
∴
∴四边形是平行四边形,
故选项C说法正确,不符合题意;
∵四边形为平行四边形,
∴,,
由不能判定四边形是平行四边形,
故选项D说法错误,符合题意;
故选:D.
6.D
【分析】本题考查了平行四边形的判定和性质,由平行四边形的性质进行判断,即可得到答案,解题的关键是掌握平行四边形的判定和性质.
【解析】解:由题意可知,,,
∴四边形是平行四边形,
∴,故符合题意,
随着一张纸条在转动过程中,不一定等于,四边形周长、面积都会改变,
故不符合题意,
故选:.
7.D
【分析】根据已知判定四边形是平行四边形,得到,再根据三角形内角和定理求解.
【解析】解:∵,,
∴四边形是平行四边形,
∴,
∵,
∴,
故选:D.
8.C
【分析】先证明四边形是平行四边形,得,即可推导出,则四边形是平行四边形,设与之间的距离为h,,由,得,于是得到问题的答案.
【解析】解:∵四边形是平行四边形,
∴,,
∵,
∴四边形是平行四边形,
∴,
∴,
∴,
∵,,
∴四边形是平行四边形,
设与之间的距离为h,
∵四边形的面积是3,
∴,
∵,
∴,
故选:C.
9.D
【分析】根据四边形ABCD是平行四边形,得到AB=CD,AB∥CD,根据E、F分别为边AB、DC的中点,得到AE=BE= AB,CF=DF= CD,推出AE=DF =CF=BE,推出四边形ADFE,AFCE,EDFB,EFCB都是平行四边形,得到AE∥CE,DE∥BF,推出四边形EGFH是平行四边形,至此,连原来的平行四边形共有6个.
【解析】∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵E、F分别为边AB、DC的中点,
∴AE=BE= AB,CF=DF= CD,
∴AE=DF,AE=CF,BE=CF,BE=DF,
∴四边形ADFE,AFCE,EDFB,EFCB都是平行四边形,
∴AE∥CE,DE∥BF,
∴四边形EGFH是平行四边形,
故平行四边形共有6个.
故选D.
10.C
【分析】根据可判定①,用反证法证明②,根据证得,得到可判断③.
【解析】解:∵于点E,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,故①正确;
用反证法证明②,
假设,
则有为等腰三角形,F为的中点,
又,可证得,与题设不符;
由(1)知,
∴,
连接,
∵
∴四边形为平行四边形,
∴,
∴,
∴,
∵
∴,
∴,故③正确;
故正确的个数有2个.
故选:C.
二、填空题
11.AB=CD(或AD∥BC)
【分析】根据平行四边形的判定定理添加条件即可.
【解析】解:已知AB∥CD,
∵一组对边平行且相等的四边形是平行四边形;两组对边分别平行的四边形是平行四边形,
∴可添加AB=CD或AD∥BC,
故答案为AB=CD(或AD∥BC).
12.
【解析】连结,交于点,
∵,,
∴四边形是平行四边形,
∴,,
∵,
∴,
∴四边形为平行四边形.
13.四边形ABCD是平行四边形
【分析】用反证法证明命题的真假,先假设命题的结论不成立,从这个结论出发,经过推理论证,得出矛盾;由矛盾判定假设不正确,从而肯定命题的结论正确.
【解析】解:用反证法证明某个命题的结论“四边形ABCD不是平行四边形”时,第一步应假设四边形ABCD是平行四边形,
故答案为:四边形ABCD是平行四边形.
14.2
【分析】根据平行四边形性质得出OA=OC= AC,BO =OD=BD,分为三种情况:①AC=10,BD=14,AB=20时,②AC=10,BD=20,AB=14时,③AC=20,BD=14,AB=10时,求出AO和BO的值,根据三角形的三边关系定理看看△AOB是否存在即可.
【解析】解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,BO=OD=BD,
分为三种情况:
①AC=10,BD=14,AB=20时,AO=5,BO=7,
则5+7<20,不符合三角形三边关系定理;不能组成平行四边形;
②AC=10,BD=20,AB=14时,AO=5,BO=10,
则5+10>14,符合三角形三边关系定理;能组成平行四边形;
③AC=20,BD=14,AB=10时,AO=10,BO=7,
则7+10>10,符合三角形三边关系定理;能组成平行四边形;
可以画出不同形状的平行四边形的个数是2,
故答案为2.
15.68°25′
【分析】先证明四边形ABCD是平行四边形,进而即可求解.
【解析】因为AB∥CD,AD∥BC,所以四边形ABCD是平行四边形,所以∠2=∠1=68°25′,
故答案为68°25′.
16.80°
【解析】略
17. 3 、、
【分析】由平行四边形的判定即可得出结论.
【解析】解:图中有3个平行四边形,分别为、、,理由如下:
,,,
四边形、四边形、四边形是平行四边形.
故答案为3, 、、.
18.
【分析】延长,过点E作,交延长线于点G,连接,可证明,有,;再证明四边形为平行四边形,,
;由勾股定理可求得的长,从而可求得的长,最后由勾股定理即可求得结果.
【解析】解:延长,过点E作,交延长线于点G,连接,如图,
则,
∵∠B=900,,
∴,
∴,
∵,
∴,
∴,;
∵,
∴,
∵,
∴,
∵∠B=900,,
∴,
∴四边形为平行四边形,
∴,;
由勾股定理得:;
在中,由勾股定理得;
∴,
∴,
在中,由勾股定理得:,
故答案为:.
三、解答题
19.证明:∵,
∴,
又∵,
∴,
即:,
∴,
∴四边形为平行四边形,
∴.
20.证明:∵,,
∴,
∴AB∥CD,
∵,
∴四边形是平行四边形,
∴AD∥CB,
∴.
21.∵AD//BC
(两直线平行,内错角相等)
又∵AE//CF
(两直线平行,内错角相等)
在△ADE和△CBF中,
四边形是平行四边形(一组对边平行且相等的四边形是平行四边形)
22.证明:∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE//HF,
又∵GE=HF,
∴四边形EGFH是平行四边形
23.(1)证明:如图所示:
∵,
∴.
∴.
∵,
∴.
在和△FDE中,
∵,
∴.
(2)连接,,
由(1)知,
∴,.
∴.
∴四边形是平行四边形.
24.(1)∵四边形ABCD为平行四边形,
∴,
∴,
∴四边形FBDH为平行四边形,
(2)∵四边形FBDH为平行四边形,
∴,
∵,,
∴四边形BDEG为平行四边形,
∴,
∴,
∴,
∴.
25.(1)解:∵,,
∴四边形是平行四边形.
(2)解:如图1中,点E,点F即为所求;
根据格点特点可知,,,
∴,
∴;
∵四边形为平行四边形,
∴,,
∴,,
∴,
∴.
(3)解:如图2中,点G即为所求.
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
26.(1)解:∵四边形是平行四边形
∴,
∵分别是和的角平分线
∴
∵,
∴
∴
∴,
∴,
∴即
∵,
∴四边形是平行四边形,
∴互相平分;
(2)∵,
∴△ADE是等边三角形
∵,
∴,
∵,
∴
∴四边形的周长;
过D点作于点G,
在中,,
∴,
∴,
∴,
∴四边形的面积.
27.(1)证明:∵四边形是平行四边形,
∴,
∴,
又∵,
∴,
在和中,,
∴ ,
∴.
(2)证明:作于M,于N,如图所示,
在和中,
根据勾股定理得,,
∴,
同理,在和中,
根据勾股定理得,,
∴,
∴,
联系第一问,易证:,
∴,
∴,
又∵,
∴.
(3)延长PT至S,使得,连接QS,RS,如图所示,
∵PT是的中线,
∴,
∴四边形PQSR为平行四边形,
∴,,
由(2)得,
∴,
解得,
∵ ,
∴.
28.(1)证明:∵在平行四边形中,点是对角线的中点,
∴,,
∴,
在与中,
,
∴,
∴,
又∵,即,
∴四边形是平行四边形.
(2)①解:如图,过点作于点,
∵,,,
∴,
∴,
∵,,
∴,
∴,
∴.
∴的长为.
②证明:∵,,
∴,,
∴,
∵,,
∴,
∴,
∵,,
∴,
∴.
一、单选题
1.不能判定一个四边形是平行四边形的条件是( )
A.一组对边相等,另一组对边平行 B.一组对边平行且相等
C.两条对角线互相平分 D.两组对边分别相等
2.如图给出了四边形的部分数据,若使得四边形为平行四边形,还需要添加的条件可以是( )
A. B. C. D.
3.如图,在四边形中,.若,则的度数为( )
A. B. C. D.
4.用反证法证明命题“已知在中,,则”时,首先应该假设( )
A. B.
C. D.且
5.如图,在平行四边形ABCD中,点E,F分别在边上,连接,添加选项中的条件后不能判定四边形是平行四边形的是( )
A. B. C. D.
6.如图所示,把两张矩形纸条交叉叠放在一起,重合部分构成一个四边形.固定一张纸条,另一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形的周长不变 B.四边形的面积不变
C. D.
7.如图,在中,是上一点,,交于点,,交于点.若,则( )
A. B. C. D.
8.如图,在平行四边形ABCD中,E和F分别是边和上的点,,连接和,已知,,四边形的面积是3,则四边形的面积是( )
A.4.5 B.5 C.6 D.6.5
9.如图,在平行四边形ABCD中,E、F分别为边AB、DC的中点,连接AF、CE、DE、BF、EF,AF与DE交于点G,CE与BF交于点H,则图中共有平行四边形( )
A.3个 B.4个 C.5个 D.6个
10.如图,四边形中,于点E,于点F,交于点C.,连接.以下结论:①;②;③.其中正确的结论个数为( )
A.0个 B.1个 C.2个 D.3个
二、填空题
11.如图,在四边形ABCD中,已知AB∥CD,再添加一个条件 ,则四边形ABCD是平行四边形(图中不再添加辅助线)
12.如图,在四边形中,,若加上,则四边形为平行四边形,现在请你添加一个适当的条件: ,使得四边形为平行四边形.(图中不再添加点和线)
13.对于命题“如图,如果OA=OC,OB≠OD,那么四边形ABCD不是平行四边形”.用反证法证明这个结论时,第一步应假设 .
14.已知三条线段长分别为10,14,20,以其中两条为对角线,剩余一条为边,可以画出 个平行四边形.
15.如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的∠1是68°25′,那么光线与纸板左上方所成的∠2的度数为 .
16.在四边形ABCD中,AC,BD交于点O,且OA=OC,OB=OD,∠ABC=80°,则∠ADC= .
17.如图,,,,图中有 个平行四边形,它们分别是 .
18.如图,已知中,∠B=900,点为上一动点,,连接,.与交于点,,,,若,则 .
三、解答题
19.已知:如图,,.求证:.
20.如图,在四边形中,,为边上一点,连接并延长的延长线于点,且.求证:.
21.如图,在四边形中,AD//BC,点、在上,AE//CF,且.求证:四边形是平行四边形.
22.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.求证:四边形EGFH是平行四边形.
23.已知,点B,D在线段AF上,,且.
(1)求证:;
(2)连接,,求证:四边形是平行四边形.
24.如图,在平行四边形ABCD中,直线,与CD、CB的延长线分别交于点E、F,交AB、AD于G、H.
(1)求证:四边形FBDH为平行四边形;
(2)求证:.
25.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.四边形的四个顶点都是格点,仅用无刻度的直尺在给定网格中完成画图(画图过程用虚线,画图结果用实线).
(1)判断四边形的形状;
(2)在图1中,先在上画点,使,再在上画点,使;
(3)在图2中的上画点,使.
26.已知:如图,在平行四边形中,分别是和的角平分线,交于点E,F连接.
(1)求证:互相平分;
(2)若,求四边形的周长和面积.
27.如图:
(1)如图1,平行四边形ABCD中,于M,于N.求证:.
(2)如图2,平行四边形ABCD中,AC,BD是两条对角线,求证:.
(3)如图3,PT是的中线,已知:,,.求:PT的长度.
28.在平形四边形中,点是对角线的中点,点在边上,的延长线与边交于点,连接、如图1.
(1)求证:四边形是平行四边形;
(2)若,,过点作的垂线,与、、分别交于点、、如图2.
①当,时,求的长;
②求证:.
答案
一、单选题
1.A
【分析】本题考查平行四边形的判定,根据平行四边形的判定方法逐项判断即可.
【解析】解:一组对边相等,另一组对边平行,不能判定一个四边形是平行四边形,故A选项正确;
一组对边平行且相等,能判定一个四边形是平行四边形,故B选项错误;
两条对角线互相平分,能判定一个四边形是平行四边形,故C选项错误;
两组对边分别相等,能判定一个四边形是平行四边形,故D选项错误;
故选A.
2.B
【分析】根据平行四边形的判定定理添加条件即可求解.
【解析】解:∵在四边形中,,
∴,
∴根据一组对边平行且相等的四边形是平行四边形的判定,可添加的条件是:.
故选:B.
3.B
【解析】略
4.】A
【分析】根据反证法的步骤中,第一步是假设结论不成立,反面成立解答.
【解析】解:用反证法证明命题“已知在中,,则”时,首先应该假设.
故选:A
5.D
【分析】根据平行四边形的性质,平行四边形的判定依次进行判断即可得.
【解析】解:∵四边形为平行四边形,
∴,
∵,
∴四边形是平行四边形,
故选项A说法正确,不符合题意;
∵四边形为平行四边形,
∴,
∵,
∴四边形是平行四边形,
故选项B说法正确,不符合题意;
∵四边形为平行四边形,
∴,,
∵,
∴
∴四边形是平行四边形,
故选项C说法正确,不符合题意;
∵四边形为平行四边形,
∴,,
由不能判定四边形是平行四边形,
故选项D说法错误,符合题意;
故选:D.
6.D
【分析】本题考查了平行四边形的判定和性质,由平行四边形的性质进行判断,即可得到答案,解题的关键是掌握平行四边形的判定和性质.
【解析】解:由题意可知,,,
∴四边形是平行四边形,
∴,故符合题意,
随着一张纸条在转动过程中,不一定等于,四边形周长、面积都会改变,
故不符合题意,
故选:.
7.D
【分析】根据已知判定四边形是平行四边形,得到,再根据三角形内角和定理求解.
【解析】解:∵,,
∴四边形是平行四边形,
∴,
∵,
∴,
故选:D.
8.C
【分析】先证明四边形是平行四边形,得,即可推导出,则四边形是平行四边形,设与之间的距离为h,,由,得,于是得到问题的答案.
【解析】解:∵四边形是平行四边形,
∴,,
∵,
∴四边形是平行四边形,
∴,
∴,
∴,
∵,,
∴四边形是平行四边形,
设与之间的距离为h,
∵四边形的面积是3,
∴,
∵,
∴,
故选:C.
9.D
【分析】根据四边形ABCD是平行四边形,得到AB=CD,AB∥CD,根据E、F分别为边AB、DC的中点,得到AE=BE= AB,CF=DF= CD,推出AE=DF =CF=BE,推出四边形ADFE,AFCE,EDFB,EFCB都是平行四边形,得到AE∥CE,DE∥BF,推出四边形EGFH是平行四边形,至此,连原来的平行四边形共有6个.
【解析】∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵E、F分别为边AB、DC的中点,
∴AE=BE= AB,CF=DF= CD,
∴AE=DF,AE=CF,BE=CF,BE=DF,
∴四边形ADFE,AFCE,EDFB,EFCB都是平行四边形,
∴AE∥CE,DE∥BF,
∴四边形EGFH是平行四边形,
故平行四边形共有6个.
故选D.
10.C
【分析】根据可判定①,用反证法证明②,根据证得,得到可判断③.
【解析】解:∵于点E,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,故①正确;
用反证法证明②,
假设,
则有为等腰三角形,F为的中点,
又,可证得,与题设不符;
由(1)知,
∴,
连接,
∵
∴四边形为平行四边形,
∴,
∴,
∴,
∵
∴,
∴,故③正确;
故正确的个数有2个.
故选:C.
二、填空题
11.AB=CD(或AD∥BC)
【分析】根据平行四边形的判定定理添加条件即可.
【解析】解:已知AB∥CD,
∵一组对边平行且相等的四边形是平行四边形;两组对边分别平行的四边形是平行四边形,
∴可添加AB=CD或AD∥BC,
故答案为AB=CD(或AD∥BC).
12.
【解析】连结,交于点,
∵,,
∴四边形是平行四边形,
∴,,
∵,
∴,
∴四边形为平行四边形.
13.四边形ABCD是平行四边形
【分析】用反证法证明命题的真假,先假设命题的结论不成立,从这个结论出发,经过推理论证,得出矛盾;由矛盾判定假设不正确,从而肯定命题的结论正确.
【解析】解:用反证法证明某个命题的结论“四边形ABCD不是平行四边形”时,第一步应假设四边形ABCD是平行四边形,
故答案为:四边形ABCD是平行四边形.
14.2
【分析】根据平行四边形性质得出OA=OC= AC,BO =OD=BD,分为三种情况:①AC=10,BD=14,AB=20时,②AC=10,BD=20,AB=14时,③AC=20,BD=14,AB=10时,求出AO和BO的值,根据三角形的三边关系定理看看△AOB是否存在即可.
【解析】解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,BO=OD=BD,
分为三种情况:
①AC=10,BD=14,AB=20时,AO=5,BO=7,
则5+7<20,不符合三角形三边关系定理;不能组成平行四边形;
②AC=10,BD=20,AB=14时,AO=5,BO=10,
则5+10>14,符合三角形三边关系定理;能组成平行四边形;
③AC=20,BD=14,AB=10时,AO=10,BO=7,
则7+10>10,符合三角形三边关系定理;能组成平行四边形;
可以画出不同形状的平行四边形的个数是2,
故答案为2.
15.68°25′
【分析】先证明四边形ABCD是平行四边形,进而即可求解.
【解析】因为AB∥CD,AD∥BC,所以四边形ABCD是平行四边形,所以∠2=∠1=68°25′,
故答案为68°25′.
16.80°
【解析】略
17. 3 、、
【分析】由平行四边形的判定即可得出结论.
【解析】解:图中有3个平行四边形,分别为、、,理由如下:
,,,
四边形、四边形、四边形是平行四边形.
故答案为3, 、、.
18.
【分析】延长,过点E作,交延长线于点G,连接,可证明,有,;再证明四边形为平行四边形,,
;由勾股定理可求得的长,从而可求得的长,最后由勾股定理即可求得结果.
【解析】解:延长,过点E作,交延长线于点G,连接,如图,
则,
∵∠B=900,,
∴,
∴,
∵,
∴,
∴,;
∵,
∴,
∵,
∴,
∵∠B=900,,
∴,
∴四边形为平行四边形,
∴,;
由勾股定理得:;
在中,由勾股定理得;
∴,
∴,
在中,由勾股定理得:,
故答案为:.
三、解答题
19.证明:∵,
∴,
又∵,
∴,
即:,
∴,
∴四边形为平行四边形,
∴.
20.证明:∵,,
∴,
∴AB∥CD,
∵,
∴四边形是平行四边形,
∴AD∥CB,
∴.
21.∵AD//BC
(两直线平行,内错角相等)
又∵AE//CF
(两直线平行,内错角相等)
在△ADE和△CBF中,
四边形是平行四边形(一组对边平行且相等的四边形是平行四边形)
22.证明:∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE//HF,
又∵GE=HF,
∴四边形EGFH是平行四边形
23.(1)证明:如图所示:
∵,
∴.
∴.
∵,
∴.
在和△FDE中,
∵,
∴.
(2)连接,,
由(1)知,
∴,.
∴.
∴四边形是平行四边形.
24.(1)∵四边形ABCD为平行四边形,
∴,
∴,
∴四边形FBDH为平行四边形,
(2)∵四边形FBDH为平行四边形,
∴,
∵,,
∴四边形BDEG为平行四边形,
∴,
∴,
∴,
∴.
25.(1)解:∵,,
∴四边形是平行四边形.
(2)解:如图1中,点E,点F即为所求;
根据格点特点可知,,,
∴,
∴;
∵四边形为平行四边形,
∴,,
∴,,
∴,
∴.
(3)解:如图2中,点G即为所求.
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
26.(1)解:∵四边形是平行四边形
∴,
∵分别是和的角平分线
∴
∵,
∴
∴
∴,
∴,
∴即
∵,
∴四边形是平行四边形,
∴互相平分;
(2)∵,
∴△ADE是等边三角形
∵,
∴,
∵,
∴
∴四边形的周长;
过D点作于点G,
在中,,
∴,
∴,
∴,
∴四边形的面积.
27.(1)证明:∵四边形是平行四边形,
∴,
∴,
又∵,
∴,
在和中,,
∴ ,
∴.
(2)证明:作于M,于N,如图所示,
在和中,
根据勾股定理得,,
∴,
同理,在和中,
根据勾股定理得,,
∴,
∴,
联系第一问,易证:,
∴,
∴,
又∵,
∴.
(3)延长PT至S,使得,连接QS,RS,如图所示,
∵PT是的中线,
∴,
∴四边形PQSR为平行四边形,
∴,,
由(2)得,
∴,
解得,
∵ ,
∴.
28.(1)证明:∵在平行四边形中,点是对角线的中点,
∴,,
∴,
在与中,
,
∴,
∴,
又∵,即,
∴四边形是平行四边形.
(2)①解:如图,过点作于点,
∵,,,
∴,
∴,
∵,,
∴,
∴,
∴.
∴的长为.
②证明:∵,,
∴,,
∴,
∵,,
∴,
∴,
∵,,
∴,
∴.
