沪教版九年级数学上册 24.3三角形一边的平行线同步测试(含解析)
文档属性
| 名称 | 沪教版九年级数学上册 24.3三角形一边的平行线同步测试(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-17 09:57:03 | ||
图片预览




文档简介
24.3三角形一边的平行线
一、单选题
1.如图,在△ABC中,是边上的中线,是重心.如果,那么线段的长为( )
A.1 B.2 C.3 D.6
2.如图,P是△ABC重心,且经过点P,则的值为( )
A. B. C. D.
3.如图,在△ABC中,,,下列结论正确的是( )
A. B. C. D.
4.如图,在△ABC中,点D在边BC上,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.; B.; C.; D..
5.如图,是△ABC的中线,E是上一点,,的延长线交于F,则的值为( )
A. B. C. D.
6.如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F,连接CD,交EF于点K,则下列说法正确的是( )
A. B.
C. D.
7.如图,在△ABC中,中线相交于点G,下列说法错误的是( )
A.点G为△ABC的重心 B.
C.当△ABC为等边三角形时, D.
8.如图,平行四边形中,连接,在的延长线上取一点,点为的中点,连接,交、分别为点、点,则下列结论错误的是( ).
A. B.
C. D.
9.如图,在中,,点M在边上,线段沿着过M的直线折叠,点C恰巧落在边上的点N处.如果,,那么a与b满足的关系式是( )
A. B. C. D.
10.如图,点D,E,F分别在△ABC的边上,,,,点M是的中点,连接并延长交于点N,的值是( )
A. B. C. D.
二、填空题
11.在中,,点是重心,如果,,那么 .
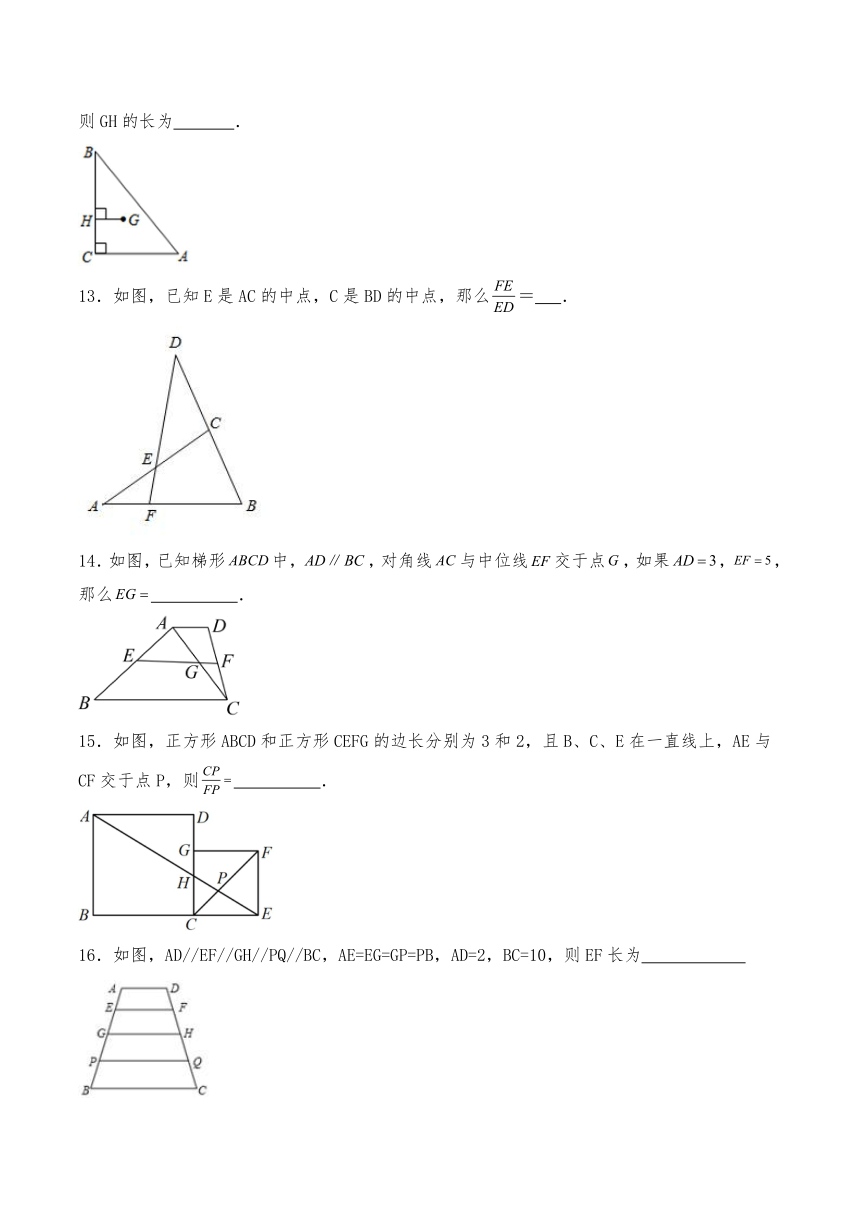
12.如图,在Rt△ABC中,∠ACB=90°,AC=6,点G是△ABC的重心,GH⊥BC,垂足是H,则GH的长为 .
13.如图,已知E是AC的中点,C是BD的中点,那么= .
14.如图,已知梯形中,,对角线与中位线交于点,如果,,那么 .
15.如图,正方形ABCD和正方形CEFG的边长分别为3和2,且B、C、E在一直线上,AE与CF交于点P,则 .
16.如图,AD//EF//GH//PQ//BC,AE=EG=GP=PB,AD=2,BC=10,则EF长为
17.如图,△ABC的中线AD、BE相交于点G,过点G作交BC于点H,如果,那么 .
18.如图,点是反比例函数上的点,过作轴,连接交于点,若,且的面积为5,则的值为 .
19.新定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做等高底三角形,这条边叫做等底.如图,△ABC是等高底三角形,是等底,点关于直线的对称点是点,连接,如果点是的重心,那么的值是 .
20.折纸游戏:小明剪出一个直角三角形的纸片,其中,,,找出的中点,在上找任意一点,以为对称轴折叠,得到,点的对应点为点,小明发现,当点的位置不同时,与△ABC的三边位置关系也不同,请帮小明解决问题:当时,的长为 .
三、解答题
21.如图,点是△ABC的重心.
(1)________;
(2)若,求长.
22.如图,G为△ABC的重心,,求的值.
23.如图,已知,它们依次交直线、、于点A、B、C和点D、E、F和点Q、H、P,与相交于的中点G,若.
(1)如果,求的长;
(2)在(1)的条件下,如果,求的长.
24.如图,在中,对角线和相交于点,,,.
(1)求证:是菱形;
(2)延长至点,连接交于点,若.求的值.
25.如图,已知四边形是菱形,点E是对角线上的一点,连接并延长交于点F,交的延长线于点G,连接.
(1)求证:;
(2)求证:.
26.阅读材料:
角平分线分线段成比例定理:如图1,在△ABC中,平分,则.
下面是这个定理的部分证明过程:
证明:如图2,过点C作,交的延长线于点E.……
解决问题:
(1)请按照上面的证明思路,写出该证明的剩余过程;
(2)如图3,在△ABC中,是角平分线,,,,求的长.
27.如图1,在△ABC中,截线交于点,交于点,交的延长线于点.
(1)求证:;
(2)若截线经过△ABC的重心点,如图2,利用(1)中的结论,求证:.
28.如图1,在△ABC中,,点D在上,点E在上,,延长到F,使得,过点F作,交的延长线于点G.
(1)求证:;
(2)如图2,当点D与点B重合,且,求证:点B为的重心.
29.在△ABC中,,,点为直线上一个动点(点不与点,重合),连接,将线段绕点逆时针旋转得线段,连接,
(1)如图1,若点在线段上,
①依题意补全图1;
②用等式表示线段,,之间的数量关系,并证明
(2)若点在线段的延长线上,且,设,,直接写出的长(用含,的式子表示);
答案
一、单选题
1.C
【分析】本题考查了重心到顶点的距离与重心到对边中点的距离之比为,熟记重心的性质是解题的关键.根据重心性质可得,从而可得答案.
【解析】解:∵是边上的中线,点是重心,
∴,
∵,
∴,
故选:C.
2.A
【分析】根据重心可得,结合可得,即可得到答案;
【解析】解:∵P是△ABC重心,
∴,
∵,
∴,
∴,
故选A.
3.D
【分析】根据平行线分线段成比例的性质,即可解答.
【解析】
,
,
故选:D.
4.A
【分析】抓住已知条件:GE∥BD, GF∥AC,利用平行线分线段成比例以及中间比代换,对各选项一一判断即可求解.
【解析】∵GE∥BD,∴
∵GF∥AC,∴
∴,A选项正确;
∵GE∥BD,∴
∵GF∥AC,∴
∴,B选项错误;
∵GE∥BD,∴
∵GF∥AC,∴
∴,C选项错误;
∵GE∥BD,∴,D选项错误;
故选:A
5.A
【分析】作交于,根据是中点可得,根据平行线分线段成比例可得,有已知条件可得,进而可得.
【解析】解:作交于,
是的中线,
,
,
,
,
,
,
,
.
故选A.
6.C
【分析】利用相似三角形的判定和性质以及平行线分线段成比例定理证明即可;
【解析】∵DE∥CF,
∴△DEK∽△CFK,
∴,
∵EK∥AD,
∴,
∴,
故选C.
7.D
【分析】根据三角形的重心性质可判断选项A、B;根据等边三角形的性质得到,可判断选项C;根据三角形的中线将三角形的面积平分可判断选项D.
【解析】解:A、∵△ABC的中线相交于点G,
∴点G为△ABC的重心,故选项A正确,不符合题意;
B、∵点G 为△ABC的重心,
∴,即,故选项B正确,不符合题意;
C、∵△ABC为等边三角形,
∴,
∵,,
∴,,
∴,故选项C正确,不符合题意;
D、∵,
∴,则,
∴,故选项D错误,符合题意,
故选:D.
8.D
【分析】利用平行四边形的性质以及平行线分线段成比例定理解决问题即可.
【解析】解:∵四边形是平行四边形,
∴,,,,
∴故A正确,不符合题意;
∵,
∴,
又∵.
∴,故B正确,不符合题意;
∴,
∴,,
∴,故C正确,不符合题意;
∵与不一定相等,不一定等于, 而,故D错误,符合题意;
故选:D.
9.C
【分析】本题主要考查了折叠的性质,平行线分线段成比例定理,过点M作于D,由折叠的性质可得,则,,证明,再证明,得到,即可得到.
【解析】解:如图所示,过点M作于D,
由折叠的性质可得,
∵,
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
故选:C.
10.D
【分析】本题考查的是平行线,全等三角形.熟练掌握平行线分线段成比例,全等三角形的判定与性质,是解决问题的关键.
先根据平行线性质和中点性质证明,再证明,从而可得答案.
【解析】如图,设与的交点为G,
∵点M是的中点,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∵
∴,
∴,
∴.
故选:D.
二、填空题
11.
【分析】本题考查了重心的定义与性质,结合勾股定理,直角三角形斜边中线的性质,关键是掌握重心性质并运用勾股定理列式求解是解题关键.本题先利用重心求出和,再利用勾股定理列式整体法求出,最后利用直角三角形斜边中线性质和重心性质求出.
【解析】解:如图,设延长线交于点,延长线交于点,延长线交于点,
∵点是重心,,,
∴,,
∵,
∴,,
∴,
①+②得:,
化简得:,
∴,
∴,
∵点是重心,,
∴,
∴,
故答案为:.
12.2
【分析】如图,连接AG并延长AG交BC于D,由重心的性质可知,可得,由GH⊥BC,∠ACB=90°可得GH//BC,根据平行线分线段成比例定理即可得答案.
【解析】如图,连接AG并延长AG交BC于D,
∵点G是△ABC的重心,
∴AG=2GD,即,
∴,
∵由GH⊥BC,∠ACB=90°,
∴GH//BC,
∴,
∵AC=6,
∴GH=AC·=6×=2,
故答案为:2
13.
【分析】过点C作,交DF于点G,根据平行线分线段成比例定理可得,,由此即可求得答案.
【解析】解:如图,过点C作,交DF于点G,
∵,E是AC的中点,
∴,
∴,
∴,
∵,C是BD的中点,
∴,
∴,
∴,
∴,
故答案为:.
14.
【分析】根据梯形中位线的性质得到,因为,,则,在根据平行线分线段成比例得到是的中点,从而利用三角形中位线的性质即可得到即可确定答案.
【解析】解:梯形中,,梯形的中位线为,
,,
,,
,
,是的中点,
由平行线分线段成比例得到,
,
为△ABC的中位线,即,
故答案为:.
15.
【分析】由CH∥AB,推出,即,再由CH∥EF,推出,即可求解.
【解析】∵正方形ABCD和正方形CEFG的边长分别为3和2,且B、C、E在一直线上,
∴EF=CE=2,AB=BC=3,BE=2+3=5,CH∥EF,CH∥AB,
由CH∥AB,
∴,即,
∴CH=,
由CH∥EF,
∴,
故答案为:.
16.4
【分析】过点D作AB的平行线,把线段分在所得的平行四边形和三角形两部分中,利用平行线所夹线段成比例的性质可以求解.
【解析】解:过点D作DM∥AB,交BC于点M,交EF、GH、PQ分别于点N、K、O,
∵AD∥BC,AB∥DM,
∴ABMD为平行四边形,
又AD∥EF∥GH∥PQ∥BC,
同理得到四边形AEND、AGKD、APOD都为平行四边形,
∴AD=BM=EN=PO=2,
∴CM=8,
∵EF∥BC, AE=EG=GP=PB,
∴,
∴NF=2,
∴EF=EN+NF=4,
故答案为4.
17.6
【分析】根据三角形重心的性质和平行线分线段成比例解答即可.
【解析】解:的中线AD、BE相交于点G,
,
,
,
,
故答案为6
18.20
【分析】本题考查反比例函数的性质,数形结合思想以及运算求解能力,过点A作轴于点E,设,分析可知,结合的面积为5,可得,进而得解.
【解析】解:如图,过点A作轴于点E,
∵轴,轴,
∴,
∵,
∴,则,
∵点A是反比例函数上的点,
∴设,
∴,则,
将代入得:,
解得:,
∴,
∵的面积为5,
∴,整理得,,
解得.
故答案为:20.
19.
【分析】延长与交于点,根据轴对称性质得,,,再由是等高底三角形,是等底,得,再根据三角形的重心定理得,设,则,由勾股定理用表示,进而计算的值便可.
【解析】解:延长与交于点,如图所示:
点A关于直线的对称点是点,
,,,
是等高底三角形,是等底,
,
点是的重心,
,
设,则,
,
故答案为:.
20.或
【分析】分情况讨论,于没有交点时和于有交点时,根据含角的直角三角形的性质,结合平行线分线段成比例,即可求解.
【解析】解:是直角三角形,,,
,,
①如图,当时,设的延长线交于点,则,
,
,
由翻折的性质可知,,,
,
又点是的中点,
,
,即,
;
②如图,当时,设交于点,则,
同理可得,,
,
,即,
;
综上所述,的长为或.
故答案为:或.
三、解答题
21.(1)解:∵点为△ABC的重心(即:点为△ABC三条中线、、的交点),
∴,则,
故答案为:;
(2)∵点为△ABC的重心,
∴由三角形中线性质可得:,,,
则:,,
∴,,
∴,
则,即:,
∵,
∴,
22.解: 点为△ABC的重心,
,
∴
,
,
点为的重心,
点是边的中点,
;
点为△ABC的重心,
,
,
,
∴.
23.(1)∵,
∴,
∴,
∴ ,
∴;
(2)∵点G是的中点,,
∴,
∴,
∵
∴
∴
∴
24.(1)证明:四边形是平行四边形,,,
,,
,
,
是直角三角形,且,
,
是菱形;
(2)解:如图,过点作,交于点,
则,
,
由(1)可知,是菱形,
,,
,
,,
,
,
,
,
.
25.(1)证明:由菱形可得,,,
∵,
∴,
∴,
∵,
∴,
∴.
(2)证明:∵,
∴,
∵,
∴,
∴,
即.
26.(1)证明:∵,
∴,,.
∵平分,
∴,
∴,
∴,
∴.
(2)解:∵是角平分线,
∴.
∵,,,
∴,解得,经检验符合题意.
故的长为.
27.(1)证明:过点C作交于点G,如图,
∴,,
∴.
(2)证明:如图,连接并延长交于点,
由截可得,则,
由截可得,则;
∵点是△ABC的重心,
∴为边上的中线,且,
∴.
28.(1)证明:∵,
∴,
∵,
∴,
∵,
∴,
∴,
在△ABC和中,
,
∴,
∴;
(2)证明:在和中,
,
∴,
∴,
当点D与点B重合时,
∵,,
∴,
由(1)知,即,
∴平分,
∵,
∴,
∴边的中线与边的中线交于点,
∴点B为的重心.
29.(1)解:①如图所示,
②,
证明:如图所示,过点作交于点,
∵在△ABC中,,,
∴,则是等腰直角三角形,
∴,
∵将线段绕点逆时针旋转得线段,则,
∴,,
∴
∴
∴
即
(2)解:如图所示,过点作交的延长线于点,
∵在△ABC中,,,
∴,则是等腰直角三角形,
∴,
∵将线段绕点逆时针旋转得线段,则,
∴,,
∴,
∴,
∵,
∴
∴
∴
∴,
∴,
在中,,,
∴.
一、单选题
1.如图,在△ABC中,是边上的中线,是重心.如果,那么线段的长为( )
A.1 B.2 C.3 D.6
2.如图,P是△ABC重心,且经过点P,则的值为( )
A. B. C. D.
3.如图,在△ABC中,,,下列结论正确的是( )
A. B. C. D.
4.如图,在△ABC中,点D在边BC上,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A.; B.; C.; D..
5.如图,是△ABC的中线,E是上一点,,的延长线交于F,则的值为( )
A. B. C. D.
6.如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F,连接CD,交EF于点K,则下列说法正确的是( )
A. B.
C. D.
7.如图,在△ABC中,中线相交于点G,下列说法错误的是( )
A.点G为△ABC的重心 B.
C.当△ABC为等边三角形时, D.
8.如图,平行四边形中,连接,在的延长线上取一点,点为的中点,连接,交、分别为点、点,则下列结论错误的是( ).
A. B.
C. D.
9.如图,在中,,点M在边上,线段沿着过M的直线折叠,点C恰巧落在边上的点N处.如果,,那么a与b满足的关系式是( )
A. B. C. D.
10.如图,点D,E,F分别在△ABC的边上,,,,点M是的中点,连接并延长交于点N,的值是( )
A. B. C. D.
二、填空题
11.在中,,点是重心,如果,,那么 .
12.如图,在Rt△ABC中,∠ACB=90°,AC=6,点G是△ABC的重心,GH⊥BC,垂足是H,则GH的长为 .
13.如图,已知E是AC的中点,C是BD的中点,那么= .
14.如图,已知梯形中,,对角线与中位线交于点,如果,,那么 .
15.如图,正方形ABCD和正方形CEFG的边长分别为3和2,且B、C、E在一直线上,AE与CF交于点P,则 .
16.如图,AD//EF//GH//PQ//BC,AE=EG=GP=PB,AD=2,BC=10,则EF长为
17.如图,△ABC的中线AD、BE相交于点G,过点G作交BC于点H,如果,那么 .
18.如图,点是反比例函数上的点,过作轴,连接交于点,若,且的面积为5,则的值为 .
19.新定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做等高底三角形,这条边叫做等底.如图,△ABC是等高底三角形,是等底,点关于直线的对称点是点,连接,如果点是的重心,那么的值是 .
20.折纸游戏:小明剪出一个直角三角形的纸片,其中,,,找出的中点,在上找任意一点,以为对称轴折叠,得到,点的对应点为点,小明发现,当点的位置不同时,与△ABC的三边位置关系也不同,请帮小明解决问题:当时,的长为 .
三、解答题
21.如图,点是△ABC的重心.
(1)________;
(2)若,求长.
22.如图,G为△ABC的重心,,求的值.
23.如图,已知,它们依次交直线、、于点A、B、C和点D、E、F和点Q、H、P,与相交于的中点G,若.
(1)如果,求的长;
(2)在(1)的条件下,如果,求的长.
24.如图,在中,对角线和相交于点,,,.
(1)求证:是菱形;
(2)延长至点,连接交于点,若.求的值.
25.如图,已知四边形是菱形,点E是对角线上的一点,连接并延长交于点F,交的延长线于点G,连接.
(1)求证:;
(2)求证:.
26.阅读材料:
角平分线分线段成比例定理:如图1,在△ABC中,平分,则.
下面是这个定理的部分证明过程:
证明:如图2,过点C作,交的延长线于点E.……
解决问题:
(1)请按照上面的证明思路,写出该证明的剩余过程;
(2)如图3,在△ABC中,是角平分线,,,,求的长.
27.如图1,在△ABC中,截线交于点,交于点,交的延长线于点.
(1)求证:;
(2)若截线经过△ABC的重心点,如图2,利用(1)中的结论,求证:.
28.如图1,在△ABC中,,点D在上,点E在上,,延长到F,使得,过点F作,交的延长线于点G.
(1)求证:;
(2)如图2,当点D与点B重合,且,求证:点B为的重心.
29.在△ABC中,,,点为直线上一个动点(点不与点,重合),连接,将线段绕点逆时针旋转得线段,连接,
(1)如图1,若点在线段上,
①依题意补全图1;
②用等式表示线段,,之间的数量关系,并证明
(2)若点在线段的延长线上,且,设,,直接写出的长(用含,的式子表示);
答案
一、单选题
1.C
【分析】本题考查了重心到顶点的距离与重心到对边中点的距离之比为,熟记重心的性质是解题的关键.根据重心性质可得,从而可得答案.
【解析】解:∵是边上的中线,点是重心,
∴,
∵,
∴,
故选:C.
2.A
【分析】根据重心可得,结合可得,即可得到答案;
【解析】解:∵P是△ABC重心,
∴,
∵,
∴,
∴,
故选A.
3.D
【分析】根据平行线分线段成比例的性质,即可解答.
【解析】
,
,
故选:D.
4.A
【分析】抓住已知条件:GE∥BD, GF∥AC,利用平行线分线段成比例以及中间比代换,对各选项一一判断即可求解.
【解析】∵GE∥BD,∴
∵GF∥AC,∴
∴,A选项正确;
∵GE∥BD,∴
∵GF∥AC,∴
∴,B选项错误;
∵GE∥BD,∴
∵GF∥AC,∴
∴,C选项错误;
∵GE∥BD,∴,D选项错误;
故选:A
5.A
【分析】作交于,根据是中点可得,根据平行线分线段成比例可得,有已知条件可得,进而可得.
【解析】解:作交于,
是的中线,
,
,
,
,
,
,
,
.
故选A.
6.C
【分析】利用相似三角形的判定和性质以及平行线分线段成比例定理证明即可;
【解析】∵DE∥CF,
∴△DEK∽△CFK,
∴,
∵EK∥AD,
∴,
∴,
故选C.
7.D
【分析】根据三角形的重心性质可判断选项A、B;根据等边三角形的性质得到,可判断选项C;根据三角形的中线将三角形的面积平分可判断选项D.
【解析】解:A、∵△ABC的中线相交于点G,
∴点G为△ABC的重心,故选项A正确,不符合题意;
B、∵点G 为△ABC的重心,
∴,即,故选项B正确,不符合题意;
C、∵△ABC为等边三角形,
∴,
∵,,
∴,,
∴,故选项C正确,不符合题意;
D、∵,
∴,则,
∴,故选项D错误,符合题意,
故选:D.
8.D
【分析】利用平行四边形的性质以及平行线分线段成比例定理解决问题即可.
【解析】解:∵四边形是平行四边形,
∴,,,,
∴故A正确,不符合题意;
∵,
∴,
又∵.
∴,故B正确,不符合题意;
∴,
∴,,
∴,故C正确,不符合题意;
∵与不一定相等,不一定等于, 而,故D错误,符合题意;
故选:D.
9.C
【分析】本题主要考查了折叠的性质,平行线分线段成比例定理,过点M作于D,由折叠的性质可得,则,,证明,再证明,得到,即可得到.
【解析】解:如图所示,过点M作于D,
由折叠的性质可得,
∵,
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
故选:C.
10.D
【分析】本题考查的是平行线,全等三角形.熟练掌握平行线分线段成比例,全等三角形的判定与性质,是解决问题的关键.
先根据平行线性质和中点性质证明,再证明,从而可得答案.
【解析】如图,设与的交点为G,
∵点M是的中点,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∵
∴,
∴,
∴.
故选:D.
二、填空题
11.
【分析】本题考查了重心的定义与性质,结合勾股定理,直角三角形斜边中线的性质,关键是掌握重心性质并运用勾股定理列式求解是解题关键.本题先利用重心求出和,再利用勾股定理列式整体法求出,最后利用直角三角形斜边中线性质和重心性质求出.
【解析】解:如图,设延长线交于点,延长线交于点,延长线交于点,
∵点是重心,,,
∴,,
∵,
∴,,
∴,
①+②得:,
化简得:,
∴,
∴,
∵点是重心,,
∴,
∴,
故答案为:.
12.2
【分析】如图,连接AG并延长AG交BC于D,由重心的性质可知,可得,由GH⊥BC,∠ACB=90°可得GH//BC,根据平行线分线段成比例定理即可得答案.
【解析】如图,连接AG并延长AG交BC于D,
∵点G是△ABC的重心,
∴AG=2GD,即,
∴,
∵由GH⊥BC,∠ACB=90°,
∴GH//BC,
∴,
∵AC=6,
∴GH=AC·=6×=2,
故答案为:2
13.
【分析】过点C作,交DF于点G,根据平行线分线段成比例定理可得,,由此即可求得答案.
【解析】解:如图,过点C作,交DF于点G,
∵,E是AC的中点,
∴,
∴,
∴,
∵,C是BD的中点,
∴,
∴,
∴,
∴,
故答案为:.
14.
【分析】根据梯形中位线的性质得到,因为,,则,在根据平行线分线段成比例得到是的中点,从而利用三角形中位线的性质即可得到即可确定答案.
【解析】解:梯形中,,梯形的中位线为,
,,
,,
,
,是的中点,
由平行线分线段成比例得到,
,
为△ABC的中位线,即,
故答案为:.
15.
【分析】由CH∥AB,推出,即,再由CH∥EF,推出,即可求解.
【解析】∵正方形ABCD和正方形CEFG的边长分别为3和2,且B、C、E在一直线上,
∴EF=CE=2,AB=BC=3,BE=2+3=5,CH∥EF,CH∥AB,
由CH∥AB,
∴,即,
∴CH=,
由CH∥EF,
∴,
故答案为:.
16.4
【分析】过点D作AB的平行线,把线段分在所得的平行四边形和三角形两部分中,利用平行线所夹线段成比例的性质可以求解.
【解析】解:过点D作DM∥AB,交BC于点M,交EF、GH、PQ分别于点N、K、O,
∵AD∥BC,AB∥DM,
∴ABMD为平行四边形,
又AD∥EF∥GH∥PQ∥BC,
同理得到四边形AEND、AGKD、APOD都为平行四边形,
∴AD=BM=EN=PO=2,
∴CM=8,
∵EF∥BC, AE=EG=GP=PB,
∴,
∴NF=2,
∴EF=EN+NF=4,
故答案为4.
17.6
【分析】根据三角形重心的性质和平行线分线段成比例解答即可.
【解析】解:的中线AD、BE相交于点G,
,
,
,
,
故答案为6
18.20
【分析】本题考查反比例函数的性质,数形结合思想以及运算求解能力,过点A作轴于点E,设,分析可知,结合的面积为5,可得,进而得解.
【解析】解:如图,过点A作轴于点E,
∵轴,轴,
∴,
∵,
∴,则,
∵点A是反比例函数上的点,
∴设,
∴,则,
将代入得:,
解得:,
∴,
∵的面积为5,
∴,整理得,,
解得.
故答案为:20.
19.
【分析】延长与交于点,根据轴对称性质得,,,再由是等高底三角形,是等底,得,再根据三角形的重心定理得,设,则,由勾股定理用表示,进而计算的值便可.
【解析】解:延长与交于点,如图所示:
点A关于直线的对称点是点,
,,,
是等高底三角形,是等底,
,
点是的重心,
,
设,则,
,
故答案为:.
20.或
【分析】分情况讨论,于没有交点时和于有交点时,根据含角的直角三角形的性质,结合平行线分线段成比例,即可求解.
【解析】解:是直角三角形,,,
,,
①如图,当时,设的延长线交于点,则,
,
,
由翻折的性质可知,,,
,
又点是的中点,
,
,即,
;
②如图,当时,设交于点,则,
同理可得,,
,
,即,
;
综上所述,的长为或.
故答案为:或.
三、解答题
21.(1)解:∵点为△ABC的重心(即:点为△ABC三条中线、、的交点),
∴,则,
故答案为:;
(2)∵点为△ABC的重心,
∴由三角形中线性质可得:,,,
则:,,
∴,,
∴,
则,即:,
∵,
∴,
22.解: 点为△ABC的重心,
,
∴
,
,
点为的重心,
点是边的中点,
;
点为△ABC的重心,
,
,
,
∴.
23.(1)∵,
∴,
∴,
∴ ,
∴;
(2)∵点G是的中点,,
∴,
∴,
∵
∴
∴
∴
24.(1)证明:四边形是平行四边形,,,
,,
,
,
是直角三角形,且,
,
是菱形;
(2)解:如图,过点作,交于点,
则,
,
由(1)可知,是菱形,
,,
,
,,
,
,
,
,
.
25.(1)证明:由菱形可得,,,
∵,
∴,
∴,
∵,
∴,
∴.
(2)证明:∵,
∴,
∵,
∴,
∴,
即.
26.(1)证明:∵,
∴,,.
∵平分,
∴,
∴,
∴,
∴.
(2)解:∵是角平分线,
∴.
∵,,,
∴,解得,经检验符合题意.
故的长为.
27.(1)证明:过点C作交于点G,如图,
∴,,
∴.
(2)证明:如图,连接并延长交于点,
由截可得,则,
由截可得,则;
∵点是△ABC的重心,
∴为边上的中线,且,
∴.
28.(1)证明:∵,
∴,
∵,
∴,
∵,
∴,
∴,
在△ABC和中,
,
∴,
∴;
(2)证明:在和中,
,
∴,
∴,
当点D与点B重合时,
∵,,
∴,
由(1)知,即,
∴平分,
∵,
∴,
∴边的中线与边的中线交于点,
∴点B为的重心.
29.(1)解:①如图所示,
②,
证明:如图所示,过点作交于点,
∵在△ABC中,,,
∴,则是等腰直角三角形,
∴,
∵将线段绕点逆时针旋转得线段,则,
∴,,
∴
∴
∴
即
(2)解:如图所示,过点作交的延长线于点,
∵在△ABC中,,,
∴,则是等腰直角三角形,
∴,
∵将线段绕点逆时针旋转得线段,则,
∴,,
∴,
∴,
∵,
∴
∴
∴
∴,
∴,
在中,,,
∴.
