沪教版七年级数学下册 17.4全等三角形的判定(ASA和AAS)(含解析)
文档属性
| 名称 | 沪教版七年级数学下册 17.4全等三角形的判定(ASA和AAS)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-17 10:03:15 | ||
图片预览


文档简介
17.4全等三角形的判定(ASA和AAS)
一、单选题
1.如图所示,,在下列选项中选择一个其他条件,其中不能使的选项是( )
A. B. C. D.
2.如图,点,,在同一直线上,若,,则下列选项中,不能判定的是( )
A. B. C. D.
3.如图,小明不慎将一块三角形的玻璃打碎为三块,他想只带其中一块碎片到商店去配一块与原来一样的三角形玻璃,那么他应该带去的一块是( )
A.① B.② C.③ D.都可以
4.如图,,,若,,则的长是( )
A.5 B.4 C.3 D.5.5
5.已知如图,要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点,使,这时只要出的长,就知道AB的长,那么判定≌的理由是( )
A.ASA B.AAS C.SAS D.HL
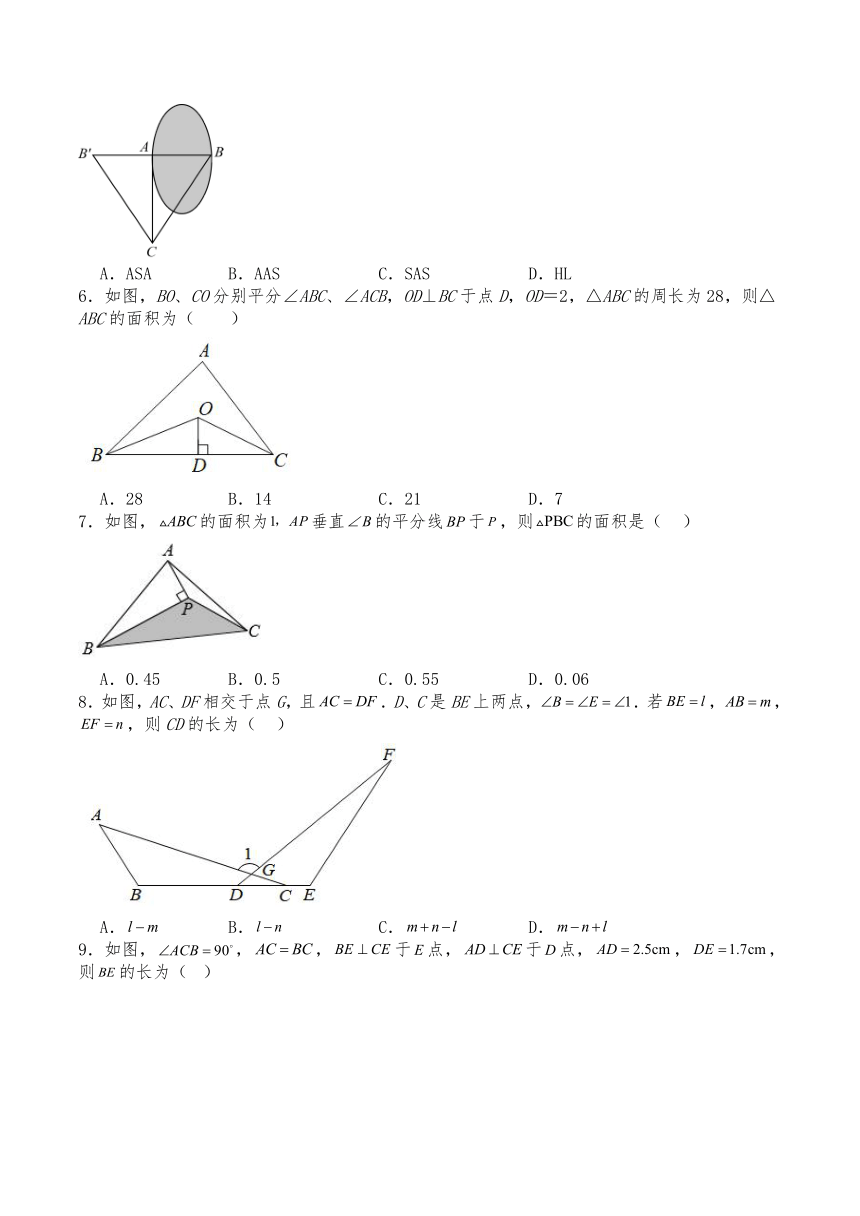
6.如图,BO、CO分别平分∠ABC、∠ACB,OD⊥BC于点D,OD=2,△ABC的周长为28,则△ABC的面积为( )
A.28 B.14 C.21 D.7
7.如图,的面积为垂直的平分线于,则的面积是( )
A.0.45 B.0.5 C.0.55 D.0.06
8.如图,AC、DF相交于点G,且.D、C是BE上两点,.若,,,则CD的长为( )
A. B. C. D.
9.如图,,,于点,于点,,,则的长为( )
A. B. C. D.
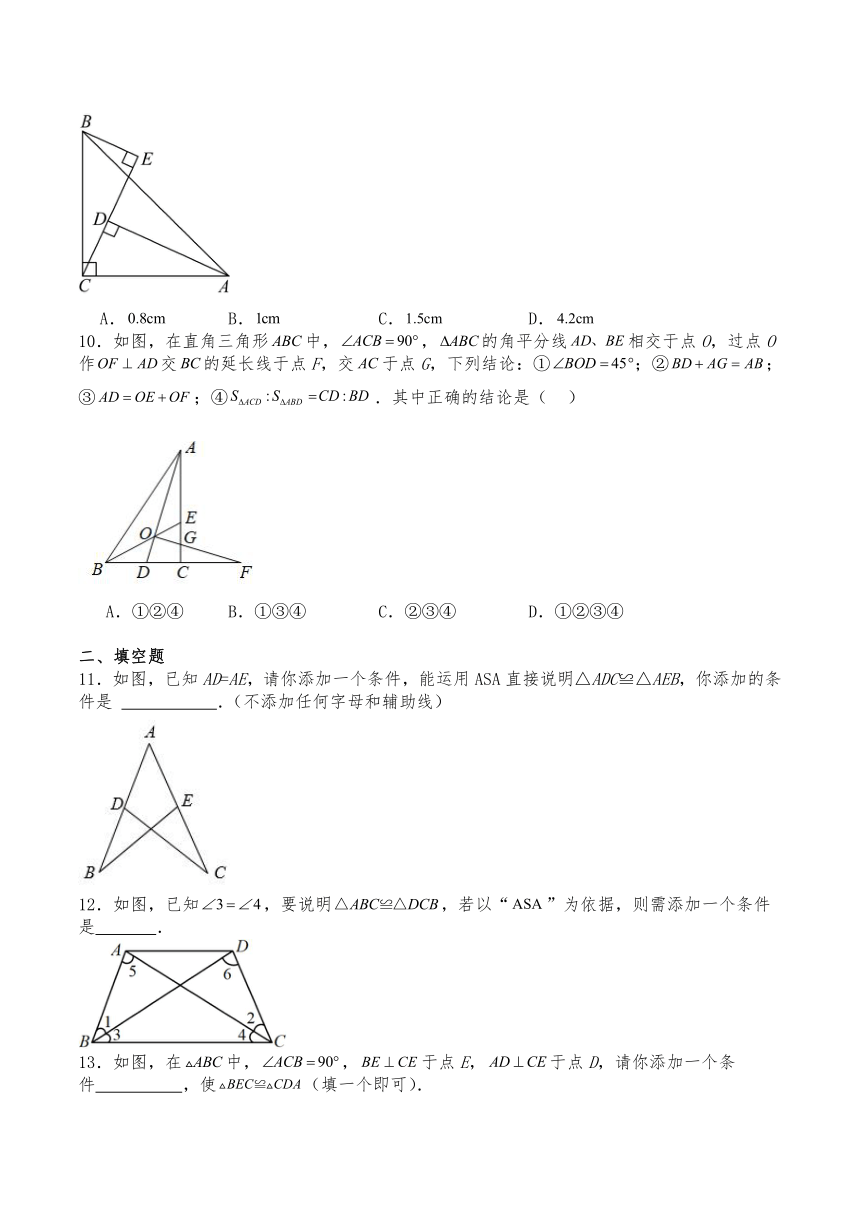
10.如图,在直角三角形中,,的角平分线相交于点O,过点O作交的延长线于点F,交于点G,下列结论:①;②;③;④.其中正确的结论是( )
A.①②④ B.①③④ C.②③④ D.①②③④
二、填空题
11.如图,已知AD=AE,请你添加一个条件,能运用ASA直接说明△ADC≌△AEB,你添加的条件是 .(不添加任何字母和辅助线)
12.如图,已知,要说明,若以“”为依据,则需添加一个条件是 .
13.如图,在中,,于点E,于点D,请你添加一个条件 ,使(填一个即可).
14.如图,在中,,,,,平分交于D,于E,则的周长等于 .
15.如图,在中,是边上的高,是边上的高,且交于点F.若,则线段的长度为 .
16.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF
∥EB;③∠FAN=∠EAM;④△ACN≌△ABM其中正确的有 .
17.如图,中,,,分别过点、作过点的直线的垂线、,垂足分别为、,若,,则 .
18.如图,在中,平分交于点D,若,,则 .
三、解答题
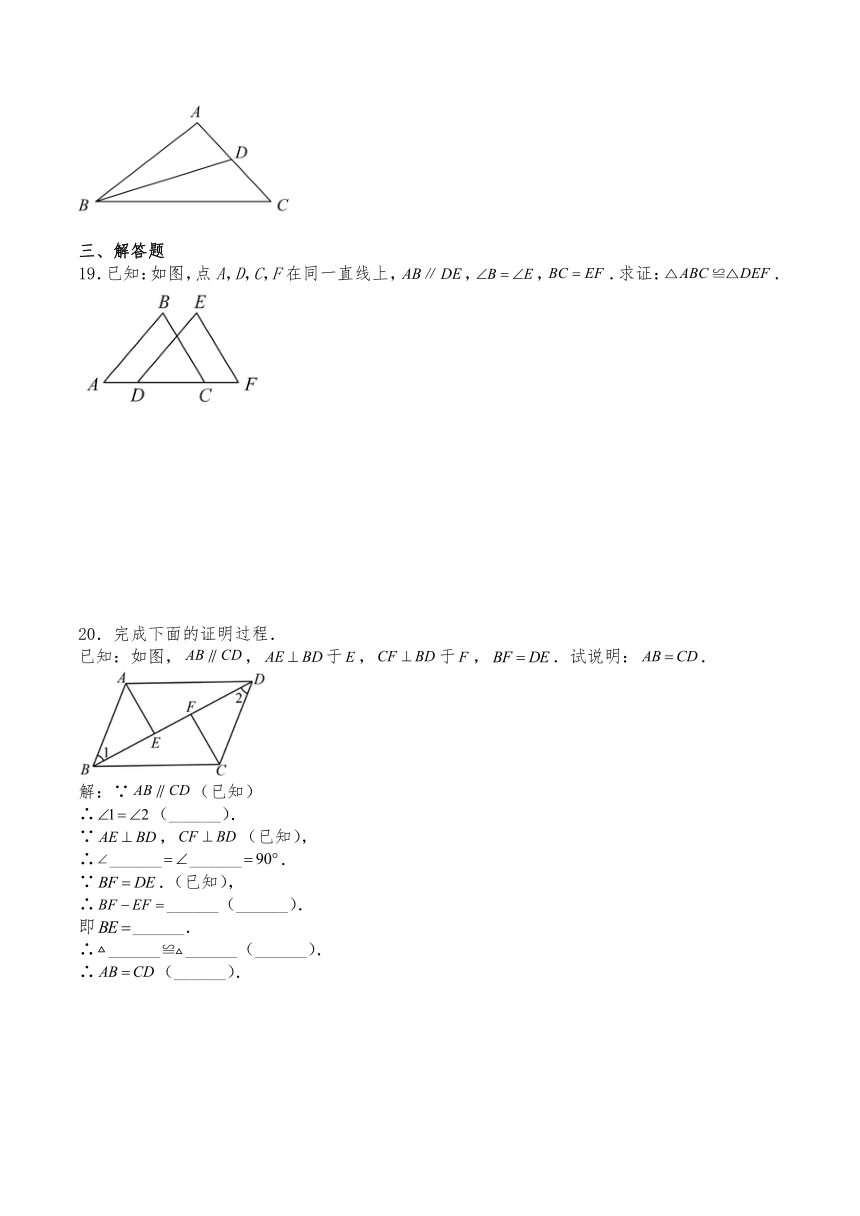
19.已知:如图,点A,D,C,F在同一直线上,,,.求证:.
20.完成下面的证明过程.
已知:如图,,于,于,.试说明:.
解:∵(已知)
∴(______).
∵,(已知),
∴____________.
∵.(已知),
∴______(______).
即______.
∴____________(______).
∴(______).
21.如图,已知点是线段上一点,,.
(1)求证:;
(2)求证:.
22.已知:如图,点B,F,C,E在一条直线上,,,且.求证:.
23.如图,,点D在边上,,和相交于点O.求证:.
24.如图,中,是边上的中线,过C作,垂足为F,过B作交的延长线于D.
(1)求证:;
(2)若,求的长.
25.如图,点B,C分别在射线,上,点E,F都在内部的射线上.已知,且.
(1)求证:△ABE≌△CAF;
(2)试判断,,之间的数量关系,并说明理由.
26.如图,在中,,,于点,于点.求证:
(1);
(2).
27.如图①,在中,,,过点C在外作直线,于点M,于点N.
(1)求证:;
(2)如图②,若过点C作直线与线段相交,于点M,于点N(),(1)中的结论是否仍然成立?若不成立,请写出正确的结论,并说明理由.
28.(1)如图1,,求的长度.
(2)如图2,,探索的数量关系,并证明.
(3)如图3,在中,,则______.
答案
一、单选题
1.D
【分析】首先根据可得,,根据,可得,再加上每个选项中的条件进行分析,即可求解.
【解析】解:∵,
∴,,
选项A,,与已知条件形成,能判定成立,不符合题意;
选项B,,与已知条件形成,能判定成立,不符合题意;
选项C,,可得,与已知条件形成,能判定成立,不符合题意;
选项D,,与已知条件形成,不能判定成立,符合题意;
故选:D.
2.A
【分析】根据平行线的性质“两直线平行,同位角相等”可知,然后结合题意和各个选项,由三角形判定条件即可获得答案.
【解析】解:∵,
∴,再结合已知条件可知:
A. 若,不能证明两三角形全等,符合题意;
B. 若,可利用“”证明,故不符合题意;
C. 若,可利用“”证明,故不符合题意;
D. 若,可利用“”证明,故不符合题意.
故选:A.
3.C
【分析】根据全等三角形的判定方法“角边角”可以判定应当带③去.
【解析】解:由图形可知,③有完整的两角与夹边,根据“角边角”可以作出与原三角形全等的三角形,
所以,最省事的做法是带③去.
故选:C.
4.A
【分析】本题考查全等三角形判定及性质.根据题意先证明出,再利用全等性质得,再利用线段间关系即可得到本题答案.
【解析】解:根据题意:
在和中,
,
∴,
∴,
∵,
∴,
故选:A.
5.A
【分析】直接利用全等三角形的判定方法得出答案.
【解析】解:∵AC⊥AB,
∴,
在和中,
,
∴≌,
∴.
故选A.
6.A
【分析】连接OA,过点O作于点E,作于点F,则由角平分线的性质定理得:OE=OF=OD=2,再由即可求得结果.
【解析】解:连接OA,过点O作于点E,作于点F,如图
∵BO平分,,,
在和中,
,
∴,
∴OE=OD=2
同理:OF=OD=2
∴OE=OF=OD=2
∵
=
=28
∴
故选:A.
7.B
【分析】延长交于E,证明,得出,说明,即可得出答案.
【解析】解:延长交于E,
∵垂直的平分线于P,
∴,
又∵,,
∴,
∴,
∴和等底同高,
,
∴.
故选:B.
8.C
【分析】首先根据题意证明出,然后根据全等三角形的性质求解即可.
【解析】解:∵,
∴
∵,
∴
又∵,
∴
∴
∴.
故选:C.
9.A
【分析】根据题意证明,得到BE=DC,CE=AD,故可求出BE的长.
【解析】解:,,
,
.
,
.
在和中,
,
,
,,
,
.
故选A.
10.A
【分析】根据角平分线的定义、三角形外角的性质与直角三角形性质可以判断①是否正确;延长交于H,通过证明,,利用全等的性质来判断②是否正确;通过证明,利用性质判断③是否正确;根据同高的两个三角形的面积比等于它们的底边长之比,直接判断④是否正确;从而得解.
【解析】解:的角平分线相交于点O,
,,
===
故①正确;
延长交于H,如图所示:
,
又,
,
,
,
,
,,
,
故②正确;
,,
,
,
,
,
又,,
,
,
,
故③错误;
同高的两个三角形面积之比等于底边长之比,
,
故④正确;
因此正确的有:①②④;
故选A.
二、填空题
11.∠ADC=∠AEB
【分析】根据全等三角形的判定定理求解即可.
【解析】解:添加条件∠ADC=∠AEB,理由如下:
在中,
,
∴(ASA),
故答案为:∠ADC=∠AEB.
12.
【分析】根据证明,即可.
【解析】解:添加,理由如下:
∵,,,
∴.
故答案为:
13.(答案不唯一)
【分析】两个三角形全等已具备的条件是:,,根据三角形全等的判定方法即可确定添加的条件.
【解析】解:添加的条件是,
,,
,
,
,
,
在和中,
,
.
故答案为:(答案不唯一).
14.
【分析】证明,可得,,求出,根据的周长等于可得答案.
【解析】解:∵平分,,
∴,,
又∵,
∴,
∴,,
∴,
∴的周长为:,
故答案为:.
15.5
【分析】先证明,再根据全等三角形的性质可得,即可算出的长.
【解析】解:∵是边上的高,是边上的高,
∴,
∴,
∴,
在和△BDF中,
∵,
∴,
∴,
∴,
∴,
故答案为:5.
16.①③④
【分析】由∠E=∠F=90°,∠B=∠C,AE=AF,利用“AAS”得到△ABE与△ACF全等,根据全等三角形的对应边相等且对应角相等即可得到∠EAB与∠FAC相等,AE与AF相等,AB与AC相等,然后在等式∠EAB=∠FAC两边都减去∠MAN,得到∠EAM与∠FAN相等,然后再由∠E=∠F=90°,AE=AF,∠EAM=∠FAN,利用“ASA”得到△AEM与△AFN全等,利用全等三角形的对应边相等,对应角相等得到选项①和③正确;然后再∠C=∠B,AC=AB,∠CAN=∠BAM,利用“ASA”得到△ACN与△ABM全等,故选项④正确;若选项②正确,得到∠F与∠BDN相等,且都为90°,而∠BDN不一定为90°,故②错误.
【解析】解:在△ABE和△ACF中,
∠E=∠F=90°,AE=AF,∠B=∠C,
∴△ABE≌△ACF,
∴∠EAB=∠FAC,AE=AF,AB=AC,
∴∠EAB -∠MAN=∠FAC -∠NAM,即∠EAM=∠FAN,
在△AEM和△AFN中,
∠E=∠F=90°,AE=AF,∠EAM=∠FAN,
∴△AEM≌△AFN,
∴EM=FN,∠FAN=∠EAM,故选项①和③正确;
在△ACN和△ABM中,
∠C=∠B,AC=AB,∠CAN=∠BAM(公共角),
∴△ACN≌△ABM,故选项④正确;
若AF∥EB,∠F=∠BDN=90°,而∠BDN不一定为90°,故②错误,
则正确的选项有:①③④.
故答案为①③④
17.5
【分析】首先证明,然后再根据定理证明,根据全等三角形的性质可得,,进而得到答案.
【解析】解:,
,
,
,
,
,
,
,
在和中,,
,
,
.
故答案为:5.
18.6
【分析】延长到E,使得,连接,可得,即可得,进而解题即可.
【解析】如图,延长到E,使得,连接,
则
又∵
∴
∵平分
∴
∵
∴
∴
∵
∴
解得:
故答案为:6.
三、解答题
19.证明: ,
,
在和中,
,
().
20.证明:(已知)
(两直线平行,内错角相等).
(已知),
.
,(已知),
(等式性质),
即.
,
(全等三角形的对应边相等).
故答案为:两直线平行,内错角相等;;等式性质;;全等三角形的对应边相等.
21.(1)证明:,
,
,
在和中,
,
;
(2)解:,
,,
,
.
22.解:
,
,
在和中,
(ASA).
23.证明:∵,
即,
而,
∴,
∵,
∴.
24.(1)∵,
∴.
∴.
在和中,
∵
∴.
∴.
(2)∵,
∴,
∵是边上的中线,
∴,且.
∴.
25.(1)证明:∵,,
∴,
同理:,
在和中,
∴.
(2)解:,理由如下:
∵△ABE≌△CAF,
∴,,
∵,
∴.
26.(1)证明: 于点,于点,,
,
,
在和中,
.
(2)解:由(1)知,,
,,
∵DE=CE -CD,
,
.
27.(1)证明:于,过作于,
,
,
,
,
∴∠MAC=∠NCB,
在和中,
,
,
,,
;
(2)解:(1)中的结论不成立,与、之间的数量关系为.理由如下:
于,过作于,
,
,
,
,
∴∠MAC=∠NCB,
在和中,
,
,
,,
.
28.(1)解:∵,
∴,
∵,
∴,
在和中,
∴,
∴,
∴;
(2),证明如下:
∵,
∴,
∴∠,
∴,
∴,
∴,
∴;
(3)如图:在△ABC内部作交于F,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
一、单选题
1.如图所示,,在下列选项中选择一个其他条件,其中不能使的选项是( )
A. B. C. D.
2.如图,点,,在同一直线上,若,,则下列选项中,不能判定的是( )
A. B. C. D.
3.如图,小明不慎将一块三角形的玻璃打碎为三块,他想只带其中一块碎片到商店去配一块与原来一样的三角形玻璃,那么他应该带去的一块是( )
A.① B.② C.③ D.都可以
4.如图,,,若,,则的长是( )
A.5 B.4 C.3 D.5.5
5.已知如图,要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点,使,这时只要出的长,就知道AB的长,那么判定≌的理由是( )
A.ASA B.AAS C.SAS D.HL
6.如图,BO、CO分别平分∠ABC、∠ACB,OD⊥BC于点D,OD=2,△ABC的周长为28,则△ABC的面积为( )
A.28 B.14 C.21 D.7
7.如图,的面积为垂直的平分线于,则的面积是( )
A.0.45 B.0.5 C.0.55 D.0.06
8.如图,AC、DF相交于点G,且.D、C是BE上两点,.若,,,则CD的长为( )
A. B. C. D.
9.如图,,,于点,于点,,,则的长为( )
A. B. C. D.
10.如图,在直角三角形中,,的角平分线相交于点O,过点O作交的延长线于点F,交于点G,下列结论:①;②;③;④.其中正确的结论是( )
A.①②④ B.①③④ C.②③④ D.①②③④
二、填空题
11.如图,已知AD=AE,请你添加一个条件,能运用ASA直接说明△ADC≌△AEB,你添加的条件是 .(不添加任何字母和辅助线)
12.如图,已知,要说明,若以“”为依据,则需添加一个条件是 .
13.如图,在中,,于点E,于点D,请你添加一个条件 ,使(填一个即可).
14.如图,在中,,,,,平分交于D,于E,则的周长等于 .
15.如图,在中,是边上的高,是边上的高,且交于点F.若,则线段的长度为 .
16.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF
∥EB;③∠FAN=∠EAM;④△ACN≌△ABM其中正确的有 .
17.如图,中,,,分别过点、作过点的直线的垂线、,垂足分别为、,若,,则 .
18.如图,在中,平分交于点D,若,,则 .
三、解答题
19.已知:如图,点A,D,C,F在同一直线上,,,.求证:.
20.完成下面的证明过程.
已知:如图,,于,于,.试说明:.
解:∵(已知)
∴(______).
∵,(已知),
∴____________.
∵.(已知),
∴______(______).
即______.
∴____________(______).
∴(______).
21.如图,已知点是线段上一点,,.
(1)求证:;
(2)求证:.
22.已知:如图,点B,F,C,E在一条直线上,,,且.求证:.
23.如图,,点D在边上,,和相交于点O.求证:.
24.如图,中,是边上的中线,过C作,垂足为F,过B作交的延长线于D.
(1)求证:;
(2)若,求的长.
25.如图,点B,C分别在射线,上,点E,F都在内部的射线上.已知,且.
(1)求证:△ABE≌△CAF;
(2)试判断,,之间的数量关系,并说明理由.
26.如图,在中,,,于点,于点.求证:
(1);
(2).
27.如图①,在中,,,过点C在外作直线,于点M,于点N.
(1)求证:;
(2)如图②,若过点C作直线与线段相交,于点M,于点N(),(1)中的结论是否仍然成立?若不成立,请写出正确的结论,并说明理由.
28.(1)如图1,,求的长度.
(2)如图2,,探索的数量关系,并证明.
(3)如图3,在中,,则______.
答案
一、单选题
1.D
【分析】首先根据可得,,根据,可得,再加上每个选项中的条件进行分析,即可求解.
【解析】解:∵,
∴,,
选项A,,与已知条件形成,能判定成立,不符合题意;
选项B,,与已知条件形成,能判定成立,不符合题意;
选项C,,可得,与已知条件形成,能判定成立,不符合题意;
选项D,,与已知条件形成,不能判定成立,符合题意;
故选:D.
2.A
【分析】根据平行线的性质“两直线平行,同位角相等”可知,然后结合题意和各个选项,由三角形判定条件即可获得答案.
【解析】解:∵,
∴,再结合已知条件可知:
A. 若,不能证明两三角形全等,符合题意;
B. 若,可利用“”证明,故不符合题意;
C. 若,可利用“”证明,故不符合题意;
D. 若,可利用“”证明,故不符合题意.
故选:A.
3.C
【分析】根据全等三角形的判定方法“角边角”可以判定应当带③去.
【解析】解:由图形可知,③有完整的两角与夹边,根据“角边角”可以作出与原三角形全等的三角形,
所以,最省事的做法是带③去.
故选:C.
4.A
【分析】本题考查全等三角形判定及性质.根据题意先证明出,再利用全等性质得,再利用线段间关系即可得到本题答案.
【解析】解:根据题意:
在和中,
,
∴,
∴,
∵,
∴,
故选:A.
5.A
【分析】直接利用全等三角形的判定方法得出答案.
【解析】解:∵AC⊥AB,
∴,
在和中,
,
∴≌,
∴.
故选A.
6.A
【分析】连接OA,过点O作于点E,作于点F,则由角平分线的性质定理得:OE=OF=OD=2,再由即可求得结果.
【解析】解:连接OA,过点O作于点E,作于点F,如图
∵BO平分,,,
在和中,
,
∴,
∴OE=OD=2
同理:OF=OD=2
∴OE=OF=OD=2
∵
=
=28
∴
故选:A.
7.B
【分析】延长交于E,证明,得出,说明,即可得出答案.
【解析】解:延长交于E,
∵垂直的平分线于P,
∴,
又∵,,
∴,
∴,
∴和等底同高,
,
∴.
故选:B.
8.C
【分析】首先根据题意证明出,然后根据全等三角形的性质求解即可.
【解析】解:∵,
∴
∵,
∴
又∵,
∴
∴
∴.
故选:C.
9.A
【分析】根据题意证明,得到BE=DC,CE=AD,故可求出BE的长.
【解析】解:,,
,
.
,
.
在和中,
,
,
,,
,
.
故选A.
10.A
【分析】根据角平分线的定义、三角形外角的性质与直角三角形性质可以判断①是否正确;延长交于H,通过证明,,利用全等的性质来判断②是否正确;通过证明,利用性质判断③是否正确;根据同高的两个三角形的面积比等于它们的底边长之比,直接判断④是否正确;从而得解.
【解析】解:的角平分线相交于点O,
,,
===
故①正确;
延长交于H,如图所示:
,
又,
,
,
,
,
,,
,
故②正确;
,,
,
,
,
,
又,,
,
,
,
故③错误;
同高的两个三角形面积之比等于底边长之比,
,
故④正确;
因此正确的有:①②④;
故选A.
二、填空题
11.∠ADC=∠AEB
【分析】根据全等三角形的判定定理求解即可.
【解析】解:添加条件∠ADC=∠AEB,理由如下:
在中,
,
∴(ASA),
故答案为:∠ADC=∠AEB.
12.
【分析】根据证明,即可.
【解析】解:添加,理由如下:
∵,,,
∴.
故答案为:
13.(答案不唯一)
【分析】两个三角形全等已具备的条件是:,,根据三角形全等的判定方法即可确定添加的条件.
【解析】解:添加的条件是,
,,
,
,
,
,
在和中,
,
.
故答案为:(答案不唯一).
14.
【分析】证明,可得,,求出,根据的周长等于可得答案.
【解析】解:∵平分,,
∴,,
又∵,
∴,
∴,,
∴,
∴的周长为:,
故答案为:.
15.5
【分析】先证明,再根据全等三角形的性质可得,即可算出的长.
【解析】解:∵是边上的高,是边上的高,
∴,
∴,
∴,
在和△BDF中,
∵,
∴,
∴,
∴,
∴,
故答案为:5.
16.①③④
【分析】由∠E=∠F=90°,∠B=∠C,AE=AF,利用“AAS”得到△ABE与△ACF全等,根据全等三角形的对应边相等且对应角相等即可得到∠EAB与∠FAC相等,AE与AF相等,AB与AC相等,然后在等式∠EAB=∠FAC两边都减去∠MAN,得到∠EAM与∠FAN相等,然后再由∠E=∠F=90°,AE=AF,∠EAM=∠FAN,利用“ASA”得到△AEM与△AFN全等,利用全等三角形的对应边相等,对应角相等得到选项①和③正确;然后再∠C=∠B,AC=AB,∠CAN=∠BAM,利用“ASA”得到△ACN与△ABM全等,故选项④正确;若选项②正确,得到∠F与∠BDN相等,且都为90°,而∠BDN不一定为90°,故②错误.
【解析】解:在△ABE和△ACF中,
∠E=∠F=90°,AE=AF,∠B=∠C,
∴△ABE≌△ACF,
∴∠EAB=∠FAC,AE=AF,AB=AC,
∴∠EAB -∠MAN=∠FAC -∠NAM,即∠EAM=∠FAN,
在△AEM和△AFN中,
∠E=∠F=90°,AE=AF,∠EAM=∠FAN,
∴△AEM≌△AFN,
∴EM=FN,∠FAN=∠EAM,故选项①和③正确;
在△ACN和△ABM中,
∠C=∠B,AC=AB,∠CAN=∠BAM(公共角),
∴△ACN≌△ABM,故选项④正确;
若AF∥EB,∠F=∠BDN=90°,而∠BDN不一定为90°,故②错误,
则正确的选项有:①③④.
故答案为①③④
17.5
【分析】首先证明,然后再根据定理证明,根据全等三角形的性质可得,,进而得到答案.
【解析】解:,
,
,
,
,
,
,
,
在和中,,
,
,
.
故答案为:5.
18.6
【分析】延长到E,使得,连接,可得,即可得,进而解题即可.
【解析】如图,延长到E,使得,连接,
则
又∵
∴
∵平分
∴
∵
∴
∴
∵
∴
解得:
故答案为:6.
三、解答题
19.证明: ,
,
在和中,
,
().
20.证明:(已知)
(两直线平行,内错角相等).
(已知),
.
,(已知),
(等式性质),
即.
,
(全等三角形的对应边相等).
故答案为:两直线平行,内错角相等;;等式性质;;全等三角形的对应边相等.
21.(1)证明:,
,
,
在和中,
,
;
(2)解:,
,,
,
.
22.解:
,
,
在和中,
(ASA).
23.证明:∵,
即,
而,
∴,
∵,
∴.
24.(1)∵,
∴.
∴.
在和中,
∵
∴.
∴.
(2)∵,
∴,
∵是边上的中线,
∴,且.
∴.
25.(1)证明:∵,,
∴,
同理:,
在和中,
∴.
(2)解:,理由如下:
∵△ABE≌△CAF,
∴,,
∵,
∴.
26.(1)证明: 于点,于点,,
,
,
在和中,
.
(2)解:由(1)知,,
,,
∵DE=CE -CD,
,
.
27.(1)证明:于,过作于,
,
,
,
,
∴∠MAC=∠NCB,
在和中,
,
,
,,
;
(2)解:(1)中的结论不成立,与、之间的数量关系为.理由如下:
于,过作于,
,
,
,
,
∴∠MAC=∠NCB,
在和中,
,
,
,,
.
28.(1)解:∵,
∴,
∵,
∴,
在和中,
∴,
∴,
∴;
(2),证明如下:
∵,
∴,
∴∠,
∴,
∴,
∴,
∴;
(3)如图:在△ABC内部作交于F,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
同课章节目录
