1.1 等腰三角形 课件(共26张PPT) 2024-2025学年 北师大版八年级数学下册
文档属性
| 名称 | 1.1 等腰三角形 课件(共26张PPT) 2024-2025学年 北师大版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 670.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-17 14:51:43 | ||
图片预览








文档简介
(共26张PPT)
北师大版版八年级数学下册课件
第一章 三角形的证明
1 等腰三角形
1.(2022新课标)证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
2.(2022新课标)探索并证明等腰三角形的性质定理:等腰三角形的两个底角相等;底边上的高线、中线及顶角平分线重合.
新课导入
D
A
C
B
得到这个△ABC中 AB和AC有什么关系
新课讲解
知识点1 全等三角形
全等三角形的定义是什么?
新课讲解
1.全等三角形的性质:全等三角形的对应边相等、对应角相等.
2.全等三角形的判定方法
(1)三边分别相等的两个三角形全等(简写成“边边边”或“SSS”).
(2)两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).
(3)两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”).
(4)两边及其夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”)
新课讲解
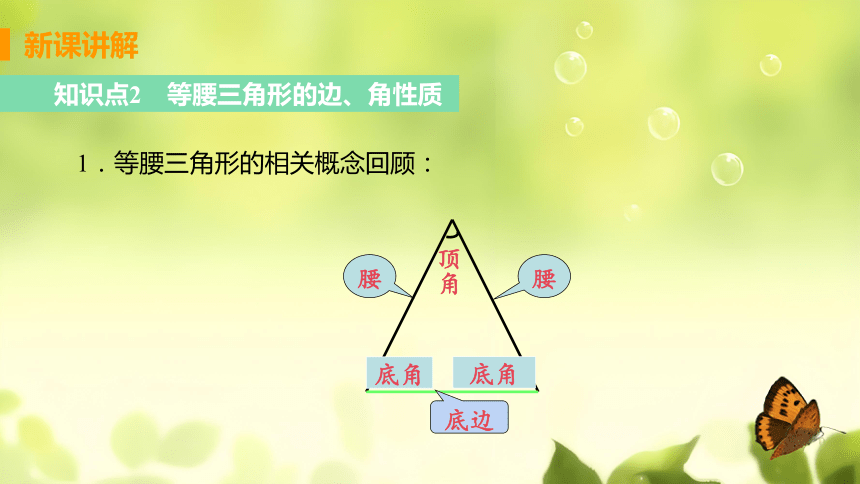
知识点2 等腰三角形的边、角性质
1.等腰三角形的相关概念回顾:
腰
腰
顶角
底角
底角
底边
新课讲解
2.议一议
(1)还记得我们探索过的等腰三角形的性质吗?
(2)请你选择等腰三角形的一条性质进行证明,并与
同伴交流.
新课讲解
定理 等腰三角形的两底角相等.
这一定理可以简述为:等边对等角.
新课讲解
性质:等腰三角形的两底角相等
(简写成“等边对等角”).
新课讲解
知识点3 等腰三角形的“三线合一”性质
在图1 -3中,线段AD还具有怎样的性质?为什么?由
此你能得到什么结论
新课讲解
推论 等腰三角形的顶角平分线、底边上的中线、
底边上的高相互重合(简写成“三线合一”)
课堂小结
1.知识方面:
(1)等腰三角形的性质:等边对等角.
(2)等腰三角形性质的推论:三线合一,即等腰三角
形顶角的平分线、底边上的中线及底边上的高线
互相重合.
2.思想方法:转化思想的应用,等腰三角形的性质是
证明角相等、边相等的重要方法.
(1)全等三角形的判定定理:SSS、 、 、 .
(2)全等三角形的性质定理:全等三角形的对应边 ,对应角 .
全等三角形的判定定理及性质定理(复习)
ASA
SAS
AAS
相等
相等
1.()如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
证明:∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
又∵AB=DE,AC=DF,
∴△ABC≌△DEF(SSS).
∴∠A=∠D.
(1)定理:等腰三角形的两底角 ,简述为“ ”.
(2)如图,在△ABC中,AB=AC.求证:∠B=∠C.
等腰三角形的性质定理
相等
等边对等角
(2)证明:取BC的中点D,连接AD.
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS).∴∠B=∠C.
2.下列各图中,已知AB=AC,写出x的值.
(1)x= (2)x=
(3)x=
70
30
35
推论:等腰三角形顶角的 、底边上的 及底边上的 互相重合(简述为“三线合一”),知一推二.
运用示例:如图,在△ABC中,
∵AB=AC,又∵AD平分∠BAC,
∴DB=DC,AD⊥BC.
等腰三角形性质定理的推论
中线
平分线
高线
3.如图,在△ABC中,AB=AC,AD平分∠BAC,∠BAC=80°,BC=20,则∠BAD= °,∠BDA= °,BD= .
40
90
10
4.【例1】(2024烟台模拟)如图,在△ABC中,点D是边BC上的一点.若AB=AD=DC,∠BAD=44°,则∠C的度数为 .
34°
5.【例2】(2024广州一模)如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,∠BAD=∠CAD.
∵BE⊥AC,∴∠CBE+∠C=∠CAD+∠C=90°.
∴∠CBE=∠CAD.∴∠CBE=∠BAD.
6.【例3】(人教8上P76改编)如图,在△ABC中,AB=AC,点D在线段BC上,AD=BD.
(1)求证:∠BAD=∠C;
(2)若CA=CD,求△ABC三个内角的度数.
(1)证明:∵AB=AC,∴∠B=∠C.
∵AD=BD,∴∠B=∠BAD.∴∠BAD=∠C.
(2)解:∵CA=CD,∴∠CAD=∠CDA,
由(1)得∠B=∠C=∠BAD,
设∠B=x,则∠CDA=∠B+∠BAD=2x,
∴∠CAD=∠CDA=2x,∠BAC=∠CAD+∠BAD=3x,
∴在△ABC中,有∠B+∠C+∠BAC=x+x+3x=180°,
解得x=36°,∴在△ABC中,∠BAC=108°,∠B=∠C=36°.
7.(2024惠东模拟)如图,在等腰三角形ABC中,AB=AC,若以点B为圆心,BC长为半径画弧,交AC于点D,∠A=36°,则∠ADB的度数为( )
A.36° B.60° C.72° D.108°
D
完成本课课后的习题
谢谢大家欣赏
北师大版版八年级数学下册课件
第一章 三角形的证明
1 等腰三角形
1.(2022新课标)证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
2.(2022新课标)探索并证明等腰三角形的性质定理:等腰三角形的两个底角相等;底边上的高线、中线及顶角平分线重合.
新课导入
D
A
C
B
得到这个△ABC中 AB和AC有什么关系
新课讲解
知识点1 全等三角形
全等三角形的定义是什么?
新课讲解
1.全等三角形的性质:全等三角形的对应边相等、对应角相等.
2.全等三角形的判定方法
(1)三边分别相等的两个三角形全等(简写成“边边边”或“SSS”).
(2)两角及其夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).
(3)两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”).
(4)两边及其夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”)
新课讲解
知识点2 等腰三角形的边、角性质
1.等腰三角形的相关概念回顾:
腰
腰
顶角
底角
底角
底边
新课讲解
2.议一议
(1)还记得我们探索过的等腰三角形的性质吗?
(2)请你选择等腰三角形的一条性质进行证明,并与
同伴交流.
新课讲解
定理 等腰三角形的两底角相等.
这一定理可以简述为:等边对等角.
新课讲解
性质:等腰三角形的两底角相等
(简写成“等边对等角”).
新课讲解
知识点3 等腰三角形的“三线合一”性质
在图1 -3中,线段AD还具有怎样的性质?为什么?由
此你能得到什么结论
新课讲解
推论 等腰三角形的顶角平分线、底边上的中线、
底边上的高相互重合(简写成“三线合一”)
课堂小结
1.知识方面:
(1)等腰三角形的性质:等边对等角.
(2)等腰三角形性质的推论:三线合一,即等腰三角
形顶角的平分线、底边上的中线及底边上的高线
互相重合.
2.思想方法:转化思想的应用,等腰三角形的性质是
证明角相等、边相等的重要方法.
(1)全等三角形的判定定理:SSS、 、 、 .
(2)全等三角形的性质定理:全等三角形的对应边 ,对应角 .
全等三角形的判定定理及性质定理(复习)
ASA
SAS
AAS
相等
相等
1.()如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
证明:∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
又∵AB=DE,AC=DF,
∴△ABC≌△DEF(SSS).
∴∠A=∠D.
(1)定理:等腰三角形的两底角 ,简述为“ ”.
(2)如图,在△ABC中,AB=AC.求证:∠B=∠C.
等腰三角形的性质定理
相等
等边对等角
(2)证明:取BC的中点D,连接AD.
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS).∴∠B=∠C.
2.下列各图中,已知AB=AC,写出x的值.
(1)x= (2)x=
(3)x=
70
30
35
推论:等腰三角形顶角的 、底边上的 及底边上的 互相重合(简述为“三线合一”),知一推二.
运用示例:如图,在△ABC中,
∵AB=AC,又∵AD平分∠BAC,
∴DB=DC,AD⊥BC.
等腰三角形性质定理的推论
中线
平分线
高线
3.如图,在△ABC中,AB=AC,AD平分∠BAC,∠BAC=80°,BC=20,则∠BAD= °,∠BDA= °,BD= .
40
90
10
4.【例1】(2024烟台模拟)如图,在△ABC中,点D是边BC上的一点.若AB=AD=DC,∠BAD=44°,则∠C的度数为 .
34°
5.【例2】(2024广州一模)如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,∠BAD=∠CAD.
∵BE⊥AC,∴∠CBE+∠C=∠CAD+∠C=90°.
∴∠CBE=∠CAD.∴∠CBE=∠BAD.
6.【例3】(人教8上P76改编)如图,在△ABC中,AB=AC,点D在线段BC上,AD=BD.
(1)求证:∠BAD=∠C;
(2)若CA=CD,求△ABC三个内角的度数.
(1)证明:∵AB=AC,∴∠B=∠C.
∵AD=BD,∴∠B=∠BAD.∴∠BAD=∠C.
(2)解:∵CA=CD,∴∠CAD=∠CDA,
由(1)得∠B=∠C=∠BAD,
设∠B=x,则∠CDA=∠B+∠BAD=2x,
∴∠CAD=∠CDA=2x,∠BAC=∠CAD+∠BAD=3x,
∴在△ABC中,有∠B+∠C+∠BAC=x+x+3x=180°,
解得x=36°,∴在△ABC中,∠BAC=108°,∠B=∠C=36°.
7.(2024惠东模拟)如图,在等腰三角形ABC中,AB=AC,若以点B为圆心,BC长为半径画弧,交AC于点D,∠A=36°,则∠ADB的度数为( )
A.36° B.60° C.72° D.108°
D
完成本课课后的习题
谢谢大家欣赏
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
