2024-2025学年北师大版八年级数学下册 1.1 课时3 等腰三角形的判定与反证法 课件(共27张PPT)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学下册 1.1 课时3 等腰三角形的判定与反证法 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 704.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-17 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
北师大版八年级数学下册课件
第一章 三角形的证明
1 等腰三角形
课时3 等腰三角形的判定与反证法
1等腰三角形的判定
2反证法.(重点、难点)
3.探索并掌握等腰三角形的判定定理:有两个角相等的三角形是等腰三角形.
4.通过实例体会反证法的含义.
学习目标
新课导入
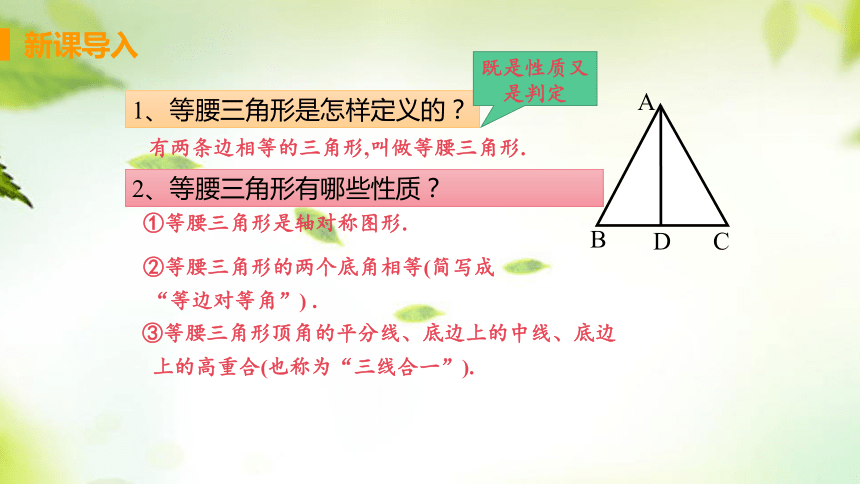
D
A
B
C
1、等腰三角形是怎样定义的?
有两条边相等的三角形,叫做等腰三角形.
①等腰三角形是轴对称图形.
③等腰三角形顶角的平分线、底边上的中线、底边
上的高重合(也称为“三线合一”).
②等腰三角形的两个底角相等(简写成
“等边对等角”) .
2、等腰三角形有哪些性质?
既是性质又是判定
新课讲解
知识点1 等腰三角形的判定
思考
我们知道,如果一个三角形有两条边相等,
那么它们所对的角相等. 反过来,如果一个三角
形有两个角相等,那么它们所对的边有什么关系?
新课讲解
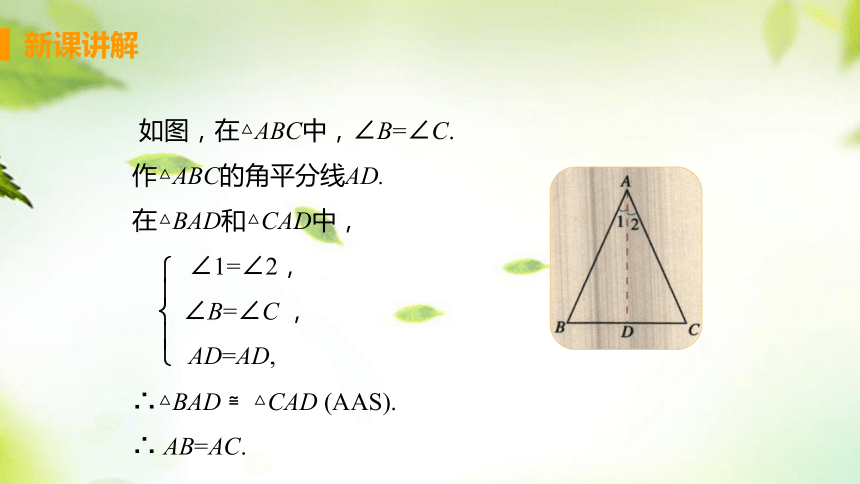
如图,在△ABC中,∠B=∠C.
作△ABC的角平分线AD.
在△BAD和△CAD中,
∠1=∠2,
∠B=∠C ,
AD=AD,
∴△BAD ≌△CAD (AAS).
∴ AB=AC.
新课讲解
1.判定定理:有两个角相等的三角形是等腰三角
形.(简称等角对等边)
应用格式:在△ABC中,∵∠B=∠C, ∴AB=AC.
2.等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.
新课讲解
知识点2 反证法
想一想
小李认为,在一个三角形中,如果两个角不相等,
那么这两个角所对的边也不相等.你认为小明这个结
论成立吗?如果成立,你能证明它吗?
新课讲解
1.定义
在证明时,先假设命题的结论不成立,然后推导出与
定义、基本事实、已有定理或已知条件相矛盾的结果,
从而证明命题的结论一定成立,这种证明方法称为反
证法.
2.利用反证法证明命题的一般步骤
(1)假设命题的结论不成立;
(2)从这个假设出发,经过推理论证,得出矛盾;
(3)由矛盾判定假设不正确,从而肯定命题的结论正确.
新课讲解
3.适宜用反证法证明的命题
反证法主要用于直接证明比较困难的命题,例如
下面几种常见类型的命题就适宜用反证法:
(1)结论以否定形式出现的命题,如钝角三角形中不
能有两个钝角;
(2)唯一性命题,如两条直线相交只有一个交点;
(3)命题的结论以“至多”“至少”等形式叙述的命
题,如一个凸多边形中至多有3个锐角.
课堂小结
1.等腰三角形的判定是把角相等转化为边相等,但前
提是在同一个三角形内.
2.利用反证法解题的一般步骤:
(1)假设;
(2)归谬:从假设出发,经过推理论证得出与已知、定
理、公理等相矛盾的结果;
(3)结论:肯定命题结论正确.
(北师8下P8)我们知道,等腰三角形的两个底角相等.反过来,在一个三角形中,如果有两个角相等,那么它是等腰三角形吗?画画看,你发现了什么?
探索等腰三角形的判定定理
我们可以发现,如果一个三角形中有两个角相等,那么它就是等腰三角形.
1.(北师8下P8、人教8上P77)如图,在△ABC中,∠B=∠C,求证:AB=AC.(提示:添加辅助线,构造全等三角形)
证法一:证明:如图1,作∠BAC的平分线,交BC于点D.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵∠B=∠C,AD=AD,
∴△ABD≌△ACD(AAS).
∴AB=AC.
图1
证法二:证明:如图2,过点A作BC的垂线,垂足为D.
∵AD⊥BC,∴∠ADB=∠ADC=90°.
∵∠B=∠C,AD=AD,
∴△ABD≌△ACD(AAS).
∴AB=AC.
图2
等腰三角形的判定定理
定理 有两个角 的三角形是等腰三角形.
简述为:
几何 语言 如图,在△ABC中,
∵∠B=∠C,
∴
注意 判定等腰三角形的方法有两种:
一种是定义法,另一种是判定定理
等角对等边
相等
AB=AC
2.(北师8下P8、人教8上P92)如图,AB=DC,BD=CA,BD与CA相交于点E.求证:△AED是等腰三角形.
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS).
∴∠ADB=∠DAC.
∴AE=DE.∴△AED是等腰三角形.
反证法
定义 在证明时,先假设命题的 不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.这种证明方法称为反证法
证明 步骤 (1)假设命题的结论不成立;
(2)从这个假设出发,应用正确的推导方法,推导出与定义、基本事实、已有定理或已知条件相矛盾的结果;
(3)由矛盾的结果判定假设不正确,从而肯定命题的结论成立
结论
3.(1)用反证法证明“直角三角形中至少有一个锐角小于或等于45°”时,应先假设( )
A.直角三角形中两个锐角都大于45°
B.直角三角形中两个锐角都不大于45°
C.直角三角形中有一个锐角大于45°
D.直角三角形中有一个锐角不大于45°
(2)用反证法证明“等角对等边”,应先假设
.
A
在一个三角形中,如果有两个角相等,那么这两个角所对的边不相等
4.【例1】(创新题)如图,已知∠AOB,作∠AOB的平分线OC,将直尺DEMN按如图所示的方式摆放,使EM边与OB边重合,顶点D落在OA边上,DN边与OC交于点P.
(1)猜想:△DOP是 三角形;
等腰
(2)补全下面证明过程:
∵OC平分∠AOB,
∴ = .
∵DN∥EM,∴ = .
∴ = .∴ = .
∴△DOP是 三角形.
∠DOP
∠BOP
∠DPO
∠BOP
∠DOP
∠DPO
DO
DP
等腰
7.(2024西安期末)如图,AD平分∠BAC,BD⊥AD,DE∥AC,求证:△BDE是等腰三角形.
证明:∵AD平分∠BAC,∴∠EAD=∠CAD.
∵DE∥AC,
∴∠CAD=∠ADE,∴∠EAD=∠ADE.
∵BD⊥AD,
∴∠ADE+∠BDE=90°,∠EAD+∠B=90°,
∴∠BDE=∠B,∴BE=DE,∴△BDE是等腰三角形.
小结:遇到角平分线+平行线,可构造等腰三角形.
8.(北师8下P9)已知五个正数的和等于1,用反证法证明:这五个正数中至少有一个大于或等于.
证明:假设这五个正数没有一个大于或等于,即都小于,不妨设这五个正数分别为a,b,c,d,e,则a<,b<,c<,d<,e<.
∴a+b+c+d+e<1,这与已知条件a+b+c+d+e=1相矛盾.
∴假设不成立,
∴这五个正数中至少有一个大于或等于.
6.【例3】(北师8下P34改编、人教8上P34)如图,在△ABC中,点D,E分别是AB,AC边上的点,BD=CE,∠ABE=∠ACD,BE与CD相交于点F.求证:△ABC是等腰三角形.
证明:∵∠DFB=∠EFC,∠ABE=∠ACD,BD=CE,
∴△DFB≌△EFC(AAS).∴FB=FC.
∴∠FBC=∠FCB.
∴∠FBC+∠ABE=∠FCB+∠ACD,即∠ABC=∠ACB.
∴AB=AC.∴△ABC是等腰三角形.
请完成本节课后对应习题
布置作业
THANKS
北师大版八年级数学下册课件
第一章 三角形的证明
1 等腰三角形
课时3 等腰三角形的判定与反证法
1等腰三角形的判定
2反证法.(重点、难点)
3.探索并掌握等腰三角形的判定定理:有两个角相等的三角形是等腰三角形.
4.通过实例体会反证法的含义.
学习目标
新课导入
D
A
B
C
1、等腰三角形是怎样定义的?
有两条边相等的三角形,叫做等腰三角形.
①等腰三角形是轴对称图形.
③等腰三角形顶角的平分线、底边上的中线、底边
上的高重合(也称为“三线合一”).
②等腰三角形的两个底角相等(简写成
“等边对等角”) .
2、等腰三角形有哪些性质?
既是性质又是判定
新课讲解
知识点1 等腰三角形的判定
思考
我们知道,如果一个三角形有两条边相等,
那么它们所对的角相等. 反过来,如果一个三角
形有两个角相等,那么它们所对的边有什么关系?
新课讲解
如图,在△ABC中,∠B=∠C.
作△ABC的角平分线AD.
在△BAD和△CAD中,
∠1=∠2,
∠B=∠C ,
AD=AD,
∴△BAD ≌△CAD (AAS).
∴ AB=AC.
新课讲解
1.判定定理:有两个角相等的三角形是等腰三角
形.(简称等角对等边)
应用格式:在△ABC中,∵∠B=∠C, ∴AB=AC.
2.等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.
新课讲解
知识点2 反证法
想一想
小李认为,在一个三角形中,如果两个角不相等,
那么这两个角所对的边也不相等.你认为小明这个结
论成立吗?如果成立,你能证明它吗?
新课讲解
1.定义
在证明时,先假设命题的结论不成立,然后推导出与
定义、基本事实、已有定理或已知条件相矛盾的结果,
从而证明命题的结论一定成立,这种证明方法称为反
证法.
2.利用反证法证明命题的一般步骤
(1)假设命题的结论不成立;
(2)从这个假设出发,经过推理论证,得出矛盾;
(3)由矛盾判定假设不正确,从而肯定命题的结论正确.
新课讲解
3.适宜用反证法证明的命题
反证法主要用于直接证明比较困难的命题,例如
下面几种常见类型的命题就适宜用反证法:
(1)结论以否定形式出现的命题,如钝角三角形中不
能有两个钝角;
(2)唯一性命题,如两条直线相交只有一个交点;
(3)命题的结论以“至多”“至少”等形式叙述的命
题,如一个凸多边形中至多有3个锐角.
课堂小结
1.等腰三角形的判定是把角相等转化为边相等,但前
提是在同一个三角形内.
2.利用反证法解题的一般步骤:
(1)假设;
(2)归谬:从假设出发,经过推理论证得出与已知、定
理、公理等相矛盾的结果;
(3)结论:肯定命题结论正确.
(北师8下P8)我们知道,等腰三角形的两个底角相等.反过来,在一个三角形中,如果有两个角相等,那么它是等腰三角形吗?画画看,你发现了什么?
探索等腰三角形的判定定理
我们可以发现,如果一个三角形中有两个角相等,那么它就是等腰三角形.
1.(北师8下P8、人教8上P77)如图,在△ABC中,∠B=∠C,求证:AB=AC.(提示:添加辅助线,构造全等三角形)
证法一:证明:如图1,作∠BAC的平分线,交BC于点D.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵∠B=∠C,AD=AD,
∴△ABD≌△ACD(AAS).
∴AB=AC.
图1
证法二:证明:如图2,过点A作BC的垂线,垂足为D.
∵AD⊥BC,∴∠ADB=∠ADC=90°.
∵∠B=∠C,AD=AD,
∴△ABD≌△ACD(AAS).
∴AB=AC.
图2
等腰三角形的判定定理
定理 有两个角 的三角形是等腰三角形.
简述为:
几何 语言 如图,在△ABC中,
∵∠B=∠C,
∴
注意 判定等腰三角形的方法有两种:
一种是定义法,另一种是判定定理
等角对等边
相等
AB=AC
2.(北师8下P8、人教8上P92)如图,AB=DC,BD=CA,BD与CA相交于点E.求证:△AED是等腰三角形.
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS).
∴∠ADB=∠DAC.
∴AE=DE.∴△AED是等腰三角形.
反证法
定义 在证明时,先假设命题的 不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.这种证明方法称为反证法
证明 步骤 (1)假设命题的结论不成立;
(2)从这个假设出发,应用正确的推导方法,推导出与定义、基本事实、已有定理或已知条件相矛盾的结果;
(3)由矛盾的结果判定假设不正确,从而肯定命题的结论成立
结论
3.(1)用反证法证明“直角三角形中至少有一个锐角小于或等于45°”时,应先假设( )
A.直角三角形中两个锐角都大于45°
B.直角三角形中两个锐角都不大于45°
C.直角三角形中有一个锐角大于45°
D.直角三角形中有一个锐角不大于45°
(2)用反证法证明“等角对等边”,应先假设
.
A
在一个三角形中,如果有两个角相等,那么这两个角所对的边不相等
4.【例1】(创新题)如图,已知∠AOB,作∠AOB的平分线OC,将直尺DEMN按如图所示的方式摆放,使EM边与OB边重合,顶点D落在OA边上,DN边与OC交于点P.
(1)猜想:△DOP是 三角形;
等腰
(2)补全下面证明过程:
∵OC平分∠AOB,
∴ = .
∵DN∥EM,∴ = .
∴ = .∴ = .
∴△DOP是 三角形.
∠DOP
∠BOP
∠DPO
∠BOP
∠DOP
∠DPO
DO
DP
等腰
7.(2024西安期末)如图,AD平分∠BAC,BD⊥AD,DE∥AC,求证:△BDE是等腰三角形.
证明:∵AD平分∠BAC,∴∠EAD=∠CAD.
∵DE∥AC,
∴∠CAD=∠ADE,∴∠EAD=∠ADE.
∵BD⊥AD,
∴∠ADE+∠BDE=90°,∠EAD+∠B=90°,
∴∠BDE=∠B,∴BE=DE,∴△BDE是等腰三角形.
小结:遇到角平分线+平行线,可构造等腰三角形.
8.(北师8下P9)已知五个正数的和等于1,用反证法证明:这五个正数中至少有一个大于或等于.
证明:假设这五个正数没有一个大于或等于,即都小于,不妨设这五个正数分别为a,b,c,d,e,则a<,b<,c<,d<,e<.
∴a+b+c+d+e<1,这与已知条件a+b+c+d+e=1相矛盾.
∴假设不成立,
∴这五个正数中至少有一个大于或等于.
6.【例3】(北师8下P34改编、人教8上P34)如图,在△ABC中,点D,E分别是AB,AC边上的点,BD=CE,∠ABE=∠ACD,BE与CD相交于点F.求证:△ABC是等腰三角形.
证明:∵∠DFB=∠EFC,∠ABE=∠ACD,BD=CE,
∴△DFB≌△EFC(AAS).∴FB=FC.
∴∠FBC=∠FCB.
∴∠FBC+∠ABE=∠FCB+∠ACD,即∠ABC=∠ACB.
∴AB=AC.∴△ABC是等腰三角形.
请完成本节课后对应习题
布置作业
THANKS
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
