2016届初三数学云南省学业水平考试研讨会 (共91张PPT)
文档属性
| 名称 | 2016届初三数学云南省学业水平考试研讨会 (共91张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-02 13:08:09 | ||
图片预览









文档简介
课件91张PPT。2016年云南省学业水平考试研讨会吴建平 云南师范大学实验中学高级教师数学一、浅谈2016年云南省初中学业水平标准与考试说明与上一年的变化
1.考试能力要求的变化。
2.具体内容与考试要求细目列表的变化。
3.样题的变化。
4.题型示例的变化。
?二、我校初三年级数学备课总复习工作计划 1.分三轮进行总复习,时间按4∶2∶1比例进行。
2.加强培优,辅差工作。
3.学校每月一考,备课组半月一考,班级每周一考。
4.加强集体备课,分块由每个老师准备相关内容。
?
初三数学复习计划交流a、统一思想认识,调整好心态: 1、使所学知识系统化、结构化,将初中三年的数学知识连成一个有机整体,利于学生理解,掌握和灵活运用;2、精讲多练,巩固基本技能,提高运算能力;3、抓好方法教学,引导学生归纳、总结解题的方法与技巧,提高解题能力; 4、做好综合题训练,提高学生综合运用知识分析问题的能力 ;b、集体备课,明确复习思路: 复习策略是两条腿走路: 一是选一本有知识点、又有2016年中考真题的资料进行第一轮分块复习,做到每个知识点都测试批改,要求学生过关 ;二是每周一套中考模拟题测试复习。 c、制定复习目标,激发学生积极参与: 制定班级目标、帮学生正确定位找准目标; 口号:每天进步一点 ;誓言:我们不比基础比进步,不比聪明比刻苦,不比昨天比今天; 理念:不抛弃、不放弃每一个学困生 。 d、制定复习措施: 1、认真钻研教材,根据课标及考纲,明确复习重点;要认真研究云南省初中学业水平标准与考试说明;2、从易到难复习让学生看到希望。 e、细节是重点,基础是关键。
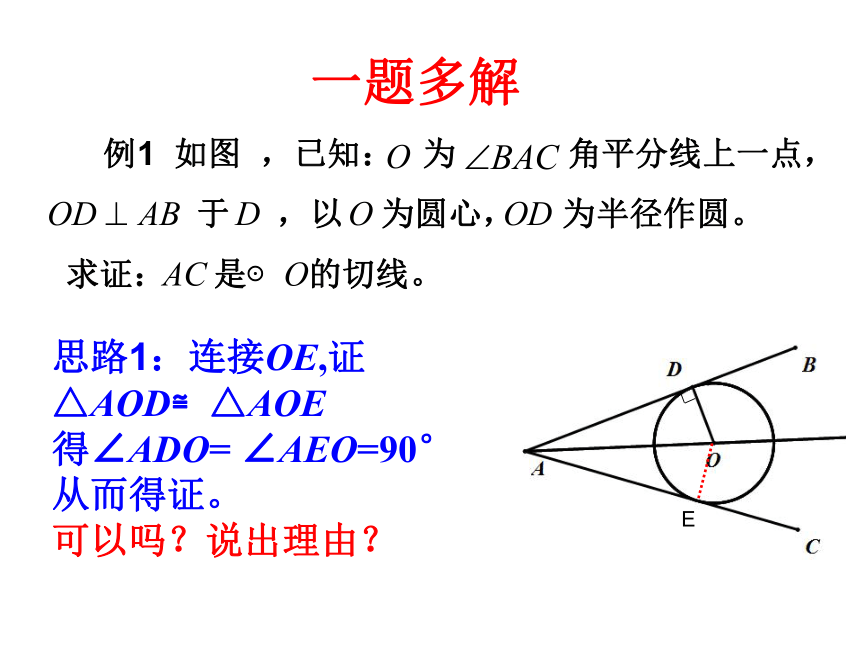
1、在复习中要梳理知识:在梳理过程中,回归教材,挖掘教材中的例题、习题,通过一题多解,一题多变的变式训练增强学生训练的兴趣; 例1 如图 ,已知: 为 角平分线上一点,
于 ,以 为圆心, 为半径作圆。
求证: 是⊙ 的切线。思路1:连接OE,证△AOD≌△AOE
得∠ADO= ∠AEO=90°从而得证。
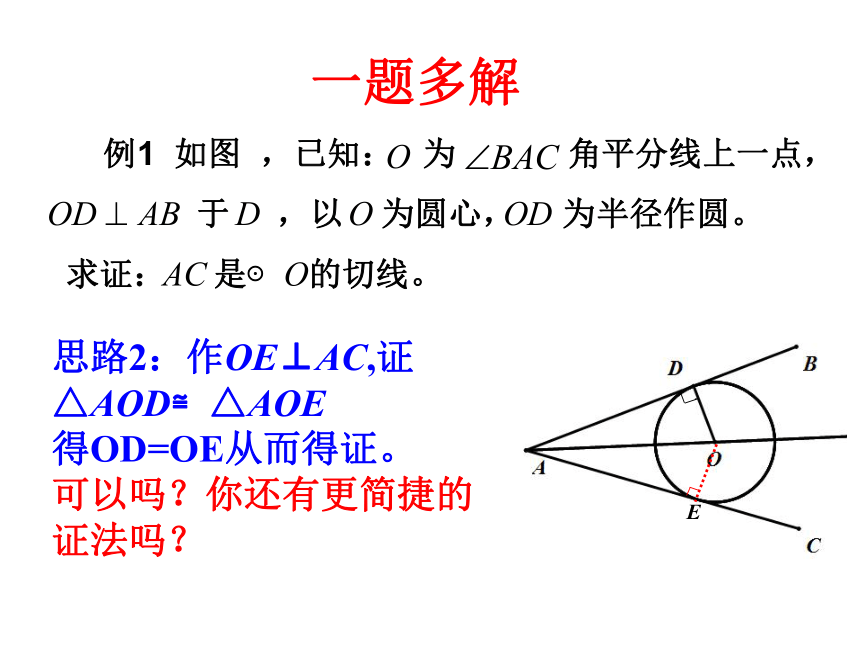
可以吗?说出理由?一题多解 例1 如图 ,已知: 为 角平分线上一点,
于 ,以 为圆心, 为半径作圆。
求证: 是⊙ 的切线。思路2:作OE⊥AC,证△AOD≌△AOE
得OD=OE从而得证。
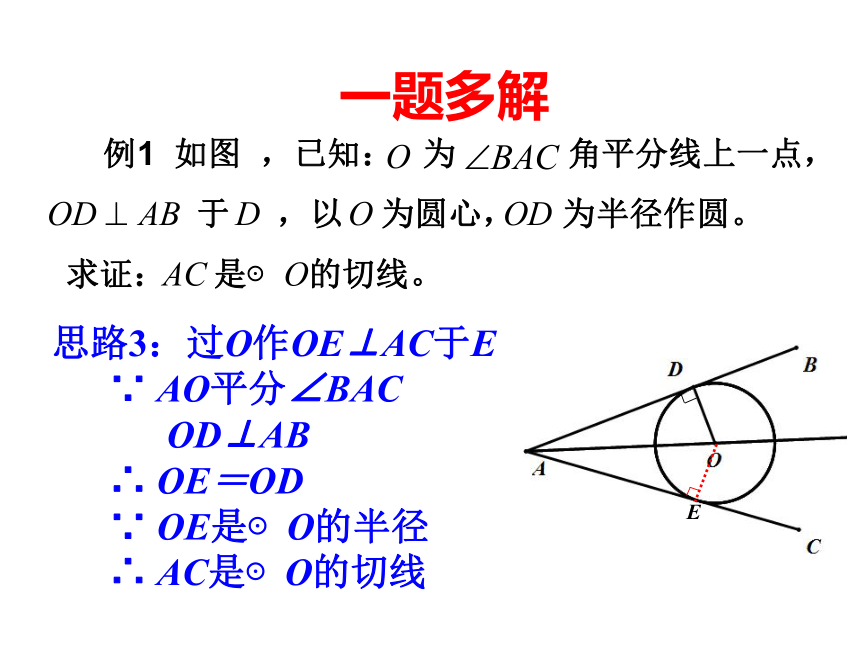
可以吗?你还有更简捷的证法吗?一题多解 例1 如图 ,已知: 为 角平分线上一点,
于 ,以 为圆心, 为半径作圆。
求证: 是⊙ 的切线。一题多解思路3:过O作OE⊥AC于E
∵ AO平分∠BAC
OD⊥AB
∴ OE=OD
∵ OE是⊙O的半径
∴ AC是⊙O的切线
练习2 如图,AB是⊙O 的直径,⊙O交BC的中点于D,
DE⊥AC.
求证:DE与⊙O相切.一题多解变式训练变式1 昆明)如图,已知AB是⊙O的直径,过点E的直线EF与AB的延长线交于点F,AC⊥EF,垂足为C,AE平分∠FAC。
求证:CF是⊙O的切线。(5分)变式2 (广州) 如图,∠C=90o,BD平分∠ABC,DE⊥BD ,设⊙O是△BDE的外接圆。
求证:AC是⊙O的切线。DE⊥BD ,设⊙O是△BDE的外接圆变式训练e、细节是重点,基础是关键。
2、在复习中要注重查缺补漏:要求学生准备一本错题本,把每次测试的错题抄下来改正,便于复习,避免下次犯同样的错误,我们老师也应该准备一本错题本,便于出每日一练题,抓知识点过关; e、细节是重点,基础是关键。
3、抓数学“双基”,要求“会”就要做“对”;e、细节是重点,基础是关键。
4、教会学生从自己的实际情况出发,算分复习,寻找得分点、寻找突破点;5、解题时要培养学生:
①先想后算,审清题目,避免盲目;
②多想少算,理清思路,少走弯路;
③反思巧算,解法优化,过程完整不丢分;
④难度题不说我不会,要说我会多少,分步得分,养成有问必答的习惯; e、细节是重点,基础是关键。
6、过记忆关时可用顺口溜:如:完全平方公式可记为:首加末的完全平方等于首方加末方,首末积的2倍放中央;负指数幂可记为底倒指正;方差可记为偏差的平方的平均数;特殊角300、450、600的三角函数值可记为正弦、余弦的分母都是2,正切的分母都是3,它们的分子分别是根号下1、2、3,3、2、1、,3、9、27;f、摆脱题海归纳出解题规律。1.要想让学生从题海中解脱出来,我们老师就得进入题海去精选有代表性的题目; 2.做题要关注思路、方法、技巧,要注重发现题与题之间的内在联系。要通过比较,发现规律,做到触类旁通,做一题会一类; 3.复习方法要多样化,但每个知识点进行测试批分一定可以激起学生的复习兴趣; g、规范答题格式:1、抓书写;2、抓答题格式:从左至右、从上到下、写出关键理由; 17.(昆明)(6分)如图,点B、D、C、F在一条直线上,且BC = FD,AB = EF.
(1)请你只添加一个条件(不再加辅助线),使△ABC≌△EFD,你添
加的条件是 ;
(2)添加了条件后,证明△ABC≌△EFD.AC=DE……1分……2分……3分……4分……5分中考要求列表法求概率如下(规范格式):中考要求树形图求概率如下(规范格式):g、规范答题格式:3、抓有问必答:特别强调统计题中的有问必答; 4、每个题型都让学生了解评分标准,让学生按评分标准规范答题,平时批试卷时要给过程分。(1)证明:连接OE……………1分
∵AE平分∠FAC
∴∠CAE=∠OAE
又∵OA=OE,
∴ ∠OEA=∠OAE …………..…2分
∴ ∠CAE=∠OEA
∴OE∥AC…………………....…3分
∴∠OEF=∠ACF
又∵AC⊥EF
∴∠OEF=∠ACF=90°
∴OE⊥CF …………………...…4分
又∵点E在⊙O上
∴CF是⊙O的切线…………..…5分
(昆明24题)看看你能得几分?h、复习中要抓好培优辅差工作:对优等生的要求是:
1.课堂上跟老师走;负责帮助一名后进生;看错题本,避免犯同样的错误;
2.每天做一题压轴题,注重把握解题方法、解题思路;切忌死钻偏题、怪题;
3.每周完成一套中考模拟题,提高应试能力;
4.参加年级统一组织的培优辅导。h、复习中要抓好培优辅差工作:对学困生的要求是:
1.课堂跟老师走,寻找自己的强项;
2.组织师徒结对,不懂的随时问师傅问老师;看得分本,寻找得分点,突破点,按自己的目标分可以算分复习;
3.每周完成一套中考模拟题,提高应试能力。基础题分分必争,难度题分步得分,要舍得放弃;
4.参加年级组织的基础过关辅导;三、如何有实效的帮助学生提高数学成绩1.不同时期的教与学。
2.想尽一切办法调动学生学习积极性。
3.掌握好共性与个性的问题处理。
4.有条件实现一对一进行个性问题的分析讲解,有重点分小组实现水平升级。四、2016年考试方向预测和对考生的几点复习与应试的建议 1.全面夯实教学基础知识,构建完善的知识体系。
2.科学确定复习目标,合理安排复习时间和复习内容。
3.精选例体,及时总结解题的经验教训。
4.注意实际应用问题,强调操作实践。
5.注意开放探究,形成数学能力。
?
五、教学反思与教学建议 1.认真落实初中数学基础知识,基本运算教学。
2.从初一开始就重视每一堂课的教学。
3.重视、加强几何的教学。
4.重视对应用问题的教学。
5.要养成书写有条理、工整、整洁的良好学习习惯。
6.加强对数学学习较困难的学生帮助和指导
7.在复习工作中重视教材。
统计与概率部分的复习策略
一、明确依据和方向
二、对比分析 挖掘本质
三、中考复习策略和方法
统计与概率部分的复习策略夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。一、明确依据和方向二、对比分析 挖掘本质三、中考复习策略和方法夯实四基,对比研究,明确方向,刻苦拼搏。一、明确依据和方向 夯实四基,对比研究,明确方向,刻苦拼搏。 我省中考试题是以《云南省学业水平标准与考试说明》为依据来命制的,因此,我们必须认真研读《考试说明》,准确理解和把握考试要求,从而更加高效地进行我们的复习备考工作.1.统计与概率领域的课标要求1.1 内容标准: “统计与概率”主要研究现实生活中的数据和客观世界中的随机现象,它通过对数据收集、整理、描述和分析以及对事件发生可能性的刻画,来帮助人们作出合理的推断和预测.夯实四基,对比研究,明确方向,刻苦拼搏。1.2 总体要求:学生将体会抽样的必要性以及用样本估计总体的思想,进一步学习描述数据的方法,进一步体会概率的意义,能计算简单事件发生的概率. 夯实四基,对比研究,明确方向,刻苦拼搏。1.3 教学要求:
①应注重所学内容与日常生活、自然、社会和科学技术领域的联系,使学生体会统计与概率对制定决策的重要作用;
②应注重使学生从事数据处理的全过程,根据统计结果作出合理的判断;
③应注重使学生在具体情境中体会概率的意义;
④应加强统计与概率之间的联系;
⑤应避免将这部分内容的学习变成数字运算的练习,对有关术语不要求进行严格表述. 夯实四基,对比研究,明确方向,刻苦拼搏。2.统计与概率领域的《中考说明》要求夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。二、对比分析 挖掘本质夯实四基,对比研究,明确方向,刻苦拼搏。云南中考13—15年有关统计试题的比较分析夯实四基,对比研究,明确方向,刻苦拼搏。18.(7分)(2013?云南)近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图.
(1)求出本次被调查的学生数;
(2)请求出统计表中a的值;
(3)求各组人数的众数;
(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.
考点:扇形统计图;用样本估计总体;统计表;众数.
分析:(1)根据A组有12人,占被调查总数的10%,据 此即可求得总人数;
(2)总人数减去其它各组的人数即可求得;
(3)根据众数的定义即可求解;
(4)利用2400乘以对应的比例即可求解.
夯实四基,对比研究,明确方向,刻苦拼搏。5.(3分)(2013?昆明)为了了解2013年昆明市
九年级学生学业水平考试的数学成绩,
从中随机抽取了1000名学生的数学成绩.
下列说法正确的是( ) 本题考查了总体、个体、样本、样本容量的知识,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
点评18.(5分)(2013?昆明)2013年6月6日第一届南亚博览会在昆明举行.某校对七年级学生开展了“南博会知多少?”的调查活动,采取随机抽样的方法进行问卷调查,问卷调查的结果分为“不太了解”、“基本了解”、“比较了解”、“非常了解”四个等级,对调查结果进行统计后,绘制了如下不完整的条形统计图:
根据以上统计图提供的信息,回答下列问题:(1)若“基本了解”的人数占抽样调查人数的25%,此次调查抽取了 学生;
(2)补全条形统计图;
(3)若该校七年级有600名学生,请估计“比较了解”和“非常了解”的学生共有多少人?考点:条形统计图;用样本估计总体.专题:计算题.分析:(1)由“基本了解”的人数除以所占的百分比即可得到调查的学生数;(2)根据学生总数求出“比较了解”的学生数,补全条形统计图即可;(3)求出“比较了解”和“非常了解”的学生在样本中所占的百分比,乘以600即可得到结果.8.(3分)(2014年云南省)学校为了丰富学生课余活动开展了一次“爱我云南,唱我云南”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
成绩(分) 9.40 9.50 9.60 9.70 9.80 9.90
人数 2 3 5 4 3 1
则入围同学决赛成绩的中位数和众数分别是( )
A. 9.70,9.60 B. 9.60,9.60
C.9.60,9.70 D. 9.65,9.60考点: 众数;中位数.
分析: 根据中位数和众数的概念求解.
解答: 解:∵共有18名同学,
则中位数为第9名和第10名同学成绩的平均分,即中位数为:=9.60,
众数为:9.60.
故选B.点评: 本题考查了中位数和众数的概念,一组数据中出现次数最多的数据叫做众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.18.(9分)(2014年云南省)为了解本校九年级学生期末数学考试情况,销量在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?考点: 条形统计图;用样本估计总体;扇形统计图.
分析: (1)抽查人数可由C等所占的比例为50%,根据总数=某等人数÷比例来计算;
(2)可由总数减去A、C、D的人数求得B等的人数,再补全条形统计图;
(3)用样本估计总体.用总人数1200乘以样本中测试成绩等级在80分(含80分)以上的学生所占百分比即可.解答: 解:(1)20÷50%=40(人),
答:这次随机抽取的学生共有40人;
(2)B等级人数:40﹣5﹣20﹣4=1(人)
条形统计图如下:
(3)1200××100%=480(人),
答:这次九年级学生期末数学考试成绩为优秀的学生人数大约有480人.点评: 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.7.(2015云南省)为加快新农村试点示范建设,我省开展了“美丽乡村”的评选活动,下表是我省六个州(市)推荐候选的“美丽乡村”个数统计结果:
在下表统计的数据中,平均数和中位数分别( )
A.42,43.5 B. 42,42 C.31,42 D.36,54夯实四基,对比研究,明确方向,刻苦拼搏。云南中考13—15年有关概率试题的比较分析19.(6分)(2013?昆明)有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线上y= 上的概率.
考点:列表法与树状图法;反比例函数图象上点的坐标特征.专题:图表型.分析:(1)画出树状图即可得解;(2)根据反比例函数图象上点的坐标特征判断出在双曲线上y= 上的情况数,然后根据概率公式列式计算即可得解.解答:解:(1)根据题意画出树状图如下:;(2)一共有9种等可能的情况:(-1,-1),(-1,1),(-1,2),(1,1),(1,-1),(1,2),(2,2),(2,-1),(2,1),点(x,y)落在双曲线上y= 上的有2种情况:(1,2),(2,1)所以,P= 19.(7分)(2014年云南省)某市“艺术节”期间,小明、小亮都想去观看茶艺表演,但是只有一张茶艺表演门票,他们决定采用抽卡片的办法确定谁去.规则如下:
将正面分别标有数字1、2、3、4的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上,随机抽出一张记下数字后放回;重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字.如果两个数字之和为奇数,则小明去;如果两个数字之和为偶数,则小亮去.
(1)请用列表或画树状图的方法表示抽出的两张卡片上的数字之和的所有可能出现的结果;
(2)你认为这个规则公平吗?请说明理由.考点: 游戏公平性;列表法与树状图法.
分析: (1)用列表法将所有等可能的结果一一列举出来即可;
(2)求得两人获胜的概率,若相等则公平,否则不公平.
解答: 解:(1)根据题意列表得:
1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8(2)由列表得:共16种情况,其中奇数有8种,偶数有8种,
∴和为偶数和和为奇数的概率均为0.5,
∴这个游戏公平.
点评: 本题考查了游戏公平性及列表与列树形图的知识,难度不大,是经常出现的一个知识点.20.(2015云南省)现有一个六面分别标有数字1,2,3,4,5,6且质地均匀的正方体骰子,另有三张正面分别标有数字1,2,3的卡片(卡片除数字外,其它都相同).先由小明投骰子一次,记下骰子向上一面出现的数字,然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张,记下卡片上的数字.
(1)请用列表或画树形图(树状图)的方法,求出骰子向上一面出现的数字与卡片上的数字之积为6的概率;
(2)小明和小王做游戏,约定游戏规则如下:若骰子向上一面出现的数字与卡片上的数字之积大于7,则小明赢;若骰子向上一面出现的数字与卡片上的数字之积小于7,则小王赢.问小明和小王谁赢的可能性更大?请说明理由.夯实四基,对比研究,明确方向,刻苦拼搏。三、中考复习策略与方法夯实四基,对比研究,明确方向,刻苦拼搏。全面撒网——形成知识体系夯实四基,对比研究,明确方向,刻苦拼搏。 可以预测:2016年对于统计的考查和前几年的变化不会很大,依然会以一小一大的形式出现,大题8分小题4分,备考时要关注:统计量的计算、从统计图中获取信息,再进行处理信息,从而解决问题. 复习时,要把重点放在:统计概念的理解上,学生读图识图及从图中获取数据信息、进而处理信息的能力的培养上.把各种统计图表相结合让学生读取,读取时注意表(图)头,图中所涉及的量及各种信息,如:各数据之间的关系等.逐步培养统计观念,提高信息处理能力 夯实四基,对比研究,明确方向,刻苦拼搏。2.
概
率夯实四基,对比研究,明确方向,刻苦拼搏。古典概型的概率计算——重点运用列举法(包括列表、画树状图)计算简单事件发生的概率涉及频率估计概率和几何概型的概率计算 理解频率与概率的关系,通过几何图形的面积求概率夯实四基,对比研究,明确方向,刻苦拼搏。 可以预测:2016年的概率试题依然会以8分的解答题出现,备考时,依然要关注:借助列举法(包括列表、画树状图)计算一个简单事件的概率,进而判断游戏的公平性或进行决策.概率问题重在理解,模型思想值得关注 复习时,要把重点放在: 概率概念的理解上,指导学生认真分析概率的模型上,让他们分清是一步还是二步,甚至三步,是放回还是不放回,然后选择合理的列举方式展示事件的所有等可能结果,为概率的计算,甚至判断与决策奠定基础.夯实四基,对比研究,明确方向,刻苦拼搏。1. 深刻领会课程标准,准确分析学生现状 现实生活中存在着大量的数据需要整理,并提取有价值的信息;也包含着大量的随机现象需要分析,为人们认识客观世界提供了重要的思维模式和解决问题的方法,所以,统计与概率和现实生活紧密相连,必然是初中数学的核心内容,自然成为必考对象.夯实四基,对比研究,明确方向,刻苦拼搏。 尽管全国各地已经出现了将代数、几何、统计、概率等领域的知识相结合的试题,但是我们没必要因此而无限加大统计与概率知识的难度.实际上,只要我们理解了概率的本质,掌握了数据处理的基本方法,其他知识的引入仍然不会干扰学生解题. 因此,我们在进行统计与概率领域的复习时,不必进行过多的联系,而应该踏踏实实地加强基础知识、基本技能和基本思想方法的教学,重视学生基本活动经验的积累,只要能覆盖考试要求中所涉及到的各个知识点,并达到了相应的能力要求即可.2.准确把握考试要求,知识讲解适当有度夯实四基,对比研究,明确方向,刻苦拼搏。3.复习时间不宜过长,培养兴趣提高能力 统计与概率领域的复习时间应根据学生的掌握情况而定,但总体上不宜太长.按“三轮复习”建议:第一轮复习要细要全,第二轮要精要专,第三轮主要是通过模拟考试进行考查、落实.要注意“三轮复习”中,各阶段复习目的不同,复习角度和方法也不相同. 三轮复习决不能机械重复,而是一个螺旋上升,逐步培养能力的过程.同时要让学生认识到本领域的现实价值,教师尽可能变化习题背景,借鉴其它省市的优秀试题,提高复习兴趣.夯实四基,对比研究,明确方向,刻苦拼搏。 在复习过程中,不能一讲到底,要关注学生存在的问题,一定要对学生易犯的错误反复纠正、反复练习,不留死角.要做到:会题不错,题不二错;总结规律,举一反三.同时我们的老师要站的高一些,把握一个“度”字.4.精讲精练注重反思好的“方法”中考复习指导 数学教学应根据具体的教学内容,注意使学生在获得间接经验的同时也能够有机会获得直接经验,即从学生实际出发,创设有助于学生自主学习的问题情境,引导学生通过实践、思考、探索、交流等,获得数学的基础知识、基本技能、基本思想、基本活动经验,促使学生主动地、富有个性地学习,不断提高发现问题和提出问题的能力、分析问题和解决问题的能力。
《课程标准(2011版)P42》好的“方法”中考复习指导.1从学生的实际出发(1)态度决定一切(3)针对性练习(4)以考代练——模拟考试(2)手把手的教2.2好的“方法”2.图形与几何的中考复习指导.2立足课堂精编精讲,关注思维按部就班,夯实基础讲练结合,积累经验作业适度,反思调整2.2好的“方法”2.图形与几何的中考复习指导.3智慧复习(1)成功的数学教学,不能只让学生“做”,更应引导学生“想”,最终让学生“悟”。
(2)我们的教育目的不是在培养“解题的机器”,而是让学生学会分析问题和应用数学思想方法解决问题的方法。
2.具体内容与考试要求细目列表的变化。
3.样题的变化。
4.题型示例的变化。
?二、我校初三年级数学备课总复习工作计划 1.分三轮进行总复习,时间按4∶2∶1比例进行。
2.加强培优,辅差工作。
3.学校每月一考,备课组半月一考,班级每周一考。
4.加强集体备课,分块由每个老师准备相关内容。
?
初三数学复习计划交流a、统一思想认识,调整好心态: 1、使所学知识系统化、结构化,将初中三年的数学知识连成一个有机整体,利于学生理解,掌握和灵活运用;2、精讲多练,巩固基本技能,提高运算能力;3、抓好方法教学,引导学生归纳、总结解题的方法与技巧,提高解题能力; 4、做好综合题训练,提高学生综合运用知识分析问题的能力 ;b、集体备课,明确复习思路: 复习策略是两条腿走路: 一是选一本有知识点、又有2016年中考真题的资料进行第一轮分块复习,做到每个知识点都测试批改,要求学生过关 ;二是每周一套中考模拟题测试复习。 c、制定复习目标,激发学生积极参与: 制定班级目标、帮学生正确定位找准目标; 口号:每天进步一点 ;誓言:我们不比基础比进步,不比聪明比刻苦,不比昨天比今天; 理念:不抛弃、不放弃每一个学困生 。 d、制定复习措施: 1、认真钻研教材,根据课标及考纲,明确复习重点;要认真研究云南省初中学业水平标准与考试说明;2、从易到难复习让学生看到希望。 e、细节是重点,基础是关键。
1、在复习中要梳理知识:在梳理过程中,回归教材,挖掘教材中的例题、习题,通过一题多解,一题多变的变式训练增强学生训练的兴趣; 例1 如图 ,已知: 为 角平分线上一点,
于 ,以 为圆心, 为半径作圆。
求证: 是⊙ 的切线。思路1:连接OE,证△AOD≌△AOE
得∠ADO= ∠AEO=90°从而得证。
可以吗?说出理由?一题多解 例1 如图 ,已知: 为 角平分线上一点,
于 ,以 为圆心, 为半径作圆。
求证: 是⊙ 的切线。思路2:作OE⊥AC,证△AOD≌△AOE
得OD=OE从而得证。
可以吗?你还有更简捷的证法吗?一题多解 例1 如图 ,已知: 为 角平分线上一点,
于 ,以 为圆心, 为半径作圆。
求证: 是⊙ 的切线。一题多解思路3:过O作OE⊥AC于E
∵ AO平分∠BAC
OD⊥AB
∴ OE=OD
∵ OE是⊙O的半径
∴ AC是⊙O的切线
练习2 如图,AB是⊙O 的直径,⊙O交BC的中点于D,
DE⊥AC.
求证:DE与⊙O相切.一题多解变式训练变式1 昆明)如图,已知AB是⊙O的直径,过点E的直线EF与AB的延长线交于点F,AC⊥EF,垂足为C,AE平分∠FAC。
求证:CF是⊙O的切线。(5分)变式2 (广州) 如图,∠C=90o,BD平分∠ABC,DE⊥BD ,设⊙O是△BDE的外接圆。
求证:AC是⊙O的切线。DE⊥BD ,设⊙O是△BDE的外接圆变式训练e、细节是重点,基础是关键。
2、在复习中要注重查缺补漏:要求学生准备一本错题本,把每次测试的错题抄下来改正,便于复习,避免下次犯同样的错误,我们老师也应该准备一本错题本,便于出每日一练题,抓知识点过关; e、细节是重点,基础是关键。
3、抓数学“双基”,要求“会”就要做“对”;e、细节是重点,基础是关键。
4、教会学生从自己的实际情况出发,算分复习,寻找得分点、寻找突破点;5、解题时要培养学生:
①先想后算,审清题目,避免盲目;
②多想少算,理清思路,少走弯路;
③反思巧算,解法优化,过程完整不丢分;
④难度题不说我不会,要说我会多少,分步得分,养成有问必答的习惯; e、细节是重点,基础是关键。
6、过记忆关时可用顺口溜:如:完全平方公式可记为:首加末的完全平方等于首方加末方,首末积的2倍放中央;负指数幂可记为底倒指正;方差可记为偏差的平方的平均数;特殊角300、450、600的三角函数值可记为正弦、余弦的分母都是2,正切的分母都是3,它们的分子分别是根号下1、2、3,3、2、1、,3、9、27;f、摆脱题海归纳出解题规律。1.要想让学生从题海中解脱出来,我们老师就得进入题海去精选有代表性的题目; 2.做题要关注思路、方法、技巧,要注重发现题与题之间的内在联系。要通过比较,发现规律,做到触类旁通,做一题会一类; 3.复习方法要多样化,但每个知识点进行测试批分一定可以激起学生的复习兴趣; g、规范答题格式:1、抓书写;2、抓答题格式:从左至右、从上到下、写出关键理由; 17.(昆明)(6分)如图,点B、D、C、F在一条直线上,且BC = FD,AB = EF.
(1)请你只添加一个条件(不再加辅助线),使△ABC≌△EFD,你添
加的条件是 ;
(2)添加了条件后,证明△ABC≌△EFD.AC=DE……1分……2分……3分……4分……5分中考要求列表法求概率如下(规范格式):中考要求树形图求概率如下(规范格式):g、规范答题格式:3、抓有问必答:特别强调统计题中的有问必答; 4、每个题型都让学生了解评分标准,让学生按评分标准规范答题,平时批试卷时要给过程分。(1)证明:连接OE……………1分
∵AE平分∠FAC
∴∠CAE=∠OAE
又∵OA=OE,
∴ ∠OEA=∠OAE …………..…2分
∴ ∠CAE=∠OEA
∴OE∥AC…………………....…3分
∴∠OEF=∠ACF
又∵AC⊥EF
∴∠OEF=∠ACF=90°
∴OE⊥CF …………………...…4分
又∵点E在⊙O上
∴CF是⊙O的切线…………..…5分
(昆明24题)看看你能得几分?h、复习中要抓好培优辅差工作:对优等生的要求是:
1.课堂上跟老师走;负责帮助一名后进生;看错题本,避免犯同样的错误;
2.每天做一题压轴题,注重把握解题方法、解题思路;切忌死钻偏题、怪题;
3.每周完成一套中考模拟题,提高应试能力;
4.参加年级统一组织的培优辅导。h、复习中要抓好培优辅差工作:对学困生的要求是:
1.课堂跟老师走,寻找自己的强项;
2.组织师徒结对,不懂的随时问师傅问老师;看得分本,寻找得分点,突破点,按自己的目标分可以算分复习;
3.每周完成一套中考模拟题,提高应试能力。基础题分分必争,难度题分步得分,要舍得放弃;
4.参加年级组织的基础过关辅导;三、如何有实效的帮助学生提高数学成绩1.不同时期的教与学。
2.想尽一切办法调动学生学习积极性。
3.掌握好共性与个性的问题处理。
4.有条件实现一对一进行个性问题的分析讲解,有重点分小组实现水平升级。四、2016年考试方向预测和对考生的几点复习与应试的建议 1.全面夯实教学基础知识,构建完善的知识体系。
2.科学确定复习目标,合理安排复习时间和复习内容。
3.精选例体,及时总结解题的经验教训。
4.注意实际应用问题,强调操作实践。
5.注意开放探究,形成数学能力。
?
五、教学反思与教学建议 1.认真落实初中数学基础知识,基本运算教学。
2.从初一开始就重视每一堂课的教学。
3.重视、加强几何的教学。
4.重视对应用问题的教学。
5.要养成书写有条理、工整、整洁的良好学习习惯。
6.加强对数学学习较困难的学生帮助和指导
7.在复习工作中重视教材。
统计与概率部分的复习策略
一、明确依据和方向
二、对比分析 挖掘本质
三、中考复习策略和方法
统计与概率部分的复习策略夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。一、明确依据和方向二、对比分析 挖掘本质三、中考复习策略和方法夯实四基,对比研究,明确方向,刻苦拼搏。一、明确依据和方向 夯实四基,对比研究,明确方向,刻苦拼搏。 我省中考试题是以《云南省学业水平标准与考试说明》为依据来命制的,因此,我们必须认真研读《考试说明》,准确理解和把握考试要求,从而更加高效地进行我们的复习备考工作.1.统计与概率领域的课标要求1.1 内容标准: “统计与概率”主要研究现实生活中的数据和客观世界中的随机现象,它通过对数据收集、整理、描述和分析以及对事件发生可能性的刻画,来帮助人们作出合理的推断和预测.夯实四基,对比研究,明确方向,刻苦拼搏。1.2 总体要求:学生将体会抽样的必要性以及用样本估计总体的思想,进一步学习描述数据的方法,进一步体会概率的意义,能计算简单事件发生的概率. 夯实四基,对比研究,明确方向,刻苦拼搏。1.3 教学要求:
①应注重所学内容与日常生活、自然、社会和科学技术领域的联系,使学生体会统计与概率对制定决策的重要作用;
②应注重使学生从事数据处理的全过程,根据统计结果作出合理的判断;
③应注重使学生在具体情境中体会概率的意义;
④应加强统计与概率之间的联系;
⑤应避免将这部分内容的学习变成数字运算的练习,对有关术语不要求进行严格表述. 夯实四基,对比研究,明确方向,刻苦拼搏。2.统计与概率领域的《中考说明》要求夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。夯实四基,对比研究,明确方向,刻苦拼搏。二、对比分析 挖掘本质夯实四基,对比研究,明确方向,刻苦拼搏。云南中考13—15年有关统计试题的比较分析夯实四基,对比研究,明确方向,刻苦拼搏。18.(7分)(2013?云南)近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图.
(1)求出本次被调查的学生数;
(2)请求出统计表中a的值;
(3)求各组人数的众数;
(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.
考点:扇形统计图;用样本估计总体;统计表;众数.
分析:(1)根据A组有12人,占被调查总数的10%,据 此即可求得总人数;
(2)总人数减去其它各组的人数即可求得;
(3)根据众数的定义即可求解;
(4)利用2400乘以对应的比例即可求解.
夯实四基,对比研究,明确方向,刻苦拼搏。5.(3分)(2013?昆明)为了了解2013年昆明市
九年级学生学业水平考试的数学成绩,
从中随机抽取了1000名学生的数学成绩.
下列说法正确的是( ) 本题考查了总体、个体、样本、样本容量的知识,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
点评18.(5分)(2013?昆明)2013年6月6日第一届南亚博览会在昆明举行.某校对七年级学生开展了“南博会知多少?”的调查活动,采取随机抽样的方法进行问卷调查,问卷调查的结果分为“不太了解”、“基本了解”、“比较了解”、“非常了解”四个等级,对调查结果进行统计后,绘制了如下不完整的条形统计图:
根据以上统计图提供的信息,回答下列问题:(1)若“基本了解”的人数占抽样调查人数的25%,此次调查抽取了 学生;
(2)补全条形统计图;
(3)若该校七年级有600名学生,请估计“比较了解”和“非常了解”的学生共有多少人?考点:条形统计图;用样本估计总体.专题:计算题.分析:(1)由“基本了解”的人数除以所占的百分比即可得到调查的学生数;(2)根据学生总数求出“比较了解”的学生数,补全条形统计图即可;(3)求出“比较了解”和“非常了解”的学生在样本中所占的百分比,乘以600即可得到结果.8.(3分)(2014年云南省)学校为了丰富学生课余活动开展了一次“爱我云南,唱我云南”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
成绩(分) 9.40 9.50 9.60 9.70 9.80 9.90
人数 2 3 5 4 3 1
则入围同学决赛成绩的中位数和众数分别是( )
A. 9.70,9.60 B. 9.60,9.60
C.9.60,9.70 D. 9.65,9.60考点: 众数;中位数.
分析: 根据中位数和众数的概念求解.
解答: 解:∵共有18名同学,
则中位数为第9名和第10名同学成绩的平均分,即中位数为:=9.60,
众数为:9.60.
故选B.点评: 本题考查了中位数和众数的概念,一组数据中出现次数最多的数据叫做众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.18.(9分)(2014年云南省)为了解本校九年级学生期末数学考试情况,销量在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?考点: 条形统计图;用样本估计总体;扇形统计图.
分析: (1)抽查人数可由C等所占的比例为50%,根据总数=某等人数÷比例来计算;
(2)可由总数减去A、C、D的人数求得B等的人数,再补全条形统计图;
(3)用样本估计总体.用总人数1200乘以样本中测试成绩等级在80分(含80分)以上的学生所占百分比即可.解答: 解:(1)20÷50%=40(人),
答:这次随机抽取的学生共有40人;
(2)B等级人数:40﹣5﹣20﹣4=1(人)
条形统计图如下:
(3)1200××100%=480(人),
答:这次九年级学生期末数学考试成绩为优秀的学生人数大约有480人.点评: 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.7.(2015云南省)为加快新农村试点示范建设,我省开展了“美丽乡村”的评选活动,下表是我省六个州(市)推荐候选的“美丽乡村”个数统计结果:
在下表统计的数据中,平均数和中位数分别( )
A.42,43.5 B. 42,42 C.31,42 D.36,54夯实四基,对比研究,明确方向,刻苦拼搏。云南中考13—15年有关概率试题的比较分析19.(6分)(2013?昆明)有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线上y= 上的概率.
考点:列表法与树状图法;反比例函数图象上点的坐标特征.专题:图表型.分析:(1)画出树状图即可得解;(2)根据反比例函数图象上点的坐标特征判断出在双曲线上y= 上的情况数,然后根据概率公式列式计算即可得解.解答:解:(1)根据题意画出树状图如下:;(2)一共有9种等可能的情况:(-1,-1),(-1,1),(-1,2),(1,1),(1,-1),(1,2),(2,2),(2,-1),(2,1),点(x,y)落在双曲线上y= 上的有2种情况:(1,2),(2,1)所以,P= 19.(7分)(2014年云南省)某市“艺术节”期间,小明、小亮都想去观看茶艺表演,但是只有一张茶艺表演门票,他们决定采用抽卡片的办法确定谁去.规则如下:
将正面分别标有数字1、2、3、4的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上,随机抽出一张记下数字后放回;重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字.如果两个数字之和为奇数,则小明去;如果两个数字之和为偶数,则小亮去.
(1)请用列表或画树状图的方法表示抽出的两张卡片上的数字之和的所有可能出现的结果;
(2)你认为这个规则公平吗?请说明理由.考点: 游戏公平性;列表法与树状图法.
分析: (1)用列表法将所有等可能的结果一一列举出来即可;
(2)求得两人获胜的概率,若相等则公平,否则不公平.
解答: 解:(1)根据题意列表得:
1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8(2)由列表得:共16种情况,其中奇数有8种,偶数有8种,
∴和为偶数和和为奇数的概率均为0.5,
∴这个游戏公平.
点评: 本题考查了游戏公平性及列表与列树形图的知识,难度不大,是经常出现的一个知识点.20.(2015云南省)现有一个六面分别标有数字1,2,3,4,5,6且质地均匀的正方体骰子,另有三张正面分别标有数字1,2,3的卡片(卡片除数字外,其它都相同).先由小明投骰子一次,记下骰子向上一面出现的数字,然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张,记下卡片上的数字.
(1)请用列表或画树形图(树状图)的方法,求出骰子向上一面出现的数字与卡片上的数字之积为6的概率;
(2)小明和小王做游戏,约定游戏规则如下:若骰子向上一面出现的数字与卡片上的数字之积大于7,则小明赢;若骰子向上一面出现的数字与卡片上的数字之积小于7,则小王赢.问小明和小王谁赢的可能性更大?请说明理由.夯实四基,对比研究,明确方向,刻苦拼搏。三、中考复习策略与方法夯实四基,对比研究,明确方向,刻苦拼搏。全面撒网——形成知识体系夯实四基,对比研究,明确方向,刻苦拼搏。 可以预测:2016年对于统计的考查和前几年的变化不会很大,依然会以一小一大的形式出现,大题8分小题4分,备考时要关注:统计量的计算、从统计图中获取信息,再进行处理信息,从而解决问题. 复习时,要把重点放在:统计概念的理解上,学生读图识图及从图中获取数据信息、进而处理信息的能力的培养上.把各种统计图表相结合让学生读取,读取时注意表(图)头,图中所涉及的量及各种信息,如:各数据之间的关系等.逐步培养统计观念,提高信息处理能力 夯实四基,对比研究,明确方向,刻苦拼搏。2.
概
率夯实四基,对比研究,明确方向,刻苦拼搏。古典概型的概率计算——重点运用列举法(包括列表、画树状图)计算简单事件发生的概率涉及频率估计概率和几何概型的概率计算 理解频率与概率的关系,通过几何图形的面积求概率夯实四基,对比研究,明确方向,刻苦拼搏。 可以预测:2016年的概率试题依然会以8分的解答题出现,备考时,依然要关注:借助列举法(包括列表、画树状图)计算一个简单事件的概率,进而判断游戏的公平性或进行决策.概率问题重在理解,模型思想值得关注 复习时,要把重点放在: 概率概念的理解上,指导学生认真分析概率的模型上,让他们分清是一步还是二步,甚至三步,是放回还是不放回,然后选择合理的列举方式展示事件的所有等可能结果,为概率的计算,甚至判断与决策奠定基础.夯实四基,对比研究,明确方向,刻苦拼搏。1. 深刻领会课程标准,准确分析学生现状 现实生活中存在着大量的数据需要整理,并提取有价值的信息;也包含着大量的随机现象需要分析,为人们认识客观世界提供了重要的思维模式和解决问题的方法,所以,统计与概率和现实生活紧密相连,必然是初中数学的核心内容,自然成为必考对象.夯实四基,对比研究,明确方向,刻苦拼搏。 尽管全国各地已经出现了将代数、几何、统计、概率等领域的知识相结合的试题,但是我们没必要因此而无限加大统计与概率知识的难度.实际上,只要我们理解了概率的本质,掌握了数据处理的基本方法,其他知识的引入仍然不会干扰学生解题. 因此,我们在进行统计与概率领域的复习时,不必进行过多的联系,而应该踏踏实实地加强基础知识、基本技能和基本思想方法的教学,重视学生基本活动经验的积累,只要能覆盖考试要求中所涉及到的各个知识点,并达到了相应的能力要求即可.2.准确把握考试要求,知识讲解适当有度夯实四基,对比研究,明确方向,刻苦拼搏。3.复习时间不宜过长,培养兴趣提高能力 统计与概率领域的复习时间应根据学生的掌握情况而定,但总体上不宜太长.按“三轮复习”建议:第一轮复习要细要全,第二轮要精要专,第三轮主要是通过模拟考试进行考查、落实.要注意“三轮复习”中,各阶段复习目的不同,复习角度和方法也不相同. 三轮复习决不能机械重复,而是一个螺旋上升,逐步培养能力的过程.同时要让学生认识到本领域的现实价值,教师尽可能变化习题背景,借鉴其它省市的优秀试题,提高复习兴趣.夯实四基,对比研究,明确方向,刻苦拼搏。 在复习过程中,不能一讲到底,要关注学生存在的问题,一定要对学生易犯的错误反复纠正、反复练习,不留死角.要做到:会题不错,题不二错;总结规律,举一反三.同时我们的老师要站的高一些,把握一个“度”字.4.精讲精练注重反思好的“方法”中考复习指导 数学教学应根据具体的教学内容,注意使学生在获得间接经验的同时也能够有机会获得直接经验,即从学生实际出发,创设有助于学生自主学习的问题情境,引导学生通过实践、思考、探索、交流等,获得数学的基础知识、基本技能、基本思想、基本活动经验,促使学生主动地、富有个性地学习,不断提高发现问题和提出问题的能力、分析问题和解决问题的能力。
《课程标准(2011版)P42》好的“方法”中考复习指导.1从学生的实际出发(1)态度决定一切(3)针对性练习(4)以考代练——模拟考试(2)手把手的教2.2好的“方法”2.图形与几何的中考复习指导.2立足课堂精编精讲,关注思维按部就班,夯实基础讲练结合,积累经验作业适度,反思调整2.2好的“方法”2.图形与几何的中考复习指导.3智慧复习(1)成功的数学教学,不能只让学生“做”,更应引导学生“想”,最终让学生“悟”。
(2)我们的教育目的不是在培养“解题的机器”,而是让学生学会分析问题和应用数学思想方法解决问题的方法。
同课章节目录
