考向一 抛体运动-2025年高考物理专题复习课件
文档属性
| 名称 | 考向一 抛体运动-2025年高考物理专题复习课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-02-18 00:00:00 | ||
图片预览








文档简介
(共67张PPT)
专题四 曲线运动
考向一 抛体运动
2025年高考物理专题复习资料
考点切片
考点1 运动的合成与分解
题组1 合运动与分运动
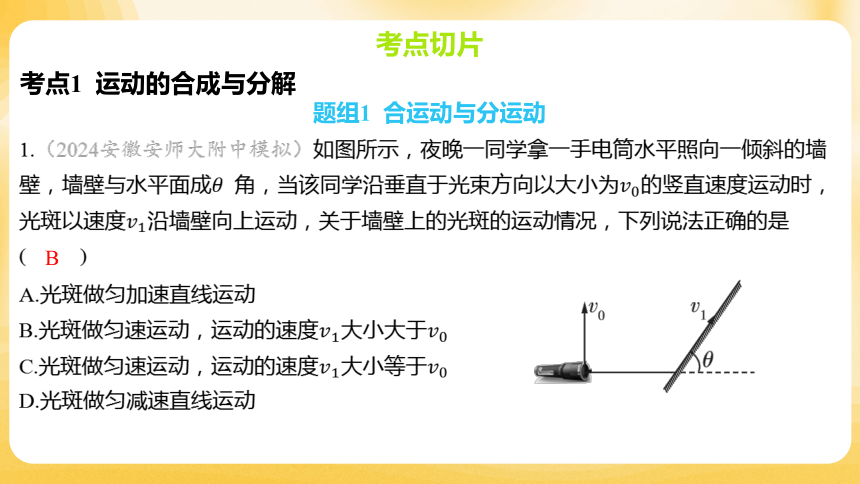
1.(2024安徽安师大附中模拟)如图所示,夜晚一同学拿一手电筒水平照向一倾斜的墙
壁,墙壁与水平面成 角,当该同学沿垂直于光束方向以大小为 的竖直速度运动时,
光斑以速度 沿墙壁向上运动,关于墙壁上的光斑的运动情况,下列说法正确的是
( )
B
A.光斑做匀加速直线运动
B.光斑做匀速运动,运动的速度大小大于
C.光斑做匀速运动,运动的速度大小等于
D.光斑做匀减速直线运动
【解析】 光斑的运动为合运动,其速度的竖直分量等于手电筒的运动速度,根据
运动的合成与分解知识可知,解得光斑的速度 ,故光斑做匀速运动,
运动的速度大于 。
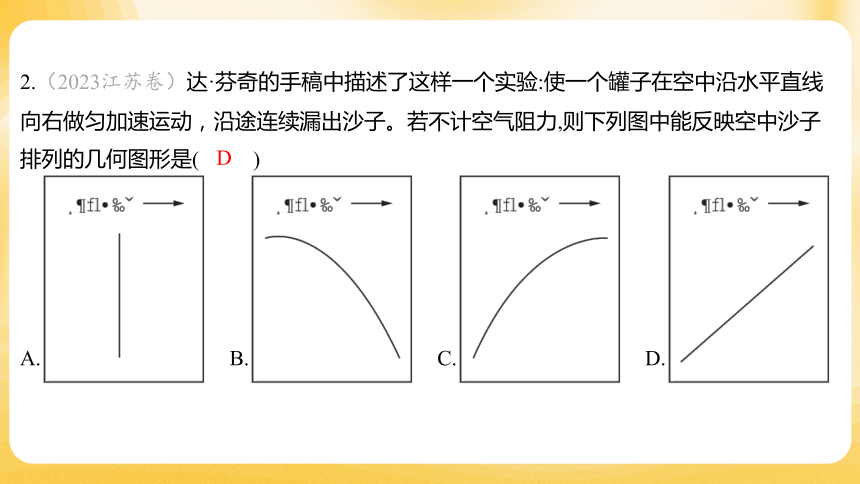
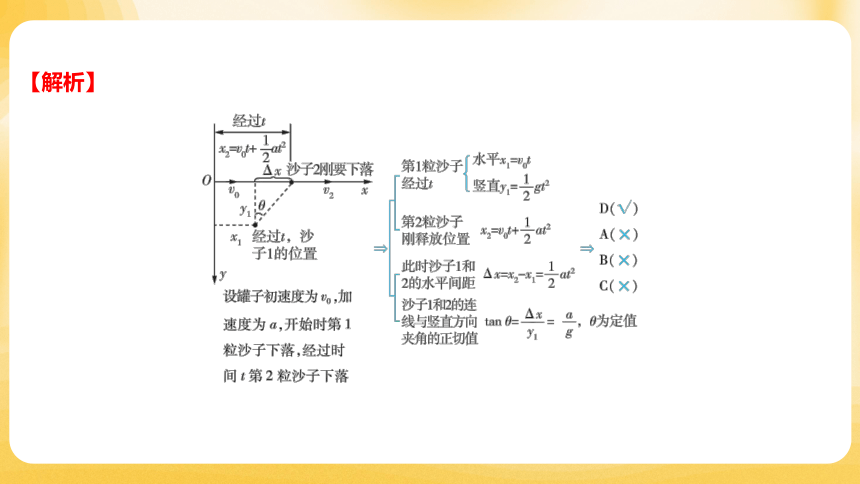
2.(2023江苏卷)达·芬奇的手稿中描述了这样一个实验:使一个罐子在空中沿水平直线
向右做匀加速运动,沿途连续漏出沙子。若不计空气阻力,则下列图中能反映空中沙子
排列的几何图形是( )
D
A. B. C. D.
【解析】
题组2 小船过河问题
解题觉醒
1.题型特征:求解小船过河的最短时间、最短位移问题。
2.解题技巧
(1)如果要以最短时间过河,让船速方向与河岸垂直,设河宽为
(2)如果要以最短位移过河。第一步:求
角,
移,过河时间
3.[多选](2025山东烟台阶段练习)随着强降雨季节的临近,各地开展“防溺水、强
救援”应急演练活动。如图所示,在某段平直河流的中心有遇险人员 (随水流向下游漂
移)等待救援,救援人员在岸边点( 垂直河岸)驾驶冲锋舟以最短时间救上遇险人
员 后,冲锋舟实时调整航向以最短距离回到岸边。已知冲锋舟在静水中的速度
,河中某处水流速度大小与到岸边距离 成正比,水流方向与河岸平行,
已知河中央水流速度为,到岸边的距离为 。下列说法正确的是( )
BC
A.前往河中央的过程中,冲锋舟的运动轨迹为直线
B.从岸边到达救援地点最少需要
C.从救援地点返回的过程中,冲锋舟行驶的路程为
D.返回岸边时,冲锋舟的速度大小为
【解析】 冲锋舟前往救援地点过程中,要求时间最短,需要船头垂直河岸,冲锋
舟在水中参与了一个匀速直线运动和一个匀变速直线运动(【点拨】由题意可得前往河
中央的过程中,有,其中 为常量,可知在平行河岸方向上冲锋舟做匀
加速直线运动。),故合运动轨迹为曲线。
从岸边到达救援地点需要的最短时间 。
从救援地点返回过程中,要求位移最短,由于冲锋舟在静水中速度大于水流速度
(【点拨】由题意可知冲锋舟在静水中的速度大于河中央水流速度,因此返回过程中冲
锋舟在静水中速度始终大于水流速度),冲锋舟在静水中速度沿河岸方向的分速度可以
和水流速度抵消,故冲锋舟的实际速度可以始终垂直于河岸,因此最短位移为
(【大招运用】根据大招内容中口诀“船快取河宽,水快除以余弦”,返回过程中冲锋舟
在静水中速度始终大于水流速度,则最短位移为 。)。
. .
冲锋舟回到岸边时,水流速度为零,冲锋舟速度大小为其在静水中的速度 。
4.[多选](2024黑龙江哈师大附中月考)如图所示,甲、乙两船在同一条河流中同时
开始渡河,河宽为,、分别是甲、乙两船的出发点,两船头与河岸均成 角,甲
船船头恰好对准点的正对岸点,经过一段时间乙船恰好到达 点。如果两船在静水中
速度大小均为 ,且两船相遇不影响各自的航行,下列判断正确的是( )
AD
A.水流方向向右,速度大小为
B.甲船沿河岸方向位移大小为
C.甲、乙两船不会在 上某点相遇
D.两船同时到达河对岸,花费时间均为
【解析】 由于乙船恰好到达 点,则可知水流方向向右,且乙船沿河岸方向的分
速度大小恰好等于水流的速度大小,即 。
甲、乙两船在垂直于河岸方向的分速度均为 ,因此到达对岸的时间均
为,甲船沿河岸方向位移大小 ,联立解得
。
由于乙船沿运动,甲船船头恰好对准点的正对岸 点(【点拨】甲船在静水中
的运动方向由指向。),在水流的作用下,甲船到达对岸时,应在 点的右侧,而
两船在垂直于河岸方向速度相同,一定会相遇,且在 上某点相遇(【点拨】乙船实
际运动为沿着虚线到达对岸点,则两船相遇点一定在 上。)。
. .
. .
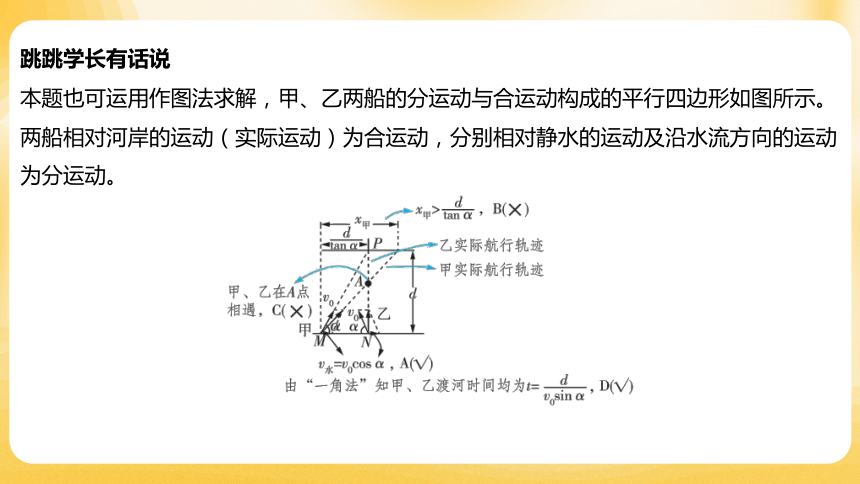
跳跳学长有话说
本题也可运用作图法求解,甲、乙两船的分运动与合运动构成的平行四边形如图所示。
两船相对河岸的运动(实际运动)为合运动,分别相对静水的运动及沿水流方向的运动
为分运动。
题组3 关联速度问题
解题觉醒
1.题型特征:用绳、杆等连接的两物体,求解关联物体的速度。
2.解题步骤
(1)画出绳、杆等两端的实际速度;
(2)将两端的实际速度分别沿绳(或杆)方向和垂直于绳(或杆)方向正交分解;
(3)利用两物体沿绳(或杆)方向速度大小相等,求实际速度大小关系。
5.(2025江苏前黄高级中学开学考)影视作品中的武林高手展示轻功时都是吊威亚
(钢丝)的。如图所示,轨道车通过细钢丝跨过滑轮拉着特技演员 上升,便可呈现
出演员飞檐走壁的效果。轨道车沿水平地面以速度大小 向左匀速前进,某
时刻连接轨道车的钢丝与水平方向的夹角 为 ,连接特技演员 的钢丝竖直,取
, ,则下列说法正确的是( )
A
A.该时刻特技演员 有竖直向上的加速度
B.该时刻特技演员 处于失重状态
C.该时刻特技演员的速度大小为
D.该时刻特技演员的速度大小为
【解析】 将车速 沿着细钢丝方向和垂直于细钢丝的方向分解,沿着细钢丝
方向的分速度与特技演员的速度大小相等,即 ,其中车速 不变,
随着小车向左运动, 不断减小,则不断增大,即特技演员 有竖直向上的加速度,
处于超重状态。
当 时,特技演员的速度大小为 。
6.[多选](2024广东深圳中学检测)如图所示,有一个水平向
左做匀速直线运动的半圆柱体,速度为 ,半圆柱体上有一根能
沿竖直方向运动的竖直杆,在竖直杆未下降到地面之前,杆同半
圆柱体接触点和柱心的连线与竖直方向的夹角为 ,杆的速度
为 ,下列说法正确的是( )
AD
A.竖直杆向下做加速直线运动 B.竖直杆向下做减速直线运动
C. D.
【解析】 设杆受半圆柱体的弹力为 ,将半圆柱体和杆的
速度分别沿弹力 所在的直线方向与杆同半圆柱体
接触点的切线方向分解,如图所示。 因为两接触运动物体沿接触弹
力方向的分速度大小相等(【点拨】所谓接触就是在接触面的垂线
方向二者没有相对运动,你走多少我走多少,否则就要分开,所以
在接触面的垂线方向分速度大小相等。),所以有
,则 ,杆向下运动, 变大, 变大, 变大,
杆做加速直线运动。
根据 ,得 。
7.(2024河南郑州第十一中学月考)如图所示,一根长直轻杆两端
分别固定小球和 ,竖直放置,两球半径忽略不计。由于微小的
扰动,球沿竖直光滑槽向下运动, 球沿水平光滑槽向右运动,
当杆与竖直方向的夹角为 时(图中未标出),关于两球速度
与 的关系正确的是( )
C
A. B. C. D.
【解析】 当杆与竖直方向的夹角为 时,将两小球的实际
速度沿杆方向和垂直于杆方向正交分解,如图所示,沿杆方
向两分速度大小相等,则 , ,
C正确。
考点2 平抛运动
题组1 平抛运动的基本规律
8.[多选](2025河北承德部分学校摸底)两位同学做平抛实验时,一
位同学将一小球水平抛出,另一位同学进行频闪照相,闪光频率为 。
已知小球在抛出瞬间闪光灯恰好闪光,如图所示, 为小球抛出瞬间的影
像,和之间、和之间均有1个影像未画出, 连线与水平方向的夹
角为 ,重力加速度取 ,不计空气阻力。下列说法正确的是
( )
AC
A.线段的长度为 B.小球的初速度大小为
C.线段的长度为 D.对应时的小球速度大小为
【解析】
解题第2季武林大会
分析平抛运动时,也可以利用数学方法,联立平抛运动方程、 ,得到
这个不含的平抛轨迹方程,代入轨迹上点的坐标,直接求出初速度 。
——广东湛江一中 王舶蘅
9.[多选](2023天津一中月考)投壶是从
先秦延续至清末的中国传统礼仪和宴饮游戏,
《礼记传》中提到:“投壶,射之细也。燕
饮有射以乐宾,以习容而讲艺也。”如图甲
BD
A.、两人所投箭的初速度大小之比为
B.、两人所投箭落入壶口时的速度大小之比为
C.、两人投射位置与壶口的水平距离之比为
D.、两人投射位置与壶口的水平距离之比为
所示,、 两人在不同位置沿水平方向各投出一支箭,如图乙、丙所示,箭尖插入壶
中时与水平面的夹角分别为 和 。已知两支箭质量相同,竖直方向下落的高度相
等。忽略空气阻力、箭长、壶口大小等因素的影响,下列说法正确的是
( )
【解析】 沿水平方向投出后,箭做平抛运动,两支箭竖直方向下落高度相等,则
两支箭在空中的运动时间相同(【点拨】箭在竖直方向上做自由落体运动,有
。 ),下落到瓶口时竖直方向上的速度相同,设箭尖插入壶中时与水平面的夹
角为, 箭投出时的初速度为,则,即 ,两支箭投出的初速度大
小之比为 。
设箭尖插入壶中时的速度大小为,则,即 ,两支箭落入壶口
时的速度大小之比为 。
因两支箭在空中的运动时间相同,甲、乙两人投射位置与壶口的水平距离之
比即初速度大小之比,为 。
10.(2023新课标卷)将扁平的石子向水面快速抛出,石子可能会在水面上一跳一跳地
飞向远方,俗称“打水漂”。要使石子从水面跳起产生“水漂”效果,石子接触水面时的速度
方向与水面的夹角不能大于 。为了观察到“水漂”,一同学将一石子从距水面高度为
处水平抛出,抛出速度的最小值为多少 (不计石子在空中飞行时的空气阻力,重力加
速度大小为 )
【答案】
【解析】 由题意可知石子接触水面前的运动可理想化为平抛运动,则其在竖直方向做
匀加速直线运动。从距水面高度为处水平抛出石子,由 可得,落到水面时其
竖直方向的速度为
要使石子落水时的速度方向与水面的夹角不大于 ,则
解得,即抛出速度的最小值 。
题组2 平抛运动的重要推论
解题觉醒
1.题型特征:题目中出现速度偏转角
夹角、速度反向延长线等关键词。
2.解题技巧
(1)
(2)速度反向延长线过水平位移中点。
11.(2025江苏南通阶段练习)如图所示,一小球从某高度处水平
抛出,经过时间到达地面时,速度与水平方向的夹角为 ,不计
空气阻力,重力加速度为 。下列说法正确的是( )
A
A.小球水平抛出时的初速度大小为
B.小球在时间内的位移与水平方向的夹角为
C.若小球初速度增大,则平抛运动的时间变长
D.若小球初速度增大,则 增大
【解析】 小球落地时竖直方向上的分速度为 ,因为落地时速度方向与水平
方向的夹角为 ,所以小球的初速度为 。
小球落地时速度方向与水平方向夹角的正切值 ,位移与水平方向夹角的
正切值,所以,但 (【大招运用】根据大招内容
中平抛运动的推论可知速度偏转角 的正切值等于位移偏转角 的正切值的2倍,可得
。)。
根据,解得 ,可知小球运动时间与下落高度有关,与初速度无关,
若小球初速度增大,则平抛运动的时间不变。
. .
小球落地时速度方向与水平方向夹角的正切值为 ,若小球初速度增大,
下落时间不变,则 将减小,即 减小。
12.(2025江苏淮安开学考)如图所示,半球面的半径为,球面上点与球心 等高,
小球先后两次从点以不同的速度、沿方向抛出,下落相同高度 ,分别撞击到
球面上、点。设上述两过程中小球运动时间分别为、 ,速度的变化量分别为
、 。则( )
C
A. B.
C.,式中为重力加速度 D.撞击 点时的速度方向与球面垂直
【解析】 小球两次均做平抛运动且下落高度相同,根据 可知,运动时间
相同。
根据 ,由于运动时间相同,所以速度变化量也相同。
设小球两次运动的水平位移分别为和,由几何关系可知 ,
,根据平抛运动规律,可知,,又有 ,联
立可得 。
若小球撞击点时的速度方向与球面垂直,则点速度方向的反向延长线过圆心 ,
根据平抛运动的推论,速度的反向延长线一定过水平位移的中点,而 点不是水平位移
的中点,与假设相矛盾,所以小球撞击 点时的速度方向与球面不垂直。
13.(2025重庆南开中学开学考)如图所示,一个质量为 的小球
从倾角为 的斜面顶端以速度水平向右抛出,重力加速度为 ,
斜面足够长,不计空气阻力,下列说法正确的是( )
D
A.从抛出小球开始计时,经过 后小球距离斜面最远
B.小球抛出的初速度越大,则小球落到斜面上的速度方向与水平
方向的夹角也越大
C.若小球还受到一个竖直向下的恒力,恒力大小与其重力大小相
等,则小球落到斜面上的速度大小为
D.若小球还受到一个位于竖直平面内的恒力(方向未知),且小
球抛出经过足够长的时间之后速度方向趋于与斜面平行,则该恒
力的最小值是
图1
【解析】 如图1所示,小球距离斜面最远时速度方向
与斜面平行(【点拨】将小球的速度沿平行斜面方向和垂
直斜面方向分解当小球垂直斜面方向的分速度为0时,小球
距离斜面最远,此时小球速度方向与斜面平行。),可得
,即 。
在平抛运动中,速度偏转角的正切值是位移偏转角正
切值的两倍。由于小球在斜面上抛出又落在斜面上,因此
在以不同初速度抛出的情况下位移偏转角相同,则速度偏转角相同。故增大初速度,速
度偏转角不变。
图2
若小球还受到一个竖直向下的恒力,恒力大小与其重
力大小相等,由牛顿第二定律可得 ,
则小球的加速度 ,分解小球落在斜面上的速度,如
图2所示,可得 ,
。
图3
如图3所示,经过足够长的时间,小球的速度趋于与斜
面平行,则合力的方向与斜面方向平行。由几何关系可知,
当恒力方向与合力方向垂直时,恒力最小,恒力的最小值
为 。
题组3 平抛运动的轨迹比较问题
解题觉醒
1.题型特征:给出两个平抛轨迹,比较物体的初速度和落地时间。
2.解题技巧:口诀“高度大时间长,同起点大压小,起点不同先平移”。
14.(2024重庆调研)甲、乙两球位于同一竖直线上的不同
位置,甲比乙高,如图所示,将甲、乙两球分别以、
的速度沿同一方向水平抛出,不计空气阻力,下列条件中
有可能使乙球击中甲球的是( )
D
A.同时抛出,且 B.甲比乙后抛出,且
C.甲比乙早抛出,且 D.甲比乙早抛出,且
【解析】 题图中,乙球击中甲球的条件是:水平位移相等,甲球竖直位移等于乙
球的竖直位移加上,甲球应先抛出,故有, ,联立解得
, 。
跳跳学长传妙招
应用大招口诀“高度大时间长”,可知甲的高度大,所需时间较长,若让两球相撞,则甲
要先抛出。将甲球轨迹向下平移至甲、乙两球的抛出点在同一点,如图中轨迹③所示。
根据“同起点大压小,起点不同先平移”,可知 。
15.(2024福建厦门一中检测)如图所示,轴在水平地面上, 轴沿竖直方向,图中画
出了从轴上沿轴正方向抛出的三个小球、和的运动轨迹,其中和 是从同一点抛
出的,不计空气阻力,则( )
B
A.的运动时间比的长 B.和 的运动时间相同
C.的初速度与的初速度可能相等 D.的初速度比 的小
【解析】 三个小球在竖直方向都做自由落体运动,根据 ,得
,比抛出时的高度低,则比运动的时间短;、抛出的高度相同,则和
运动的时间相同。
比运动的时间短,的水平位移大于的水平位移,则的初速度大于 的初速度。
、的运动时间相等,的水平位移大于的水平位移,则的初速度大于 的初速
度。
跳跳学长有话说
根据大招口诀“高度大时间长”,可知、的高度一样且大于的高度,则、 下落时间
相等,且大于的下落时间,A错误,B正确;将球轨迹向下平移至、 两球的抛出点
在同一点,如图中轨迹 所示。根据“同起点大压小,起点不同先平移”,可知
,C、D错误。
题组4 斜面平抛比例问题
16.(2024广西南宁期末)滑雪是一项非常刺激且具观赏
性的运动项目。如图所示,运动员甲、乙(视为质点)
从水平跳台向左分别以初速度和 水平飞出,最后都
落在着陆坡(可视为斜面)上,不计空气阻力,则运动
员从水平跳台飞出到落在着陆坡上的过程中,下列说法
正确的是( )
D
A.飞行的时间之比 B.水平位移之比
C.落到坡面上的瞬时速度大小相等 D.落到坡面上的瞬时速度方向相同
【解析】 设斜坡倾角为 ,则有,解得 ,
可知他们飞行时间之比为(【大招运用】根据大招内容中的口诀“之比
不变,只有位移要方”,由题意可知、水平位移之比 。)。
根据,可得他们飞行的水平位移之比为 。
根据平抛运动的推论:瞬时速度与水平方向夹角的正切值是位移与水平方向
夹角正切值的两倍,只要是落在坡面上,位移与水平方向夹角相同,所以两人落到坡面
上的瞬时速度方向一定相同,故落在坡面上的瞬时速度大小之比等于初速度大小之比,
为 。
. .
17.[多选](2024山西大同模拟)如图所示,质量相同的两小
球、分别从斜面顶端和斜面中点 沿水平方向抛出后,恰好
都落在斜面底端,不计空气阻力,下列说法正确的是( )
ACD
A.小球、在空中飞行的时间之比为
B.小球、抛出时的初速度大小之比为
C.小球、到达它们与斜面距离最大位置时的速度大小之比为
D.小球、到达斜面底端时速度大小之比为
【解析】 因为、两球下落的高度之比为,根据得 ,则飞行
的时间(【点拨】飞行时间仅由下落的高度决定。)之比为 。
、两球的水平位移之比为,运动时间之比为,根据 知,初速度大
小之比为 。
设斜面的倾角为 ,小球、到达它们与斜面距离最大位置时的速度为
(【点拨】此时小球速度方向与斜面方向平行。将小球速度沿水平方向和竖直方向进行
分解,即可得出此时小球速度与初速度的关系。),与初速度成正比,则小球、 到
达它们与斜面距离最大位置时的速度大小之比为 。
. .
小球落在斜面上时,速度方向与水平方向夹角的正切值是位移与水平方向夹角正
切值的2倍,因两小球都落在斜面上,故两小球的位移与水平方向的夹角相等,则两小
球到达斜面底端时的速度方向与水平方向的夹角也相等(【点拔】 “速度角”
“位移角”=“斜面角),设该夹角为 ,则 ,末速度大小与初速
度大小成正比,即小球、到达斜面底端时的速度大小之比为 。
题组5 平抛运动的临界问题
18.[多选](2024山西运城康杰中学检测)康杰中学举办的“学雷锋集爱
心”义卖活动中,有班级设置了套圈游戏,如图所示。某同学从距水平地
面高度处水平抛出一个半径为 的圆环,套前方地面上的水杯,
假设圆环运动过程中始终保持水平,圆环中心到水杯的水平距离为 ,
水杯高度为,水杯大小忽略不计。取 ,忽略空气阻力,要
想套住水杯,圆环刚抛出时的速度可以是( )
AB
A. B. C. D.
【解析】 已知圆环抛出时的高度,圆环的半径为 ,水杯的高度为
,圆环中心到水杯的水平距离为 ,根据平抛运动规律可知
,解得 ,(【点拨】无论圆环抛出时速度大小如何,圆环下落
高度一定,下落时间一定。)当圆环右侧贴着水杯落下时,圆环抛出时的初速度有最小
值,即,解得 ;当圆环左侧贴着水杯落下时,圆环抛出时的初
速度有最大值,即,解得 ,要使圆环套住地面上的水杯,圆环
刚抛出时的速度应该满足,故选 。
. .
. .
19.(2025辽宁鞍山一模)如图甲为一个网球场的示意图,一个网球发球机固定在边角
处,可以将网球沿平行于地面的各个方向发出,发球点距地面高度为,球网高 。
图乙为对应的俯视图,其中, 。按照规则,网球发出后不触网且落
在对面阴影区域(包含虚线)内为有效发球。图中虚线为球场的等分线,则发球机有效
发球时发出网球的最小速率为(忽略一切阻力,取 )( )
A
A. B. C. D.
【解析】 第一步:构建运动模型——平抛运动。
当发球机有效发球且发出网球的速率最小时,球应恰好到达有效区域的边缘,如答图所
示,设网球从点发出后落在 点。
第二步:化曲为直——即分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
网球从点发出后,在竖直方向做自由落体运动,有,解得 ,网球
恰不触网(【点拨】根据大招内容中的平抛轨迹比较口诀“高度大时间长,同起点大压
小,起点不同先平移”可知,发出网球的速率最小时,网球的运动轨迹应在最下边,因
此此情况下网球恰不触网。),则有,解得 ,网球在水平方向
上做匀速直线运动,则,因与 为相似三角形,则有
,因,,可得 ,
。
第三步:由水平方向的分运动求网球的最小速
率。
则发球机有效发球时发出网球的最小速率为
,A正确。
考点3 抛体运动的关联运动
20.[多选](2024黑龙江哈师大附中期中)如图所示,同一竖直平面内有四分之一圆
弧和倾角为 的斜面,、两点与圆弧的圆心 等高。现将甲、乙两小球分
别从、两点以初速度、沿水平方向同时抛出,两球恰好在 点相碰(不计空气阻
力),已知, 。下列说法正确的是( )
AD
A.初速度、大小之比为
B.若仅增大 ,则两球不再相碰
C.若大小变为原来的一半,则甲球恰能落在斜面的中点
D.若只抛出甲球并适当改变初速度大小,则甲球可能垂直击中
圆环
【解析】 设圆弧所在圆的半径为,甲、乙两球从等高处做平抛运动恰好在
点相碰,则运动时间相等,水平方向有, ,所以
。
【点拨】在 点相碰,说明两球的下落高度相等,则运动时间相等。
两球相碰,则满足,因两球始终在同一水平面上,故若仅增大 ,
显然存在 满足方程,两球会相碰。
若 大小变为原来的一半,在时间不变的情况下水平位移会变为原来的一半,但由
于甲球会碰到斜面,下落高度减小,时间减小,所以甲球的水平位移小于原来的一半,
不会落在斜面的中点。
如图所示,若甲球以速度水平抛出,垂直击中圆弧 ,则
落点速度的反向延长线过圆心 ,由几何关系有
, (【点拨】平
抛运动的解题规律就是位移分解方程和速度分解方程。),以上
两个方程有两个未知
数,可以求解和 ,因此只抛出甲球并适当改变初速度大小,甲球可能垂直击中圆弧
。
. .
21.(2024云南大理模拟)如图所示,将小球从点以速度水平抛出,同时将小球
从水平地面上的点以速度竖直上抛,、两个小球在同一竖直平面内运动,且在
点正上方的某一位置相遇。已知点到水平地面的高度为,、 两点的水平距离为
,、 两个小球可视为质点,空气阻力可忽略不计。则下列说法正确的是( )
C
A.、两个小球相遇时,小球 一定处于上升过程中
B.只改变小球的水平速度,、两个小球依旧能在 点
正上方相遇
C.、两个小球初速度必须满足
D.、 两个小球从抛出到相遇的过程中,两球的速度变化
量不相等
【解析】 小球做平抛运动,,若与相遇时下落的高度为,则 ,
小球做竖直上抛运动,,联立以上式子可得 。
、两个小球在上升、下降过程中或 到达最高点时均有可能相遇。
若只改变小球的水平速度,不再满足,、两个小球不可能在 点正上
方相遇。
、两个小球从抛出到相遇过程中,加速度均为重力加速度,运动时间 相等,
故速度的变化量 也相同。
考点4 类平抛运动
22.[多选](2024江西吉安白鹭洲中学模拟)一足够大且光滑的矩形斜面,倾角为 ,
高为,现有一小球在处沿平行于底边的初速度滑上斜面,最后从 处离开斜面。已
知重力加速度大小为 。下列说法正确的是( )
ABC
A.小球的运动轨迹为抛物线
B.小球的加速度大小为
C.小球从处到达处所用的时间为
D.小球从处到达处的位移大小为
【解析】 小球受重力和支持力两个力,合力沿斜面向下,与初速度方向垂直,小
球做类平抛运动,其运动轨迹为抛物线。
根据牛顿第二定律,有,解得 。
由几何关系得,小球沿加速度方向上的位移为,根据位移公式 ,
解得 。
小球在沿初速度方向的位移为,则小球从处到达 处的位移大
小为 。
23.(2025湖北新高考联考协作体开学考)如图所示,一物体在某液体中运动时只受到重
力和恒定的浮力的作用,且。如果物体从点以水平初速度 开始运动,最后
落在点,、间的竖直高度为,与右壁水平间距为,重力加速度为 ,则下列说
法正确的是( )
D
A.从运动到的时间为
B.与之间的水平距离为
C.若增大初速度 ,物体将可能撞击右壁,且初速度越大,物体
撞击右壁时的速度越大
D.若足够大,当初速度 时,物体撞击右壁时的速度最
小
【解析】 根据牛顿第二定律有,解得 ,该物体做类平抛运动,
则,解得物体从运动到的时间为 。
与之间的水平距离 。
根据大招内容中的平抛轨迹比较口诀“高度大时间长,同起点大压小,起点不
同先平移”可知,若增大初速度 ,物体将可能撞击右壁。物体撞击右壁时,物体运动
的时间为,物体在竖直方向的速度为 ,物体撞击右壁时的速度
,根据数学知识可知,当,即当初速度 时,
物体撞击右壁时的速度最小,故若增大初速度 ,物体将可能撞击右壁,撞击右壁时的
速度不一定越大。
跳跳学长敲黑板
有时物体的运动与平抛运动很相似,也是在某方向做匀速直线运动,在与之垂直的方向
做初速度为零的匀加速直线运动。这种运动,像平抛又不是平抛,通常称为类平抛运动。
处理方法与处理平抛运动方法一样,只是加速度 不同而已。
考点5 斜抛运动
24.(2023湖南卷)如图甲所示,我国某些农村地区人们用手抛撒谷粒进行水稻播种。某
次抛出的谷粒中有两颗的运动轨迹如图乙所示,其轨迹在同一竖直平面内,抛出点均为
,且轨迹交于点,抛出时谷粒1和谷粒2的初速度分别为和,其中方向水平, 方向
斜向上。忽略空气阻力,关于两谷粒在空中的运动,下列说法正确的是( )
B
图甲
图乙
A.谷粒1的加速度小于谷粒2的加速度 B.谷粒2在最高点的速度小于
C.两谷粒从到的运动时间相等 D.两谷粒从到 的平均速度相等
【解析】
只受重力→两谷粒加速度 ,A(×)
从到位移相同→谷粒2先上升后下降,用时更长,即 (×)
从到 位移相同
谷粒2在最高点只有水平速度
(【点拨】做斜抛运动的物体运动到最高点时其竖直方向速度为零。)
竖直方向
水平方向
谷粒合位移,
25.(2025陕西渭南阶段练习)如图所示,网球运动员训练时,运动员在同一高度的前
后两个不同位置、将网球斜向上击出后,网球恰好垂直击中竖直墙上的同一固定点 。
已知网球从运动到的时间为,重力加速度大小为 ,忽略空气阻力,下列说法正确
的是( )
C
A.从点击出的网球比从 点击出的网球的初速度小
B.若、两点间的距离为,则在、 两点的击球速度大
小之差为
C.在 点将网球击出时,若网球的速度方向与竖直方向的
夹角为 ,则点与墙面间的距离为
D.若、两点间的距离与、两点间的距离之比为 ,
则从、两点击出的网球的速度大小之比也为
【解析】 采用逆向思维,网球做平抛运动,根据 ,两【点拨】分析科抛
运动,只有物体运动到最高点,才能利用逆向思维将物体的运动看成反方向的平抛运动。
次高度相同,故网球在、两点时竖直方向的速度相同,根据,可得 ,
可知两球运动时间相同,而以轨迹1运动的水平位移大,在水平方向上,根据 可
知以轨迹1运动的水平速度比以轨迹2运动的水平速度大,根据可知从 点
击出的网球的初速度比从 点击出的网球的大。
采用逆向思维,网球做平抛运动,两球运动的时间相等,均为 ,在水平方向上有
,解得水平方向速度大小之差为 ,但在
、两点的击球速度在竖直方向有分量,故 。
采用逆向思维,网球做平抛运动,竖直方向的高度为 ,根据速度偏转角正
切值等于位移偏转角正切值的两倍,有 (【提醒】注意网球的速度方向与竖
直方向的夹角为0.而不是与水平方向的夹角为 。),解得 点与墙面间的距离为
。
若、两点间的距离与、两点间的距离之比为 ,两球运动时间相等,根据
平均速度的定义可知,从、 两点击出的网球在整个运动过程中的平均速度大小之比
也为 。
26.[多选](2025山东齐鲁名校联盟开学考)如图所示,从同一水平面上的、 两点
同时抛出两个小球、,出射速度与水平方向夹角分别为 和 ,两小球运动轨
迹在同一竖直面内,射出后经两小球在空中相遇。已知、 两点间的距离为
,忽略空气阻力,重力加速度取 。下列说法正确的是( )
BD
A.小球的出射速度大小为
B.小球的出射速度大小为
C.两小球相遇时小球 处于上升阶段
D.两小球相遇位置离点的水平距离大于离 点
的水平距离
【解析】 根据题意有 ,
,代入数据联立解得 ,
。
小球、出射时竖直方向的速度分别为 ,
,小球 上升到最高点经过的时间为
,所以两小球相遇时小球 处于下降阶段。
两小球相遇时的水平位移分别为, ,
,即两小球相遇位置离点的水平距离大于离 点的水平距离。
专题四 曲线运动
考向一 抛体运动
2025年高考物理专题复习资料
考点切片
考点1 运动的合成与分解
题组1 合运动与分运动
1.(2024安徽安师大附中模拟)如图所示,夜晚一同学拿一手电筒水平照向一倾斜的墙
壁,墙壁与水平面成 角,当该同学沿垂直于光束方向以大小为 的竖直速度运动时,
光斑以速度 沿墙壁向上运动,关于墙壁上的光斑的运动情况,下列说法正确的是
( )
B
A.光斑做匀加速直线运动
B.光斑做匀速运动,运动的速度大小大于
C.光斑做匀速运动,运动的速度大小等于
D.光斑做匀减速直线运动
【解析】 光斑的运动为合运动,其速度的竖直分量等于手电筒的运动速度,根据
运动的合成与分解知识可知,解得光斑的速度 ,故光斑做匀速运动,
运动的速度大于 。
2.(2023江苏卷)达·芬奇的手稿中描述了这样一个实验:使一个罐子在空中沿水平直线
向右做匀加速运动,沿途连续漏出沙子。若不计空气阻力,则下列图中能反映空中沙子
排列的几何图形是( )
D
A. B. C. D.
【解析】
题组2 小船过河问题
解题觉醒
1.题型特征:求解小船过河的最短时间、最短位移问题。
2.解题技巧
(1)如果要以最短时间过河,让船速方向与河岸垂直,设河宽为
(2)如果要以最短位移过河。第一步:求
角,
移,过河时间
3.[多选](2025山东烟台阶段练习)随着强降雨季节的临近,各地开展“防溺水、强
救援”应急演练活动。如图所示,在某段平直河流的中心有遇险人员 (随水流向下游漂
移)等待救援,救援人员在岸边点( 垂直河岸)驾驶冲锋舟以最短时间救上遇险人
员 后,冲锋舟实时调整航向以最短距离回到岸边。已知冲锋舟在静水中的速度
,河中某处水流速度大小与到岸边距离 成正比,水流方向与河岸平行,
已知河中央水流速度为,到岸边的距离为 。下列说法正确的是( )
BC
A.前往河中央的过程中,冲锋舟的运动轨迹为直线
B.从岸边到达救援地点最少需要
C.从救援地点返回的过程中,冲锋舟行驶的路程为
D.返回岸边时,冲锋舟的速度大小为
【解析】 冲锋舟前往救援地点过程中,要求时间最短,需要船头垂直河岸,冲锋
舟在水中参与了一个匀速直线运动和一个匀变速直线运动(【点拨】由题意可得前往河
中央的过程中,有,其中 为常量,可知在平行河岸方向上冲锋舟做匀
加速直线运动。),故合运动轨迹为曲线。
从岸边到达救援地点需要的最短时间 。
从救援地点返回过程中,要求位移最短,由于冲锋舟在静水中速度大于水流速度
(【点拨】由题意可知冲锋舟在静水中的速度大于河中央水流速度,因此返回过程中冲
锋舟在静水中速度始终大于水流速度),冲锋舟在静水中速度沿河岸方向的分速度可以
和水流速度抵消,故冲锋舟的实际速度可以始终垂直于河岸,因此最短位移为
(【大招运用】根据大招内容中口诀“船快取河宽,水快除以余弦”,返回过程中冲锋舟
在静水中速度始终大于水流速度,则最短位移为 。)。
. .
冲锋舟回到岸边时,水流速度为零,冲锋舟速度大小为其在静水中的速度 。
4.[多选](2024黑龙江哈师大附中月考)如图所示,甲、乙两船在同一条河流中同时
开始渡河,河宽为,、分别是甲、乙两船的出发点,两船头与河岸均成 角,甲
船船头恰好对准点的正对岸点,经过一段时间乙船恰好到达 点。如果两船在静水中
速度大小均为 ,且两船相遇不影响各自的航行,下列判断正确的是( )
AD
A.水流方向向右,速度大小为
B.甲船沿河岸方向位移大小为
C.甲、乙两船不会在 上某点相遇
D.两船同时到达河对岸,花费时间均为
【解析】 由于乙船恰好到达 点,则可知水流方向向右,且乙船沿河岸方向的分
速度大小恰好等于水流的速度大小,即 。
甲、乙两船在垂直于河岸方向的分速度均为 ,因此到达对岸的时间均
为,甲船沿河岸方向位移大小 ,联立解得
。
由于乙船沿运动,甲船船头恰好对准点的正对岸 点(【点拨】甲船在静水中
的运动方向由指向。),在水流的作用下,甲船到达对岸时,应在 点的右侧,而
两船在垂直于河岸方向速度相同,一定会相遇,且在 上某点相遇(【点拨】乙船实
际运动为沿着虚线到达对岸点,则两船相遇点一定在 上。)。
. .
. .
跳跳学长有话说
本题也可运用作图法求解,甲、乙两船的分运动与合运动构成的平行四边形如图所示。
两船相对河岸的运动(实际运动)为合运动,分别相对静水的运动及沿水流方向的运动
为分运动。
题组3 关联速度问题
解题觉醒
1.题型特征:用绳、杆等连接的两物体,求解关联物体的速度。
2.解题步骤
(1)画出绳、杆等两端的实际速度;
(2)将两端的实际速度分别沿绳(或杆)方向和垂直于绳(或杆)方向正交分解;
(3)利用两物体沿绳(或杆)方向速度大小相等,求实际速度大小关系。
5.(2025江苏前黄高级中学开学考)影视作品中的武林高手展示轻功时都是吊威亚
(钢丝)的。如图所示,轨道车通过细钢丝跨过滑轮拉着特技演员 上升,便可呈现
出演员飞檐走壁的效果。轨道车沿水平地面以速度大小 向左匀速前进,某
时刻连接轨道车的钢丝与水平方向的夹角 为 ,连接特技演员 的钢丝竖直,取
, ,则下列说法正确的是( )
A
A.该时刻特技演员 有竖直向上的加速度
B.该时刻特技演员 处于失重状态
C.该时刻特技演员的速度大小为
D.该时刻特技演员的速度大小为
【解析】 将车速 沿着细钢丝方向和垂直于细钢丝的方向分解,沿着细钢丝
方向的分速度与特技演员的速度大小相等,即 ,其中车速 不变,
随着小车向左运动, 不断减小,则不断增大,即特技演员 有竖直向上的加速度,
处于超重状态。
当 时,特技演员的速度大小为 。
6.[多选](2024广东深圳中学检测)如图所示,有一个水平向
左做匀速直线运动的半圆柱体,速度为 ,半圆柱体上有一根能
沿竖直方向运动的竖直杆,在竖直杆未下降到地面之前,杆同半
圆柱体接触点和柱心的连线与竖直方向的夹角为 ,杆的速度
为 ,下列说法正确的是( )
AD
A.竖直杆向下做加速直线运动 B.竖直杆向下做减速直线运动
C. D.
【解析】 设杆受半圆柱体的弹力为 ,将半圆柱体和杆的
速度分别沿弹力 所在的直线方向与杆同半圆柱体
接触点的切线方向分解,如图所示。 因为两接触运动物体沿接触弹
力方向的分速度大小相等(【点拨】所谓接触就是在接触面的垂线
方向二者没有相对运动,你走多少我走多少,否则就要分开,所以
在接触面的垂线方向分速度大小相等。),所以有
,则 ,杆向下运动, 变大, 变大, 变大,
杆做加速直线运动。
根据 ,得 。
7.(2024河南郑州第十一中学月考)如图所示,一根长直轻杆两端
分别固定小球和 ,竖直放置,两球半径忽略不计。由于微小的
扰动,球沿竖直光滑槽向下运动, 球沿水平光滑槽向右运动,
当杆与竖直方向的夹角为 时(图中未标出),关于两球速度
与 的关系正确的是( )
C
A. B. C. D.
【解析】 当杆与竖直方向的夹角为 时,将两小球的实际
速度沿杆方向和垂直于杆方向正交分解,如图所示,沿杆方
向两分速度大小相等,则 , ,
C正确。
考点2 平抛运动
题组1 平抛运动的基本规律
8.[多选](2025河北承德部分学校摸底)两位同学做平抛实验时,一
位同学将一小球水平抛出,另一位同学进行频闪照相,闪光频率为 。
已知小球在抛出瞬间闪光灯恰好闪光,如图所示, 为小球抛出瞬间的影
像,和之间、和之间均有1个影像未画出, 连线与水平方向的夹
角为 ,重力加速度取 ,不计空气阻力。下列说法正确的是
( )
AC
A.线段的长度为 B.小球的初速度大小为
C.线段的长度为 D.对应时的小球速度大小为
【解析】
解题第2季武林大会
分析平抛运动时,也可以利用数学方法,联立平抛运动方程、 ,得到
这个不含的平抛轨迹方程,代入轨迹上点的坐标,直接求出初速度 。
——广东湛江一中 王舶蘅
9.[多选](2023天津一中月考)投壶是从
先秦延续至清末的中国传统礼仪和宴饮游戏,
《礼记传》中提到:“投壶,射之细也。燕
饮有射以乐宾,以习容而讲艺也。”如图甲
BD
A.、两人所投箭的初速度大小之比为
B.、两人所投箭落入壶口时的速度大小之比为
C.、两人投射位置与壶口的水平距离之比为
D.、两人投射位置与壶口的水平距离之比为
所示,、 两人在不同位置沿水平方向各投出一支箭,如图乙、丙所示,箭尖插入壶
中时与水平面的夹角分别为 和 。已知两支箭质量相同,竖直方向下落的高度相
等。忽略空气阻力、箭长、壶口大小等因素的影响,下列说法正确的是
( )
【解析】 沿水平方向投出后,箭做平抛运动,两支箭竖直方向下落高度相等,则
两支箭在空中的运动时间相同(【点拨】箭在竖直方向上做自由落体运动,有
。 ),下落到瓶口时竖直方向上的速度相同,设箭尖插入壶中时与水平面的夹
角为, 箭投出时的初速度为,则,即 ,两支箭投出的初速度大
小之比为 。
设箭尖插入壶中时的速度大小为,则,即 ,两支箭落入壶口
时的速度大小之比为 。
因两支箭在空中的运动时间相同,甲、乙两人投射位置与壶口的水平距离之
比即初速度大小之比,为 。
10.(2023新课标卷)将扁平的石子向水面快速抛出,石子可能会在水面上一跳一跳地
飞向远方,俗称“打水漂”。要使石子从水面跳起产生“水漂”效果,石子接触水面时的速度
方向与水面的夹角不能大于 。为了观察到“水漂”,一同学将一石子从距水面高度为
处水平抛出,抛出速度的最小值为多少 (不计石子在空中飞行时的空气阻力,重力加
速度大小为 )
【答案】
【解析】 由题意可知石子接触水面前的运动可理想化为平抛运动,则其在竖直方向做
匀加速直线运动。从距水面高度为处水平抛出石子,由 可得,落到水面时其
竖直方向的速度为
要使石子落水时的速度方向与水面的夹角不大于 ,则
解得,即抛出速度的最小值 。
题组2 平抛运动的重要推论
解题觉醒
1.题型特征:题目中出现速度偏转角
夹角、速度反向延长线等关键词。
2.解题技巧
(1)
(2)速度反向延长线过水平位移中点。
11.(2025江苏南通阶段练习)如图所示,一小球从某高度处水平
抛出,经过时间到达地面时,速度与水平方向的夹角为 ,不计
空气阻力,重力加速度为 。下列说法正确的是( )
A
A.小球水平抛出时的初速度大小为
B.小球在时间内的位移与水平方向的夹角为
C.若小球初速度增大,则平抛运动的时间变长
D.若小球初速度增大,则 增大
【解析】 小球落地时竖直方向上的分速度为 ,因为落地时速度方向与水平
方向的夹角为 ,所以小球的初速度为 。
小球落地时速度方向与水平方向夹角的正切值 ,位移与水平方向夹角的
正切值,所以,但 (【大招运用】根据大招内容
中平抛运动的推论可知速度偏转角 的正切值等于位移偏转角 的正切值的2倍,可得
。)。
根据,解得 ,可知小球运动时间与下落高度有关,与初速度无关,
若小球初速度增大,则平抛运动的时间不变。
. .
小球落地时速度方向与水平方向夹角的正切值为 ,若小球初速度增大,
下落时间不变,则 将减小,即 减小。
12.(2025江苏淮安开学考)如图所示,半球面的半径为,球面上点与球心 等高,
小球先后两次从点以不同的速度、沿方向抛出,下落相同高度 ,分别撞击到
球面上、点。设上述两过程中小球运动时间分别为、 ,速度的变化量分别为
、 。则( )
C
A. B.
C.,式中为重力加速度 D.撞击 点时的速度方向与球面垂直
【解析】 小球两次均做平抛运动且下落高度相同,根据 可知,运动时间
相同。
根据 ,由于运动时间相同,所以速度变化量也相同。
设小球两次运动的水平位移分别为和,由几何关系可知 ,
,根据平抛运动规律,可知,,又有 ,联
立可得 。
若小球撞击点时的速度方向与球面垂直,则点速度方向的反向延长线过圆心 ,
根据平抛运动的推论,速度的反向延长线一定过水平位移的中点,而 点不是水平位移
的中点,与假设相矛盾,所以小球撞击 点时的速度方向与球面不垂直。
13.(2025重庆南开中学开学考)如图所示,一个质量为 的小球
从倾角为 的斜面顶端以速度水平向右抛出,重力加速度为 ,
斜面足够长,不计空气阻力,下列说法正确的是( )
D
A.从抛出小球开始计时,经过 后小球距离斜面最远
B.小球抛出的初速度越大,则小球落到斜面上的速度方向与水平
方向的夹角也越大
C.若小球还受到一个竖直向下的恒力,恒力大小与其重力大小相
等,则小球落到斜面上的速度大小为
D.若小球还受到一个位于竖直平面内的恒力(方向未知),且小
球抛出经过足够长的时间之后速度方向趋于与斜面平行,则该恒
力的最小值是
图1
【解析】 如图1所示,小球距离斜面最远时速度方向
与斜面平行(【点拨】将小球的速度沿平行斜面方向和垂
直斜面方向分解当小球垂直斜面方向的分速度为0时,小球
距离斜面最远,此时小球速度方向与斜面平行。),可得
,即 。
在平抛运动中,速度偏转角的正切值是位移偏转角正
切值的两倍。由于小球在斜面上抛出又落在斜面上,因此
在以不同初速度抛出的情况下位移偏转角相同,则速度偏转角相同。故增大初速度,速
度偏转角不变。
图2
若小球还受到一个竖直向下的恒力,恒力大小与其重
力大小相等,由牛顿第二定律可得 ,
则小球的加速度 ,分解小球落在斜面上的速度,如
图2所示,可得 ,
。
图3
如图3所示,经过足够长的时间,小球的速度趋于与斜
面平行,则合力的方向与斜面方向平行。由几何关系可知,
当恒力方向与合力方向垂直时,恒力最小,恒力的最小值
为 。
题组3 平抛运动的轨迹比较问题
解题觉醒
1.题型特征:给出两个平抛轨迹,比较物体的初速度和落地时间。
2.解题技巧:口诀“高度大时间长,同起点大压小,起点不同先平移”。
14.(2024重庆调研)甲、乙两球位于同一竖直线上的不同
位置,甲比乙高,如图所示,将甲、乙两球分别以、
的速度沿同一方向水平抛出,不计空气阻力,下列条件中
有可能使乙球击中甲球的是( )
D
A.同时抛出,且 B.甲比乙后抛出,且
C.甲比乙早抛出,且 D.甲比乙早抛出,且
【解析】 题图中,乙球击中甲球的条件是:水平位移相等,甲球竖直位移等于乙
球的竖直位移加上,甲球应先抛出,故有, ,联立解得
, 。
跳跳学长传妙招
应用大招口诀“高度大时间长”,可知甲的高度大,所需时间较长,若让两球相撞,则甲
要先抛出。将甲球轨迹向下平移至甲、乙两球的抛出点在同一点,如图中轨迹③所示。
根据“同起点大压小,起点不同先平移”,可知 。
15.(2024福建厦门一中检测)如图所示,轴在水平地面上, 轴沿竖直方向,图中画
出了从轴上沿轴正方向抛出的三个小球、和的运动轨迹,其中和 是从同一点抛
出的,不计空气阻力,则( )
B
A.的运动时间比的长 B.和 的运动时间相同
C.的初速度与的初速度可能相等 D.的初速度比 的小
【解析】 三个小球在竖直方向都做自由落体运动,根据 ,得
,比抛出时的高度低,则比运动的时间短;、抛出的高度相同,则和
运动的时间相同。
比运动的时间短,的水平位移大于的水平位移,则的初速度大于 的初速度。
、的运动时间相等,的水平位移大于的水平位移,则的初速度大于 的初速
度。
跳跳学长有话说
根据大招口诀“高度大时间长”,可知、的高度一样且大于的高度,则、 下落时间
相等,且大于的下落时间,A错误,B正确;将球轨迹向下平移至、 两球的抛出点
在同一点,如图中轨迹 所示。根据“同起点大压小,起点不同先平移”,可知
,C、D错误。
题组4 斜面平抛比例问题
16.(2024广西南宁期末)滑雪是一项非常刺激且具观赏
性的运动项目。如图所示,运动员甲、乙(视为质点)
从水平跳台向左分别以初速度和 水平飞出,最后都
落在着陆坡(可视为斜面)上,不计空气阻力,则运动
员从水平跳台飞出到落在着陆坡上的过程中,下列说法
正确的是( )
D
A.飞行的时间之比 B.水平位移之比
C.落到坡面上的瞬时速度大小相等 D.落到坡面上的瞬时速度方向相同
【解析】 设斜坡倾角为 ,则有,解得 ,
可知他们飞行时间之比为(【大招运用】根据大招内容中的口诀“之比
不变,只有位移要方”,由题意可知、水平位移之比 。)。
根据,可得他们飞行的水平位移之比为 。
根据平抛运动的推论:瞬时速度与水平方向夹角的正切值是位移与水平方向
夹角正切值的两倍,只要是落在坡面上,位移与水平方向夹角相同,所以两人落到坡面
上的瞬时速度方向一定相同,故落在坡面上的瞬时速度大小之比等于初速度大小之比,
为 。
. .
17.[多选](2024山西大同模拟)如图所示,质量相同的两小
球、分别从斜面顶端和斜面中点 沿水平方向抛出后,恰好
都落在斜面底端,不计空气阻力,下列说法正确的是( )
ACD
A.小球、在空中飞行的时间之比为
B.小球、抛出时的初速度大小之比为
C.小球、到达它们与斜面距离最大位置时的速度大小之比为
D.小球、到达斜面底端时速度大小之比为
【解析】 因为、两球下落的高度之比为,根据得 ,则飞行
的时间(【点拨】飞行时间仅由下落的高度决定。)之比为 。
、两球的水平位移之比为,运动时间之比为,根据 知,初速度大
小之比为 。
设斜面的倾角为 ,小球、到达它们与斜面距离最大位置时的速度为
(【点拨】此时小球速度方向与斜面方向平行。将小球速度沿水平方向和竖直方向进行
分解,即可得出此时小球速度与初速度的关系。),与初速度成正比,则小球、 到
达它们与斜面距离最大位置时的速度大小之比为 。
. .
小球落在斜面上时,速度方向与水平方向夹角的正切值是位移与水平方向夹角正
切值的2倍,因两小球都落在斜面上,故两小球的位移与水平方向的夹角相等,则两小
球到达斜面底端时的速度方向与水平方向的夹角也相等(【点拔】 “速度角”
“位移角”=“斜面角),设该夹角为 ,则 ,末速度大小与初速
度大小成正比,即小球、到达斜面底端时的速度大小之比为 。
题组5 平抛运动的临界问题
18.[多选](2024山西运城康杰中学检测)康杰中学举办的“学雷锋集爱
心”义卖活动中,有班级设置了套圈游戏,如图所示。某同学从距水平地
面高度处水平抛出一个半径为 的圆环,套前方地面上的水杯,
假设圆环运动过程中始终保持水平,圆环中心到水杯的水平距离为 ,
水杯高度为,水杯大小忽略不计。取 ,忽略空气阻力,要
想套住水杯,圆环刚抛出时的速度可以是( )
AB
A. B. C. D.
【解析】 已知圆环抛出时的高度,圆环的半径为 ,水杯的高度为
,圆环中心到水杯的水平距离为 ,根据平抛运动规律可知
,解得 ,(【点拨】无论圆环抛出时速度大小如何,圆环下落
高度一定,下落时间一定。)当圆环右侧贴着水杯落下时,圆环抛出时的初速度有最小
值,即,解得 ;当圆环左侧贴着水杯落下时,圆环抛出时的初
速度有最大值,即,解得 ,要使圆环套住地面上的水杯,圆环
刚抛出时的速度应该满足,故选 。
. .
. .
19.(2025辽宁鞍山一模)如图甲为一个网球场的示意图,一个网球发球机固定在边角
处,可以将网球沿平行于地面的各个方向发出,发球点距地面高度为,球网高 。
图乙为对应的俯视图,其中, 。按照规则,网球发出后不触网且落
在对面阴影区域(包含虚线)内为有效发球。图中虚线为球场的等分线,则发球机有效
发球时发出网球的最小速率为(忽略一切阻力,取 )( )
A
A. B. C. D.
【解析】 第一步:构建运动模型——平抛运动。
当发球机有效发球且发出网球的速率最小时,球应恰好到达有效区域的边缘,如答图所
示,设网球从点发出后落在 点。
第二步:化曲为直——即分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
网球从点发出后,在竖直方向做自由落体运动,有,解得 ,网球
恰不触网(【点拨】根据大招内容中的平抛轨迹比较口诀“高度大时间长,同起点大压
小,起点不同先平移”可知,发出网球的速率最小时,网球的运动轨迹应在最下边,因
此此情况下网球恰不触网。),则有,解得 ,网球在水平方向
上做匀速直线运动,则,因与 为相似三角形,则有
,因,,可得 ,
。
第三步:由水平方向的分运动求网球的最小速
率。
则发球机有效发球时发出网球的最小速率为
,A正确。
考点3 抛体运动的关联运动
20.[多选](2024黑龙江哈师大附中期中)如图所示,同一竖直平面内有四分之一圆
弧和倾角为 的斜面,、两点与圆弧的圆心 等高。现将甲、乙两小球分
别从、两点以初速度、沿水平方向同时抛出,两球恰好在 点相碰(不计空气阻
力),已知, 。下列说法正确的是( )
AD
A.初速度、大小之比为
B.若仅增大 ,则两球不再相碰
C.若大小变为原来的一半,则甲球恰能落在斜面的中点
D.若只抛出甲球并适当改变初速度大小,则甲球可能垂直击中
圆环
【解析】 设圆弧所在圆的半径为,甲、乙两球从等高处做平抛运动恰好在
点相碰,则运动时间相等,水平方向有, ,所以
。
【点拨】在 点相碰,说明两球的下落高度相等,则运动时间相等。
两球相碰,则满足,因两球始终在同一水平面上,故若仅增大 ,
显然存在 满足方程,两球会相碰。
若 大小变为原来的一半,在时间不变的情况下水平位移会变为原来的一半,但由
于甲球会碰到斜面,下落高度减小,时间减小,所以甲球的水平位移小于原来的一半,
不会落在斜面的中点。
如图所示,若甲球以速度水平抛出,垂直击中圆弧 ,则
落点速度的反向延长线过圆心 ,由几何关系有
, (【点拨】平
抛运动的解题规律就是位移分解方程和速度分解方程。),以上
两个方程有两个未知
数,可以求解和 ,因此只抛出甲球并适当改变初速度大小,甲球可能垂直击中圆弧
。
. .
21.(2024云南大理模拟)如图所示,将小球从点以速度水平抛出,同时将小球
从水平地面上的点以速度竖直上抛,、两个小球在同一竖直平面内运动,且在
点正上方的某一位置相遇。已知点到水平地面的高度为,、 两点的水平距离为
,、 两个小球可视为质点,空气阻力可忽略不计。则下列说法正确的是( )
C
A.、两个小球相遇时,小球 一定处于上升过程中
B.只改变小球的水平速度,、两个小球依旧能在 点
正上方相遇
C.、两个小球初速度必须满足
D.、 两个小球从抛出到相遇的过程中,两球的速度变化
量不相等
【解析】 小球做平抛运动,,若与相遇时下落的高度为,则 ,
小球做竖直上抛运动,,联立以上式子可得 。
、两个小球在上升、下降过程中或 到达最高点时均有可能相遇。
若只改变小球的水平速度,不再满足,、两个小球不可能在 点正上
方相遇。
、两个小球从抛出到相遇过程中,加速度均为重力加速度,运动时间 相等,
故速度的变化量 也相同。
考点4 类平抛运动
22.[多选](2024江西吉安白鹭洲中学模拟)一足够大且光滑的矩形斜面,倾角为 ,
高为,现有一小球在处沿平行于底边的初速度滑上斜面,最后从 处离开斜面。已
知重力加速度大小为 。下列说法正确的是( )
ABC
A.小球的运动轨迹为抛物线
B.小球的加速度大小为
C.小球从处到达处所用的时间为
D.小球从处到达处的位移大小为
【解析】 小球受重力和支持力两个力,合力沿斜面向下,与初速度方向垂直,小
球做类平抛运动,其运动轨迹为抛物线。
根据牛顿第二定律,有,解得 。
由几何关系得,小球沿加速度方向上的位移为,根据位移公式 ,
解得 。
小球在沿初速度方向的位移为,则小球从处到达 处的位移大
小为 。
23.(2025湖北新高考联考协作体开学考)如图所示,一物体在某液体中运动时只受到重
力和恒定的浮力的作用,且。如果物体从点以水平初速度 开始运动,最后
落在点,、间的竖直高度为,与右壁水平间距为,重力加速度为 ,则下列说
法正确的是( )
D
A.从运动到的时间为
B.与之间的水平距离为
C.若增大初速度 ,物体将可能撞击右壁,且初速度越大,物体
撞击右壁时的速度越大
D.若足够大,当初速度 时,物体撞击右壁时的速度最
小
【解析】 根据牛顿第二定律有,解得 ,该物体做类平抛运动,
则,解得物体从运动到的时间为 。
与之间的水平距离 。
根据大招内容中的平抛轨迹比较口诀“高度大时间长,同起点大压小,起点不
同先平移”可知,若增大初速度 ,物体将可能撞击右壁。物体撞击右壁时,物体运动
的时间为,物体在竖直方向的速度为 ,物体撞击右壁时的速度
,根据数学知识可知,当,即当初速度 时,
物体撞击右壁时的速度最小,故若增大初速度 ,物体将可能撞击右壁,撞击右壁时的
速度不一定越大。
跳跳学长敲黑板
有时物体的运动与平抛运动很相似,也是在某方向做匀速直线运动,在与之垂直的方向
做初速度为零的匀加速直线运动。这种运动,像平抛又不是平抛,通常称为类平抛运动。
处理方法与处理平抛运动方法一样,只是加速度 不同而已。
考点5 斜抛运动
24.(2023湖南卷)如图甲所示,我国某些农村地区人们用手抛撒谷粒进行水稻播种。某
次抛出的谷粒中有两颗的运动轨迹如图乙所示,其轨迹在同一竖直平面内,抛出点均为
,且轨迹交于点,抛出时谷粒1和谷粒2的初速度分别为和,其中方向水平, 方向
斜向上。忽略空气阻力,关于两谷粒在空中的运动,下列说法正确的是( )
B
图甲
图乙
A.谷粒1的加速度小于谷粒2的加速度 B.谷粒2在最高点的速度小于
C.两谷粒从到的运动时间相等 D.两谷粒从到 的平均速度相等
【解析】
只受重力→两谷粒加速度 ,A(×)
从到位移相同→谷粒2先上升后下降,用时更长,即 (×)
从到 位移相同
谷粒2在最高点只有水平速度
(【点拨】做斜抛运动的物体运动到最高点时其竖直方向速度为零。)
竖直方向
水平方向
谷粒合位移,
25.(2025陕西渭南阶段练习)如图所示,网球运动员训练时,运动员在同一高度的前
后两个不同位置、将网球斜向上击出后,网球恰好垂直击中竖直墙上的同一固定点 。
已知网球从运动到的时间为,重力加速度大小为 ,忽略空气阻力,下列说法正确
的是( )
C
A.从点击出的网球比从 点击出的网球的初速度小
B.若、两点间的距离为,则在、 两点的击球速度大
小之差为
C.在 点将网球击出时,若网球的速度方向与竖直方向的
夹角为 ,则点与墙面间的距离为
D.若、两点间的距离与、两点间的距离之比为 ,
则从、两点击出的网球的速度大小之比也为
【解析】 采用逆向思维,网球做平抛运动,根据 ,两【点拨】分析科抛
运动,只有物体运动到最高点,才能利用逆向思维将物体的运动看成反方向的平抛运动。
次高度相同,故网球在、两点时竖直方向的速度相同,根据,可得 ,
可知两球运动时间相同,而以轨迹1运动的水平位移大,在水平方向上,根据 可
知以轨迹1运动的水平速度比以轨迹2运动的水平速度大,根据可知从 点
击出的网球的初速度比从 点击出的网球的大。
采用逆向思维,网球做平抛运动,两球运动的时间相等,均为 ,在水平方向上有
,解得水平方向速度大小之差为 ,但在
、两点的击球速度在竖直方向有分量,故 。
采用逆向思维,网球做平抛运动,竖直方向的高度为 ,根据速度偏转角正
切值等于位移偏转角正切值的两倍,有 (【提醒】注意网球的速度方向与竖
直方向的夹角为0.而不是与水平方向的夹角为 。),解得 点与墙面间的距离为
。
若、两点间的距离与、两点间的距离之比为 ,两球运动时间相等,根据
平均速度的定义可知,从、 两点击出的网球在整个运动过程中的平均速度大小之比
也为 。
26.[多选](2025山东齐鲁名校联盟开学考)如图所示,从同一水平面上的、 两点
同时抛出两个小球、,出射速度与水平方向夹角分别为 和 ,两小球运动轨
迹在同一竖直面内,射出后经两小球在空中相遇。已知、 两点间的距离为
,忽略空气阻力,重力加速度取 。下列说法正确的是( )
BD
A.小球的出射速度大小为
B.小球的出射速度大小为
C.两小球相遇时小球 处于上升阶段
D.两小球相遇位置离点的水平距离大于离 点
的水平距离
【解析】 根据题意有 ,
,代入数据联立解得 ,
。
小球、出射时竖直方向的速度分别为 ,
,小球 上升到最高点经过的时间为
,所以两小球相遇时小球 处于下降阶段。
两小球相遇时的水平位移分别为, ,
,即两小球相遇位置离点的水平距离大于离 点的水平距离。
同课章节目录
