考向二 圆周运动-2025年高考物理专题复习课件
文档属性
| 名称 | 考向二 圆周运动-2025年高考物理专题复习课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-02-18 00:00:00 | ||
图片预览










文档简介
(共90张PPT)
专题四 曲线运动
考向二 圆周运动
2025年高考物理专题复习资料
考点切片
考点1 描述圆周运动的物理量
1.[多选](2025广西名校联合调研)有一种很火的益智玩具——“磁悬浮
陀螺”,依靠磁场力可以让旋转的陀螺悬浮在空中,如图所示。对处于悬
浮状态的陀螺,下列说法正确的是( )
AD
A.距离陀螺中心越远的点,线速度越大
B.陀螺上各点均处于平衡状态
C.陀螺处于完全失重状态
D.若陀螺绕其中心的转速为,则陀螺上距离中心处质点的向心加速度大小为
【解析】 “磁悬浮陀螺”各点的角速度相同,距离中心越远的点,转动半径越大,
线速度越大。
陀螺上各点做圆周运动,是曲线运动,所以各点不处于平衡状态。
陀螺悬浮在空中,陀螺在竖直方向上受力平衡,既不超重也不失重。
质点的角速度为,向心加速度大小为 。
2.(2025江苏南通阶段练习)、 两艘快艇在湖面上做匀速圆周运动(如图所示),在
相同时间内,它们通过的路程之比是,运动方向改变的角度之比是 ,则它们
( )
A
A.线速度大小之比为 B.角速度大小之比为
C.圆周运动的半径之比为 D.向心加速度大小之比为
【解析】 因为相同时间内快艇通过的路程之比是,根据可得、 的线速
度大小之比为 。
相同时间内快艇运动方向改变的角度之比为,根据 可得角速度大小之比
为 。
根据可得快艇做圆周运动的半径之比为 。
根据 可得快艇向心加速度大小之比为 。
考点2 圆周运动中的传动问题
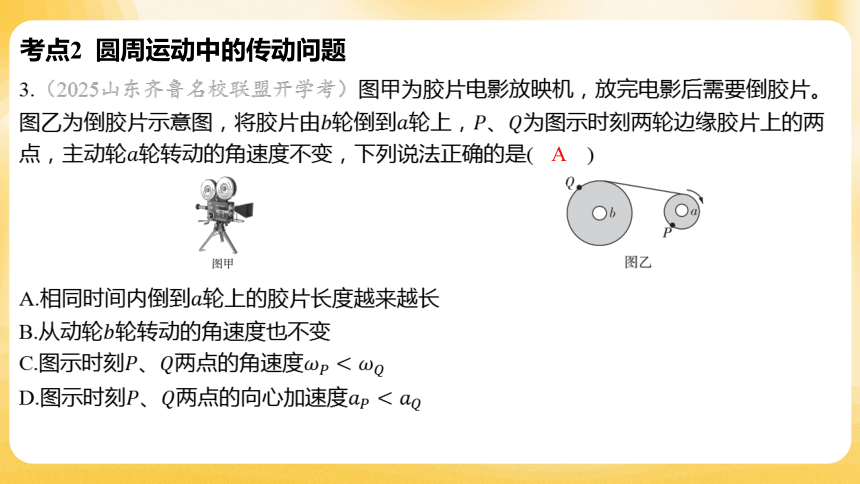
3.(2025山东齐鲁名校联盟开学考)图甲为胶片电影放映机,放完电影后需要倒胶片。
图乙为倒胶片示意图,将胶片由轮倒到轮上,、 为图示时刻两轮边缘胶片上的两
点,主动轮 轮转动的角速度不变,下列说法正确的是( )
A
A.相同时间内倒到 轮上的胶片长度越来越长
B.从动轮 轮转动的角速度也不变
C.图示时刻、两点的角速度
D.图示时刻、两点的向心加速度
【解析】 胶片由轮倒到轮上,则轮半径逐渐增大,主动轮 轮转动的角速度不
变,根据可知轮边缘的线速度增大,故相同时间内倒到 轮上的胶片长度越来越
长。
由题意可知、轮边缘的线速度始终相等,轮的半径减小,根据 可知从动
轮 轮转动的角速度增大。
题图图示时刻、两点的线速度相等,,根据可知 ,
根据向心加速度公式可知 。
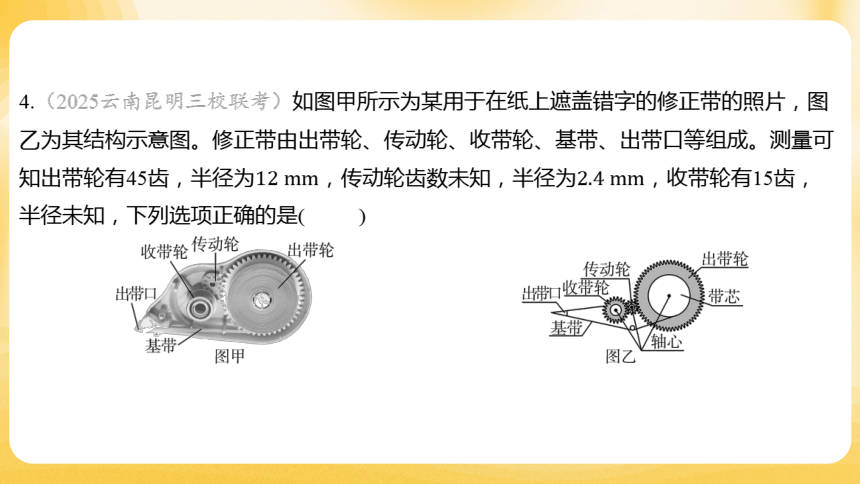
4.(2025云南昆明三校联考)如图甲所示为某用于在纸上遮盖错字的修正带的照片,图
乙为其结构示意图。修正带由出带轮、传动轮、收带轮、基带、出带口等组成。测量可
知出带轮有45齿,半径为,传动轮齿数未知,半径为 ,收带轮有15齿,
半径未知,下列选项正确的是( )
A.使用时,出带轮与收带轮转动方向相反
B.根据题中信息,可以算出传动轮的齿数
C.根据题中信息,不能算出收带轮轴心到齿轮边缘的半径
D.在纸面长时间匀速拉动修正带时,出带轮轴心上缠绕的带盘边缘某点的向心加速度大
小不变
√
【解析】 由于齿轮传动,根据题图乙可知,使用时,出带轮与传动轮转动方向相
反,传动轮与收带轮转动方向相反,则出带轮与收带轮转动方向相同。
由于是齿轮传动,相邻齿之间的间距相等,则有,解得 。
由于是齿轮传动,相邻齿之间的间距相等,则有,解得 ,
可知根据题中信息,能算出收带轮轴心到齿轮边缘的半径。
根据向心加速度的表达式有 ,在纸面长时间匀速拉动修正带时,出带轮轴心
上缠绕的带盘边缘某点所在的圆周半径减小,则向心加速度变大。
5.(2024四川成都外国语学校检测)如图为《天工开物》中记录的“牛转
翻车”,该设备利用畜力转动不同半径齿轮来改变水车的转速,从而将
水运送到高处。图中、 分别为两个齿轮边缘上的点,齿轮半径之比为
;、在同一齿轮上且、到转轴的距离之比为 ,
则在齿轮转动过程中( )
C
A.、的角速度相等 B.的线速度比 的线速度小
C.、的周期之比为 D.、的向心加速度大小之比为
【解析】 第一步:确定半径比。
第二步:确定不变量。
、齿轮传动,,、同轴转动, .
第三步:得出结论。
由和得, 。
由,得,又因, ,
,得, 。
考点3 水平面内圆周运动的3大模型
题组1 圆盘模型
大招27 对应练习
解题觉醒
1.题型特征:物体在转动的粗糙圆盘上随着圆盘做圆周运动,求摩擦力、何时滑动等问题。
2.解题技巧
图甲
(1)单物体圆盘:如图甲所示,直接列 ,求解物体不滑动时圆盘
最大的角速度。
图乙
①求绳子产生拉力时的角速度。列 。
②求两物体一起滑动时的角速度。先用质心法算出,再列 ,求解两物体不滑
动时圆盘最大的角速度。
(2)两物体圆盘:如图乙所示。
6.(2025江苏南通名校联盟调研)摩擦传动是传动装置中的一个重要模型,如图所示的
两个水平放置的轮盘靠摩擦力传动,其中、 分别为两轮盘的轴心,已知两个轮盘甲、
乙的半径比 ,且在正常工作时两轮盘不打滑。今在两轮盘上分别放置两个
由同种材料制成的滑块、,两滑块与轮盘间的动摩擦因数相同,两滑块距离轴心 、
的间距满足 。若轮盘乙由静止开始缓慢地转动起来,且转速逐渐增加,则下
列叙述正确的是( )
①滑块和 在与轮盘相对静止时,角速度之比
为
②滑块和 在与轮盘相对静止时,向心加速度
之比为
③轮盘乙转速增加后滑块 先发生滑动
④轮盘乙转速增加后滑块 先发生滑动
A.①②③ B.①②④ C.②③④ D.①③④
√
【解析】 摩擦传动的物体边缘线速度相等,则轮盘甲、乙边缘的线速度相等。、 与
轮盘相对静止时,分别和轮盘甲、乙做同轴转动,则、 做匀速圆周运动时,角速度
分别等于轮盘甲、乙的角速度。①根据 ,解得
,①正确;②根据可得滑块和 在与轮盘相
对静止时,向心加速度之比为,②正确;、 滑
块受到的摩擦力提供它们做圆周运动的向心力,则滑块恰好与轮盘发生相对滑动时有
,,解得 (【大招运用】根据大
招内容中滑块相对轮盘发生相对滑动的临界角速度,可得 。),
结合可知,转速增加后滑块 先发生滑动,③正确、④错误,故选A。
. .
. .
7.(2024重庆市实验中学模拟)如图甲所示,
两个完全相同的小木块和 (均可视为质
点)用轻绳连接置于水平圆盘上, 与转轴
的距离为 。圆盘从静止开始绕转轴极缓
慢地加速转动,木块和圆盘保持相对静止。
表示圆盘转动的角速度,、 与圆盘保
D
A.图线(1)对应 B.绳长为
C. D.时绳的拉力大小为
持相对静止的过程中所受摩擦力与满足如图乙所示关系,图中 。下列判断正
确的是( )
【解析】 第一步:当 时
对、分别分析:,,,、间绳没有拉力时, ,
图线1对应,图线2对应,由可知,解得 ,绳长
。
第二步:当 时绳子拉紧
对分析: ①
第三步:当时,、 整体开始滑动
对整体分析: ②
对分析:
联立①②解出 。
由题图乙可知,当时,绳上无拉力,木块和 都由各自所受的静摩擦
力提供向心力,,,因为,所以,故图线1对应 。
当时,木块所受的摩擦力恰好达到最大静摩擦力,且, ,
,即,可得,所以绳长为 。
当时,对木块,有,可得;当 时,
对木块,有,对木块,有 ,联立可得
(【大招运用】运用大招27可知 ,
。),所以, 。
. .
. .
. .
8.(2024江苏卷)陶瓷是以粘土为主要原料以及各种天然矿物经过
粉碎混炼、成型和煅烧制得的材料以及各种制品。如图所示是生
产陶瓷的简化工作台,当陶瓷匀速转动时,台面上掉有陶屑,陶
屑与台面间的动摩擦因数处处相等(台面足够大),最大静摩擦
力等于滑动摩擦力,则( )
D
A.离轴越远的陶屑质量越大 B.离轴 越近的陶屑质量越小
C.只有平台边缘有陶屑 D.离轴最远的陶屑距离不会超过某一值
【解析】 与台面相对静止的陶屑做匀速圆周运动,静摩擦力提供向心力,
当静摩擦力为最大静摩擦力时,根据牛顿第二定律可得,解得 ,因
与台面相对静止的这些陶屑的角速度相同,由此可知能与台面相对静止的陶屑离轴
的距离与陶屑质量无关,只要陶屑离轴的距离小于等于 ,陶屑在台面上均不发生
相对滑动,即只要在台面上不发生相对滑动的位置都有陶屑。
离轴 最远的陶屑受到的静摩擦力为最大静摩擦力时,由前述分析可知最大的运
动半径为, 与 均一定,故为定值,即离轴 最远的陶屑距离不超过某一
值。
题组2 圆锥摆模型
大招28 对应练习
解题觉醒
1.题型特征:绳子上端固定在天花板上,下端系着小球,小球在水平面上做匀速圆周运
动或小球在半球形碗(或倒锥桶)中做水平面内的圆周运动。
2.解题技巧
类型 示意图 结论
等长摆 _______________________________________ 更高、更快、更强(小球所处位置越高,线速度、角
速度和向心加速度均越大,向心力也越大)
类型 示意图 结论
等高摆 _____________________________________________ 不变
类型 示意图 结论
倒锥摆 ____________________________________________ 不变
9.[多选](2025福建厦门阶段练习)如图所示,质量为 的小球
用长为的细线悬于点,使小球在水平面内以角速度 做匀速圆
周运动。已知小球做圆周运动时圆心到悬点的距离为 。下列
说法正确的是( )
AC
A.细线对小球的拉力大小为
B.保持不变,增大角速度 ,细线与竖直方向的夹角变小
C.保持不变,增大细线长, 不变
D.保持不变,增大细线长 ,细线对小球拉力的大小不变
【解析】 设细线与竖直方向的夹角为 ,根据牛顿第二定律可得
, ,解得细线对小球的拉力大小为
,,由此可知,保持不变,增大角速度 ,细线与竖直方向的夹
角 变大(【大招运用】根据大招内容中的口诀“更高、更快、更强”,可知增大角速度
,细线与竖直方向的夹角 变大。)。
根据牛顿第二定律可得 ,解得,可知保持 不
变,增大细线长, 不变(【大招运用】根据大招内容可知等高摆的角速度 不
变。),根据 可知,细线对小球的拉力增大。
. .
. .
. .
. .
10.[多选](2025福建福州第一中学开学考)如图所示,两个同轴心的玻璃漏斗内表
面光滑,两漏斗与竖直转轴的夹角分别是 、 且 。、、 三个小球在漏斗
上做匀速圆周运动,、两球在同一漏斗的不同位置,球在另一个漏斗上且与 球位
置等高,下列说法正确的是( )
BC
A.球与球受到的支持力一定大小相等 B.球与 球的向心加速度一定大小相等
C.球与球的速度一定大小相等 D.球的周期一定等于 球的周期
【解析】 根据题意可知,球与 球均
做匀速圆周运动,合力提供向心力,分别对
两球受力分析,如图所示,由几何关系,对
球有,对球有,
由几何关系,对球有,对球有 ,根据
,可得球与球的向心加速度满足 (【大招运用】根据大招
内容可知倒锥摆中做匀速圆周运动的小球的加速度不变,可得 。)。
同理可知,球的向心力为,根据可知, 球做圆周运动
球与 球质量关系不确定,受到的支持力大小不一定相等。
. .
的速度为,同理可知,球做圆周运动的速度为,设球与 球距
离倒锥顶点的高度为(【易错】此处易错误地将球和 球看成等高摆。),由几何关
系可得 ,,可得,由公式 可知,由于
,则有 。
. .
. .
11.(2024辽宁大连期末)如图所示,一质量为的小球(可视为质点)由轻绳和 分
别系于一竖直细杆的点和点,、间的距离与两轻绳长度均为 。已知重力加速度
为,当小球随杆绕竖直轴以角速度 匀速转动时,下列说法正确的是( )
D
A.当时, 绳恰好没有拉力
B.当时,绳的拉力大小为
C.当绳有拉力时,总是比绳拉力小
D.当时,绳的拉力大小为
【解析】
时, 绳恰好 没有拉力 A( )
, 绳没有拉力 , ,解得 , B( )
绳有拉力时 , , 解得 C( )
, 绳 有拉力 , , 解得 D(√)
题组3 火车转弯模型
12.[多选](2024河南周口阶段练习)在修筑铁路时,弯道处的外轨会略高于内轨。
如图所示,当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时
的速度大小为,重力加速度为,两轨所在面的倾角为 ,则( )
ABD
A.该弯道的半径
B.当火车质量改变时,规定的行驶速度大小不变
C.当火车速率大于 时,内轨将受到轮缘的挤压
D.当火车速率小于 时,内轨将受到轮缘的挤压
【解析】 当火车以速率 转弯时,恰好由重力和支持力的合力提供向心力,
由牛顿第二定律可得,解得, ,该临界速度与火
车质量无关,故当火车质量改变时,规定的行驶速度大小不变。
当火车速率大于 时,重力与支持力的合力不足以提供向心力,火车有做离心运动
的趋势,故外轨将受到轮缘的挤压。
当火车速率小于 时,重力与支持力的合力大于所需的向心力,火车有做向心运动
的趋势,内轨将受到轮缘的挤压。
13.(2025广东汕头开学考)汽车的自动泊车系统持续发展,现有更先进的“全自动泊
车”。如图所示为某次电动汽车自动泊车全景示意图。汽车按图示路线(半径为的
圆弧与长为的直线构成)顺利停车,用时。汽车与地面间的动摩擦因数为
(最大静摩擦力等于滑动摩擦力),重力加速度取 ,汽车可视为质点,下列
说法正确的是( )
C
A.汽车在转弯过程中做匀变速曲线运动
B.汽车在转弯过程中的最大允许速度约为
C.汽车泊车的平均速度约为
D.汽车在泊车过程中受到的摩擦力总是与运动方向相反
【解析】 汽车在转弯过程中受到的摩擦力方向时刻变化,合外力方向也时刻变化,
所以汽车所做的运动不是匀变速曲线运动。
汽车转弯过程中靠静摩擦力提供向心力,又因为最大静摩擦力等于滑动摩擦力,
有,代入数据解得 。
汽车泊车过程的位移大小为 ,则汽车泊车的平均速
度约为 (【提醒】注意C选项要求的是平均速度,而不是
平均速率。)。
汽车在泊车过程中沿圆弧运动时所受摩擦力为提供向心力的静摩擦力和与运动方
向相反的摩擦力的合力,因此汽车在泊车过程中受到的摩擦力不总是与运动方向相反。
. .
. .
考点4 竖直面内圆周运动的3大模型
大招29 对应练习
解题觉醒
1.题型特征:物体在竖直平面内做圆周运动。
2.解题技巧
绳模型 杆模型 拱桥/凹形路面
最低 点 最高 点 速度较小时: 速度较大时:
绳模型 杆模型 拱桥/凹形路面
速度 最值 最高点最小速 度为 最高点最小速度为0 不脱离路面行驶的最大速度为
题组1 竖直圆绳模型
14.(2025山西大同一中月考)如图所示,竖直平面内的光滑圆轨道
半径为,、 点分别为轨道的最左侧、最高点。一小球在轨道内运
动且始终未离开轨道,重力加速度为 ,则( )
D
A.若小球运动到 点,小球在该位置所受的合力指向圆心
B.若小球运动到 点,小球在该位置的速度一定大于0
C.若小球运动到 点,小球在该位置一定受到轨道弹力
D.若小球运动到点,小球在该位置的速度一定大于等于
【解析】 若小球运动到 点,且小球在该位置受到的轨道弹力指向圆心,但重力
竖直向下,所以小球在该位置所受的合力不指向圆心。
若小球运动到 点,且小球在该位置的速度如果刚好等于0,则小球将在下半圆轨
道内来回运动,始终不会离开轨道。
若小球运动到 点,重力刚好提供向心力,则此时小球受到的轨道弹力刚好为
0,则有,可得,可知若小球运动到 点,在该位置的速度一定大
于等于 (【大招运用】根据大招内容可知绳模型中小球在最高点的最小速度为
。 )。
. .
. .
15.(2024江西南昌二中模拟)如图甲所示,小球用不可伸长的轻绳连接,绕定点 在竖
直面内做圆周运动,小球经过最高点时的速度大小为,此时轻绳拉力大小为 ,拉力
与速度的平方的关系如图乙所示,图像中的数据和以及重力加速度 都为已知量,
以下说法正确的是( )
C
A.数据 与小球的质量有关
B.数据 与小球的质量无关
C.比值 与小球的质量和圆周轨道半径都有关
D.利用数据、和 不能够求出小球的质量和圆周
轨道半径
【解析】 当时,轻绳的拉力为零,小球的重力提供向心力,设轻绳长为 ,
则有,解得,即,故数据 与小球的质量无关。
当时,对小球受力分析,有,解得,故数据 与小球
的质量有关。
根据以上分析可知,比值与小球的质量和圆周轨道半径(即轻绳长 )都有
关。
由以上分析可得, 。
跳跳学长 有话说
小球在拉力作用下通过最高点时,重力与拉力的合力提供向心力,
,运用图像的斜率和纵截距可知, ,
,则, ,A、B、D错误,C正确。
16.(2025山西吕梁阶段练习)如图所示,质量为的小物块用长为的细线悬挂于 点,
给物块一个水平初速度使其在竖直面内做圆周运动,物块运动到最低点时,细线的拉力
大小等于。斜面体固定在水平地面上,斜面长为,倾角为 , 竖直
且长也为。若物块做圆周运动到最低点时细线突然断开,此后物块恰好从 点无碰撞
地滑上斜面,最终落在地面上,物块与斜面间的动摩擦因数为,重力加速度为 ,
空气阻力不计,求:
(1) 小物块做圆周运动在最低点时的速度大小;
【答案】
【解析】 设物块运动到最低点时速度为,根据牛顿第二定律有
解得 。
(2) 小物块在斜面上运动的时间;
【答案】
【解析】 设物块运动到点时速度大小为 ,根据几何关系有
由于 ,因此物块在斜面上做匀速直线运动,在斜面上运动的时间
为 。
(3) 有斜面体时小球的落地点与无斜面体时小球的落地点间的距离。
【答案】
【解析】 物块运动到点时竖直方向的分速度
圆周运动的最低点与点的高度差
点离水平地面的高度
没有斜面体时,物块做平抛运动的水平位移
有斜面体时,物块做平抛运动下降高度,所经过的水平位移
. .
物块落地点离圆周运动最低点间的水平距离 (【点拨】
物块在斜面上做匀速直线运动,因此物块运动到点时的速度和物块到达 点时的速度
相等,物块运动到点后刚好“接着”物块到达 点时的运动继续做抛体运动,可将两个
运动过程合在一起等效为一个完整的平抛运动过程。)
则有斜面体时物块的落地点与无斜面体时物块的落地点间的距离为
。
. .
题组2 竖直圆杆模型
17.(2024陕西西安期中)如图所示,轻杆长为 ,在杆两端分别固
定质量均为的小球和,光滑水平转轴穿过杆上距小球为 处的
点。外界给系统一定能量后,杆和小球在竖直平面内转动,小球
运动到最高点时,杆对小球 恰好无作用力,忽略空气阻力,重力加
速度为。则小球 在最高点时( )
C
A.小球的速度为零 B.小球的速度大小为
C.水平转轴对杆的作用力大小为 D.水平转轴对杆的作用力大小为
【解析】 小球运动到最高点时,杆对小球恰好无作用力(【点拨】小球 所受
重力提供全部向心力。),即重力恰好提供向心力,有,解得 。
由于、两球的角速度相等,则小球的速度 。
小球到最高点时,对杆无弹力,小球 所受重力和拉力的合力提供向心力,
有,解得 。
. .
18.(2024广东中山纪念中学检测)如图所示,质量为、半径为
的光滑管状细圆环用轻杆固定在竖直平面内,、 两小球的直径均略小
于管的内径,它们的质量分别为、。某时刻,、
两球分别位于圆环最低点和最高点,且的速度大小为 ,此
时杆的下端受到向上的压力,大小为。则球的速度大小为
取 ( )
C
A. B. C. D.
【解析】 对球,合力提供向心力,设环对球的支持力为 ,由牛顿第二定律有
,代入数据解得,由牛顿第三定律可得, 球对环的力向下,
大小为。设球对环的力为,由环受力平衡可得 ,解
得,负号表示与重力方向相反,由牛顿第三定律可得,环对球的力 为
、方向竖直向下,对球由牛顿第二定律有,解得 ,
故选C。
题组3 拱桥模型
19.(2024黑龙江哈尔滨开学考试)哈尔滨
某游乐园中的过山车及轨道简化为如图所示
的模型,过山车(可视为质点)先以
的速度经过半径为的圆弧轨道最低点 ,
B
A.过山车经过点时的速度大小为
B.过山车经过点时对该乘客的作用力大小为
C.过山车经过 点时该乘客受到的合力大小为0
D.过山车经过点时对该乘客的作用力大小为
后无动力地冲上半径为的圆弧轨道最高点。已知、两点间的高度差为 ,
过山车中某乘客的质量为,不计阻力,取 ,则( )
【解析】 过山车从到 的过程,不计阻力,根据机械能守恒定律可得
,解得 。
过山车经过点时,由牛顿第二定律有 ,解得乘客受到的支持力大
小为 。
过山车经过点时,由牛顿第二定律有 ,解得该乘客受到
的合力大小和乘客受到的作用力大小分别为, 。
考点5 离心运动与近心运动
20.(2023河南焦作模拟)在东北严寒的冬天,人们经常玩一项“泼水成冰”的游戏,具
体操作是把一杯开水沿弧线均匀快速地泼向空中。图甲是某人玩“泼水成冰”游戏的瞬间,
其示意图如图乙所示。若泼水过程中杯子的运动可看成匀速圆周运动,人的手臂伸直,
在内带动杯子旋转了 ,人的臂长约为 。下列说法正确的是( )
D
A.泼水时杯子的旋转方向为顺时针方向
B. 位置飞出的小水珠初速度沿1方向
C.杯子在旋转时的角速度大小为
D.杯子在旋转时的线速度大小约为
【解析】 由题图乙中飞出的小水珠的运动轨迹可知,泼水时杯子的旋转方向
为逆时针方向, 位置飞出的小水珠初速度沿2方向。
杯子旋转的角速度(【点拨】 。
注意单位的换算。)。
杯子做匀速圆周运动(旋转)的轨迹半径约为 ,则线速度大小约为
。
. .
21.(2024天津南开期中)如图为旋转脱水拖把的结构图,旋转杆上有长度为 的螺
杆,螺杆的螺距(相邻螺纹之间的距离)为 ,固定套杆内部有与旋转杆的螺纹
相配套的凹纹,如果旋转杆不动,固定套杆可以在旋转杆上沿其轴线旋转上行或下行。
把拖把头放置于脱水桶中,手握固定套杆向下运动,固定套杆就会给旋转杆施加驱动力,
驱动旋转杆使拖把头和脱水桶一起转动,把拖把上的水甩出去。拖把头的托盘半径为
,拖布条的长度为,脱水桶的半径为。某次脱水时,固定套杆在 内
匀速下压了 ,该过程中拖把头匀速转动,则下列说法正确的是( )
A.拖把头转动的周期为
B.拖把头转动的角速度为
C.紧贴脱水桶内壁的拖布条上附着的水最不容易被
甩出
D.旋转时脱水桶内壁的点与托盘边缘处的点的向心
加速度大小之比为
√
【解析】 旋转杆上有长度为的螺杆,螺杆的螺距为 ,所以共7圈螺
纹,由题知固定套杆在内匀速下压了,即 转了7周,则拖把头转动的周期为
。
根据周期和角速度的关系式可知 。
所有的拖布条上附着的水转动的角速度都相同,而紧贴脱水桶内壁的拖布条上附
着的水运动半径最大,根据 可知,运动半径越大,需要的向心力越大,越容
易被甩出。
脱水桶的半径为,托盘的半径为,根据 可知,脱水桶内壁的
点与托盘边缘处的点的向心加速度大小之比为 。
觉醒集训
1.(2025辽宁名校联盟联考)如图所示,半径为 的鼓形轮可
绕固定的光滑水平轴 转动。在轮上沿相互垂直的直径方向固
定四根直杆,杆上分别固定有质量均为的、、、 四个
小球,球心与的距离均为 。现让鼓形轮匀速转动,若某时
刻、两球所在直杆恰好位于水平方向,小球 的速度大小为
,不计空气阻力,重力加速度为 ,下列说法正确的是( )
D
A.鼓形轮的角速度为 B.杆对小球 的作用力一定竖直向上
C.杆对小球的作用力为 D.杆对小球的作用力一定大于
【解析】 鼓形轮的角速度为 。
小球所需的向心力大小为 (【点拨】四个小球的角速度和做圆周运动的
半径均相等,因此线速度大小也相等。),若,则杆对小球 的作用力竖
直向下。
对于小球,竖直方向有,水平方向有,则杆对小球 的作用力
大小为 。
对于小球,根据牛顿第二定律可得,可知杆对小球 的作用
力一定大于 。
. .
2.[多选](2025安徽名校联盟开学考)如图所示,在点以水平速度 向左
抛出一个质量为 的小球,小球抛出后始终受到水平向右的恒定风力作用,风
力大小。经过一段时间小球到达点,点位于点正下方,重力加速度 取
。下列说法正确的是( )
AC
A.从到运动过程中小球速度最小值为
B.从到运动过程中小球速度最小值为
C.、两点间的距离
D.小球水平方向的速度为零时距点的水平距离
【解析】 小球水平方向的加速度大小为,小球从到 的运
动时间为,从到 的运动过程中小球速度大小为
,当 时,小球速度
最小(【点拨】当小球的合力与小球的速度垂直时,小球的速度最小。),最小值为
。
、两点间的距离 。
小球水平方向的速度为零时距点的水平距离 。
3.[多选](2025广东惠州阶段检查)在第19届杭州
亚运会女子排球决赛中,中国女排以 战胜日本女
排,以六战全胜且一局未失的战绩成功卫冕。如图所
示,排球场的宽为,长为,球网高为 ,发球员
BCD
A.排球做平抛运动的时间为 B.点距地面的高度为
C.排球被击出时的速度大小为 D.排球着地时的速度大小为
在底线中点正上方的点将排球水平击出,排球恰好擦着网落在对方场地边线上的
点,,不计空气阻力,重力加速度大小为 ,下列说法正确的是 ( )
【解析】 排球做平抛运动的轨迹在地面上的
投影为线段(【点拨】 即排球的水平位移大
小。),如图所示,由几何关系可得 ,所
以排球在左、右场地运动的时间之比为 。设排球做
平抛运动的时间为,点距地面的高度为 ,则有
, ,解得
, 。
. .
. .
根据几何关系可得 ,则排球被击出时的速度大小为
。
排球着地时的速度大小为 。
4.(2025河北衡水中学测评)图甲所示装置为灭火火箭筒,主要用于实施远距离高效、
安全灭火作业。在一次消防演练中,消防员在同一位置用火箭筒先后两次以相同速率、
不同角度发射火箭弹,火箭弹均击中着火点,火箭弹的两次运动轨迹如图乙所示。忽略
空气阻力,下列说法正确的是( )
A.不同轨迹的火箭弹,击中着火点时的速度相同
B.不同轨迹的火箭弹,运动过程中速度变化量相同
C.火箭弹沿轨迹1的运动时间大于沿轨迹2的运动时间
D.火箭弹沿轨迹1的最小速度大于沿轨迹2的最小速度
√
【解析】 第一步:由水平方向的分运动分析运动时间和最小速度。
设初速度方向与水平方向夹角为 ,水平方向分位移均为,则有 ,
解得 ,沿轨迹1的初速度方向与水平方向夹角大一些,则火箭弹沿轨迹1的运
动时间大于沿轨迹2的运动时间。
火箭弹水平方向做匀速直线运动,运动到最高点速度最小,该最小速度等于水平
方向的速度,则有 ,由于沿轨迹1的初速度方向与水平方向夹角大一些,
则火箭弹沿轨迹1的最小速度小于沿轨迹2的最小速度。
第二步:通过竖直方向的分运动分析速度的变化量。
斜抛运动加速度为重力加速度,根据,解得 ,由于沿轨迹1
的初速度方向与水平方向夹角大一些,则火箭弹沿轨迹1运动过程中的速度变化量大于
沿轨迹2运动过程中的速度变化量。
第三步:结合运动的合成与分解求落地瞬间的速度。
火箭弹发射点与击中点的竖直高度相等,设为 ,则有
,则在击中点的速度大小 ,解
得,可知击中着火点时的速度大小相等,令该速度与水平方向夹角为 ,
则有 ,由于击中着火点时的速度方向不同,则不同轨迹的火箭
弹击中着火点时的速度不相同。
跳跳学长 敲黑板
斜抛运动分析要点
(1)运动分解:将斜抛运动分解为水平方向上的匀速直线运动和竖直方向上的匀变速
直线运动,如果为斜上抛,则竖直方向上的分运动可视为竖直上抛运动。
(2)用好对称:相对于运动的最高点,要注意在竖直方向上运动的对称性,如时间对
称、竖直分速度对称和竖直位移对称等。
(3)一个注意:斜上抛运动的物体到达最高点时速度不为零,此时速度大小等于抛出
时的水平分速度大小。
5.(2024四川成都石室中学期中)在光滑的水平面上,一质量 的滑块,在水平
恒定外力 的作用下运动,如图所示给出了滑块在水平面上运动的一段轨迹,滑
块经过、两点时速度大小均为。滑块在点的速度方向与、 连线夹角
, ,则下列说法正确的是( )
C
A.水平恒力的方向与、连线成 夹角
B.滑块从点到 点做匀速圆周运动
C.滑块从点到点的过程中动能最小值为
D.、两点间距离为
【解析】 因为滑块经过、两点的速度大小相等,所以外力的方向垂直于、
的连线(【点拨】可用能量的观点进行分析。滑块的动能不变,水平恒力做功为零,滑
块在力的方向上位移为零。)。
由于滑块在运动过程中受到恒力的作用,故运动轨迹应该为抛物线,滑块不做匀
速圆周运动。
垂直水平恒力方向的分速度为零时,滑块速度最小,由速度分解可知
,最小动能为 。
、之间的距离为 。
. .
. .
6.(2025湖北部分重点中学开学考)如图所示,半径为
的半球形陶罐固定在可以绕竖直轴转动的水平转台上,
转台转轴与过陶罐球心的对称轴 重合。转台以一定
角速度匀速转动,一质量为 的小物块(可视为质点)
落入陶罐内,经过一段时间后小物块随陶罐一起转动且
相对罐壁静止。小物块与陶罐内壁间的动摩擦因数为 ,
B
A.当时,小物块与陶罐内壁间的弹力为
B.当时,小物块与陶罐内壁间的弹力为
C.当 时,小物块与陶罐内壁间的摩擦力沿罐壁向上
D.当 时,小物块将向陶罐上沿滑动
且它和点的连线与之间的夹角为 ,最大静摩擦力等于滑动摩擦力,转动角速度为
,重力加速度为 。则下列说法正确的是( )
【解析】 小物块随转台的转动做水平面内的匀速圆周运动,转台转动的角速度不同,
小物块受到的支持力和摩擦力也不同,因此存在小物块不受摩擦力的临界状态及小物块
正要向陶罐上沿滑动的临界状态。
对物块受力分析可知,物块受重力、支持力和静摩擦力,三个力的合力使物
块做水平面上的圆周运动,转动的角速度不同,物块所受的支持力和静摩擦力均不同,
若静摩擦力为零,根据正交分解和牛顿第二定律可得 ,
,解得。故当 时,小物块与陶罐内壁间的弹力大小
为 。
当 时,小物块与陶罐内壁间的摩擦力为零。
小物块向陶罐上沿滑动的临界条件为物块受
沿切线方向向下的最大静摩擦力 ,受力分析如
图所示,则 ,
,解得
,因此当
时,小物块并未向陶罐上沿滑
动。
7.(2024江西卷)雪地转椅是一种游乐项目,其中心传动装置带动转椅在雪地上滑动。如
图甲、乙所示,传动装置有一高度可调的水平圆盘,可绕通过中心 点的竖直轴匀速转
动。圆盘边缘处固定连接一轻绳,轻绳另一端 连接转椅(视为质点)。转椅运动稳定
后,其角速度与圆盘角速度相等。转椅与雪地之间的动摩擦因数为 ,重力加速度为 ,不
计空气阻力。
(1) 在图甲中,若圆盘在水平雪地上以角速度 匀速转动,转椅运动稳定后在水平雪地
上绕点做半径为的匀速圆周运动。求与之间夹角 的正切值。
【答案】
【解析】 对转椅受力分析,转椅在水平面内受摩擦力 、轻
绳拉力 ,两者合力提供其做圆周运动所需向心力,如图所示,
设转椅的质量为 ,则
转椅所需的向心力
转椅受到的摩擦力
根据几何关系有
联立解得 。
(2) 将圆盘升高,如图乙所示。圆盘匀速转动,转椅运动稳定后在水平雪地上绕 点做
半径为的匀速圆周运动,绳子与竖直方向的夹角为 ,绳子在水平雪地上的投影 与
的夹角为 。求此时圆盘的角速度 。
【答案】
【解析】 转椅在题图乙情况下所需的向心力
转椅受到的摩擦力
根据几何关系有
竖直方向上由平衡条件有
水平面上有
联立解得 。
8.(2025山东烟台阶段练习)如图所示为自由式滑雪大跳台场地的简易图,其中斜坡
、的倾角分别为 、 ,滑雪时运动员由 点静止滑下,进入水平缓
冲区,然后由点离开缓冲区并无碰撞地由点进入段。已知 ,
,重力加速度取,忽略一切阻力和摩擦,运动员经过 点时能量损
失可忽略不计, 。求:
(1) 、 两点间的水平距离;
【答案】
【解析】 运动员在段下滑时,由牛顿第二定律得
解得
运动员从到的过程,有
运动员进入段后做匀速直线运动,然后从点以大小为 的速度开始做平抛运动,
无碰撞地由点进入 段,
由平抛运动的规律可知
解得
则运动员由到的时间为
、两点间的水平距离 。
(2) 运动员由点下滑到 点的总时间。
【答案】
【解析】 运动员由到的过程中,有
由到的过程,有
运动员在段运动时,由牛顿第二定律得
解得
运动员在点的速度为
解得
运动员在段运动的过程,由
解得
运动员由点下滑到点的总时间为
解得 。
【解析】 (1)运动员从到做平抛运动,通过分解平抛运动求、 两点间的水平距
离;(2)先求运动员在各段的运动时间,再求和。
觉醒原创
1.如图所示,一个竖直放置、半径为 的光滑半圆轨道与光滑平
台相连,点和 点分别为半圆轨道的圆心和最低点。在平台上
一轻质弹簧左端与竖直挡板相连,一质量为 的小球将弹簧压
缩,且压缩后的弹性势能。释放小球,小球从 点
进入半圆轨道,且小球进入半圆轨道前已与弹簧分离,小球在
点与半圆轨道分离,现在垂直于 放置一个挡板,
C
A., B.,
C., D.,
挡板最下端在连线上,欲使小球垂直击中挡板,不计空气阻力。关于、 间的距离和挡
板的长度 的要求,下列关系式正确的是( )
【解析】 设小球在点与半圆轨道分离时速度与水平方向的夹角为 ,由功能关
系可知,在
点,由牛顿第二定律得,联立解得, 。最终小球要
垂直击中挡板,则其沿方向分速度减为0,将重力加速度沿方向和 方向分解。
由运动学公式可知方向有 , ,方向有 ,
解得, 。
2.某高楼发生火灾时,消防员在救火过程中调整水枪出水角
度,使水流恰能水平射入着火位置,如图所示。已知着火位
置距地面高度 ,水枪竖直且喷口距地面高度
,, ,不计空
气阻力,重力加速度 ,水流连续,则( )
A
A.水枪喷口处水流的速度大小为
B.喷口处水流的速度方向与水平方向的夹角为
C.水枪喷口处与着火位置间水柱的总体积可求
D.水柱在空中各处的粗细程度相同
【解析】 第一步:模型建构 对喷出的水在空中的运动过程
进行分析
水在空中做斜上抛运动,末速度水平,作出水在空中的运动
轨迹,如图所示。可将水在空中的运动看成反向的平抛运动,
竖直方向上有,水平方向上有 ,解得
,竖直方向上的初速度大小 ,则水枪喷口处水流的速
度大小
,方向与水平方向夹角的正切值
,可得 ,A正确,B错误。
第二步:分析并得出结论 结合所求信息分析水柱形状与体积
水柱在空中的时间、喷口处水流的速度均已知,要求空中水的总体积,还需要知道喷口
的横截面积,C错误。水柱在空中做减速运动,水流连续,相同时间通过不同截面的水
流量相同,则越向上,水流的横截面越大(【点拨】可类比现实中水从水龙头流出后的
情境,越向下水流越细),D错误。
专题四 曲线运动
考向二 圆周运动
2025年高考物理专题复习资料
考点切片
考点1 描述圆周运动的物理量
1.[多选](2025广西名校联合调研)有一种很火的益智玩具——“磁悬浮
陀螺”,依靠磁场力可以让旋转的陀螺悬浮在空中,如图所示。对处于悬
浮状态的陀螺,下列说法正确的是( )
AD
A.距离陀螺中心越远的点,线速度越大
B.陀螺上各点均处于平衡状态
C.陀螺处于完全失重状态
D.若陀螺绕其中心的转速为,则陀螺上距离中心处质点的向心加速度大小为
【解析】 “磁悬浮陀螺”各点的角速度相同,距离中心越远的点,转动半径越大,
线速度越大。
陀螺上各点做圆周运动,是曲线运动,所以各点不处于平衡状态。
陀螺悬浮在空中,陀螺在竖直方向上受力平衡,既不超重也不失重。
质点的角速度为,向心加速度大小为 。
2.(2025江苏南通阶段练习)、 两艘快艇在湖面上做匀速圆周运动(如图所示),在
相同时间内,它们通过的路程之比是,运动方向改变的角度之比是 ,则它们
( )
A
A.线速度大小之比为 B.角速度大小之比为
C.圆周运动的半径之比为 D.向心加速度大小之比为
【解析】 因为相同时间内快艇通过的路程之比是,根据可得、 的线速
度大小之比为 。
相同时间内快艇运动方向改变的角度之比为,根据 可得角速度大小之比
为 。
根据可得快艇做圆周运动的半径之比为 。
根据 可得快艇向心加速度大小之比为 。
考点2 圆周运动中的传动问题
3.(2025山东齐鲁名校联盟开学考)图甲为胶片电影放映机,放完电影后需要倒胶片。
图乙为倒胶片示意图,将胶片由轮倒到轮上,、 为图示时刻两轮边缘胶片上的两
点,主动轮 轮转动的角速度不变,下列说法正确的是( )
A
A.相同时间内倒到 轮上的胶片长度越来越长
B.从动轮 轮转动的角速度也不变
C.图示时刻、两点的角速度
D.图示时刻、两点的向心加速度
【解析】 胶片由轮倒到轮上,则轮半径逐渐增大,主动轮 轮转动的角速度不
变,根据可知轮边缘的线速度增大,故相同时间内倒到 轮上的胶片长度越来越
长。
由题意可知、轮边缘的线速度始终相等,轮的半径减小,根据 可知从动
轮 轮转动的角速度增大。
题图图示时刻、两点的线速度相等,,根据可知 ,
根据向心加速度公式可知 。
4.(2025云南昆明三校联考)如图甲所示为某用于在纸上遮盖错字的修正带的照片,图
乙为其结构示意图。修正带由出带轮、传动轮、收带轮、基带、出带口等组成。测量可
知出带轮有45齿,半径为,传动轮齿数未知,半径为 ,收带轮有15齿,
半径未知,下列选项正确的是( )
A.使用时,出带轮与收带轮转动方向相反
B.根据题中信息,可以算出传动轮的齿数
C.根据题中信息,不能算出收带轮轴心到齿轮边缘的半径
D.在纸面长时间匀速拉动修正带时,出带轮轴心上缠绕的带盘边缘某点的向心加速度大
小不变
√
【解析】 由于齿轮传动,根据题图乙可知,使用时,出带轮与传动轮转动方向相
反,传动轮与收带轮转动方向相反,则出带轮与收带轮转动方向相同。
由于是齿轮传动,相邻齿之间的间距相等,则有,解得 。
由于是齿轮传动,相邻齿之间的间距相等,则有,解得 ,
可知根据题中信息,能算出收带轮轴心到齿轮边缘的半径。
根据向心加速度的表达式有 ,在纸面长时间匀速拉动修正带时,出带轮轴心
上缠绕的带盘边缘某点所在的圆周半径减小,则向心加速度变大。
5.(2024四川成都外国语学校检测)如图为《天工开物》中记录的“牛转
翻车”,该设备利用畜力转动不同半径齿轮来改变水车的转速,从而将
水运送到高处。图中、 分别为两个齿轮边缘上的点,齿轮半径之比为
;、在同一齿轮上且、到转轴的距离之比为 ,
则在齿轮转动过程中( )
C
A.、的角速度相等 B.的线速度比 的线速度小
C.、的周期之比为 D.、的向心加速度大小之比为
【解析】 第一步:确定半径比。
第二步:确定不变量。
、齿轮传动,,、同轴转动, .
第三步:得出结论。
由和得, 。
由,得,又因, ,
,得, 。
考点3 水平面内圆周运动的3大模型
题组1 圆盘模型
大招27 对应练习
解题觉醒
1.题型特征:物体在转动的粗糙圆盘上随着圆盘做圆周运动,求摩擦力、何时滑动等问题。
2.解题技巧
图甲
(1)单物体圆盘:如图甲所示,直接列 ,求解物体不滑动时圆盘
最大的角速度。
图乙
①求绳子产生拉力时的角速度。列 。
②求两物体一起滑动时的角速度。先用质心法算出,再列 ,求解两物体不滑
动时圆盘最大的角速度。
(2)两物体圆盘:如图乙所示。
6.(2025江苏南通名校联盟调研)摩擦传动是传动装置中的一个重要模型,如图所示的
两个水平放置的轮盘靠摩擦力传动,其中、 分别为两轮盘的轴心,已知两个轮盘甲、
乙的半径比 ,且在正常工作时两轮盘不打滑。今在两轮盘上分别放置两个
由同种材料制成的滑块、,两滑块与轮盘间的动摩擦因数相同,两滑块距离轴心 、
的间距满足 。若轮盘乙由静止开始缓慢地转动起来,且转速逐渐增加,则下
列叙述正确的是( )
①滑块和 在与轮盘相对静止时,角速度之比
为
②滑块和 在与轮盘相对静止时,向心加速度
之比为
③轮盘乙转速增加后滑块 先发生滑动
④轮盘乙转速增加后滑块 先发生滑动
A.①②③ B.①②④ C.②③④ D.①③④
√
【解析】 摩擦传动的物体边缘线速度相等,则轮盘甲、乙边缘的线速度相等。、 与
轮盘相对静止时,分别和轮盘甲、乙做同轴转动,则、 做匀速圆周运动时,角速度
分别等于轮盘甲、乙的角速度。①根据 ,解得
,①正确;②根据可得滑块和 在与轮盘相
对静止时,向心加速度之比为,②正确;、 滑
块受到的摩擦力提供它们做圆周运动的向心力,则滑块恰好与轮盘发生相对滑动时有
,,解得 (【大招运用】根据大
招内容中滑块相对轮盘发生相对滑动的临界角速度,可得 。),
结合可知,转速增加后滑块 先发生滑动,③正确、④错误,故选A。
. .
. .
7.(2024重庆市实验中学模拟)如图甲所示,
两个完全相同的小木块和 (均可视为质
点)用轻绳连接置于水平圆盘上, 与转轴
的距离为 。圆盘从静止开始绕转轴极缓
慢地加速转动,木块和圆盘保持相对静止。
表示圆盘转动的角速度,、 与圆盘保
D
A.图线(1)对应 B.绳长为
C. D.时绳的拉力大小为
持相对静止的过程中所受摩擦力与满足如图乙所示关系,图中 。下列判断正
确的是( )
【解析】 第一步:当 时
对、分别分析:,,,、间绳没有拉力时, ,
图线1对应,图线2对应,由可知,解得 ,绳长
。
第二步:当 时绳子拉紧
对分析: ①
第三步:当时,、 整体开始滑动
对整体分析: ②
对分析:
联立①②解出 。
由题图乙可知,当时,绳上无拉力,木块和 都由各自所受的静摩擦
力提供向心力,,,因为,所以,故图线1对应 。
当时,木块所受的摩擦力恰好达到最大静摩擦力,且, ,
,即,可得,所以绳长为 。
当时,对木块,有,可得;当 时,
对木块,有,对木块,有 ,联立可得
(【大招运用】运用大招27可知 ,
。),所以, 。
. .
. .
. .
8.(2024江苏卷)陶瓷是以粘土为主要原料以及各种天然矿物经过
粉碎混炼、成型和煅烧制得的材料以及各种制品。如图所示是生
产陶瓷的简化工作台,当陶瓷匀速转动时,台面上掉有陶屑,陶
屑与台面间的动摩擦因数处处相等(台面足够大),最大静摩擦
力等于滑动摩擦力,则( )
D
A.离轴越远的陶屑质量越大 B.离轴 越近的陶屑质量越小
C.只有平台边缘有陶屑 D.离轴最远的陶屑距离不会超过某一值
【解析】 与台面相对静止的陶屑做匀速圆周运动,静摩擦力提供向心力,
当静摩擦力为最大静摩擦力时,根据牛顿第二定律可得,解得 ,因
与台面相对静止的这些陶屑的角速度相同,由此可知能与台面相对静止的陶屑离轴
的距离与陶屑质量无关,只要陶屑离轴的距离小于等于 ,陶屑在台面上均不发生
相对滑动,即只要在台面上不发生相对滑动的位置都有陶屑。
离轴 最远的陶屑受到的静摩擦力为最大静摩擦力时,由前述分析可知最大的运
动半径为, 与 均一定,故为定值,即离轴 最远的陶屑距离不超过某一
值。
题组2 圆锥摆模型
大招28 对应练习
解题觉醒
1.题型特征:绳子上端固定在天花板上,下端系着小球,小球在水平面上做匀速圆周运
动或小球在半球形碗(或倒锥桶)中做水平面内的圆周运动。
2.解题技巧
类型 示意图 结论
等长摆 _______________________________________ 更高、更快、更强(小球所处位置越高,线速度、角
速度和向心加速度均越大,向心力也越大)
类型 示意图 结论
等高摆 _____________________________________________ 不变
类型 示意图 结论
倒锥摆 ____________________________________________ 不变
9.[多选](2025福建厦门阶段练习)如图所示,质量为 的小球
用长为的细线悬于点,使小球在水平面内以角速度 做匀速圆
周运动。已知小球做圆周运动时圆心到悬点的距离为 。下列
说法正确的是( )
AC
A.细线对小球的拉力大小为
B.保持不变,增大角速度 ,细线与竖直方向的夹角变小
C.保持不变,增大细线长, 不变
D.保持不变,增大细线长 ,细线对小球拉力的大小不变
【解析】 设细线与竖直方向的夹角为 ,根据牛顿第二定律可得
, ,解得细线对小球的拉力大小为
,,由此可知,保持不变,增大角速度 ,细线与竖直方向的夹
角 变大(【大招运用】根据大招内容中的口诀“更高、更快、更强”,可知增大角速度
,细线与竖直方向的夹角 变大。)。
根据牛顿第二定律可得 ,解得,可知保持 不
变,增大细线长, 不变(【大招运用】根据大招内容可知等高摆的角速度 不
变。),根据 可知,细线对小球的拉力增大。
. .
. .
. .
. .
10.[多选](2025福建福州第一中学开学考)如图所示,两个同轴心的玻璃漏斗内表
面光滑,两漏斗与竖直转轴的夹角分别是 、 且 。、、 三个小球在漏斗
上做匀速圆周运动,、两球在同一漏斗的不同位置,球在另一个漏斗上且与 球位
置等高,下列说法正确的是( )
BC
A.球与球受到的支持力一定大小相等 B.球与 球的向心加速度一定大小相等
C.球与球的速度一定大小相等 D.球的周期一定等于 球的周期
【解析】 根据题意可知,球与 球均
做匀速圆周运动,合力提供向心力,分别对
两球受力分析,如图所示,由几何关系,对
球有,对球有,
由几何关系,对球有,对球有 ,根据
,可得球与球的向心加速度满足 (【大招运用】根据大招
内容可知倒锥摆中做匀速圆周运动的小球的加速度不变,可得 。)。
同理可知,球的向心力为,根据可知, 球做圆周运动
球与 球质量关系不确定,受到的支持力大小不一定相等。
. .
的速度为,同理可知,球做圆周运动的速度为,设球与 球距
离倒锥顶点的高度为(【易错】此处易错误地将球和 球看成等高摆。),由几何关
系可得 ,,可得,由公式 可知,由于
,则有 。
. .
. .
11.(2024辽宁大连期末)如图所示,一质量为的小球(可视为质点)由轻绳和 分
别系于一竖直细杆的点和点,、间的距离与两轻绳长度均为 。已知重力加速度
为,当小球随杆绕竖直轴以角速度 匀速转动时,下列说法正确的是( )
D
A.当时, 绳恰好没有拉力
B.当时,绳的拉力大小为
C.当绳有拉力时,总是比绳拉力小
D.当时,绳的拉力大小为
【解析】
时, 绳恰好 没有拉力 A( )
, 绳没有拉力 , ,解得 , B( )
绳有拉力时 , , 解得 C( )
, 绳 有拉力 , , 解得 D(√)
题组3 火车转弯模型
12.[多选](2024河南周口阶段练习)在修筑铁路时,弯道处的外轨会略高于内轨。
如图所示,当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时
的速度大小为,重力加速度为,两轨所在面的倾角为 ,则( )
ABD
A.该弯道的半径
B.当火车质量改变时,规定的行驶速度大小不变
C.当火车速率大于 时,内轨将受到轮缘的挤压
D.当火车速率小于 时,内轨将受到轮缘的挤压
【解析】 当火车以速率 转弯时,恰好由重力和支持力的合力提供向心力,
由牛顿第二定律可得,解得, ,该临界速度与火
车质量无关,故当火车质量改变时,规定的行驶速度大小不变。
当火车速率大于 时,重力与支持力的合力不足以提供向心力,火车有做离心运动
的趋势,故外轨将受到轮缘的挤压。
当火车速率小于 时,重力与支持力的合力大于所需的向心力,火车有做向心运动
的趋势,内轨将受到轮缘的挤压。
13.(2025广东汕头开学考)汽车的自动泊车系统持续发展,现有更先进的“全自动泊
车”。如图所示为某次电动汽车自动泊车全景示意图。汽车按图示路线(半径为的
圆弧与长为的直线构成)顺利停车,用时。汽车与地面间的动摩擦因数为
(最大静摩擦力等于滑动摩擦力),重力加速度取 ,汽车可视为质点,下列
说法正确的是( )
C
A.汽车在转弯过程中做匀变速曲线运动
B.汽车在转弯过程中的最大允许速度约为
C.汽车泊车的平均速度约为
D.汽车在泊车过程中受到的摩擦力总是与运动方向相反
【解析】 汽车在转弯过程中受到的摩擦力方向时刻变化,合外力方向也时刻变化,
所以汽车所做的运动不是匀变速曲线运动。
汽车转弯过程中靠静摩擦力提供向心力,又因为最大静摩擦力等于滑动摩擦力,
有,代入数据解得 。
汽车泊车过程的位移大小为 ,则汽车泊车的平均速
度约为 (【提醒】注意C选项要求的是平均速度,而不是
平均速率。)。
汽车在泊车过程中沿圆弧运动时所受摩擦力为提供向心力的静摩擦力和与运动方
向相反的摩擦力的合力,因此汽车在泊车过程中受到的摩擦力不总是与运动方向相反。
. .
. .
考点4 竖直面内圆周运动的3大模型
大招29 对应练习
解题觉醒
1.题型特征:物体在竖直平面内做圆周运动。
2.解题技巧
绳模型 杆模型 拱桥/凹形路面
最低 点 最高 点 速度较小时: 速度较大时:
绳模型 杆模型 拱桥/凹形路面
速度 最值 最高点最小速 度为 最高点最小速度为0 不脱离路面行驶的最大速度为
题组1 竖直圆绳模型
14.(2025山西大同一中月考)如图所示,竖直平面内的光滑圆轨道
半径为,、 点分别为轨道的最左侧、最高点。一小球在轨道内运
动且始终未离开轨道,重力加速度为 ,则( )
D
A.若小球运动到 点,小球在该位置所受的合力指向圆心
B.若小球运动到 点,小球在该位置的速度一定大于0
C.若小球运动到 点,小球在该位置一定受到轨道弹力
D.若小球运动到点,小球在该位置的速度一定大于等于
【解析】 若小球运动到 点,且小球在该位置受到的轨道弹力指向圆心,但重力
竖直向下,所以小球在该位置所受的合力不指向圆心。
若小球运动到 点,且小球在该位置的速度如果刚好等于0,则小球将在下半圆轨
道内来回运动,始终不会离开轨道。
若小球运动到 点,重力刚好提供向心力,则此时小球受到的轨道弹力刚好为
0,则有,可得,可知若小球运动到 点,在该位置的速度一定大
于等于 (【大招运用】根据大招内容可知绳模型中小球在最高点的最小速度为
。 )。
. .
. .
15.(2024江西南昌二中模拟)如图甲所示,小球用不可伸长的轻绳连接,绕定点 在竖
直面内做圆周运动,小球经过最高点时的速度大小为,此时轻绳拉力大小为 ,拉力
与速度的平方的关系如图乙所示,图像中的数据和以及重力加速度 都为已知量,
以下说法正确的是( )
C
A.数据 与小球的质量有关
B.数据 与小球的质量无关
C.比值 与小球的质量和圆周轨道半径都有关
D.利用数据、和 不能够求出小球的质量和圆周
轨道半径
【解析】 当时,轻绳的拉力为零,小球的重力提供向心力,设轻绳长为 ,
则有,解得,即,故数据 与小球的质量无关。
当时,对小球受力分析,有,解得,故数据 与小球
的质量有关。
根据以上分析可知,比值与小球的质量和圆周轨道半径(即轻绳长 )都有
关。
由以上分析可得, 。
跳跳学长 有话说
小球在拉力作用下通过最高点时,重力与拉力的合力提供向心力,
,运用图像的斜率和纵截距可知, ,
,则, ,A、B、D错误,C正确。
16.(2025山西吕梁阶段练习)如图所示,质量为的小物块用长为的细线悬挂于 点,
给物块一个水平初速度使其在竖直面内做圆周运动,物块运动到最低点时,细线的拉力
大小等于。斜面体固定在水平地面上,斜面长为,倾角为 , 竖直
且长也为。若物块做圆周运动到最低点时细线突然断开,此后物块恰好从 点无碰撞
地滑上斜面,最终落在地面上,物块与斜面间的动摩擦因数为,重力加速度为 ,
空气阻力不计,求:
(1) 小物块做圆周运动在最低点时的速度大小;
【答案】
【解析】 设物块运动到最低点时速度为,根据牛顿第二定律有
解得 。
(2) 小物块在斜面上运动的时间;
【答案】
【解析】 设物块运动到点时速度大小为 ,根据几何关系有
由于 ,因此物块在斜面上做匀速直线运动,在斜面上运动的时间
为 。
(3) 有斜面体时小球的落地点与无斜面体时小球的落地点间的距离。
【答案】
【解析】 物块运动到点时竖直方向的分速度
圆周运动的最低点与点的高度差
点离水平地面的高度
没有斜面体时,物块做平抛运动的水平位移
有斜面体时,物块做平抛运动下降高度,所经过的水平位移
. .
物块落地点离圆周运动最低点间的水平距离 (【点拨】
物块在斜面上做匀速直线运动,因此物块运动到点时的速度和物块到达 点时的速度
相等,物块运动到点后刚好“接着”物块到达 点时的运动继续做抛体运动,可将两个
运动过程合在一起等效为一个完整的平抛运动过程。)
则有斜面体时物块的落地点与无斜面体时物块的落地点间的距离为
。
. .
题组2 竖直圆杆模型
17.(2024陕西西安期中)如图所示,轻杆长为 ,在杆两端分别固
定质量均为的小球和,光滑水平转轴穿过杆上距小球为 处的
点。外界给系统一定能量后,杆和小球在竖直平面内转动,小球
运动到最高点时,杆对小球 恰好无作用力,忽略空气阻力,重力加
速度为。则小球 在最高点时( )
C
A.小球的速度为零 B.小球的速度大小为
C.水平转轴对杆的作用力大小为 D.水平转轴对杆的作用力大小为
【解析】 小球运动到最高点时,杆对小球恰好无作用力(【点拨】小球 所受
重力提供全部向心力。),即重力恰好提供向心力,有,解得 。
由于、两球的角速度相等,则小球的速度 。
小球到最高点时,对杆无弹力,小球 所受重力和拉力的合力提供向心力,
有,解得 。
. .
18.(2024广东中山纪念中学检测)如图所示,质量为、半径为
的光滑管状细圆环用轻杆固定在竖直平面内,、 两小球的直径均略小
于管的内径,它们的质量分别为、。某时刻,、
两球分别位于圆环最低点和最高点,且的速度大小为 ,此
时杆的下端受到向上的压力,大小为。则球的速度大小为
取 ( )
C
A. B. C. D.
【解析】 对球,合力提供向心力,设环对球的支持力为 ,由牛顿第二定律有
,代入数据解得,由牛顿第三定律可得, 球对环的力向下,
大小为。设球对环的力为,由环受力平衡可得 ,解
得,负号表示与重力方向相反,由牛顿第三定律可得,环对球的力 为
、方向竖直向下,对球由牛顿第二定律有,解得 ,
故选C。
题组3 拱桥模型
19.(2024黑龙江哈尔滨开学考试)哈尔滨
某游乐园中的过山车及轨道简化为如图所示
的模型,过山车(可视为质点)先以
的速度经过半径为的圆弧轨道最低点 ,
B
A.过山车经过点时的速度大小为
B.过山车经过点时对该乘客的作用力大小为
C.过山车经过 点时该乘客受到的合力大小为0
D.过山车经过点时对该乘客的作用力大小为
后无动力地冲上半径为的圆弧轨道最高点。已知、两点间的高度差为 ,
过山车中某乘客的质量为,不计阻力,取 ,则( )
【解析】 过山车从到 的过程,不计阻力,根据机械能守恒定律可得
,解得 。
过山车经过点时,由牛顿第二定律有 ,解得乘客受到的支持力大
小为 。
过山车经过点时,由牛顿第二定律有 ,解得该乘客受到
的合力大小和乘客受到的作用力大小分别为, 。
考点5 离心运动与近心运动
20.(2023河南焦作模拟)在东北严寒的冬天,人们经常玩一项“泼水成冰”的游戏,具
体操作是把一杯开水沿弧线均匀快速地泼向空中。图甲是某人玩“泼水成冰”游戏的瞬间,
其示意图如图乙所示。若泼水过程中杯子的运动可看成匀速圆周运动,人的手臂伸直,
在内带动杯子旋转了 ,人的臂长约为 。下列说法正确的是( )
D
A.泼水时杯子的旋转方向为顺时针方向
B. 位置飞出的小水珠初速度沿1方向
C.杯子在旋转时的角速度大小为
D.杯子在旋转时的线速度大小约为
【解析】 由题图乙中飞出的小水珠的运动轨迹可知,泼水时杯子的旋转方向
为逆时针方向, 位置飞出的小水珠初速度沿2方向。
杯子旋转的角速度(【点拨】 。
注意单位的换算。)。
杯子做匀速圆周运动(旋转)的轨迹半径约为 ,则线速度大小约为
。
. .
21.(2024天津南开期中)如图为旋转脱水拖把的结构图,旋转杆上有长度为 的螺
杆,螺杆的螺距(相邻螺纹之间的距离)为 ,固定套杆内部有与旋转杆的螺纹
相配套的凹纹,如果旋转杆不动,固定套杆可以在旋转杆上沿其轴线旋转上行或下行。
把拖把头放置于脱水桶中,手握固定套杆向下运动,固定套杆就会给旋转杆施加驱动力,
驱动旋转杆使拖把头和脱水桶一起转动,把拖把上的水甩出去。拖把头的托盘半径为
,拖布条的长度为,脱水桶的半径为。某次脱水时,固定套杆在 内
匀速下压了 ,该过程中拖把头匀速转动,则下列说法正确的是( )
A.拖把头转动的周期为
B.拖把头转动的角速度为
C.紧贴脱水桶内壁的拖布条上附着的水最不容易被
甩出
D.旋转时脱水桶内壁的点与托盘边缘处的点的向心
加速度大小之比为
√
【解析】 旋转杆上有长度为的螺杆,螺杆的螺距为 ,所以共7圈螺
纹,由题知固定套杆在内匀速下压了,即 转了7周,则拖把头转动的周期为
。
根据周期和角速度的关系式可知 。
所有的拖布条上附着的水转动的角速度都相同,而紧贴脱水桶内壁的拖布条上附
着的水运动半径最大,根据 可知,运动半径越大,需要的向心力越大,越容
易被甩出。
脱水桶的半径为,托盘的半径为,根据 可知,脱水桶内壁的
点与托盘边缘处的点的向心加速度大小之比为 。
觉醒集训
1.(2025辽宁名校联盟联考)如图所示,半径为 的鼓形轮可
绕固定的光滑水平轴 转动。在轮上沿相互垂直的直径方向固
定四根直杆,杆上分别固定有质量均为的、、、 四个
小球,球心与的距离均为 。现让鼓形轮匀速转动,若某时
刻、两球所在直杆恰好位于水平方向,小球 的速度大小为
,不计空气阻力,重力加速度为 ,下列说法正确的是( )
D
A.鼓形轮的角速度为 B.杆对小球 的作用力一定竖直向上
C.杆对小球的作用力为 D.杆对小球的作用力一定大于
【解析】 鼓形轮的角速度为 。
小球所需的向心力大小为 (【点拨】四个小球的角速度和做圆周运动的
半径均相等,因此线速度大小也相等。),若,则杆对小球 的作用力竖
直向下。
对于小球,竖直方向有,水平方向有,则杆对小球 的作用力
大小为 。
对于小球,根据牛顿第二定律可得,可知杆对小球 的作用
力一定大于 。
. .
2.[多选](2025安徽名校联盟开学考)如图所示,在点以水平速度 向左
抛出一个质量为 的小球,小球抛出后始终受到水平向右的恒定风力作用,风
力大小。经过一段时间小球到达点,点位于点正下方,重力加速度 取
。下列说法正确的是( )
AC
A.从到运动过程中小球速度最小值为
B.从到运动过程中小球速度最小值为
C.、两点间的距离
D.小球水平方向的速度为零时距点的水平距离
【解析】 小球水平方向的加速度大小为,小球从到 的运
动时间为,从到 的运动过程中小球速度大小为
,当 时,小球速度
最小(【点拨】当小球的合力与小球的速度垂直时,小球的速度最小。),最小值为
。
、两点间的距离 。
小球水平方向的速度为零时距点的水平距离 。
3.[多选](2025广东惠州阶段检查)在第19届杭州
亚运会女子排球决赛中,中国女排以 战胜日本女
排,以六战全胜且一局未失的战绩成功卫冕。如图所
示,排球场的宽为,长为,球网高为 ,发球员
BCD
A.排球做平抛运动的时间为 B.点距地面的高度为
C.排球被击出时的速度大小为 D.排球着地时的速度大小为
在底线中点正上方的点将排球水平击出,排球恰好擦着网落在对方场地边线上的
点,,不计空气阻力,重力加速度大小为 ,下列说法正确的是 ( )
【解析】 排球做平抛运动的轨迹在地面上的
投影为线段(【点拨】 即排球的水平位移大
小。),如图所示,由几何关系可得 ,所
以排球在左、右场地运动的时间之比为 。设排球做
平抛运动的时间为,点距地面的高度为 ,则有
, ,解得
, 。
. .
. .
根据几何关系可得 ,则排球被击出时的速度大小为
。
排球着地时的速度大小为 。
4.(2025河北衡水中学测评)图甲所示装置为灭火火箭筒,主要用于实施远距离高效、
安全灭火作业。在一次消防演练中,消防员在同一位置用火箭筒先后两次以相同速率、
不同角度发射火箭弹,火箭弹均击中着火点,火箭弹的两次运动轨迹如图乙所示。忽略
空气阻力,下列说法正确的是( )
A.不同轨迹的火箭弹,击中着火点时的速度相同
B.不同轨迹的火箭弹,运动过程中速度变化量相同
C.火箭弹沿轨迹1的运动时间大于沿轨迹2的运动时间
D.火箭弹沿轨迹1的最小速度大于沿轨迹2的最小速度
√
【解析】 第一步:由水平方向的分运动分析运动时间和最小速度。
设初速度方向与水平方向夹角为 ,水平方向分位移均为,则有 ,
解得 ,沿轨迹1的初速度方向与水平方向夹角大一些,则火箭弹沿轨迹1的运
动时间大于沿轨迹2的运动时间。
火箭弹水平方向做匀速直线运动,运动到最高点速度最小,该最小速度等于水平
方向的速度,则有 ,由于沿轨迹1的初速度方向与水平方向夹角大一些,
则火箭弹沿轨迹1的最小速度小于沿轨迹2的最小速度。
第二步:通过竖直方向的分运动分析速度的变化量。
斜抛运动加速度为重力加速度,根据,解得 ,由于沿轨迹1
的初速度方向与水平方向夹角大一些,则火箭弹沿轨迹1运动过程中的速度变化量大于
沿轨迹2运动过程中的速度变化量。
第三步:结合运动的合成与分解求落地瞬间的速度。
火箭弹发射点与击中点的竖直高度相等,设为 ,则有
,则在击中点的速度大小 ,解
得,可知击中着火点时的速度大小相等,令该速度与水平方向夹角为 ,
则有 ,由于击中着火点时的速度方向不同,则不同轨迹的火箭
弹击中着火点时的速度不相同。
跳跳学长 敲黑板
斜抛运动分析要点
(1)运动分解:将斜抛运动分解为水平方向上的匀速直线运动和竖直方向上的匀变速
直线运动,如果为斜上抛,则竖直方向上的分运动可视为竖直上抛运动。
(2)用好对称:相对于运动的最高点,要注意在竖直方向上运动的对称性,如时间对
称、竖直分速度对称和竖直位移对称等。
(3)一个注意:斜上抛运动的物体到达最高点时速度不为零,此时速度大小等于抛出
时的水平分速度大小。
5.(2024四川成都石室中学期中)在光滑的水平面上,一质量 的滑块,在水平
恒定外力 的作用下运动,如图所示给出了滑块在水平面上运动的一段轨迹,滑
块经过、两点时速度大小均为。滑块在点的速度方向与、 连线夹角
, ,则下列说法正确的是( )
C
A.水平恒力的方向与、连线成 夹角
B.滑块从点到 点做匀速圆周运动
C.滑块从点到点的过程中动能最小值为
D.、两点间距离为
【解析】 因为滑块经过、两点的速度大小相等,所以外力的方向垂直于、
的连线(【点拨】可用能量的观点进行分析。滑块的动能不变,水平恒力做功为零,滑
块在力的方向上位移为零。)。
由于滑块在运动过程中受到恒力的作用,故运动轨迹应该为抛物线,滑块不做匀
速圆周运动。
垂直水平恒力方向的分速度为零时,滑块速度最小,由速度分解可知
,最小动能为 。
、之间的距离为 。
. .
. .
6.(2025湖北部分重点中学开学考)如图所示,半径为
的半球形陶罐固定在可以绕竖直轴转动的水平转台上,
转台转轴与过陶罐球心的对称轴 重合。转台以一定
角速度匀速转动,一质量为 的小物块(可视为质点)
落入陶罐内,经过一段时间后小物块随陶罐一起转动且
相对罐壁静止。小物块与陶罐内壁间的动摩擦因数为 ,
B
A.当时,小物块与陶罐内壁间的弹力为
B.当时,小物块与陶罐内壁间的弹力为
C.当 时,小物块与陶罐内壁间的摩擦力沿罐壁向上
D.当 时,小物块将向陶罐上沿滑动
且它和点的连线与之间的夹角为 ,最大静摩擦力等于滑动摩擦力,转动角速度为
,重力加速度为 。则下列说法正确的是( )
【解析】 小物块随转台的转动做水平面内的匀速圆周运动,转台转动的角速度不同,
小物块受到的支持力和摩擦力也不同,因此存在小物块不受摩擦力的临界状态及小物块
正要向陶罐上沿滑动的临界状态。
对物块受力分析可知,物块受重力、支持力和静摩擦力,三个力的合力使物
块做水平面上的圆周运动,转动的角速度不同,物块所受的支持力和静摩擦力均不同,
若静摩擦力为零,根据正交分解和牛顿第二定律可得 ,
,解得。故当 时,小物块与陶罐内壁间的弹力大小
为 。
当 时,小物块与陶罐内壁间的摩擦力为零。
小物块向陶罐上沿滑动的临界条件为物块受
沿切线方向向下的最大静摩擦力 ,受力分析如
图所示,则 ,
,解得
,因此当
时,小物块并未向陶罐上沿滑
动。
7.(2024江西卷)雪地转椅是一种游乐项目,其中心传动装置带动转椅在雪地上滑动。如
图甲、乙所示,传动装置有一高度可调的水平圆盘,可绕通过中心 点的竖直轴匀速转
动。圆盘边缘处固定连接一轻绳,轻绳另一端 连接转椅(视为质点)。转椅运动稳定
后,其角速度与圆盘角速度相等。转椅与雪地之间的动摩擦因数为 ,重力加速度为 ,不
计空气阻力。
(1) 在图甲中,若圆盘在水平雪地上以角速度 匀速转动,转椅运动稳定后在水平雪地
上绕点做半径为的匀速圆周运动。求与之间夹角 的正切值。
【答案】
【解析】 对转椅受力分析,转椅在水平面内受摩擦力 、轻
绳拉力 ,两者合力提供其做圆周运动所需向心力,如图所示,
设转椅的质量为 ,则
转椅所需的向心力
转椅受到的摩擦力
根据几何关系有
联立解得 。
(2) 将圆盘升高,如图乙所示。圆盘匀速转动,转椅运动稳定后在水平雪地上绕 点做
半径为的匀速圆周运动,绳子与竖直方向的夹角为 ,绳子在水平雪地上的投影 与
的夹角为 。求此时圆盘的角速度 。
【答案】
【解析】 转椅在题图乙情况下所需的向心力
转椅受到的摩擦力
根据几何关系有
竖直方向上由平衡条件有
水平面上有
联立解得 。
8.(2025山东烟台阶段练习)如图所示为自由式滑雪大跳台场地的简易图,其中斜坡
、的倾角分别为 、 ,滑雪时运动员由 点静止滑下,进入水平缓
冲区,然后由点离开缓冲区并无碰撞地由点进入段。已知 ,
,重力加速度取,忽略一切阻力和摩擦,运动员经过 点时能量损
失可忽略不计, 。求:
(1) 、 两点间的水平距离;
【答案】
【解析】 运动员在段下滑时,由牛顿第二定律得
解得
运动员从到的过程,有
运动员进入段后做匀速直线运动,然后从点以大小为 的速度开始做平抛运动,
无碰撞地由点进入 段,
由平抛运动的规律可知
解得
则运动员由到的时间为
、两点间的水平距离 。
(2) 运动员由点下滑到 点的总时间。
【答案】
【解析】 运动员由到的过程中,有
由到的过程,有
运动员在段运动时,由牛顿第二定律得
解得
运动员在点的速度为
解得
运动员在段运动的过程,由
解得
运动员由点下滑到点的总时间为
解得 。
【解析】 (1)运动员从到做平抛运动,通过分解平抛运动求、 两点间的水平距
离;(2)先求运动员在各段的运动时间,再求和。
觉醒原创
1.如图所示,一个竖直放置、半径为 的光滑半圆轨道与光滑平
台相连,点和 点分别为半圆轨道的圆心和最低点。在平台上
一轻质弹簧左端与竖直挡板相连,一质量为 的小球将弹簧压
缩,且压缩后的弹性势能。释放小球,小球从 点
进入半圆轨道,且小球进入半圆轨道前已与弹簧分离,小球在
点与半圆轨道分离,现在垂直于 放置一个挡板,
C
A., B.,
C., D.,
挡板最下端在连线上,欲使小球垂直击中挡板,不计空气阻力。关于、 间的距离和挡
板的长度 的要求,下列关系式正确的是( )
【解析】 设小球在点与半圆轨道分离时速度与水平方向的夹角为 ,由功能关
系可知,在
点,由牛顿第二定律得,联立解得, 。最终小球要
垂直击中挡板,则其沿方向分速度减为0,将重力加速度沿方向和 方向分解。
由运动学公式可知方向有 , ,方向有 ,
解得, 。
2.某高楼发生火灾时,消防员在救火过程中调整水枪出水角
度,使水流恰能水平射入着火位置,如图所示。已知着火位
置距地面高度 ,水枪竖直且喷口距地面高度
,, ,不计空
气阻力,重力加速度 ,水流连续,则( )
A
A.水枪喷口处水流的速度大小为
B.喷口处水流的速度方向与水平方向的夹角为
C.水枪喷口处与着火位置间水柱的总体积可求
D.水柱在空中各处的粗细程度相同
【解析】 第一步:模型建构 对喷出的水在空中的运动过程
进行分析
水在空中做斜上抛运动,末速度水平,作出水在空中的运动
轨迹,如图所示。可将水在空中的运动看成反向的平抛运动,
竖直方向上有,水平方向上有 ,解得
,竖直方向上的初速度大小 ,则水枪喷口处水流的速
度大小
,方向与水平方向夹角的正切值
,可得 ,A正确,B错误。
第二步:分析并得出结论 结合所求信息分析水柱形状与体积
水柱在空中的时间、喷口处水流的速度均已知,要求空中水的总体积,还需要知道喷口
的横截面积,C错误。水柱在空中做减速运动,水流连续,相同时间通过不同截面的水
流量相同,则越向上,水流的横截面越大(【点拨】可类比现实中水从水龙头流出后的
情境,越向下水流越细),D错误。
同课章节目录
