考向二 宇宙航行问题-2025年高考物理专题复习课件
文档属性
| 名称 | 考向二 宇宙航行问题-2025年高考物理专题复习课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-02-18 09:45:54 | ||
图片预览










文档简介
(共45张PPT)
专题五 万有引力与航天
考向二 宇宙航行问题
2025年高考物理专题复习资料
考点切片
考点1 宇宙速度
1.(2025山西吕梁开学考试)2024年5月8日,嫦娥六号探测器在北京航天飞行控制中心
的精确控制下,成功实施近月制动,顺利进入环月轨道飞行。嫦娥六号探测器的环月轨
道飞行可看成匀速圆周运动,运动周期为。已知月球质量与地球质量的比值为 ,月
球半径与地球半径的比值为,地球半径为,地球表面的重力加速度大小为 ,引力常
量为 ,则( )
B
A.嫦娥六号探测器发射的速度应大于第二宇宙速度小于第三宇宙速度
B.嫦娥六号探测器的环月轨道距月球表面的高度为
C.月球的第一宇宙速度大小为
D.月球表面的重力加速度大小为
【解析】 嫦娥六号探测器没有脱离地球引力,所以嫦娥六号探测器发射的速度应
大于第一宇宙速度小于第二宇宙速度。
在地球表面上有 ,嫦娥六号探测器环月做匀速圆周运动有
,联立解得 。
设月球的第一宇宙速度(【点拨】月球的第一宇宙速度等于近月卫星的线速度,是
环月卫星最大的环绕速度,也是在月球表面发射卫星的最小发射速度。)大小为 ,则有
,解得 。
在月球表面上有,解得 。
2.(2023湖南卷)根据宇宙大爆炸理论,密度较大区域的物质在万有引力作用下,不断
聚集可能形成恒星。恒星最终的归宿与其质量有关,如果质量为太阳质量的 倍将
坍缩成白矮星,质量为太阳质量的 倍将坍缩成中子星,质量更大的恒星将坍缩
成黑洞。设恒星坍缩前后可看成质量均匀分布的球体,质量不变,体积缩小,自转变快。
不考虑恒星与其他物体的相互作用。已知逃逸速度为第一宇宙速度的 倍,中子星密
度大于白矮星。根据万有引力理论,下列说法正确的是( )
B
A.同一恒星表面任意位置的重力加速度相同
B.恒星坍缩后表面两极处的重力加速度比坍缩前的大
C.恒星坍缩前后的第一宇宙速度不变
D.中子星的逃逸速度小于白矮星的逃逸速度
【解析】恒星自转万有引力有两个效果
从赤道到两极, , , 。
两极 , 。
第一宇宙速度 , 。
逃逸速度 。
跳跳学长 有话说
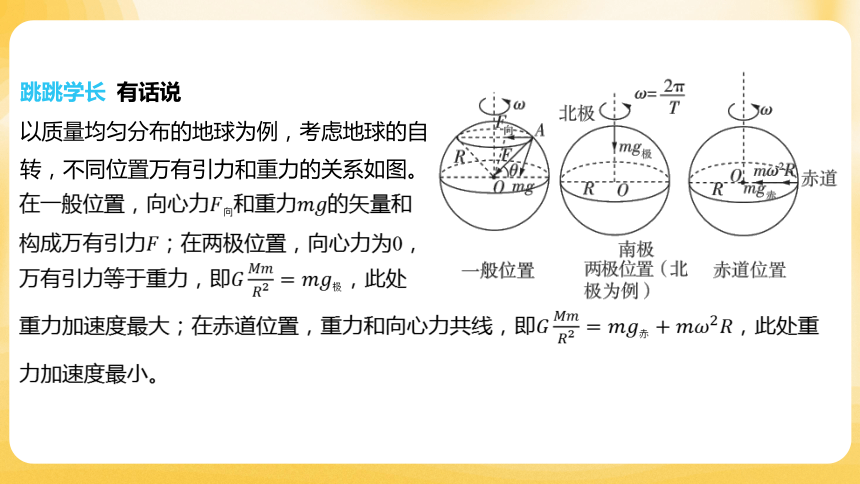
以质量均匀分布的地球为例,考虑地球的自
转,不同位置万有引力和重力的关系如图。
在一般位置,向心力和重力 的矢量和
构成万有引力 ;在两极位置,向心力为0,
万有引力等于重力,即 ,此处
重力加速度最大;在赤道位置,重力和向心力共线,即 ,此处重
力加速度最小。
考点2 近地卫星与同步卫星
3.科技强国(2024广东东莞阶段练习)2022年11月,梦天实验舱完成转位操作,中国空
间站“”字基本构型在轨组装完成,空间站运行周期约为90分钟。北斗系统的 卫星
是地球静止轨道卫星,空间站和 卫星绕地球的运动均可视为匀速圆周运动,下列说
法正确的是( )
C
A. 卫星可以在地面任何一点的正上方,但离地心的距离是一定的
B.空间站的轨道半径比 卫星的轨道半径大
C.空间站的线速度比 卫星的线速度大
D.空间站的向心加速度比 卫星的向心加速度小
【解析】 北斗系统的 卫星是地球静止轨道卫星,一定位于赤道正上方。
由开普勒第三定律可得,空间站的轨道半径比 卫星的轨道半径小。
由万有引力提供向心力有,则, ,故空间站
的线速度比 卫星的线速度大(【大招运用】本题也可以运用大招“高轨低速大周期”
进行快速解答,空间站的运动周期小,则空间站对应的是“低轨高速小周期”。),空间
站的向心加速度比 卫星的向心加速度大。
. .
. .
跳跳学长 敲黑板
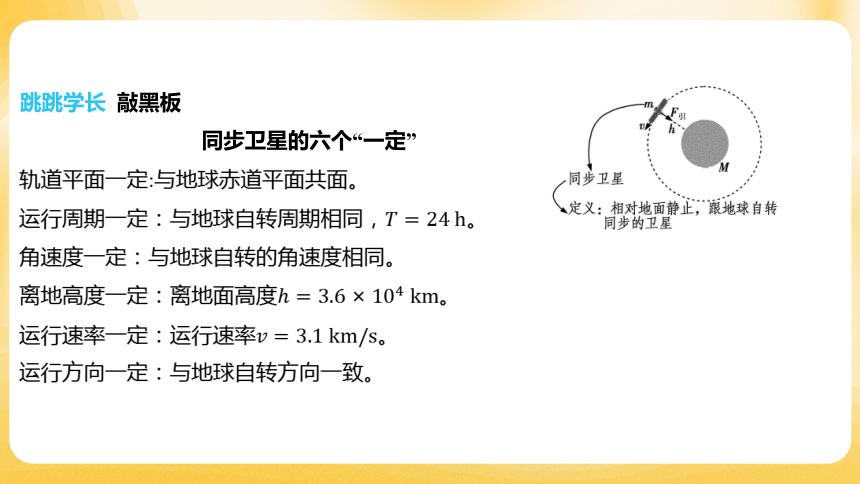
同步卫星的六个“一定”
轨道平面一定:与地球赤道平面共面。
运行周期一定:与地球自转周期相同, 。
角速度一定:与地球自转的角速度相同。
离地高度一定:离地面高度 。
运行速率一定:运行速率 。
运行方向一定:与地球自转方向一致。
4.(2024湖南名校联考联合体联考)有、、、四颗地球卫星: 还未发射,在地球
赤道上随地球表面一起转动,在地球的近地圆轨道上正常运行,是地球同步卫星,
是高空探测卫星。各卫星排列位置如图,则下列说法正确的是( )
C
A.的向心加速度大于 的向心加速度
B.四颗卫星的线速度大小关系是
C.在相同时间内 转过的弧长最长
D.的运动周期可能是
【解析】 因为、的角速度相同,离地心的距离小于 离地心的距离,根据
可知,的向心加速度小于的向心加速度;、 是围绕地球公转的卫星,根据
万有引力提供向心力有,解得,因的轨道半径小于 的轨道半径,所
以的向心加速度大于的向心加速度,综上分析可知,的向心加速度小于 的向心加
速度(【点拨】是地球同步卫星,可将 作为中介进行比较。)。
因为、的角速度相同,根据可知,的线速度小于的;、、 是围绕地
球公转的卫星,根据万有引力提供向心力有,解得,因 的轨道半
径最小,的轨道半径最大,所以的线速度大于的线速度,的线速度大于 的线速度
(【大招应用】根据大招中的口诀“高轨低速大周期”可得 。),则
, 。
. .
. .
. .
. .
因的线速度最大,则在相同时间内 转过的弧长最长。
、是围绕地球公转的卫星,根据万有引力提供向心力有 ,解得
,因的轨道半径大于的轨道半径,则的运动周期大于的运动周期,而
的运动周期是,则的运动周期大于 。
考点3 卫星变轨与对接问题
大招34 对应练习
解题觉醒
1.题型特征
(1)出现变轨轨道(椭圆)。
(2)卫星分别处在轨道各点,定性比较速度、加速度等。
(1)速度大小比较:①两圆轨道速度比较,用口诀“高轨低速大周期”即可。②一个圆
轨道一个椭圆轨道比较,用加速离心、减速向心分析。
(2)加速度大小比较: ,而万有引力大小与卫星离中心天体的距离有关。
(3)周期比较:用口诀“高轨低速大周期”分析,椭圆轨道的高度取半长轴即可。
2.解题技巧
5.(2025山西运城开学考)如图所示,月球探测器由
地面发射后,进入地月转移轨道,经过 点时变轨进
入圆形轨道1,在轨道1上经过 点时变轨进入椭圆轨
道2,轨道2与月球表面相切于点,探测器在 点着
陆月球。下列说法正确的是( )
D
A.月球的第一宇宙速度小于探测器在轨道1上的速度
B.探测器在轨道1上经过 点的速度大于在地月转移轨
道上经过 点的速度
C.探测器在轨道1上的运动周期小于在轨道2上的周期
D.探测器在轨道1上经过 点时的加速度等于在轨道2
上经过 点时的加速度
【解析】 月球的第一宇宙速度等于近月轨道的环绕速度,根据 ,解得
,由于轨道1的半径大于近月卫星的轨道半径,则月球的第一宇宙速度大于探
测器在轨道1上的速度。
由地月转移轨道变轨到轨道1是由高轨道变轨到低轨道,需要在两轨道切点 位置
减速,则探测器在轨道1上经过点的速度小于在地月转移轨道上经过 点的速度。
根据开普勒第三定律可知 ,由于轨道1的半径大于轨道2的半长轴(【点拨】
轨道1的直径大于轨道2的长轴。),则探测器在轨道1上的运动周期大于在轨道2上的周
期。
根据,解得 ,卫星在同一点与月心间距相等,加速度大小相等,
即探测器在轨道1上经过点时的加速度大小等于在轨道2上经过 点时的加速度。
【大招运用】“高轨低速大周期”,椭圆轨道与圆轨道相比时,取椭圆轨道的半长轴,轨
道1的半径大于轨道2的半长轴,可知探测器在轨道1上的运动周期比在轨道2上的大,C
错误。“比加速度,只看高度”,可知探测器在轨道1上经过 点时的加速度大小等于在轨
道2上经过 点时的加速度,D正确。
6.(2025北京朝阳区阶段练习)太空碎片会对航天器带来危害。设空间站在地球附近沿
逆时针方向做匀速圆周运动,如图中实线所示。为了避开碎片,空间站在 点向图中箭
头所指径向方向极短时间喷射气体,使空间站获得一定的反冲速度,从而实现变轨。变
轨后的轨道如图中虚线所示,其半长轴大于原轨道半径。则 ( )
D
A.空间站变轨前、后在 点的加速度不相等
B.空间站变轨后的运动周期比变轨前的小
C.空间站变轨后在 点的速度比变轨前的小
D.空间站变轨前的速度比变轨后在近地点的小
【解析】 在 点变轨前、后空间站受到的万有引力不变,根据牛顿第二定律可知,
空间站变轨前、后在 点的加速度相等。
因为变轨后轨道半长轴大于原轨道半径,根据开普勒第三定律可知,空间站变轨
后的运动周期比变轨前的大。
【大招运用】根据大招中比较加速度的方法可知,空间站变轨前、后在 点的加速度相
等,A错误。根据大招中比较周期的方法,由变轨后轨道半长轴大于原轨道半径可知,
空间站变轨后的运动周期比变轨前的大,B错误。
变轨后空间站在 点因反冲运动相当于极短时间获得竖直向下的速度,原水平向左
的圆周运动速度不变,因此合速度变大,即空间站变轨后在 点的速度比变轨前的大。
由于空间站变轨后在 点的速度比变轨前大,又根据开普勒第二定律可知,变轨后
在 点的速度比在近地点的速度小,则空间站变轨前的速度比变轨后在近地点的小。
7.[多选](2024河南部分名校模拟)如图所示,质量为的“天问一号”探测器在 点
制动后成功进入长轴为、短轴为 的椭圆轨道,椭圆轨道的半长轴等于火星的直径
,探测器在椭圆轨道上环绕数圈后,在近火点 (接近火星表面)再次制动并顺利进
入近火圆轨道。已知火星表面的重力加速度大小为,椭圆轨道上、 两点的曲率半径
均为,椭圆的面积 ,忽略火星的自转及探测器变轨时质量的变化,下列说法
正确的是( )
A.椭圆轨道围成的面积为
B.探测器在点制动后的动能为
C.探测器在点制动前的动能为
D.探测器在点变轨时克服发动机做的功为
ACD
【解析】 如图所示,火星位于椭圆轨道的一个焦点上,
根据几何关系可知,椭圆轨道的半短轴
,所以椭圆轨道围成的面积为
。
椭圆轨道上、两点的曲率半径 ,在椭圆上
的点有,,解得 。
在椭圆上的点有,,解得 。
探测器在近火轨道上的动能,根据动能定理知,探测器在 点变轨时,发
动机对探测器做的功 。
8.设问新颖(2023辽宁葫芦岛一模)2022年11月12日12时10分,“天舟五号”与空间站“天
和”核心舱成功对接(如图),此次发射任务从点火发射到完成交会对接,全程仅用2个
小时,创世界最快交会对接纪录,标志着我国航天交会对接技术取得了新突破。在交会
对接的最后阶段,“天舟五号”与空间站处于同一轨道上同向运动,两者的运行轨道均视
为圆周。要使“天舟五号”在同一轨道上追上空间站实现对接,“天舟五号”喷射燃气的方
向可能正确的是( )
A. B.
C. D.
【解析】 要想使“天舟五号”与空间站在同一轨道上对接,则需要使“天舟五号”加
速,与此同时要想不脱离原轨道,根据 可知,必须要增加向心力,即喷气时产
生的推力不仅要有沿轨道向前的分量,还要有指向地心的分量,由相互作用力可知,喷
气产生的推力方向与“天舟五号”喷射燃气方向相反。
√
觉醒集训
1.(2024广西师范大学附属中学模拟)2024年3月11日迎来“二月二,龙抬头”。“龙”指的
是二十八宿中的东方苍龙七宿星象,每岁仲春卯月之初,“龙角星”就从东方地平线上升
起,故称“龙抬头”。10点后朝东北方天空看去,有两颗亮星“角宿一”和“角宿二”,就是
龙角星。该龙角星可视为双星系统,系统内两颗恒星距离只有( 为天文单
位),公转周期只有4.0145天。根据以上信息以及引力常量 ,
下列说法正确的是( )
B
A.可以求出系统内两恒星的质量比 B.可以求出系统内两恒星的总质量
C.可以求出系统内两恒星的自转角速度 D.可以求出系统内两恒星的公转速率
【解析】 设两恒星质量分别为和,轨道半径分别为和,有 ,
,又,,联立可得 ,根据线速度与角
速度的关系,,得 ,综上可知:不可以求
出系统内两恒星的质量比,可以求出系统内两恒星的总质量,不可以求出系统内两恒星
的自转角速度,不可以求出系统内两恒星的公转速率。
2.(2025四川一模)已知、 两颗卫星为赤道平面的中圆地球
轨道卫星,绕行方向均与地球自转方向一致, 为地心,如图
所示。、两卫星的轨道半径之比为,卫星 的运行周期
为,图示时刻,卫星与卫星 相距最近。则下列说法正确的
是( )
D
A.卫星的运行周期为
B.经过时间,卫星与卫星 又一次相距最近
C.卫星 的发射速度小于第一宇宙速度
D.、分别与地心连线在相等时间内扫过的面积之比为
【解析】 卫星绕地球做圆周运动,万有引力提供向心力,则有
,解得,,设卫星、 的运行周期分别为
、,其中,则,所以 。
设经过时间,卫星与卫星又一次相距最近,则有 ,由A选项
可知,,解得 。
第一宇宙速度是最小发射速度,则卫星 的发射速度大于第一宇宙速度。
由A选项可知,则卫星在时间内扫过的面积为 ,
所以、分别与地心连线在相等时间内扫过的面积之比为 。
3.(2025湖北襄阳五中开学考)同一“探测卫星”分别围绕某星球和地球多次做圆周运动。
“探测卫星”在圆周运动中周期的二次方与轨道半径三次方 的关系图像如图所示,其
中表示“探测卫星”绕该星球运动的关系图像, 表示“探测卫星”绕地球运动的关系图
像,“探测卫星”在该星球近表面和地球近表面运动时均满足,图中、、 已知,
则( )
C
A.该星球和地球的密度之比为
B.该星球和地球的密度之比为
C.该星球和地球的第一宇宙速度之比为
D.该星球和地球的第一宇宙速度之比为
【解析】 设“探测卫星”的质量为,该星球的质量为,地球的质量为 ,
当“探测卫星”在该星球近表面做圆周运动时,有 ,当“探测卫星”在地
球近表面做圆周运动时,有,联立可得,又 ,则
星球的密度为,地球的密度为,所以 。
当“探测卫星”在该星球近表面运动时,轨道半径为星球半径 ,此时
,可得,当“探测卫星”在地球近表面运动时 ,轨道半径为地球半
径,此时 ,可得【点拨】此处的关键点是由图像求出中心天体的半径。
。根据万有引力提供向心力有,可得 ,所以星球的第一宇
宙速度为,地球的第一宇宙速度为 ,所以
。
4.(2023广东卷)如图甲所示,太阳系外的一颗行星绕恒星做匀速圆周运动。由于
的遮挡,探测器探测到的亮度随时间做如图乙所示的周期性变化,该周期与 的公转
周期相同。已知的质量为,引力常量为。关于 的公转,下列说法正确的是( )
B
A.周期为 B.半径为
C.角速度的大小为 D.加速度的大小为
【解析】 由题图乙可知,探测器探测到的亮度随时间变化的周期 ,
则的公转周期 。
绕恒星做匀速圆周运动,由万有引力提供向心力可得 ,解得半径
。
的角速度大小 。
的加速度大小 。
5.[多选](2025广西贵港阶段练习)如图所示,一颗质量为 的卫星要发射到中地圆
轨道上,通过、 两位置的变轨,经椭圆转移轨道进入中地圆轨道运行。已知近地圆
轨道的半径可认为等于地球半径,中地圆轨道与近地圆轨道共平面且轨道半径为地球半
径的3倍,地球半径为,地球表面的重力加速度为 ,下列说法正确的是( )
A.卫星进入中地圆轨道时需要在 点减速
B.卫星在转移轨道上的点和点速度大小关系为
C.该卫星在中地圆轨道上运行的速度大小为
D.该卫星在转移轨道上从点运行至点(、 与地心在同一直线上)所需的时间为
√
√
【解析】 卫星进入中地圆轨道时需要在 点加速。
根据开普勒第二定律可知,根据题意有 ,则
(【点拨】此处的关键点是利用微元法,取一段极短的时间,则在该时间内
卫星通过的轨迹可看成一段直线,卫星与地心扫过的形状可看成三角形。)。
卫星在中地圆轨道上,由万有引力提供向心力得 ,在地面有
,解得 。
卫星在中地圆轨道上的周期 ,根据几何关系可知,转移轨道的
半长轴为,由开普勒第三定律得,联立解得 ,在转移轨道上
从点运行至点所需的时间 。
. .
. .
6.(2024山东省实验中学模拟)中国科幻大片《流浪地球2》中描述的“太空电梯”让人
印象深刻,由教育部深空探测联合研究中心组织、重庆大学等高校合作的“多段式多功
能载运月球天梯概念研究”原理与其类似。图甲是“天梯”项目海基平台效果图,是在赤
道上建造垂直于水平面的“太空电梯”,航天员乘坐太空舱通过“太空电梯”直通地球空间
站。图乙中为航天员到地心的距离,为地球半径,曲线 为地球引力对航天员产生的
加速度大小与的关系;直线为航天员由于地球自转而产生的向心加速度大小与 的关
系,关于质量为 、相对地面静止在不同高度的航天员,下列说法正确的是( )
A.随着 的增大,航天员的角速度减小
B.随着 的增大,航天员感受到的“重力”先增
大后减小
C.航天员随地球自转的周期为
D.在离地面高为 的位置,航天员对座椅的压
力大小为
√
【解析】 航天员的角速度与地球自转角速度相等,保持不变。
根据,得,由题图可知,随着
的增大,当, 逐渐减小,则航天员感受到的“重力”逐渐减小;当
, 逐渐反向增大,则航天员感受到的“重力”逐渐增大。
当时,有,航天员随地球自转的周期为 。
由题意得,又,得 ,根据牛
顿第三定律可知,航天员对座椅的压力大小为 。
7.(2025重庆巴蜀中学月考)如图所示,地球赤道上空有两颗在赤道平面内运行的卫星
甲、乙,其中甲为地球同步卫星,乙运行的轨道半径为地球半径 的2倍,运动方向与
地球自转方向相反,运行周期为 。在赤道某处有一位天文观测者与地面相对静止。已
知地球自转周期为,卫星甲对地球的最大观测视角为 ,若甲、乙之间无遮挡物时可
进行无线信号通信,则下列说法正确的是( )
C
A.卫星乙连续两次出现在观测者正上方的时间间隔为
B.卫星乙连续两次出现在观测者正上方的时间间隔为
C.甲、乙卫星间不能直接通信持续的最长时间是
D.甲、乙卫星间不能直接通信持续的最长时间是
【解析】 由于卫星乙运动方向与地球自转方向相反,所以圈数和等于1时卫
星乙再次出现在观测者正上方,则有,解得 。
卫星甲与地面上的 点同步,考虑甲与乙的相对运动,
如图所示,则有 ,解
得信号连续中断的最长时间为 。
觉醒原创
1.将没有地球遮挡时同一圆周轨道上两颗地球卫星之间
的距离称为视线距离。如图所示同一圆周轨道上的两
颗地球卫星、绕地球运动,点为地心。已知、
的周期为地球近地卫星周期的 倍,且卫星运行轨
道与赤道共面,地球的半径约为。则卫星 、
之间的最大视线距离约为( )
A
A. B. C. D.
【解析】 对近地卫星和卫星,由开普勒第三定律可知,可得卫星、 的
轨道半径为。由几何关系可知视线距离最大时,卫星、 连线与地球赤道相切,如
图所示,则由几何关系可得此时卫星、间距离为 。
2.[多选]2024年10月,中国科学院上海天文台葛健教授带领的国际团队首次利用人工
智能发现了5颗直径小于地球、轨道周期短于1天的超短周期行星。已知其中一颗超短周
期行星绕其主星做匀速圆周运动的周期为年, 绕其主星运
动的轨道半径与地球绕太阳运动的轨道半径的比值为, 的球体半径与地
球的球体半径的比值为 。下列说法正确的是( )
AD
A.绕其主星运动的线速度与地球绕太阳运动的线速度之比为
B.与地球的表面重力加速度之比为
C.主星与太阳的第一宇宙速度之比为
D.主星与太阳的质量之比为
【解析】 根据匀速圆周运动知识,可得 绕其主星运动的
线速度与地球绕太阳运动的线速度之比为 。
根据黄金代换公式,因无法知道 的质量,故无法得出表面
重力加速度与地球表面重力加速度的关系。
对绕中心天体表面做匀速圆周运动的行星,由万有引力提供向心力有
,可得中心天体质量为,则主星与太阳的质量之比为 。
根据第一宇宙速度公式 ,主星与太阳的质量之比可求,因无法知道主星与
太阳的球体半径的关系,故无法得出其第一宇宙速度与太阳的第一宇宙速度的关系。
3.[多选]2024年8月12日,中国科学院新疆天文台科研人员在使用中国天眼观测后发
现,脉冲星 处于罕见的双中子星系统中。该脉冲星的运行轨道为椭圆
轨道,脉冲星的伴星质量大于或等于太阳质量的1.28倍,是一颗中子星,系统总质量为
太阳质量的2.63倍。若将两星视为质量相等(均为 ),则互绕椭圆轨道如图甲所示,
均相当于仅受同一质量为的质心的引力做椭圆运动,图乙是质量均为的双星 、
的运行圆轨道,则( )
BC
A.若脉冲星逆时针转动,则伴星一定顺时针
转动
B.脉冲星、伴星与质心连线相同时间内扫过
的面积相等
C.脉冲星的运行周期等于行星 的运行周期
D.脉冲星在远星点的速度大于行星 的速度
【解析】 根据万有引力定律,双星系统运动过程两个星体的连线始终过质心,A错误。
两星轨道完全相同,由开普勒第二定律可知,B正确。根据开普勒第三定律 ,可
知围绕质量为的质心、以为半径做圆周运动的行星(质量为 ),其运动周期
与脉冲星运动周期相同,由万有引力定律可知 ,可知
,同理,对行星有,可得 ,综上可知脉冲星
的运行周期等于行星的运行周期,C正确。根据 易知,脉冲星在远星点的
速度小于行星的速度,又根据C选项可知, ,D错误。
专题五 万有引力与航天
考向二 宇宙航行问题
2025年高考物理专题复习资料
考点切片
考点1 宇宙速度
1.(2025山西吕梁开学考试)2024年5月8日,嫦娥六号探测器在北京航天飞行控制中心
的精确控制下,成功实施近月制动,顺利进入环月轨道飞行。嫦娥六号探测器的环月轨
道飞行可看成匀速圆周运动,运动周期为。已知月球质量与地球质量的比值为 ,月
球半径与地球半径的比值为,地球半径为,地球表面的重力加速度大小为 ,引力常
量为 ,则( )
B
A.嫦娥六号探测器发射的速度应大于第二宇宙速度小于第三宇宙速度
B.嫦娥六号探测器的环月轨道距月球表面的高度为
C.月球的第一宇宙速度大小为
D.月球表面的重力加速度大小为
【解析】 嫦娥六号探测器没有脱离地球引力,所以嫦娥六号探测器发射的速度应
大于第一宇宙速度小于第二宇宙速度。
在地球表面上有 ,嫦娥六号探测器环月做匀速圆周运动有
,联立解得 。
设月球的第一宇宙速度(【点拨】月球的第一宇宙速度等于近月卫星的线速度,是
环月卫星最大的环绕速度,也是在月球表面发射卫星的最小发射速度。)大小为 ,则有
,解得 。
在月球表面上有,解得 。
2.(2023湖南卷)根据宇宙大爆炸理论,密度较大区域的物质在万有引力作用下,不断
聚集可能形成恒星。恒星最终的归宿与其质量有关,如果质量为太阳质量的 倍将
坍缩成白矮星,质量为太阳质量的 倍将坍缩成中子星,质量更大的恒星将坍缩
成黑洞。设恒星坍缩前后可看成质量均匀分布的球体,质量不变,体积缩小,自转变快。
不考虑恒星与其他物体的相互作用。已知逃逸速度为第一宇宙速度的 倍,中子星密
度大于白矮星。根据万有引力理论,下列说法正确的是( )
B
A.同一恒星表面任意位置的重力加速度相同
B.恒星坍缩后表面两极处的重力加速度比坍缩前的大
C.恒星坍缩前后的第一宇宙速度不变
D.中子星的逃逸速度小于白矮星的逃逸速度
【解析】恒星自转万有引力有两个效果
从赤道到两极, , , 。
两极 , 。
第一宇宙速度 , 。
逃逸速度 。
跳跳学长 有话说
以质量均匀分布的地球为例,考虑地球的自
转,不同位置万有引力和重力的关系如图。
在一般位置,向心力和重力 的矢量和
构成万有引力 ;在两极位置,向心力为0,
万有引力等于重力,即 ,此处
重力加速度最大;在赤道位置,重力和向心力共线,即 ,此处重
力加速度最小。
考点2 近地卫星与同步卫星
3.科技强国(2024广东东莞阶段练习)2022年11月,梦天实验舱完成转位操作,中国空
间站“”字基本构型在轨组装完成,空间站运行周期约为90分钟。北斗系统的 卫星
是地球静止轨道卫星,空间站和 卫星绕地球的运动均可视为匀速圆周运动,下列说
法正确的是( )
C
A. 卫星可以在地面任何一点的正上方,但离地心的距离是一定的
B.空间站的轨道半径比 卫星的轨道半径大
C.空间站的线速度比 卫星的线速度大
D.空间站的向心加速度比 卫星的向心加速度小
【解析】 北斗系统的 卫星是地球静止轨道卫星,一定位于赤道正上方。
由开普勒第三定律可得,空间站的轨道半径比 卫星的轨道半径小。
由万有引力提供向心力有,则, ,故空间站
的线速度比 卫星的线速度大(【大招运用】本题也可以运用大招“高轨低速大周期”
进行快速解答,空间站的运动周期小,则空间站对应的是“低轨高速小周期”。),空间
站的向心加速度比 卫星的向心加速度大。
. .
. .
跳跳学长 敲黑板
同步卫星的六个“一定”
轨道平面一定:与地球赤道平面共面。
运行周期一定:与地球自转周期相同, 。
角速度一定:与地球自转的角速度相同。
离地高度一定:离地面高度 。
运行速率一定:运行速率 。
运行方向一定:与地球自转方向一致。
4.(2024湖南名校联考联合体联考)有、、、四颗地球卫星: 还未发射,在地球
赤道上随地球表面一起转动,在地球的近地圆轨道上正常运行,是地球同步卫星,
是高空探测卫星。各卫星排列位置如图,则下列说法正确的是( )
C
A.的向心加速度大于 的向心加速度
B.四颗卫星的线速度大小关系是
C.在相同时间内 转过的弧长最长
D.的运动周期可能是
【解析】 因为、的角速度相同,离地心的距离小于 离地心的距离,根据
可知,的向心加速度小于的向心加速度;、 是围绕地球公转的卫星,根据
万有引力提供向心力有,解得,因的轨道半径小于 的轨道半径,所
以的向心加速度大于的向心加速度,综上分析可知,的向心加速度小于 的向心加
速度(【点拨】是地球同步卫星,可将 作为中介进行比较。)。
因为、的角速度相同,根据可知,的线速度小于的;、、 是围绕地
球公转的卫星,根据万有引力提供向心力有,解得,因 的轨道半
径最小,的轨道半径最大,所以的线速度大于的线速度,的线速度大于 的线速度
(【大招应用】根据大招中的口诀“高轨低速大周期”可得 。),则
, 。
. .
. .
. .
. .
因的线速度最大,则在相同时间内 转过的弧长最长。
、是围绕地球公转的卫星,根据万有引力提供向心力有 ,解得
,因的轨道半径大于的轨道半径,则的运动周期大于的运动周期,而
的运动周期是,则的运动周期大于 。
考点3 卫星变轨与对接问题
大招34 对应练习
解题觉醒
1.题型特征
(1)出现变轨轨道(椭圆)。
(2)卫星分别处在轨道各点,定性比较速度、加速度等。
(1)速度大小比较:①两圆轨道速度比较,用口诀“高轨低速大周期”即可。②一个圆
轨道一个椭圆轨道比较,用加速离心、减速向心分析。
(2)加速度大小比较: ,而万有引力大小与卫星离中心天体的距离有关。
(3)周期比较:用口诀“高轨低速大周期”分析,椭圆轨道的高度取半长轴即可。
2.解题技巧
5.(2025山西运城开学考)如图所示,月球探测器由
地面发射后,进入地月转移轨道,经过 点时变轨进
入圆形轨道1,在轨道1上经过 点时变轨进入椭圆轨
道2,轨道2与月球表面相切于点,探测器在 点着
陆月球。下列说法正确的是( )
D
A.月球的第一宇宙速度小于探测器在轨道1上的速度
B.探测器在轨道1上经过 点的速度大于在地月转移轨
道上经过 点的速度
C.探测器在轨道1上的运动周期小于在轨道2上的周期
D.探测器在轨道1上经过 点时的加速度等于在轨道2
上经过 点时的加速度
【解析】 月球的第一宇宙速度等于近月轨道的环绕速度,根据 ,解得
,由于轨道1的半径大于近月卫星的轨道半径,则月球的第一宇宙速度大于探
测器在轨道1上的速度。
由地月转移轨道变轨到轨道1是由高轨道变轨到低轨道,需要在两轨道切点 位置
减速,则探测器在轨道1上经过点的速度小于在地月转移轨道上经过 点的速度。
根据开普勒第三定律可知 ,由于轨道1的半径大于轨道2的半长轴(【点拨】
轨道1的直径大于轨道2的长轴。),则探测器在轨道1上的运动周期大于在轨道2上的周
期。
根据,解得 ,卫星在同一点与月心间距相等,加速度大小相等,
即探测器在轨道1上经过点时的加速度大小等于在轨道2上经过 点时的加速度。
【大招运用】“高轨低速大周期”,椭圆轨道与圆轨道相比时,取椭圆轨道的半长轴,轨
道1的半径大于轨道2的半长轴,可知探测器在轨道1上的运动周期比在轨道2上的大,C
错误。“比加速度,只看高度”,可知探测器在轨道1上经过 点时的加速度大小等于在轨
道2上经过 点时的加速度,D正确。
6.(2025北京朝阳区阶段练习)太空碎片会对航天器带来危害。设空间站在地球附近沿
逆时针方向做匀速圆周运动,如图中实线所示。为了避开碎片,空间站在 点向图中箭
头所指径向方向极短时间喷射气体,使空间站获得一定的反冲速度,从而实现变轨。变
轨后的轨道如图中虚线所示,其半长轴大于原轨道半径。则 ( )
D
A.空间站变轨前、后在 点的加速度不相等
B.空间站变轨后的运动周期比变轨前的小
C.空间站变轨后在 点的速度比变轨前的小
D.空间站变轨前的速度比变轨后在近地点的小
【解析】 在 点变轨前、后空间站受到的万有引力不变,根据牛顿第二定律可知,
空间站变轨前、后在 点的加速度相等。
因为变轨后轨道半长轴大于原轨道半径,根据开普勒第三定律可知,空间站变轨
后的运动周期比变轨前的大。
【大招运用】根据大招中比较加速度的方法可知,空间站变轨前、后在 点的加速度相
等,A错误。根据大招中比较周期的方法,由变轨后轨道半长轴大于原轨道半径可知,
空间站变轨后的运动周期比变轨前的大,B错误。
变轨后空间站在 点因反冲运动相当于极短时间获得竖直向下的速度,原水平向左
的圆周运动速度不变,因此合速度变大,即空间站变轨后在 点的速度比变轨前的大。
由于空间站变轨后在 点的速度比变轨前大,又根据开普勒第二定律可知,变轨后
在 点的速度比在近地点的速度小,则空间站变轨前的速度比变轨后在近地点的小。
7.[多选](2024河南部分名校模拟)如图所示,质量为的“天问一号”探测器在 点
制动后成功进入长轴为、短轴为 的椭圆轨道,椭圆轨道的半长轴等于火星的直径
,探测器在椭圆轨道上环绕数圈后,在近火点 (接近火星表面)再次制动并顺利进
入近火圆轨道。已知火星表面的重力加速度大小为,椭圆轨道上、 两点的曲率半径
均为,椭圆的面积 ,忽略火星的自转及探测器变轨时质量的变化,下列说法
正确的是( )
A.椭圆轨道围成的面积为
B.探测器在点制动后的动能为
C.探测器在点制动前的动能为
D.探测器在点变轨时克服发动机做的功为
ACD
【解析】 如图所示,火星位于椭圆轨道的一个焦点上,
根据几何关系可知,椭圆轨道的半短轴
,所以椭圆轨道围成的面积为
。
椭圆轨道上、两点的曲率半径 ,在椭圆上
的点有,,解得 。
在椭圆上的点有,,解得 。
探测器在近火轨道上的动能,根据动能定理知,探测器在 点变轨时,发
动机对探测器做的功 。
8.设问新颖(2023辽宁葫芦岛一模)2022年11月12日12时10分,“天舟五号”与空间站“天
和”核心舱成功对接(如图),此次发射任务从点火发射到完成交会对接,全程仅用2个
小时,创世界最快交会对接纪录,标志着我国航天交会对接技术取得了新突破。在交会
对接的最后阶段,“天舟五号”与空间站处于同一轨道上同向运动,两者的运行轨道均视
为圆周。要使“天舟五号”在同一轨道上追上空间站实现对接,“天舟五号”喷射燃气的方
向可能正确的是( )
A. B.
C. D.
【解析】 要想使“天舟五号”与空间站在同一轨道上对接,则需要使“天舟五号”加
速,与此同时要想不脱离原轨道,根据 可知,必须要增加向心力,即喷气时产
生的推力不仅要有沿轨道向前的分量,还要有指向地心的分量,由相互作用力可知,喷
气产生的推力方向与“天舟五号”喷射燃气方向相反。
√
觉醒集训
1.(2024广西师范大学附属中学模拟)2024年3月11日迎来“二月二,龙抬头”。“龙”指的
是二十八宿中的东方苍龙七宿星象,每岁仲春卯月之初,“龙角星”就从东方地平线上升
起,故称“龙抬头”。10点后朝东北方天空看去,有两颗亮星“角宿一”和“角宿二”,就是
龙角星。该龙角星可视为双星系统,系统内两颗恒星距离只有( 为天文单
位),公转周期只有4.0145天。根据以上信息以及引力常量 ,
下列说法正确的是( )
B
A.可以求出系统内两恒星的质量比 B.可以求出系统内两恒星的总质量
C.可以求出系统内两恒星的自转角速度 D.可以求出系统内两恒星的公转速率
【解析】 设两恒星质量分别为和,轨道半径分别为和,有 ,
,又,,联立可得 ,根据线速度与角
速度的关系,,得 ,综上可知:不可以求
出系统内两恒星的质量比,可以求出系统内两恒星的总质量,不可以求出系统内两恒星
的自转角速度,不可以求出系统内两恒星的公转速率。
2.(2025四川一模)已知、 两颗卫星为赤道平面的中圆地球
轨道卫星,绕行方向均与地球自转方向一致, 为地心,如图
所示。、两卫星的轨道半径之比为,卫星 的运行周期
为,图示时刻,卫星与卫星 相距最近。则下列说法正确的
是( )
D
A.卫星的运行周期为
B.经过时间,卫星与卫星 又一次相距最近
C.卫星 的发射速度小于第一宇宙速度
D.、分别与地心连线在相等时间内扫过的面积之比为
【解析】 卫星绕地球做圆周运动,万有引力提供向心力,则有
,解得,,设卫星、 的运行周期分别为
、,其中,则,所以 。
设经过时间,卫星与卫星又一次相距最近,则有 ,由A选项
可知,,解得 。
第一宇宙速度是最小发射速度,则卫星 的发射速度大于第一宇宙速度。
由A选项可知,则卫星在时间内扫过的面积为 ,
所以、分别与地心连线在相等时间内扫过的面积之比为 。
3.(2025湖北襄阳五中开学考)同一“探测卫星”分别围绕某星球和地球多次做圆周运动。
“探测卫星”在圆周运动中周期的二次方与轨道半径三次方 的关系图像如图所示,其
中表示“探测卫星”绕该星球运动的关系图像, 表示“探测卫星”绕地球运动的关系图
像,“探测卫星”在该星球近表面和地球近表面运动时均满足,图中、、 已知,
则( )
C
A.该星球和地球的密度之比为
B.该星球和地球的密度之比为
C.该星球和地球的第一宇宙速度之比为
D.该星球和地球的第一宇宙速度之比为
【解析】 设“探测卫星”的质量为,该星球的质量为,地球的质量为 ,
当“探测卫星”在该星球近表面做圆周运动时,有 ,当“探测卫星”在地
球近表面做圆周运动时,有,联立可得,又 ,则
星球的密度为,地球的密度为,所以 。
当“探测卫星”在该星球近表面运动时,轨道半径为星球半径 ,此时
,可得,当“探测卫星”在地球近表面运动时 ,轨道半径为地球半
径,此时 ,可得【点拨】此处的关键点是由图像求出中心天体的半径。
。根据万有引力提供向心力有,可得 ,所以星球的第一宇
宙速度为,地球的第一宇宙速度为 ,所以
。
4.(2023广东卷)如图甲所示,太阳系外的一颗行星绕恒星做匀速圆周运动。由于
的遮挡,探测器探测到的亮度随时间做如图乙所示的周期性变化,该周期与 的公转
周期相同。已知的质量为,引力常量为。关于 的公转,下列说法正确的是( )
B
A.周期为 B.半径为
C.角速度的大小为 D.加速度的大小为
【解析】 由题图乙可知,探测器探测到的亮度随时间变化的周期 ,
则的公转周期 。
绕恒星做匀速圆周运动,由万有引力提供向心力可得 ,解得半径
。
的角速度大小 。
的加速度大小 。
5.[多选](2025广西贵港阶段练习)如图所示,一颗质量为 的卫星要发射到中地圆
轨道上,通过、 两位置的变轨,经椭圆转移轨道进入中地圆轨道运行。已知近地圆
轨道的半径可认为等于地球半径,中地圆轨道与近地圆轨道共平面且轨道半径为地球半
径的3倍,地球半径为,地球表面的重力加速度为 ,下列说法正确的是( )
A.卫星进入中地圆轨道时需要在 点减速
B.卫星在转移轨道上的点和点速度大小关系为
C.该卫星在中地圆轨道上运行的速度大小为
D.该卫星在转移轨道上从点运行至点(、 与地心在同一直线上)所需的时间为
√
√
【解析】 卫星进入中地圆轨道时需要在 点加速。
根据开普勒第二定律可知,根据题意有 ,则
(【点拨】此处的关键点是利用微元法,取一段极短的时间,则在该时间内
卫星通过的轨迹可看成一段直线,卫星与地心扫过的形状可看成三角形。)。
卫星在中地圆轨道上,由万有引力提供向心力得 ,在地面有
,解得 。
卫星在中地圆轨道上的周期 ,根据几何关系可知,转移轨道的
半长轴为,由开普勒第三定律得,联立解得 ,在转移轨道上
从点运行至点所需的时间 。
. .
. .
6.(2024山东省实验中学模拟)中国科幻大片《流浪地球2》中描述的“太空电梯”让人
印象深刻,由教育部深空探测联合研究中心组织、重庆大学等高校合作的“多段式多功
能载运月球天梯概念研究”原理与其类似。图甲是“天梯”项目海基平台效果图,是在赤
道上建造垂直于水平面的“太空电梯”,航天员乘坐太空舱通过“太空电梯”直通地球空间
站。图乙中为航天员到地心的距离,为地球半径,曲线 为地球引力对航天员产生的
加速度大小与的关系;直线为航天员由于地球自转而产生的向心加速度大小与 的关
系,关于质量为 、相对地面静止在不同高度的航天员,下列说法正确的是( )
A.随着 的增大,航天员的角速度减小
B.随着 的增大,航天员感受到的“重力”先增
大后减小
C.航天员随地球自转的周期为
D.在离地面高为 的位置,航天员对座椅的压
力大小为
√
【解析】 航天员的角速度与地球自转角速度相等,保持不变。
根据,得,由题图可知,随着
的增大,当, 逐渐减小,则航天员感受到的“重力”逐渐减小;当
, 逐渐反向增大,则航天员感受到的“重力”逐渐增大。
当时,有,航天员随地球自转的周期为 。
由题意得,又,得 ,根据牛
顿第三定律可知,航天员对座椅的压力大小为 。
7.(2025重庆巴蜀中学月考)如图所示,地球赤道上空有两颗在赤道平面内运行的卫星
甲、乙,其中甲为地球同步卫星,乙运行的轨道半径为地球半径 的2倍,运动方向与
地球自转方向相反,运行周期为 。在赤道某处有一位天文观测者与地面相对静止。已
知地球自转周期为,卫星甲对地球的最大观测视角为 ,若甲、乙之间无遮挡物时可
进行无线信号通信,则下列说法正确的是( )
C
A.卫星乙连续两次出现在观测者正上方的时间间隔为
B.卫星乙连续两次出现在观测者正上方的时间间隔为
C.甲、乙卫星间不能直接通信持续的最长时间是
D.甲、乙卫星间不能直接通信持续的最长时间是
【解析】 由于卫星乙运动方向与地球自转方向相反,所以圈数和等于1时卫
星乙再次出现在观测者正上方,则有,解得 。
卫星甲与地面上的 点同步,考虑甲与乙的相对运动,
如图所示,则有 ,解
得信号连续中断的最长时间为 。
觉醒原创
1.将没有地球遮挡时同一圆周轨道上两颗地球卫星之间
的距离称为视线距离。如图所示同一圆周轨道上的两
颗地球卫星、绕地球运动,点为地心。已知、
的周期为地球近地卫星周期的 倍,且卫星运行轨
道与赤道共面,地球的半径约为。则卫星 、
之间的最大视线距离约为( )
A
A. B. C. D.
【解析】 对近地卫星和卫星,由开普勒第三定律可知,可得卫星、 的
轨道半径为。由几何关系可知视线距离最大时,卫星、 连线与地球赤道相切,如
图所示,则由几何关系可得此时卫星、间距离为 。
2.[多选]2024年10月,中国科学院上海天文台葛健教授带领的国际团队首次利用人工
智能发现了5颗直径小于地球、轨道周期短于1天的超短周期行星。已知其中一颗超短周
期行星绕其主星做匀速圆周运动的周期为年, 绕其主星运
动的轨道半径与地球绕太阳运动的轨道半径的比值为, 的球体半径与地
球的球体半径的比值为 。下列说法正确的是( )
AD
A.绕其主星运动的线速度与地球绕太阳运动的线速度之比为
B.与地球的表面重力加速度之比为
C.主星与太阳的第一宇宙速度之比为
D.主星与太阳的质量之比为
【解析】 根据匀速圆周运动知识,可得 绕其主星运动的
线速度与地球绕太阳运动的线速度之比为 。
根据黄金代换公式,因无法知道 的质量,故无法得出表面
重力加速度与地球表面重力加速度的关系。
对绕中心天体表面做匀速圆周运动的行星,由万有引力提供向心力有
,可得中心天体质量为,则主星与太阳的质量之比为 。
根据第一宇宙速度公式 ,主星与太阳的质量之比可求,因无法知道主星与
太阳的球体半径的关系,故无法得出其第一宇宙速度与太阳的第一宇宙速度的关系。
3.[多选]2024年8月12日,中国科学院新疆天文台科研人员在使用中国天眼观测后发
现,脉冲星 处于罕见的双中子星系统中。该脉冲星的运行轨道为椭圆
轨道,脉冲星的伴星质量大于或等于太阳质量的1.28倍,是一颗中子星,系统总质量为
太阳质量的2.63倍。若将两星视为质量相等(均为 ),则互绕椭圆轨道如图甲所示,
均相当于仅受同一质量为的质心的引力做椭圆运动,图乙是质量均为的双星 、
的运行圆轨道,则( )
BC
A.若脉冲星逆时针转动,则伴星一定顺时针
转动
B.脉冲星、伴星与质心连线相同时间内扫过
的面积相等
C.脉冲星的运行周期等于行星 的运行周期
D.脉冲星在远星点的速度大于行星 的速度
【解析】 根据万有引力定律,双星系统运动过程两个星体的连线始终过质心,A错误。
两星轨道完全相同,由开普勒第二定律可知,B正确。根据开普勒第三定律 ,可
知围绕质量为的质心、以为半径做圆周运动的行星(质量为 ),其运动周期
与脉冲星运动周期相同,由万有引力定律可知 ,可知
,同理,对行星有,可得 ,综上可知脉冲星
的运行周期等于行星的运行周期,C正确。根据 易知,脉冲星在远星点的
速度小于行星的速度,又根据C选项可知, ,D错误。
同课章节目录
