考向二 动能定理及其应用-2025年高考物理专题复习课件
文档属性
| 名称 | 考向二 动能定理及其应用-2025年高考物理专题复习课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-02-18 09:45:54 | ||
图片预览










文档简介
(共34张PPT)
专题六 功和能
考向二 动能定理及其应用
2025年高考物理专题复习资料
考点切片
考点1 对动能定理的理解
解题觉醒
1.题型特征:应用动能定理求解相关物理量。
2.解题技巧
(1)多过程问题,优先对全程列动能定理方程;
(2)求时间,首选牛顿第二定律
3.解题步骤
(1)找出做功的力;
(2)计算动能变化量;
(3)
1.(2025贵州六校联盟模拟)巴黎奥运会网球女单决赛中,中国选手郑钦文以 战胜
克罗地亚选手维基奇夺冠。这是中国运动员史上首次赢得奥运网球单打项目的金牌。某
次运动员将质量为的网球击出,网球被击出瞬间距离地面的高度为 ,网球的速度大
小为,经过一段时间网球落地,落地瞬间的速度大小为 ,假设网球被击前瞬间,速
度大小为0,重力加速度大小为,网球克服空气阻力做的功为 。则下列说法正确的
是( )
D
A.击球过程,球拍对网球做的功为
B.网球从被击出到落地的过程,网球动能的增加量为
C.网球从被击出到落地的过程,网球的机械能减少
D.
【解析】 击球过程,根据动能定理有,即球拍对网球做的功为 。
网球从被击出到落地,根据动能定理有 。
根据功能关系可知,网球从被击出到落地,网球的机械能减少 。
根据动能定理有,解得 。
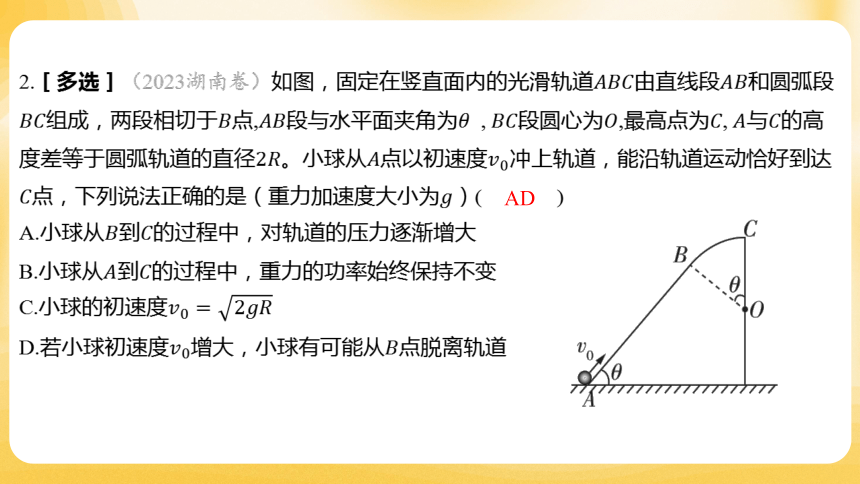
2.[多选](2023湖南卷)如图,固定在竖直面内的光滑轨道由直线段 和圆弧段
组成,两段相切于点,段与水平面夹角为 ,段圆心为,最高点为,与 的高
度差等于圆弧轨道的直径。小球从点以初速度 冲上轨道,能沿轨道运动恰好到达
点,下列说法正确的是(重力加速度大小为 )( )
AD
A.小球从到 的过程中,对轨道的压力逐渐增大
B.小球从到 的过程中,重力的功率始终保持不变
C.小球的初速度
D.若小球初速度增大,小球有可能从 点脱离轨道
【解析】 小球恰好运动至点,即小球在点速度 。
小球在圆弧上运动到 点的受力分析如图所示
小球从到 。
若小球在点的速度满足,则小球将从 点脱离轨道。
3.(2023重庆卷)机械臂广泛应用于机械装配。若某质量为 的
工件(视为质点)被机械臂抓取后,在竖直平面内由静止开始
斜向上做加速度大小为 的匀加速直线运动,运动方向与竖直方
向夹角为 ,提升高度为 ,如图所示。求:
(1) 提升高度为 时,工件的速度大小;
【答案】
【解析】 根据匀变速直线运动位移与速度关系有
解得 。
(2) 在此过程中,工件运动的时间及合力对工件做的功。
【答案】 ;
【解析】 根据速度—时间公式有
解得
根据动能定理有
解得 。
考点2 动能定理求解变力做功问题
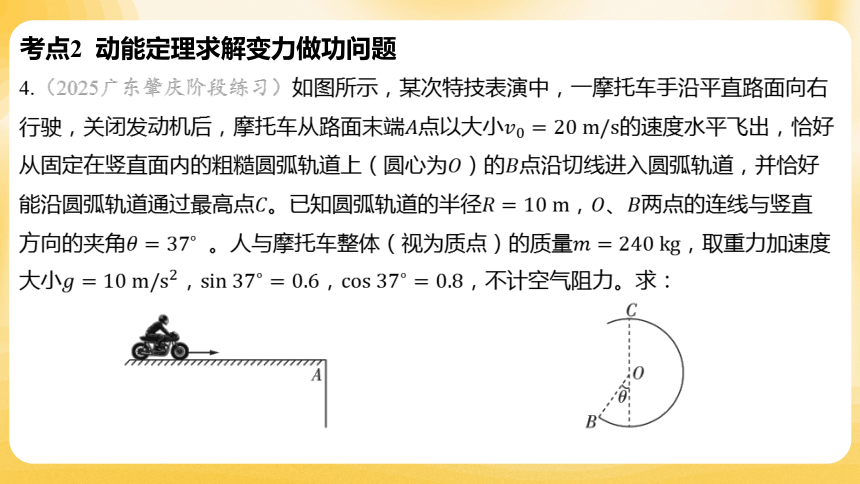
4.(2025广东肇庆阶段练习)如图所示,某次特技表演中,一摩托车手沿平直路面向右
行驶,关闭发动机后,摩托车从路面末端点以大小 的速度水平飞出,恰好
从固定在竖直面内的粗糙圆弧轨道上(圆心为)的 点沿切线进入圆弧轨道,并恰好
能沿圆弧轨道通过最高点。已知圆弧轨道的半径,、 两点的连线与竖直
方向的夹角 。人与摩托车整体(视为质点)的质量 ,取重力加速度
大小,, ,不计空气阻力。求:
(1) 、两点间的水平距离 ;
【答案】 30
【解析】 设整体通过点时的速度大小为,有
整体通过点时的竖直分速度大小
设整体从点运动到点的时间为,有
又
解得 。
(2) 整体从点运动到点的过程中,克服轨道阻力做的功 。
【答案】
【解析】 由(1)可得,设整体通过点时的速度大小为,有
对整体从点运动到 点的过程,由动能定理可得
解得 。
5.(2024上海市七宝中学月考)如图所示,水平圆盘边缘有一个物块
(可看作质点),现将圆盘由静止开始绕过圆心的竖直轴转动,缓慢
增大圆盘的角速度,当圆盘转动的角速度增大到某一数值时,物块恰
从圆盘边缘滑落。已知圆盘半径为,物块的质量为 ,物块与圆盘
间的动摩擦因数为 ,最大静摩擦力等于滑动摩擦力,水平圆盘与地
面的高度差为,重力加速度大小为 。求:
(1) 物块恰好滑离圆盘边缘的线速度 的大小;
【答案】
【解析】 物块恰好滑离圆盘时摩擦力达到最大静摩擦力,
由牛顿第二定律有
解得 。
(2) 圆盘从静止开始至物块滑离圆盘的过程,摩擦力对物块所做的功 ;
【答案】
【解析】 圆盘从静止开始至物块滑离圆盘过程中,
由动能定理有
可得 。
(3) 物块落地点到圆盘中心的水平距离 。
【答案】
【解析】 物块将沿着圆盘切线方向滑离圆盘做平抛运动,设物块落地时间为 ,做平抛
运动的水平位移为,则有,
解得
则可得物块落地点到圆盘中心的水平距离 。(【易错】容
易将平抛运动的水平位移 当成物块落地点到圆盘中心的水平距离。)
. .
考点3 动能定理求解竖直圆问题
解题觉醒
1.题型特征:小球在竖直圆中运动。
2.解题技巧:口诀“力径减半得动能”。公式 。
如图,小球质量为,做圆周运动的半径为,小球从到 过程摩
擦力做的功为 。
小球在点的动能为,小球在点的动能为 ,
根据动能定理得 。
6.(2024四川遂宁模拟)如图所示,一小球以一定的初速度从图示位置进入光滑的轨道,
小球先进入圆轨道1,再进入圆轨道2,圆轨道1的半径为 ,圆轨道2的半径是轨道1的
1.8倍,小球的质量为。若小球恰好能通过轨道2的最高点 ,则小球在轨道1上经过其
最高点时对轨道的压力大小为(重力加速度大小为 )( )
C
A. B. C. D.
【解析】 小球恰好能通过轨道2的最高点 ,运用大招口诀“力径减半得动能”(【提醒】
注意运用大招“力径减半得动能”公式时,若是选择题、填空题可直接写出,若是计算题
需要写出解答过程的,必须写出规范的动能定理公式,为了简化运算我们可以在草稿纸
上列大招公式进行代替。)得,小球从到 的过程,由动
能定理得,其中为小球在点的向心力,在 点由
牛顿第二定律得,解得 ,由牛顿第三定律可知小球在轨道1上经
过其最高点时对轨道的压力大小为 。
7.[多选](2024黑龙江双鸭山市一中模拟)如图所示,
在光滑的斜轨道底端平滑连接着一个半径为 、顶端有缺
口的光滑圆弧轨道,点、点在同一水平面上, 点是最
低点, 。一质量为 的小球由斜轨道上某高
度处静止释放,由轨道连接处进入圆弧轨道。重力加速度
BD
A.若小球滑到点时速度大小为,则此处轨道对小球作用力的大小为
B.若小球滑到点时速度大小为,则小球滑到点时速度大小为
C.若小球恰好能通过圆弧形轨道上点,则小球在斜轨道上静止释放的高度为
D.若小球从圆弧形轨道上点飞出后恰好从点飞入圆弧形轨道,则小球经过 点时的速
度大小为
大小为 ,不考虑机械能的损失,下列说法正确的是 ( )
【解析】 小球在点,根据牛顿第二定律有 ,则此处轨道对小球作
用力的大小为 。
小球从圆弧轨道最低点滑到 点,由动能定理有
,解得 。
若小球恰好能通过圆弧轨道内点,根据牛顿第二定律有 ,小球
从释放到点,根据动能定理有,解得 。
(【大招运用】根据大招内容中口诀“力径减半得动能”可知小球到达 点时的动能为
,由动能定理有,解得 。)
小球从圆弧轨道上点飞出后做斜抛运动到点,竖直方向有 ,水平
方向有 ,解得 。
. .
考点4 动能定理求解多过程问题
8.(2023湖北卷)如图为某游戏装置原理示意图。水平
桌面上固定一半圆形竖直挡板,其半径为 、内表面
光滑,挡板的两端、在桌面边缘,与半径为 的固
定光滑圆弧轨道在同一竖直平面内,过 点的轨道
半径与竖直方向的夹角为 。小物块以某一水平初速
度由点切入挡板内侧,从点飞出桌面后,在 点沿圆
弧切线方向进入轨道 内侧,并恰好能到达轨道的最
高点。小物块与桌面之间的动摩擦因数为,重力加速度大小为 ,忽略空气阻力,
小物块可视为质点。求:
(1) 小物块到达 点的速度大小;
【答案】
【解析】 由题意可知,小物块恰好能到达轨道的最高点,则在点有
解得 。
(2) 和 两点的高度差;
【答案】 0
【解析】 由题意可知,小物块从点沿圆弧切线方向进入轨道内侧,则在 点有
小物块从点到 点的过程,根据动能定理有
小物块从点到 点的过程,根据动能定理有
联立解得, 。
(3) 小物块在 点的初速度大小。
【答案】
【解析】 小物块从点到 点的过程,根据动能定理有
解得 。
9.(2025福建福州一中开学考)如图所示,一轨道竖直放置,段和 段的倾角
均为 ,与水平段平滑连接,段的竖直圆形轨道半径为 ,其最低点处稍
微错开,使得滑块能进入或离开。段和 段粗糙,其余各段轨道均光滑。将一质量
为的滑块从轨道上离点距离处由静止释放,滑块经过圆形轨道后冲上 段
上升一段距离后再次滑下,往返滑动多次后静止于轨道上某处。滑块和轨道、 间
的动摩擦因数均为,重力加速度大小为,, 。求:
(1) 滑块第一次到达圆轨道最高点时对轨道的压力大小;
【答案】 45
【解析】 滑块从静止释放到第一次到达圆轨道最高点的过程,由动能定理有
在最高点,对滑块由牛顿第二定律有
解得
由牛顿第三定律可知,滑块第一次到达圆轨道最高点时对轨道的压力大小为
(2) 滑块第一次在 段向上滑行的最大距离;
【答案】
【解析】 滑块从静止释放到第一次在 段向上滑行到最高点的过程,设滑行的最大距
离为,由动能定理有
解得滑块第一次在段向上滑行的最大距离为
(3) 整个过程中滑块在 段滑行的总路程。
【答案】
【解析】 滑块开始第一次在 段下滑至第二次到达圆轨道最高点的过程,由动能定理
有
解得
设滑块第一次在段向上滑行的最大距离为 ,由动能定理有
解得
假设滑块第二次在 段向下滑行后可以第三次到达圆轨道最高点,由动能定理有
(【易错】需要判断能不能第三次通
过圆轨道最高点。)
解得 ,不符合实际
所以滑块第三次进入圆轨道无法到达最高点,假设其运动的过程中不脱轨且上升的最大
高度为
由动能定理可得,解得
所以滑块第三次进入圆轨道运动过程中没有脱轨,之后仅在 段与圆轨道间来回滑动,
最终停在 点
设之后滑块在段滑行的路程为,由动能定理有
整个过程中滑块在段滑行的总路程为
联立解得 。
. .
跳跳学长有话说
应用动能定理解题的一般步骤
10.(2024黑龙江大庆实验中学开学考试)极限运动深受年轻人的喜爱,图甲是极限运
动中滑板、轮滑等运动常用的比赛场地形池。现有某 形池场地示意图如图乙所示,
该场地由两段可视为光滑的圆弧形滑道和以及粗糙程度相同的水平滑道 构成,
图中,,。某次滑板比赛中质量为 (含滑板质量)
的运动员从点由静止出发,通过、滑道,冲向滑道,到达 滑道的最高位置
时速度恰好为零(运动员和滑板整体近似看成质点,空气阻力不计,重力加速度大小
取 )。
(1) 求该运动员在圆弧形滑道上下滑至 点时对圆弧形滑道的压力;
【答案】 ,方向垂直于 向下
【解析】 运动员从到 的过程中,由动能定理得
在 点由牛顿第二定律得
联立解得
由牛顿第三定律得,运动员对滑道 点的压力大小
,方向垂直于 向下。
(2) 该运动员为了第一次经过处后有时间做空中表演,求他在 点下滑的初速度大小;
【答案】
【解析】 设运动员在段克服摩擦力做的功为,根据运动员从点由静止出发到
点时的速度恰好为零,由动能定理得
解得
运动员离开点后在空中表演时做竖直上抛运动,上抛时的初速度
解得 。
运动员从到 过程,由动能定理得
代入数据解得
(3) 在(2)问的初始条件下,运动员在滑道上来回运动,最终停的位置距离 点多远?
【答案】
【解析】 运动员下落后会在滑道上来回运动,直到最终静止在 上,
运动的全过程由动能定理得
由,得
解得运动员在段的总路程为
在上来回运动的次数
即停在中间,所以运动员最终停在离点 处。
专题六 功和能
考向二 动能定理及其应用
2025年高考物理专题复习资料
考点切片
考点1 对动能定理的理解
解题觉醒
1.题型特征:应用动能定理求解相关物理量。
2.解题技巧
(1)多过程问题,优先对全程列动能定理方程;
(2)求时间,首选牛顿第二定律
3.解题步骤
(1)找出做功的力;
(2)计算动能变化量;
(3)
1.(2025贵州六校联盟模拟)巴黎奥运会网球女单决赛中,中国选手郑钦文以 战胜
克罗地亚选手维基奇夺冠。这是中国运动员史上首次赢得奥运网球单打项目的金牌。某
次运动员将质量为的网球击出,网球被击出瞬间距离地面的高度为 ,网球的速度大
小为,经过一段时间网球落地,落地瞬间的速度大小为 ,假设网球被击前瞬间,速
度大小为0,重力加速度大小为,网球克服空气阻力做的功为 。则下列说法正确的
是( )
D
A.击球过程,球拍对网球做的功为
B.网球从被击出到落地的过程,网球动能的增加量为
C.网球从被击出到落地的过程,网球的机械能减少
D.
【解析】 击球过程,根据动能定理有,即球拍对网球做的功为 。
网球从被击出到落地,根据动能定理有 。
根据功能关系可知,网球从被击出到落地,网球的机械能减少 。
根据动能定理有,解得 。
2.[多选](2023湖南卷)如图,固定在竖直面内的光滑轨道由直线段 和圆弧段
组成,两段相切于点,段与水平面夹角为 ,段圆心为,最高点为,与 的高
度差等于圆弧轨道的直径。小球从点以初速度 冲上轨道,能沿轨道运动恰好到达
点,下列说法正确的是(重力加速度大小为 )( )
AD
A.小球从到 的过程中,对轨道的压力逐渐增大
B.小球从到 的过程中,重力的功率始终保持不变
C.小球的初速度
D.若小球初速度增大,小球有可能从 点脱离轨道
【解析】 小球恰好运动至点,即小球在点速度 。
小球在圆弧上运动到 点的受力分析如图所示
小球从到 。
若小球在点的速度满足,则小球将从 点脱离轨道。
3.(2023重庆卷)机械臂广泛应用于机械装配。若某质量为 的
工件(视为质点)被机械臂抓取后,在竖直平面内由静止开始
斜向上做加速度大小为 的匀加速直线运动,运动方向与竖直方
向夹角为 ,提升高度为 ,如图所示。求:
(1) 提升高度为 时,工件的速度大小;
【答案】
【解析】 根据匀变速直线运动位移与速度关系有
解得 。
(2) 在此过程中,工件运动的时间及合力对工件做的功。
【答案】 ;
【解析】 根据速度—时间公式有
解得
根据动能定理有
解得 。
考点2 动能定理求解变力做功问题
4.(2025广东肇庆阶段练习)如图所示,某次特技表演中,一摩托车手沿平直路面向右
行驶,关闭发动机后,摩托车从路面末端点以大小 的速度水平飞出,恰好
从固定在竖直面内的粗糙圆弧轨道上(圆心为)的 点沿切线进入圆弧轨道,并恰好
能沿圆弧轨道通过最高点。已知圆弧轨道的半径,、 两点的连线与竖直
方向的夹角 。人与摩托车整体(视为质点)的质量 ,取重力加速度
大小,, ,不计空气阻力。求:
(1) 、两点间的水平距离 ;
【答案】 30
【解析】 设整体通过点时的速度大小为,有
整体通过点时的竖直分速度大小
设整体从点运动到点的时间为,有
又
解得 。
(2) 整体从点运动到点的过程中,克服轨道阻力做的功 。
【答案】
【解析】 由(1)可得,设整体通过点时的速度大小为,有
对整体从点运动到 点的过程,由动能定理可得
解得 。
5.(2024上海市七宝中学月考)如图所示,水平圆盘边缘有一个物块
(可看作质点),现将圆盘由静止开始绕过圆心的竖直轴转动,缓慢
增大圆盘的角速度,当圆盘转动的角速度增大到某一数值时,物块恰
从圆盘边缘滑落。已知圆盘半径为,物块的质量为 ,物块与圆盘
间的动摩擦因数为 ,最大静摩擦力等于滑动摩擦力,水平圆盘与地
面的高度差为,重力加速度大小为 。求:
(1) 物块恰好滑离圆盘边缘的线速度 的大小;
【答案】
【解析】 物块恰好滑离圆盘时摩擦力达到最大静摩擦力,
由牛顿第二定律有
解得 。
(2) 圆盘从静止开始至物块滑离圆盘的过程,摩擦力对物块所做的功 ;
【答案】
【解析】 圆盘从静止开始至物块滑离圆盘过程中,
由动能定理有
可得 。
(3) 物块落地点到圆盘中心的水平距离 。
【答案】
【解析】 物块将沿着圆盘切线方向滑离圆盘做平抛运动,设物块落地时间为 ,做平抛
运动的水平位移为,则有,
解得
则可得物块落地点到圆盘中心的水平距离 。(【易错】容
易将平抛运动的水平位移 当成物块落地点到圆盘中心的水平距离。)
. .
考点3 动能定理求解竖直圆问题
解题觉醒
1.题型特征:小球在竖直圆中运动。
2.解题技巧:口诀“力径减半得动能”。公式 。
如图,小球质量为,做圆周运动的半径为,小球从到 过程摩
擦力做的功为 。
小球在点的动能为,小球在点的动能为 ,
根据动能定理得 。
6.(2024四川遂宁模拟)如图所示,一小球以一定的初速度从图示位置进入光滑的轨道,
小球先进入圆轨道1,再进入圆轨道2,圆轨道1的半径为 ,圆轨道2的半径是轨道1的
1.8倍,小球的质量为。若小球恰好能通过轨道2的最高点 ,则小球在轨道1上经过其
最高点时对轨道的压力大小为(重力加速度大小为 )( )
C
A. B. C. D.
【解析】 小球恰好能通过轨道2的最高点 ,运用大招口诀“力径减半得动能”(【提醒】
注意运用大招“力径减半得动能”公式时,若是选择题、填空题可直接写出,若是计算题
需要写出解答过程的,必须写出规范的动能定理公式,为了简化运算我们可以在草稿纸
上列大招公式进行代替。)得,小球从到 的过程,由动
能定理得,其中为小球在点的向心力,在 点由
牛顿第二定律得,解得 ,由牛顿第三定律可知小球在轨道1上经
过其最高点时对轨道的压力大小为 。
7.[多选](2024黑龙江双鸭山市一中模拟)如图所示,
在光滑的斜轨道底端平滑连接着一个半径为 、顶端有缺
口的光滑圆弧轨道,点、点在同一水平面上, 点是最
低点, 。一质量为 的小球由斜轨道上某高
度处静止释放,由轨道连接处进入圆弧轨道。重力加速度
BD
A.若小球滑到点时速度大小为,则此处轨道对小球作用力的大小为
B.若小球滑到点时速度大小为,则小球滑到点时速度大小为
C.若小球恰好能通过圆弧形轨道上点,则小球在斜轨道上静止释放的高度为
D.若小球从圆弧形轨道上点飞出后恰好从点飞入圆弧形轨道,则小球经过 点时的速
度大小为
大小为 ,不考虑机械能的损失,下列说法正确的是 ( )
【解析】 小球在点,根据牛顿第二定律有 ,则此处轨道对小球作
用力的大小为 。
小球从圆弧轨道最低点滑到 点,由动能定理有
,解得 。
若小球恰好能通过圆弧轨道内点,根据牛顿第二定律有 ,小球
从释放到点,根据动能定理有,解得 。
(【大招运用】根据大招内容中口诀“力径减半得动能”可知小球到达 点时的动能为
,由动能定理有,解得 。)
小球从圆弧轨道上点飞出后做斜抛运动到点,竖直方向有 ,水平
方向有 ,解得 。
. .
考点4 动能定理求解多过程问题
8.(2023湖北卷)如图为某游戏装置原理示意图。水平
桌面上固定一半圆形竖直挡板,其半径为 、内表面
光滑,挡板的两端、在桌面边缘,与半径为 的固
定光滑圆弧轨道在同一竖直平面内,过 点的轨道
半径与竖直方向的夹角为 。小物块以某一水平初速
度由点切入挡板内侧,从点飞出桌面后,在 点沿圆
弧切线方向进入轨道 内侧,并恰好能到达轨道的最
高点。小物块与桌面之间的动摩擦因数为,重力加速度大小为 ,忽略空气阻力,
小物块可视为质点。求:
(1) 小物块到达 点的速度大小;
【答案】
【解析】 由题意可知,小物块恰好能到达轨道的最高点,则在点有
解得 。
(2) 和 两点的高度差;
【答案】 0
【解析】 由题意可知,小物块从点沿圆弧切线方向进入轨道内侧,则在 点有
小物块从点到 点的过程,根据动能定理有
小物块从点到 点的过程,根据动能定理有
联立解得, 。
(3) 小物块在 点的初速度大小。
【答案】
【解析】 小物块从点到 点的过程,根据动能定理有
解得 。
9.(2025福建福州一中开学考)如图所示,一轨道竖直放置,段和 段的倾角
均为 ,与水平段平滑连接,段的竖直圆形轨道半径为 ,其最低点处稍
微错开,使得滑块能进入或离开。段和 段粗糙,其余各段轨道均光滑。将一质量
为的滑块从轨道上离点距离处由静止释放,滑块经过圆形轨道后冲上 段
上升一段距离后再次滑下,往返滑动多次后静止于轨道上某处。滑块和轨道、 间
的动摩擦因数均为,重力加速度大小为,, 。求:
(1) 滑块第一次到达圆轨道最高点时对轨道的压力大小;
【答案】 45
【解析】 滑块从静止释放到第一次到达圆轨道最高点的过程,由动能定理有
在最高点,对滑块由牛顿第二定律有
解得
由牛顿第三定律可知,滑块第一次到达圆轨道最高点时对轨道的压力大小为
(2) 滑块第一次在 段向上滑行的最大距离;
【答案】
【解析】 滑块从静止释放到第一次在 段向上滑行到最高点的过程,设滑行的最大距
离为,由动能定理有
解得滑块第一次在段向上滑行的最大距离为
(3) 整个过程中滑块在 段滑行的总路程。
【答案】
【解析】 滑块开始第一次在 段下滑至第二次到达圆轨道最高点的过程,由动能定理
有
解得
设滑块第一次在段向上滑行的最大距离为 ,由动能定理有
解得
假设滑块第二次在 段向下滑行后可以第三次到达圆轨道最高点,由动能定理有
(【易错】需要判断能不能第三次通
过圆轨道最高点。)
解得 ,不符合实际
所以滑块第三次进入圆轨道无法到达最高点,假设其运动的过程中不脱轨且上升的最大
高度为
由动能定理可得,解得
所以滑块第三次进入圆轨道运动过程中没有脱轨,之后仅在 段与圆轨道间来回滑动,
最终停在 点
设之后滑块在段滑行的路程为,由动能定理有
整个过程中滑块在段滑行的总路程为
联立解得 。
. .
跳跳学长有话说
应用动能定理解题的一般步骤
10.(2024黑龙江大庆实验中学开学考试)极限运动深受年轻人的喜爱,图甲是极限运
动中滑板、轮滑等运动常用的比赛场地形池。现有某 形池场地示意图如图乙所示,
该场地由两段可视为光滑的圆弧形滑道和以及粗糙程度相同的水平滑道 构成,
图中,,。某次滑板比赛中质量为 (含滑板质量)
的运动员从点由静止出发,通过、滑道,冲向滑道,到达 滑道的最高位置
时速度恰好为零(运动员和滑板整体近似看成质点,空气阻力不计,重力加速度大小
取 )。
(1) 求该运动员在圆弧形滑道上下滑至 点时对圆弧形滑道的压力;
【答案】 ,方向垂直于 向下
【解析】 运动员从到 的过程中,由动能定理得
在 点由牛顿第二定律得
联立解得
由牛顿第三定律得,运动员对滑道 点的压力大小
,方向垂直于 向下。
(2) 该运动员为了第一次经过处后有时间做空中表演,求他在 点下滑的初速度大小;
【答案】
【解析】 设运动员在段克服摩擦力做的功为,根据运动员从点由静止出发到
点时的速度恰好为零,由动能定理得
解得
运动员离开点后在空中表演时做竖直上抛运动,上抛时的初速度
解得 。
运动员从到 过程,由动能定理得
代入数据解得
(3) 在(2)问的初始条件下,运动员在滑道上来回运动,最终停的位置距离 点多远?
【答案】
【解析】 运动员下落后会在滑道上来回运动,直到最终静止在 上,
运动的全过程由动能定理得
由,得
解得运动员在段的总路程为
在上来回运动的次数
即停在中间,所以运动员最终停在离点 处。
同课章节目录
