考向三 机械能守恒定律及其应用-2025年高考物理专题复习课件
文档属性
| 名称 | 考向三 机械能守恒定律及其应用-2025年高考物理专题复习课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-02-18 09:45:54 | ||
图片预览





文档简介
(共18张PPT)
专题六 功和能
考向三 机械能守恒定律及其应用
2025年高考物理专题复习资料
考点切片
考点1 单物体机械能守恒
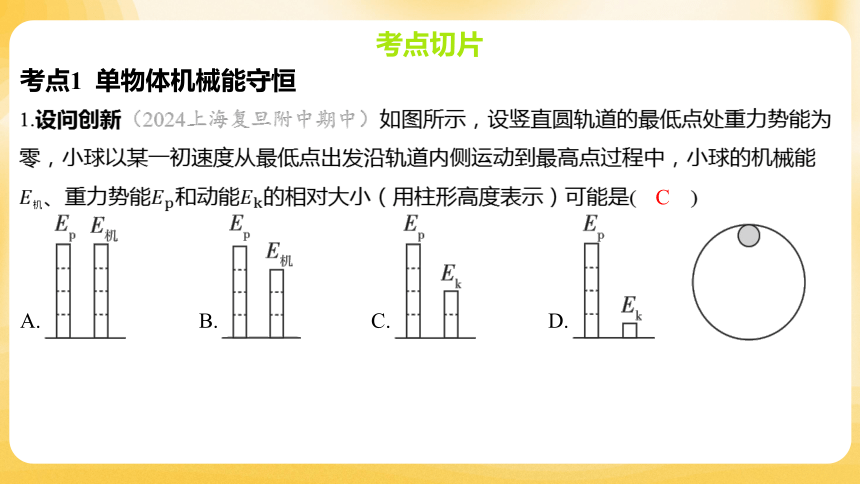
1.设问创新(2024上海复旦附中期中)如图所示,设竖直圆轨道的最低点处重力势能为
零,小球以某一初速度从最低点出发沿轨道内侧运动到最高点过程中,小球的机械能
、重力势能和动能 的相对大小(用柱形高度表示)可能是( )
C
A. B. C. D.
【解析】 若小球恰能到达最高点,则 ,此时小球在最高点的动能
,重力势能 ,小球运动过程中机械能守恒,因
,小球的动能不可能为零,则小球的机械能不可能等于重力势能,重力势
能不可能大于机械能,小球的动能最少是重力势能的四分之一,则小球的重力势能可能
等于动能的2倍。
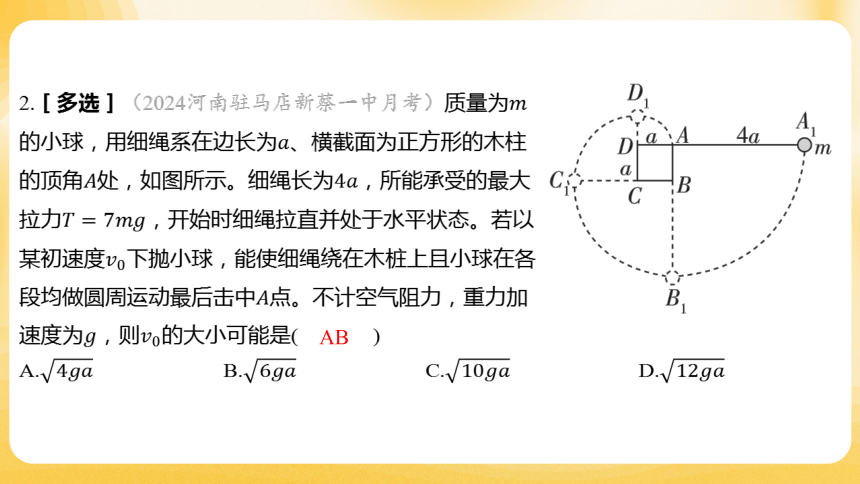
2.[多选](2024河南驻马店新蔡一中月考)质量为
的小球,用细绳系在边长为 、横截面为正方形的木柱
的顶角处,如图所示。细绳长为 ,所能承受的最大
拉力 ,开始时细绳拉直并处于水平状态。若以
某初速度 下抛小球,能使细绳绕在木桩上且小球在各
段均做圆周运动最后击中 点。不计空气阻力,重力加
速度为,则 的大小可能是( )
AB
A. B. C. D.
【解析】 小球在各段均做圆周运动,分析可知速度取最小值时,小球恰好能
到达 点,而最大速度则取决于细绳所能承受的最大拉力,需要分别计算出小球在
、、三点时的最大速度,得的取值范围为 。
位置 分析 最小(最大)速度
点 以点为圆心运动到最高点,有,从 到 根据机械能守恒定律有
点 运动到点,有,从到 ,根据机 械能守恒定律有
点 运动到点有,从到 根据机械能守恒定 律有
A点 运动到点,有,从到 根据机械能守恒定 律有
考点2 多物体机械能守恒
3.(2024吉林长春期末)如图所示,在固定的光滑水平杆上,质量为的物体 用细线
跨过光滑的定滑轮连接质量为的物体,用手托住 使整个系统静止,此时细线刚好
拉直,且,,,重力加速度大小为。释放 ,让二者开始运动,
则下列说法正确的是( )
C
A.始终比 运动得快
B.在物体从滑到的过程中,的机械能减小, 的机械能增
加
C.运动的最大速度为
D.开始运动后,当的速度再次为零时,下降了
【解析】 设与水平方向的夹角为 ,根据速度关联可得 。
当物体滑到点时, 下降到最低点,速度为零,所以在该过程中,根据系统机
械能守恒可知,的机械能减小, 的机械能增大。
当运动到处时,的速度最大,(【点拨】运动到 处后继续向右运动,由于细
线做负功,做减速运动至速度为零。)根据系统机械能守恒可得 ,
解得运动的最大速度为 。
开始运动后,当的速度再次为零时,即的机械能不变,则 的机械能也不变,
说明此时 回到初始释放的位置。
. .
4.[多选](2024山西吕梁模拟)如图所示,光滑杆1、2
分别水平、竖直固定放置,交点为,质量 的
甲物块套在杆2上,质量 的乙物块套在杆1上,甲、
乙(均视为质点)用长度 的轻杆3铰接,当杆3与1
的夹角为 时,甲由静止开始释放,重力加速度大小取
,, ,下列说法正
确的是( )
BC
A.当杆3与杆2的夹角为 时,甲与的距离为
B.甲从静止释放到杆3与杆2的夹角为 时,系统重力势能的减小量为
C.当杆3与杆2的夹角为 时,乙的速度大小为
D.甲从静止释放到杆3与杆2的夹角为 时,杆3对乙做的功为
【解析】 当杆3与杆2的夹角为 时,甲与的距离 。
杆3与杆1的夹角为 时,甲与的距离 ,则系统的重力势能的
减小量,解得 。
当杆3与杆2的夹角为 时,设甲、乙的速度分别
为、 ,对此时甲、乙速度分别沿杆3方向和垂直杆3
方向分解,如图所示。则有 ,
(【点拨】甲、乙沿杆方向速度大小相等。)由系统的
由动能定理可得杆3对乙做的功为,解得 。
机械能守恒定律可得,解得 。
. .
跳跳学长有话说
对于多个物体组成的系统,在判断系统机械能是否守恒时,一定要检查过程中外力做的
总功是否为零,如本题若杆1、2为粗糙杆则过程中便会有能量损失,整个系统的机械能
不守恒。
考点3 非质点类物体机械能守恒
5.如图所示,质量分布均匀的铁链,静止放在半径 的光滑半圆管中。给铁链一
个微小的扰动使之向右沿管内壁下滑,当铁链的端点滑至 处时铁链速度大小为
。已知 ,以 所在水平面为参考平面,重力加速度大小取
,则下列说法中正确的是( )
C
A.铁链下滑过程中靠近 端的一小段铁链机械能守恒
B.铁链在初始位置时重心高度为
C.铁链的端点滑至处时铁链的重心下降
D.铁链的端点滑至处时铁链的速度大小为
【解析】 铁链下滑过程中靠近 端的一小段铁链受到上边铁链的拉力,该拉力做
负功,所以这一小段铁链的机械能不守恒。
根据几何关系可知,铁链长度为 ,铁链全部在半球体上时,铁链质量
分布均匀且形状规则,则其重心在几何中心,即铁链重心在 的平分线上,
(【易错】铁链重心不在连线上,也不在、 之间的铁链上)故铁链在初始位置时
铁链。
. .
. .
重心与球心连线长度等于端点滑至处时铁链重心与球心连线长度,均设为 ,对
铁链从开始到端点滑至处,根据机械能守恒定律有 ,
代入数据解得 。
铁链的端点滑至处时,铁链重心在处正下方处,则铁链的端点滑至 点时铁
链重心下降 。
铁链的端点滑至处的过程,对铁链根据机械能守恒定律有 ,解得
。
6.(2024江西吉安期末)如图所示,有一条长为的均匀金属链条,有 在光
滑的足够高的斜面上,另竖直下垂在空中,在外力作用下静止不动。斜面顶端 是一
个很小的光滑圆弧,斜面倾角为 。忽略空气阻力,重力加速度大小取 ,
。当撤去外力后链条滑动,则链条刚好全部越过 时的速率为( )
B
A. B. C. D.
【解析】 第一步:判断链条沿斜面下滑还是竖直下滑
设链条的质量为,斜面部分链条的质量为 ,该部分链条的重力沿斜面方向分力为
,竖直下垂部分链条的质量为,其重力为 ,由
,可知链条沿着斜面下滑。
第二步:找出变化前后链条的机械能
链条沿斜面下滑的过程只有重力做功,机械能守恒,以 点所在水平面为零势能面,变
化前左边链条的机械能为,右边链条的机械能为 ;变
化后链条的重力势能为 ,设此时动能为 。
第三步:根据机械能守恒列方程求解
,解得链条刚好全部越
过时的速率 ,故选B。
跳跳学长有话说
对于绳索、链条之类,在运动过程中物体常发生形变,正确确定其重心的位置是解决该
问题的关键。
专题六 功和能
考向三 机械能守恒定律及其应用
2025年高考物理专题复习资料
考点切片
考点1 单物体机械能守恒
1.设问创新(2024上海复旦附中期中)如图所示,设竖直圆轨道的最低点处重力势能为
零,小球以某一初速度从最低点出发沿轨道内侧运动到最高点过程中,小球的机械能
、重力势能和动能 的相对大小(用柱形高度表示)可能是( )
C
A. B. C. D.
【解析】 若小球恰能到达最高点,则 ,此时小球在最高点的动能
,重力势能 ,小球运动过程中机械能守恒,因
,小球的动能不可能为零,则小球的机械能不可能等于重力势能,重力势
能不可能大于机械能,小球的动能最少是重力势能的四分之一,则小球的重力势能可能
等于动能的2倍。
2.[多选](2024河南驻马店新蔡一中月考)质量为
的小球,用细绳系在边长为 、横截面为正方形的木柱
的顶角处,如图所示。细绳长为 ,所能承受的最大
拉力 ,开始时细绳拉直并处于水平状态。若以
某初速度 下抛小球,能使细绳绕在木桩上且小球在各
段均做圆周运动最后击中 点。不计空气阻力,重力加
速度为,则 的大小可能是( )
AB
A. B. C. D.
【解析】 小球在各段均做圆周运动,分析可知速度取最小值时,小球恰好能
到达 点,而最大速度则取决于细绳所能承受的最大拉力,需要分别计算出小球在
、、三点时的最大速度,得的取值范围为 。
位置 分析 最小(最大)速度
点 以点为圆心运动到最高点,有,从 到 根据机械能守恒定律有
点 运动到点,有,从到 ,根据机 械能守恒定律有
点 运动到点有,从到 根据机械能守恒定 律有
A点 运动到点,有,从到 根据机械能守恒定 律有
考点2 多物体机械能守恒
3.(2024吉林长春期末)如图所示,在固定的光滑水平杆上,质量为的物体 用细线
跨过光滑的定滑轮连接质量为的物体,用手托住 使整个系统静止,此时细线刚好
拉直,且,,,重力加速度大小为。释放 ,让二者开始运动,
则下列说法正确的是( )
C
A.始终比 运动得快
B.在物体从滑到的过程中,的机械能减小, 的机械能增
加
C.运动的最大速度为
D.开始运动后,当的速度再次为零时,下降了
【解析】 设与水平方向的夹角为 ,根据速度关联可得 。
当物体滑到点时, 下降到最低点,速度为零,所以在该过程中,根据系统机
械能守恒可知,的机械能减小, 的机械能增大。
当运动到处时,的速度最大,(【点拨】运动到 处后继续向右运动,由于细
线做负功,做减速运动至速度为零。)根据系统机械能守恒可得 ,
解得运动的最大速度为 。
开始运动后,当的速度再次为零时,即的机械能不变,则 的机械能也不变,
说明此时 回到初始释放的位置。
. .
4.[多选](2024山西吕梁模拟)如图所示,光滑杆1、2
分别水平、竖直固定放置,交点为,质量 的
甲物块套在杆2上,质量 的乙物块套在杆1上,甲、
乙(均视为质点)用长度 的轻杆3铰接,当杆3与1
的夹角为 时,甲由静止开始释放,重力加速度大小取
,, ,下列说法正
确的是( )
BC
A.当杆3与杆2的夹角为 时,甲与的距离为
B.甲从静止释放到杆3与杆2的夹角为 时,系统重力势能的减小量为
C.当杆3与杆2的夹角为 时,乙的速度大小为
D.甲从静止释放到杆3与杆2的夹角为 时,杆3对乙做的功为
【解析】 当杆3与杆2的夹角为 时,甲与的距离 。
杆3与杆1的夹角为 时,甲与的距离 ,则系统的重力势能的
减小量,解得 。
当杆3与杆2的夹角为 时,设甲、乙的速度分别
为、 ,对此时甲、乙速度分别沿杆3方向和垂直杆3
方向分解,如图所示。则有 ,
(【点拨】甲、乙沿杆方向速度大小相等。)由系统的
由动能定理可得杆3对乙做的功为,解得 。
机械能守恒定律可得,解得 。
. .
跳跳学长有话说
对于多个物体组成的系统,在判断系统机械能是否守恒时,一定要检查过程中外力做的
总功是否为零,如本题若杆1、2为粗糙杆则过程中便会有能量损失,整个系统的机械能
不守恒。
考点3 非质点类物体机械能守恒
5.如图所示,质量分布均匀的铁链,静止放在半径 的光滑半圆管中。给铁链一
个微小的扰动使之向右沿管内壁下滑,当铁链的端点滑至 处时铁链速度大小为
。已知 ,以 所在水平面为参考平面,重力加速度大小取
,则下列说法中正确的是( )
C
A.铁链下滑过程中靠近 端的一小段铁链机械能守恒
B.铁链在初始位置时重心高度为
C.铁链的端点滑至处时铁链的重心下降
D.铁链的端点滑至处时铁链的速度大小为
【解析】 铁链下滑过程中靠近 端的一小段铁链受到上边铁链的拉力,该拉力做
负功,所以这一小段铁链的机械能不守恒。
根据几何关系可知,铁链长度为 ,铁链全部在半球体上时,铁链质量
分布均匀且形状规则,则其重心在几何中心,即铁链重心在 的平分线上,
(【易错】铁链重心不在连线上,也不在、 之间的铁链上)故铁链在初始位置时
铁链。
. .
. .
重心与球心连线长度等于端点滑至处时铁链重心与球心连线长度,均设为 ,对
铁链从开始到端点滑至处,根据机械能守恒定律有 ,
代入数据解得 。
铁链的端点滑至处时,铁链重心在处正下方处,则铁链的端点滑至 点时铁
链重心下降 。
铁链的端点滑至处的过程,对铁链根据机械能守恒定律有 ,解得
。
6.(2024江西吉安期末)如图所示,有一条长为的均匀金属链条,有 在光
滑的足够高的斜面上,另竖直下垂在空中,在外力作用下静止不动。斜面顶端 是一
个很小的光滑圆弧,斜面倾角为 。忽略空气阻力,重力加速度大小取 ,
。当撤去外力后链条滑动,则链条刚好全部越过 时的速率为( )
B
A. B. C. D.
【解析】 第一步:判断链条沿斜面下滑还是竖直下滑
设链条的质量为,斜面部分链条的质量为 ,该部分链条的重力沿斜面方向分力为
,竖直下垂部分链条的质量为,其重力为 ,由
,可知链条沿着斜面下滑。
第二步:找出变化前后链条的机械能
链条沿斜面下滑的过程只有重力做功,机械能守恒,以 点所在水平面为零势能面,变
化前左边链条的机械能为,右边链条的机械能为 ;变
化后链条的重力势能为 ,设此时动能为 。
第三步:根据机械能守恒列方程求解
,解得链条刚好全部越
过时的速率 ,故选B。
跳跳学长有话说
对于绳索、链条之类,在运动过程中物体常发生形变,正确确定其重心的位置是解决该
问题的关键。
同课章节目录
