考向一 电场力的性质-2025年高考物理专题复习课件
文档属性
| 名称 | 考向一 电场力的性质-2025年高考物理专题复习课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-02-18 00:00:00 | ||
图片预览




文档简介
(共29张PPT)
专题八 静电场
考向一 电场力的性质
2025年高考物理专题复习资料
考点切片
考点1 电荷守恒定律和库仑定律
1.(2024山东济南期末)三个完全相同的带电导体球、、,带电荷量分别为 、
0和,让与先接触,然后让与接触,最终 所带的电荷量为( )
A
A. B. C. D.
【解析】 三个带电导体球完全相同,根据电荷守恒定律得,与 先接触后两球带
电荷量均为,再让与 接触,两球最终带电荷量均为
(【点拨】完全相同的导体球接触后带电荷量先中和再平分。)。
. .
. .
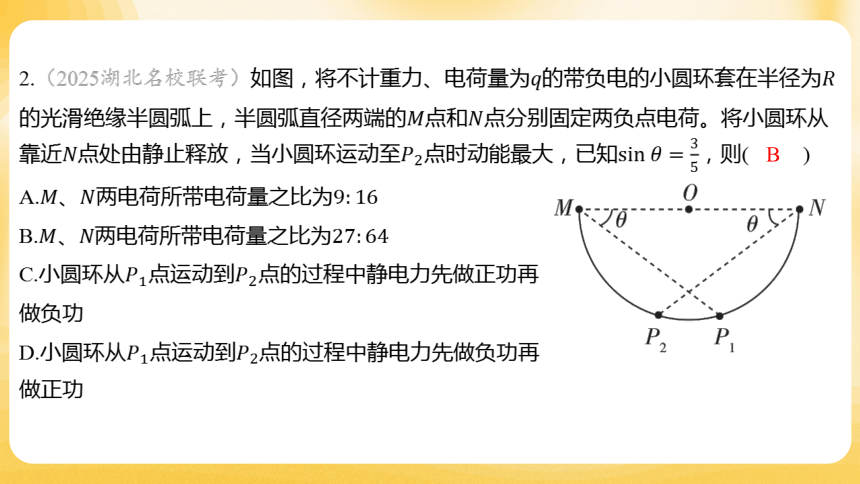
2.(2025湖北名校联考)如图,将不计重力、电荷量为的带负电的小圆环套在半径为
的光滑绝缘半圆弧上,半圆弧直径两端的点和 点分别固定两负点电荷。将小圆环从
靠近点处由静止释放,当小圆环运动至点时动能最大,已知 ,则( )
B
A.、两电荷所带电荷量之比为
B.、两电荷所带电荷量之比为
C.小圆环从点运动到 点的过程中静电力先做正功再
做负功
D.小圆环从点运动到 点的过程中静电力先做负功再
做正功
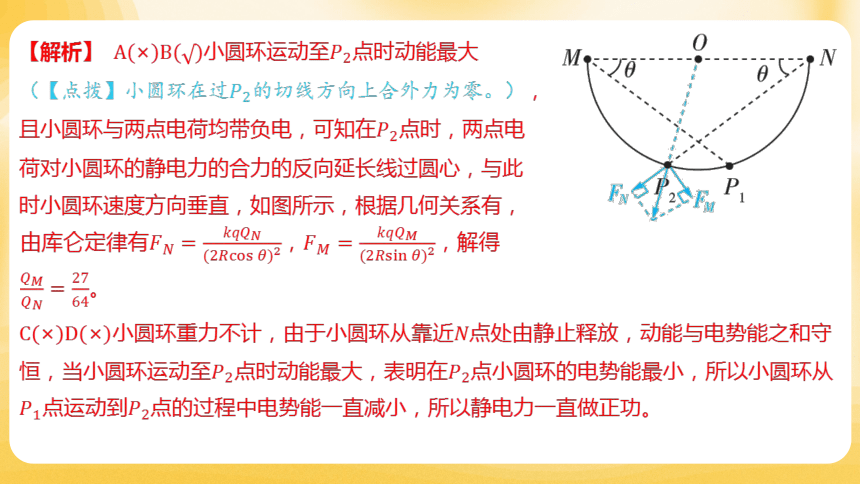
【解析】 小圆环运动至 点时动能最大
(【点拨】小圆环在过 的切线方向上合外力为零。),
且小圆环与两点电荷均带负电,可知在 点时,两点电
荷对小圆环的静电力的合力的反向延长线过圆心,与此
时小圆环速度方向垂直,如图所示,根据几何关系有,
小圆环重力不计,由于小圆环从靠近 点处由静止释放,动能与电势能之和守
恒,当小圆环运动至点时动能最大,表明在 点小圆环的电势能最小,所以小圆环从
点运动到 点的过程中电势能一直减小,所以静电力一直做正功。
由库仑定律有, ,解得
。
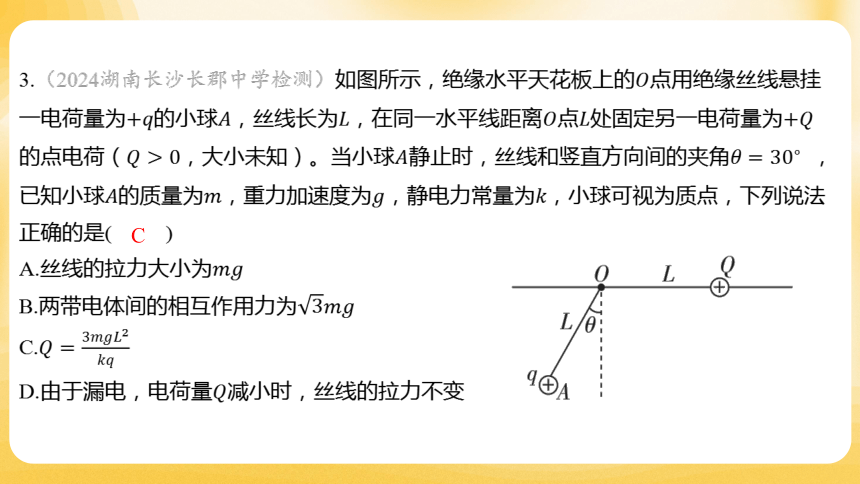
3.(2024湖南长沙长郡中学检测)如图所示,绝缘水平天花板上的 点用绝缘丝线悬挂
一电荷量为的小球,丝线长为,在同一水平线距离点处固定另一电荷量为
的点电荷(,大小未知)。当小球静止时,丝线和竖直方向间的夹角 ,
已知小球的质量为,重力加速度为,静电力常量为 ,小球可视为质点,下列说法
正确的是( )
C
A.丝线的拉力大小为
B.两带电体间的相互作用力为
C.
D.由于漏电,电荷量 减小时,丝线的拉力不变
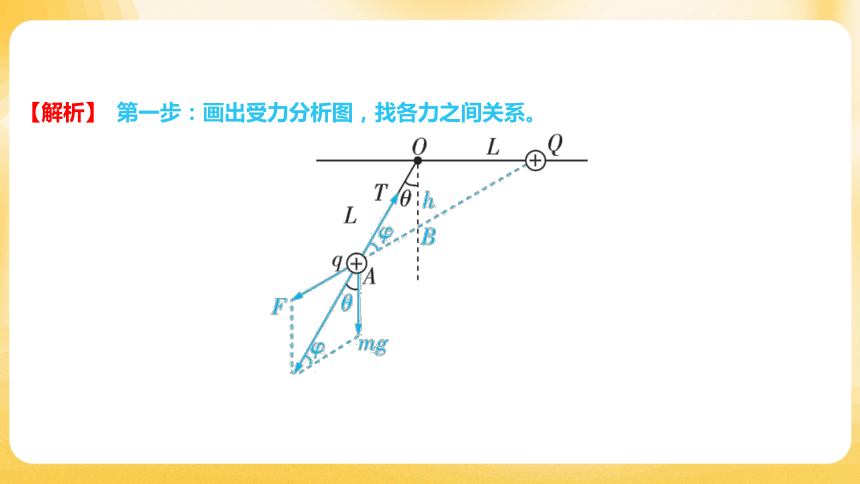
【解析】 第一步:画出受力分析图,找各力之间关系。
设小球和点电荷间的库仑力为,小球 受力情况如图所示,由几何关系可知
,再结合力的矢量运算可得两带电体间的相互作用力 ,丝线的拉力
。
根据库仑定律有,解得 。
第二步:找出相似三角形。
设过点的竖直线与、连线的交点为,、间距离为,由于漏电,电荷量 减
小时,小球将下移,故 变大,由力的分析图可知三力组成的矢量三角形和三角形
相似,根据相似三角形对应边比值相等可得,当 变大、丝线长度不变时,
丝线的拉力减小。
考点2 电场强度
题组1 电场的基本性质
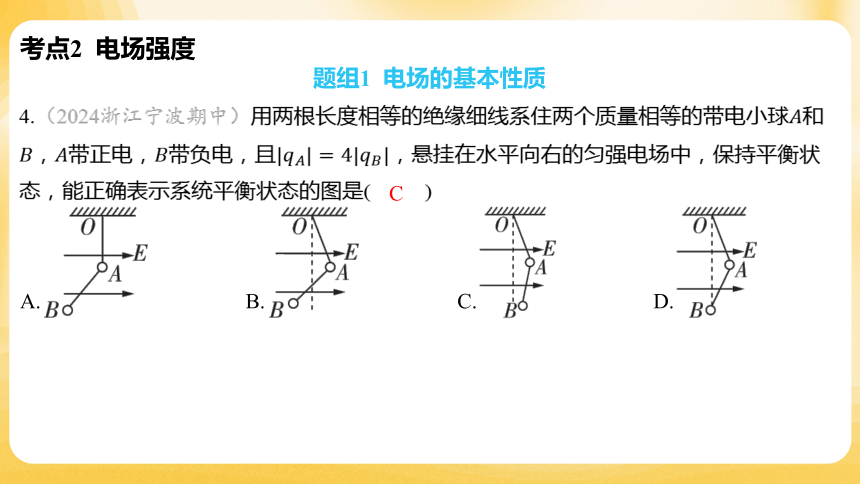
4.(2024浙江宁波期中)用两根长度相等的绝缘细线系住两个质量相等的带电小球 和
,带正电,带负电,且 ,悬挂在水平向右的匀强电场中,保持平衡状
态,能正确表示系统平衡状态的图是( )
C
A. B. C. D.
【解析】 设,带正电,受到的电场力水平向右, 带负电,受
到的电场力水平向左。以整体为研究对象,设、间的细线与竖直方向的夹角为 ,
则由平衡条件得;以小球为研究对象,受力如图所示,设、 间的细线
与竖直方向的夹角为 ,则由平衡条件得,可得 。
5.(2024吉林通化期末)如图所示,长为 、不可伸长的绝缘细线一端系一质量为
的可视为质点的带电小球,另一端悬挂在 点,当空中存在水平向右、大小
为的匀强电场时,小球偏转 后在点处于静止状态。 ,
,重力加速度取 。
(1) 分析小球的带电性质及带电荷量;
【答案】 正电;
【解析】 设小球的质量为,带电荷量为,电场强度大小为 ,细线
的拉力为 ,对小球进行受力分析,因小球静止,故受力情况如图所示,
因小球所受电场力方向与电场方向同向,故小球带正电。小球受力平衡,
则有
(2) 求细线的拉力大小;
【答案】
【解析】 根据受力分析图可知 。
解得 。
(3) 改变电场强度的大小和方向,为使小球仍保持静止在 点,求电场强度的最小值
和方向。
【答案】 ; 方向垂直于 斜向右上方
【解析】 重力、细线的拉力和电场力三力可构成闭合矢量三角形。重力的大小、方向
均不变,细线拉力方向不变,由几何关系可知,当电场力的方向与细线的拉力方向垂直
时,电场力取最小值,电场强度最小,设为 ,则
解得
方向垂直于 斜向右上方。
题组2 电场强度 电场强度的叠加
解题觉醒
1.题型特征
(1)三点法:匀强电场中,已知几何关系和三点电势,求电场强度的方向和大小。
(2)正交分解法:匀强电场中,已知几个点的电 势或电势差,题图有垂直关系,求电场强度。
(3)割补法:空间存在多个点电荷,图形对称,某位置电荷量不同,求电场强度。
2.解题步骤
(1)三点法:①找电势相等的点;②连等势线;③作等势线的垂线;④求电场强度。
(2)正交分解法:①找到两条垂直线段;②根据电势差、距离计算两个分电场强度;
③使用勾股定理计算合电场强度。
(3)割补法:通过割补,灵活构造对称,进而利用对称性和矢量叠加法,结合点电荷
场强公式求电场强度。
6.[多选](2024湖南永州月考)如图所示,在匀强
电场中建立直角坐标系,原点的电势为, 点坐
标为,电势为,点坐标为 ,
电势为 ,则该电场的电场强度
( )
BC
A.方向与轴正向成 向右上方
B.方向与轴负向成 向左下方
C.大小为
D.大小为
【解析】 运用大招46三点法求电场强度。如图所示。
第一步:找三点的最低点和最高点。
连接、两点,取的中点,可得点的电势为,与 点相同。
第二步:找等势线。
连接、两点,线段 即为等势线。
第三步:作等势线的垂线。
过点作等势线的垂线交于点,即为电场线,方向为由点指向 点,由几何
关系可知,与轴负方向的夹角为 。
第四步:求出电场强度大小。
由几何关系可知,、两点的电势差为 ,可求出匀强电场的电场强度
大小为 。故选B、C。
跳跳学长传妙招
已知三点电势求场强的方法
等分法 平行结论法 正交分解法
_____________________________________ ___________________________________ ___________________________________
匀强电场中同一条直线 上的线段两端点间电势 差正比于线段长度 匀强电场中,若两线段平行,则这 两线段各自的端点间电势差正比于 线段长度。题中出现平行线时可用 此方法 匀强电场中利用 ,
分别求出两垂直方向的场
强,再求出合场强
7.(2024湖南邵阳模拟)一圆心在点、半径的半圆,为其直径, 是半圆
上的一点, ,半圆所在的平面内有一匀强电场,、、 三点的电势分别
为、、。已知, ,则下列说法
正确的是( )
C
A.该匀强电场的电场强度的方向与直径的夹角为
B.该匀强电场的电场强度的方向与直径的夹角为
C.该匀强电场的电场强度大小为
D.该匀强电场的电场强度大小为
【解析】 题图中有垂直关系 ,运用正交分解法求电场强度。
第一步:如图所示,找到两条垂直线段和 。
, ,, 。
第二步:根据电势差、距离计算两个分电场强度。
, 。
第三步:使用勾股定理计算合电场强度。
, ,电场强度的方向沿半径 方向,
即电场强度方向与直径的夹角为 。
8.(2024河北卷)如图,真空中有两个电荷量均为
的点电荷,分别固定在正三角形的顶点 、
。为三角形的中心,沿 的中垂线对称放置一根
与三角形共面的均匀带电细杆,电荷量为 。已知正三角
形的边长为,点的电场强度为0,静电力常量为 。
顶点 处的电场强度大小为( )
D
A. B. C. D.
【解析】 第一步:由点电荷场强公式及场强的叠加计算、点的电荷在 点的场强
B、点的电荷在的场强的合场强为 。
第二步:计算带电细杆在 点的场强
点的合场强为零,因此带电细杆在点的场强大小 。
第三步:由对称性及场强叠加计算 点的场强
由对称性可知,带电细杆在点的场强大小为,方向竖直向上,因此 点处
的合场强为 ,D项正确。
9.(2024云南昆明一中模拟)均匀带电的球
壳在球外空间产生的电场等效于电荷集中于
球心处的点电荷产生的电场。如图所示,在
绝缘球球面 上均匀分布正电荷,总
C
A. B. C. D.
电荷量为;在剩余球面上均匀分布负电荷,总电荷量是。球半径为 ,球心为
,为球面的对称轴,在轴线上有、两点,且 ,
,。已知球面在点的场强大小为,静电力常量为 ,
则 点的场强大小为( )
【解析】 将 部分补上,使球壳变成一个均匀带正电的完整的球壳,完整球壳带电荷
量为,为保证电荷量不变,球面带负电荷量为,则该球壳带正电的部分在
点产生的场强为,根据对称性可知:①带正电的部分完整球壳在 点产
生的场强大小;②球面带负电荷量为,在点产生的场强大小为 ,两者
方向相反;则点的场强大小为 ,故选C。
10.(2024湖南名校联考)理论分析表明,一根长为 的均匀带正
电的细杆竖直放置,当时,细杆两端处的场强 ,
细杆中间处的场强。其中为常数, 为电荷线密度
(细杆带电荷量与长度的比值), 为点到细杆的垂直距离,如图
甲所示。若再取一根与完全一样的均匀带正电细杆 ,平行放置
在的右侧,距离为 ,如图乙所示。它们端点的连线上
A
A.1处合场强大小为 B.2处合场强方向竖直向下
C.3处合场强大小为 D.3、4处合场强方向不同
有点1、2、3、4,其中1、3到杆的距离均为,各点到两杆的距离均远小于杆长 。关
于各点场强的大小与方向,下列说法正确的是( )
【解析】
题干分析 将细杆中间断开看成两根细杆,则中间点的场强为 ,可 得 ,即细杆在两端的场强的方向与水平方向的夹角为 1处场强如图 _______________________ 1到、两杆的距离均为 则1处的合场强为 A(√)
2处场强如图 _______________________ 2到杆的距离小,则 由平行四边形定则可知,合场强斜向左下 B( )
3、4处场强 _________________________ 两杆在3处的场强如图所示 由题意可知, 3处合场强大小为 同理可得3、4处合场强方向相同 C()D( )
专题八 静电场
考向一 电场力的性质
2025年高考物理专题复习资料
考点切片
考点1 电荷守恒定律和库仑定律
1.(2024山东济南期末)三个完全相同的带电导体球、、,带电荷量分别为 、
0和,让与先接触,然后让与接触,最终 所带的电荷量为( )
A
A. B. C. D.
【解析】 三个带电导体球完全相同,根据电荷守恒定律得,与 先接触后两球带
电荷量均为,再让与 接触,两球最终带电荷量均为
(【点拨】完全相同的导体球接触后带电荷量先中和再平分。)。
. .
. .
2.(2025湖北名校联考)如图,将不计重力、电荷量为的带负电的小圆环套在半径为
的光滑绝缘半圆弧上,半圆弧直径两端的点和 点分别固定两负点电荷。将小圆环从
靠近点处由静止释放,当小圆环运动至点时动能最大,已知 ,则( )
B
A.、两电荷所带电荷量之比为
B.、两电荷所带电荷量之比为
C.小圆环从点运动到 点的过程中静电力先做正功再
做负功
D.小圆环从点运动到 点的过程中静电力先做负功再
做正功
【解析】 小圆环运动至 点时动能最大
(【点拨】小圆环在过 的切线方向上合外力为零。),
且小圆环与两点电荷均带负电,可知在 点时,两点电
荷对小圆环的静电力的合力的反向延长线过圆心,与此
时小圆环速度方向垂直,如图所示,根据几何关系有,
小圆环重力不计,由于小圆环从靠近 点处由静止释放,动能与电势能之和守
恒,当小圆环运动至点时动能最大,表明在 点小圆环的电势能最小,所以小圆环从
点运动到 点的过程中电势能一直减小,所以静电力一直做正功。
由库仑定律有, ,解得
。
3.(2024湖南长沙长郡中学检测)如图所示,绝缘水平天花板上的 点用绝缘丝线悬挂
一电荷量为的小球,丝线长为,在同一水平线距离点处固定另一电荷量为
的点电荷(,大小未知)。当小球静止时,丝线和竖直方向间的夹角 ,
已知小球的质量为,重力加速度为,静电力常量为 ,小球可视为质点,下列说法
正确的是( )
C
A.丝线的拉力大小为
B.两带电体间的相互作用力为
C.
D.由于漏电,电荷量 减小时,丝线的拉力不变
【解析】 第一步:画出受力分析图,找各力之间关系。
设小球和点电荷间的库仑力为,小球 受力情况如图所示,由几何关系可知
,再结合力的矢量运算可得两带电体间的相互作用力 ,丝线的拉力
。
根据库仑定律有,解得 。
第二步:找出相似三角形。
设过点的竖直线与、连线的交点为,、间距离为,由于漏电,电荷量 减
小时,小球将下移,故 变大,由力的分析图可知三力组成的矢量三角形和三角形
相似,根据相似三角形对应边比值相等可得,当 变大、丝线长度不变时,
丝线的拉力减小。
考点2 电场强度
题组1 电场的基本性质
4.(2024浙江宁波期中)用两根长度相等的绝缘细线系住两个质量相等的带电小球 和
,带正电,带负电,且 ,悬挂在水平向右的匀强电场中,保持平衡状
态,能正确表示系统平衡状态的图是( )
C
A. B. C. D.
【解析】 设,带正电,受到的电场力水平向右, 带负电,受
到的电场力水平向左。以整体为研究对象,设、间的细线与竖直方向的夹角为 ,
则由平衡条件得;以小球为研究对象,受力如图所示,设、 间的细线
与竖直方向的夹角为 ,则由平衡条件得,可得 。
5.(2024吉林通化期末)如图所示,长为 、不可伸长的绝缘细线一端系一质量为
的可视为质点的带电小球,另一端悬挂在 点,当空中存在水平向右、大小
为的匀强电场时,小球偏转 后在点处于静止状态。 ,
,重力加速度取 。
(1) 分析小球的带电性质及带电荷量;
【答案】 正电;
【解析】 设小球的质量为,带电荷量为,电场强度大小为 ,细线
的拉力为 ,对小球进行受力分析,因小球静止,故受力情况如图所示,
因小球所受电场力方向与电场方向同向,故小球带正电。小球受力平衡,
则有
(2) 求细线的拉力大小;
【答案】
【解析】 根据受力分析图可知 。
解得 。
(3) 改变电场强度的大小和方向,为使小球仍保持静止在 点,求电场强度的最小值
和方向。
【答案】 ; 方向垂直于 斜向右上方
【解析】 重力、细线的拉力和电场力三力可构成闭合矢量三角形。重力的大小、方向
均不变,细线拉力方向不变,由几何关系可知,当电场力的方向与细线的拉力方向垂直
时,电场力取最小值,电场强度最小,设为 ,则
解得
方向垂直于 斜向右上方。
题组2 电场强度 电场强度的叠加
解题觉醒
1.题型特征
(1)三点法:匀强电场中,已知几何关系和三点电势,求电场强度的方向和大小。
(2)正交分解法:匀强电场中,已知几个点的电 势或电势差,题图有垂直关系,求电场强度。
(3)割补法:空间存在多个点电荷,图形对称,某位置电荷量不同,求电场强度。
2.解题步骤
(1)三点法:①找电势相等的点;②连等势线;③作等势线的垂线;④求电场强度。
(2)正交分解法:①找到两条垂直线段;②根据电势差、距离计算两个分电场强度;
③使用勾股定理计算合电场强度。
(3)割补法:通过割补,灵活构造对称,进而利用对称性和矢量叠加法,结合点电荷
场强公式求电场强度。
6.[多选](2024湖南永州月考)如图所示,在匀强
电场中建立直角坐标系,原点的电势为, 点坐
标为,电势为,点坐标为 ,
电势为 ,则该电场的电场强度
( )
BC
A.方向与轴正向成 向右上方
B.方向与轴负向成 向左下方
C.大小为
D.大小为
【解析】 运用大招46三点法求电场强度。如图所示。
第一步:找三点的最低点和最高点。
连接、两点,取的中点,可得点的电势为,与 点相同。
第二步:找等势线。
连接、两点,线段 即为等势线。
第三步:作等势线的垂线。
过点作等势线的垂线交于点,即为电场线,方向为由点指向 点,由几何
关系可知,与轴负方向的夹角为 。
第四步:求出电场强度大小。
由几何关系可知,、两点的电势差为 ,可求出匀强电场的电场强度
大小为 。故选B、C。
跳跳学长传妙招
已知三点电势求场强的方法
等分法 平行结论法 正交分解法
_____________________________________ ___________________________________ ___________________________________
匀强电场中同一条直线 上的线段两端点间电势 差正比于线段长度 匀强电场中,若两线段平行,则这 两线段各自的端点间电势差正比于 线段长度。题中出现平行线时可用 此方法 匀强电场中利用 ,
分别求出两垂直方向的场
强,再求出合场强
7.(2024湖南邵阳模拟)一圆心在点、半径的半圆,为其直径, 是半圆
上的一点, ,半圆所在的平面内有一匀强电场,、、 三点的电势分别
为、、。已知, ,则下列说法
正确的是( )
C
A.该匀强电场的电场强度的方向与直径的夹角为
B.该匀强电场的电场强度的方向与直径的夹角为
C.该匀强电场的电场强度大小为
D.该匀强电场的电场强度大小为
【解析】 题图中有垂直关系 ,运用正交分解法求电场强度。
第一步:如图所示,找到两条垂直线段和 。
, ,, 。
第二步:根据电势差、距离计算两个分电场强度。
, 。
第三步:使用勾股定理计算合电场强度。
, ,电场强度的方向沿半径 方向,
即电场强度方向与直径的夹角为 。
8.(2024河北卷)如图,真空中有两个电荷量均为
的点电荷,分别固定在正三角形的顶点 、
。为三角形的中心,沿 的中垂线对称放置一根
与三角形共面的均匀带电细杆,电荷量为 。已知正三角
形的边长为,点的电场强度为0,静电力常量为 。
顶点 处的电场强度大小为( )
D
A. B. C. D.
【解析】 第一步:由点电荷场强公式及场强的叠加计算、点的电荷在 点的场强
B、点的电荷在的场强的合场强为 。
第二步:计算带电细杆在 点的场强
点的合场强为零,因此带电细杆在点的场强大小 。
第三步:由对称性及场强叠加计算 点的场强
由对称性可知,带电细杆在点的场强大小为,方向竖直向上,因此 点处
的合场强为 ,D项正确。
9.(2024云南昆明一中模拟)均匀带电的球
壳在球外空间产生的电场等效于电荷集中于
球心处的点电荷产生的电场。如图所示,在
绝缘球球面 上均匀分布正电荷,总
C
A. B. C. D.
电荷量为;在剩余球面上均匀分布负电荷,总电荷量是。球半径为 ,球心为
,为球面的对称轴,在轴线上有、两点,且 ,
,。已知球面在点的场强大小为,静电力常量为 ,
则 点的场强大小为( )
【解析】 将 部分补上,使球壳变成一个均匀带正电的完整的球壳,完整球壳带电荷
量为,为保证电荷量不变,球面带负电荷量为,则该球壳带正电的部分在
点产生的场强为,根据对称性可知:①带正电的部分完整球壳在 点产
生的场强大小;②球面带负电荷量为,在点产生的场强大小为 ,两者
方向相反;则点的场强大小为 ,故选C。
10.(2024湖南名校联考)理论分析表明,一根长为 的均匀带正
电的细杆竖直放置,当时,细杆两端处的场强 ,
细杆中间处的场强。其中为常数, 为电荷线密度
(细杆带电荷量与长度的比值), 为点到细杆的垂直距离,如图
甲所示。若再取一根与完全一样的均匀带正电细杆 ,平行放置
在的右侧,距离为 ,如图乙所示。它们端点的连线上
A
A.1处合场强大小为 B.2处合场强方向竖直向下
C.3处合场强大小为 D.3、4处合场强方向不同
有点1、2、3、4,其中1、3到杆的距离均为,各点到两杆的距离均远小于杆长 。关
于各点场强的大小与方向,下列说法正确的是( )
【解析】
题干分析 将细杆中间断开看成两根细杆,则中间点的场强为 ,可 得 ,即细杆在两端的场强的方向与水平方向的夹角为 1处场强如图 _______________________ 1到、两杆的距离均为 则1处的合场强为 A(√)
2处场强如图 _______________________ 2到杆的距离小,则 由平行四边形定则可知,合场强斜向左下 B( )
3、4处场强 _________________________ 两杆在3处的场强如图所示 由题意可知, 3处合场强大小为 同理可得3、4处合场强方向相同 C()D( )
同课章节目录
