考向二 动量守恒定律及其应用-2025年高考物理专题复习课件

(共139张PPT)
专题七 动量
考向二 动量守恒定律及其应用
2025年高考物理专题复习资料
考点切片
考点1 动量守恒定律的理解和基本应用
1.［多选］（2024陕西宝鸡三模）如图所示，竖直墙面和水平
地面均光滑，质量分别为、的、 两物体
用质量不计的轻弹簧相连且静止，其中紧靠墙面。现对 物
BC
A.撤去外力后，两物体和弹簧组成的系统动量守恒
B.撤去外力后，两物体和弹簧组成的系统机械能守恒
C.从撤去外力至与墙面刚分离，弹簧对的冲量 ，方向水平向右
D.与墙面分离后弹簧首次恢复原长时，两物体速度大小均是 ，方向相反
体缓慢施加一个向左的力，使、 间弹簧被压缩且两物体和弹簧组成的系统静止，该
力对物体做的功 。现突然撤去向左的力，则( )
【解析】 撤去外力后，在弹簧首次恢复原长的过程中，墙对 物体有弹力的作用，
所以两物体和弹簧组成的系统动量不守恒，弹簧首次恢复原长后，系统动量才守恒。
撤去外力后，系统内只有动能和弹性势能互相转化，机械能守恒。
压缩弹簧时，外力做的功完全转化为弹性势能。撤去外力后，弹簧首次恢复原长，
弹性势能完全转化为的动能，则有，代入数据可得 ，由
动量定理可知弹簧对的冲量大小 ，方向水平向右。
刚与墙面分离时，弹簧恢复原长，此时速度最小，为0。、都运动后， 减
速，加速。、速度相等时弹簧拉伸最长。此后一段时间，继续减速， 继续加速，
弹簧拉伸量减小，再次恢复原长时，设向右为正方向，由机械能守恒定律和动量守恒定
律可知，，解得 ，
。
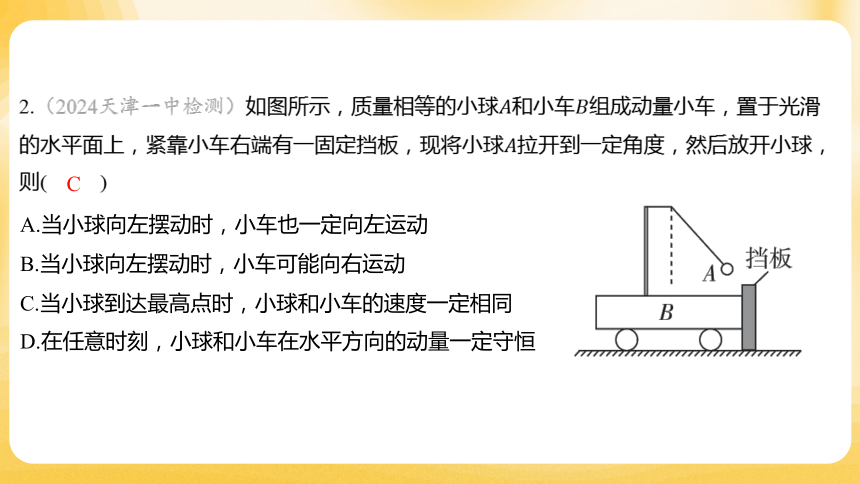
2.（2024天津一中检测）如图所示，质量相等的小球和小车 组成动量小车，置于光滑
的水平面上，紧靠小车右端有一固定挡板，现将小球 拉开到一定角度，然后放开小球，
则( )
C
A.当小球向左摆动时，小车也一定向左运动
B.当小球向左摆动时，小车可能向右运动
C.当小球到达最高点时，小球和小车的速度一定相同
D.在任意时刻，小球和小车在水平方向的动量一定守恒
【解析】 当小球从右向左摆动到最低点的过程中，细线对小车的拉力沿右下方，
由于有挡板，小车不动，此过程中小球和小车组成的系统在水平方向动量不守恒；当小
球向左摆动经过最低点继续向左运动时，细线对小车的拉力沿左下方，则小车向左运动，
此过程中小球和小车组成的系统在水平方向动量守恒，当小球到达最高点时，小球和小
车的速度一定相同。
跳跳学长有话说
通过对小车的受力分析及状态分析，确定小车是否受到挡板的作用力，进而确定、 组
成的系统在水平方向是否受外力作用，最终确定系统在水平方向上动量是否守恒。若系统
在水平方向上动量守恒，则可在水平方向上依据动量守恒确定小球与小车的运动状态。
考点2 反冲模型
3.（2024江苏海门中学模拟）如图所示，一架总质量为 （含燃料）的飞船在太空中以
速度匀速航行，某时刻飞船在极短的时间内喷射出质量为 的燃烧气体，气体喷出后
与飞船的相对速度大小为 ，设飞船初始运动方向为正方向，则( )
B
A.气体对飞船的冲量小于飞船动量的变化量
B.气体喷出后的运动方向可能与飞船运动方向相同
C.和 的比值越大，飞船速度的增加量就越小
D.飞船喷出气体后速度可增加到
【解析】 根据动量定理可知，气体对飞船的冲量等于飞船动量的变化量。
当飞船的速度大于气体相对飞船的速度时，气体喷出后的运动方向与飞船运动方
向相同。
取飞船初始的运动方向为正方向，由动量守恒得
（【易错】同一系统内各部分动量的参考系统一，必
须为同一参考系。），可得，和 的比值越大，飞船速度的增加量就
越大。
. .
4.（2024安徽淮北二模）北京时间2024年3月2日，神舟十七号航天员汤洪波、唐胜杰、
江新林密切协同，在地面科研人员的配合支持下，进行了约8小时的出舱活动，完成既
定任务。为了保证出舱航天员的安全，通常会采用多重保障，其中之一就是出舱航天员
要背上可产生推力的便携式设备，装备中有一个能喷出气体的高压气源。假设一个连同
装备共有的航天员，脱离空间站后，在离空间站 的位置与空间站处于相对静
止的状态。航天员为了返回空间站，先以相对空间站的速度向后喷出 的
气体，距离空间站 时，再次以同样速度喷出同等质量的气体，则航天员返回空间
站的时间约为( )
B
A. B. C. D.
【解析】 设航天员的速度方向为正方向，第一次喷气后航天员的速度为 ，则根
据动量守恒定律得 ，即
，解得，此 所需的时间
为。再次喷气，设喷气后航天员的速度为 ，根据动量守恒定律
有 ，即
，解得
，此后所需的时间为 ，则航天员返回空间站的
时间约为 。
考点3 人船模型
解题觉醒
1.题型特征：初始时人和船均静止，人在船上走，人在往前走的过程中船会往后走，求
一段时间后人和船的速度、位移大小。
2.解题技巧：
（1）速度关系：。
（2）位移关系：,。
5.（2024辽宁本溪期末）如图所示，质量为的人，站在质量为 的车的一端。
车长为 ，开始时人、车相对于水平地面静止，车与地面间的摩擦可忽略不计。当人
由车的一端走到另一端的过程中，下列说法正确的是( )
D
A.人的速率最大时，车的速率最小
B.人的动量变化量和车的动量变化量相同
C.人对车的冲量大小大于车对人的冲量大小
D.当人走到车的另一端时，车运动的位移大小为
【解析】 运用大招人船模型进行解题。人在运动过程中人与车组成的系统动量守
恒，则 ，可知人的速率最大时，车的速率也最大。
由动量定理可知，动量变化量的方向与合外力的方向相同，而车与地面间的摩擦
忽略不计，车对人的摩擦力与人对车的摩擦力方向相反，故人的动量变化量和车的动量
变化量大小相等，方向相反。
人对车的作用力和车对人的作用力为相互作用力，则人对车的冲量大小等于车对
人的冲量大小。
设车移动的距离为，则由动量守恒定律有 （【点拨】由大招人船
模型核心方程，变形得出。），解得 。
. .
6.（2024湖南部分学校三模改编）某科技馆内有一用来观察摆球与牵连配重滑块运动规
律的装置，如图所示，一穿套有质量为 的带孔滑块的足够长的光滑轨道杆水平固定
在水平地面上方，一不可伸长的轻质细绳一端固定在滑块下方 点，另一端连接质量为
的小球。已知绳长为，水平杆距地面足够高，当地重力加速度为 ，忽略空气阻力。
将轻质细绳伸直，小球从点（点与 点等高且在水平杆正下方）静止释放。当小球第
一次摆动到最低点时，求滑块的位移大小和此时细绳对小球的拉力大小。
【答案】 ;
【解析】 设小球摆到最低点时速度大小为，滑块速度大小为
水平杆光滑，根据水平方向系统动量守恒有，所以
（类比“人船模型”可列出滑块和小球的位移关系方程 ）。
联立可求得
根据系统机械能守恒，从释放小球到第一次到达最低点，有
解得，
对小球根据牛顿第二定律有 （【点拨】小球相对滑块做匀速圆周运
动，故列式时应使用小球相对滑块的速度。）
联立解得 。
. .
. .
考点4 爆炸模型
7.（2024陕西榆林阶段练习）冲天炮（如图）飞上天后会在天空中爆炸。当冲天炮从水
平地面斜飞向天空后且恰好沿水平方向运动的瞬间，突然炸裂成一大一小的、 两块，
且质量较大的 仍沿原来方向飞出去，不计空气阻力，则下列说法正确的是( )
B
A.炸裂前后瞬间，总动量不守恒 B.、 同时落回地面
C.炸裂后，飞行的水平距离较大 D.炸裂时，、 受到的内力的冲量相同
【解析】 炸裂时，冲天炮位于最高点，水平方向不受外力作用，动量守恒，
因此，、 的速度方向均沿水平方向，之后做平抛运动回到地面，故同时落地。
炸裂后，质量较小的 可能仍沿原来的方向运动，也可能与原运动方向相反，无法
确定、 炸裂后速度的大小关系，也就无法比较飞行的水平距离大小关系。
炸裂时、受到的内力大小相等，方向相反，故炸裂时、 受到的内力的冲量大
小相等，方向相反。
8.一质量为的烟花弹以初速度 从水平地面竖直向上射出，上升到最大高度时恰好爆
炸，沿水平方向分裂成质量之比为的、两个部分，此时、 动能之和与烟花弹
从地面射出时的动能相等。爆炸时间极短，不计空气阻力，则( )
C
A.烟花弹从射出到爆炸后瞬间的过程中，机械能守恒
B.爆炸过程释放的能量与、 落地时的总动能相等
C.、两部分落地时速度大小之比为
D.、两部分落地时速度大小之比为
【解析】 烟花弹从射出到上升到最大高度的过程中只有重力做功，机械能守恒；
烟花弹爆炸过程中，重力势能不变，动能增加，故机械能增加。
爆炸过程释放的能量等于爆炸结束瞬间、的动能之和，小于、 落地时的总动
能。
设、的质量分别为、 ，则爆炸过程中由动量守恒定律可得
（【提醒】由于爆炸是在极短的时间内完成的，发生爆炸的物体之间的相
互作用力远远大于受到的外力，所以在爆炸过程中，系统的总动量守恒。），解得
，设，由题意可知， ，解得
，则，，烟花弹爆炸后、 两部分做平抛运动，水平分速度大小
. .
. .
分别为、，落地时的竖直分速度大小均为，则落地时地 ，
地，所以、两部分落地时速度大小之比为 。
考点5 碰撞
题组1 非弹性碰撞
解题觉醒
1.完全非弹性碰撞题型特征：碰后两物体共速，计算碰后机械能损失。
2.运用折合质量法解题步骤：
（1）确认是否满足使用条件，即碰后是否共速；
（2）利用质量、碰前速度计算、；
（3）代入计算碰后的机械能损失。
9.（2024安徽合肥期中）如图所示，在光滑水平面上，一质量为的球，以
的速度向右运动，与质量为、大小相同的静止的球发生对心碰撞，撞后 球的速
度大小为，取 球初速度方向为正方向，下列说法正确的是( )
D
A.该碰撞为弹性碰撞
B.该碰撞为完全非弹性碰撞
C.碰撞前后球的动量变化量为
D.碰撞前后球的动量变化量为
【解析】 以 球初速度方向为正方向，碰撞过程根据动量守恒可得
，解得球碰后的速度为，碰撞前后 球的动量变
化量为 。
碰撞前系统的机械能为 ，碰撞后系统的机
械能为 ，由于
，且碰后、 速度并不相同，则该碰撞不是弹性碰撞，也不是完全非弹性碰撞。
质量为的小球以速度碰质量为 的静止小球，若要判断碰撞
是弹性碰撞还是非弹性碰撞，也可以使用不等式
来判断，当两边的不等
号取等时，该碰撞是弹性碰撞；当中间的两个不等号取等时，该碰撞是完全非弹性碰撞；
当四个不等号都没有取等时，该碰撞是非弹性碰撞，但不是完全非弹性碰撞。
——江苏省启东中学 孙家浩
10.（2024山东烟台一模）如图所示，某超市两辆相同且质量均为、相距 的手推购
物车沿直线排列，静置于水平地面上。为节省收纳空间，工人给第一辆车一个瞬间的水
平推力 使车自行运动，并与第二辆车相碰，且在极短时间内相互嵌套结为一体，以共
同的速度运动了，恰好停靠在墙边。若车运动时受到的摩擦力恒为车重力的 倍，忽略
空气阻力，重力加速度为。则工人给第一辆购物车的水平推力 的冲量大小为( )
A
A. B. C. D.
【解析】 设第一辆车碰前瞬间的速度为，与第二辆车碰后的共同速度为 ，由
动量守恒定律有，根据动能定理可得 ，联立解
得。设第一辆车推出时的速度为 ，根据动能定理可得
，解得 。根据动量定理可知，工人给第一辆购
物车水平推力的冲量大小为 。
11.（2023天津卷）已知、两物体的质量，，物体从
处自由下落，且同时物体从地面竖直上抛，经过 相遇。碰撞后，两物体立刻
粘在一起运动，取 ，求两物体：
（1） 碰撞时离地高度 ；
【答案】
【解析】 对物体 ，根据运动学公式可得
。
（2） 碰后速度 ；
【答案】 0
【解析】 设物体从地面竖直上抛的初速度为 ，根据运动学公式可知
即
解得
碰撞前瞬间物体的速度大小为 ，方向竖直向下
碰撞前瞬间物体的速度大小为 ，方向竖直向上，选向下为正方
向，由动量守恒定律可得
解得碰后速度 。
（3） 碰撞损失的机械能 。
【答案】
【解析】 根据能量守恒可知碰撞损失的机械能
(【大招运用】计算损失的机械能可直接
运用大招， 。)。
. .
题组2 弹性碰撞
解题觉醒
1.题型特征：碰撞过程中没有能量损失。
2.解题技巧：每个碰撞物体的碰前速度、两物体发生完全非弹性碰撞的共同速度、碰后
速度，这三个速度的数值均成等差数列。如、两球分别以速度、发生弹性碰撞，
碰后速度分别为、。若两球发生完全非弹性碰撞，碰后两球共同速度为，则
，。
3.解题步骤：
（1）判断是否发生弹性碰撞；
（2）计算出碰前总动量，根据计算；
（3）利用等差数列求解碰后速度。
12.［多选］（2024福建漳州二模）如图，冰壶被大家喻为冰上的“国际
象棋”，它考验参与者的体能与脑力，展现动静之美，取舍之智慧。质
量相同的冰壶甲和乙相距，冰壶甲以速度 被推出后做匀减速直
线运动，经过 与静止的冰壶乙发生对心弹性碰撞，则( )
BD
A.两冰壶碰撞后均向前运动 B.两冰壶碰撞后，甲静止不动
C.冰壶甲初速度大小可能为 D.冰壶甲初速度大小可能为
【解析】 根据两质量相等的物体，发生弹性碰撞后交换速度可知，两冰壶碰
撞后，甲静止不动，乙向前运动。
冰壶甲碰撞前做匀减速直线运动，则 ，由题意可知
，代入数据得，但如果，则，即 ，
与甲做匀减速运动矛盾。
13.（2024贵州部分地区模拟）如图，光滑水平地面上，动量为 的小球1向右运动，与
同向运动且动量为的小球2发生弹性碰撞，，碰撞后小球1的速度为 、动能
为、动量大小为，小球2的速度为、动能为、动量大小为 。下列选项一
定正确的是( )
D
A. B.碰撞后球2向右运动，球1向左运动
C. D.
【解析】 小球1与小球2发生碰撞，则两小球的速度关系满足 ，可得
，根据两个物体发生弹性碰撞的碰后速度公式可得碰撞后瞬间两小球的速度分
别为
， （【大招运用】根据
大招内容速度增量法可得 ，
），因此当足够大时可使 ，
当 时可使碰后两者都向右运动。
. .
碰撞过程小球2动能增大（【点拨】小球2作为被碰的一方，碰后速度增大，方向
不变。），由动量与动能的关系 可知小球1的初动能大于小球2的初动能，故碰
后动能大小不确定。
碰撞过程小球2动量增大，且系统动量守恒，所以 。
14.（2025湖北名校联盟阶段练习）如图所示（俯视图），
光滑水平面上放置着内侧表面光滑的半圆弧挡板，两个可
视为质点的小球、 可沿半圆弧挡板内侧在水平面内做
圆周运动，、两球的质量分别为 、
，半圆弧挡板半径为 。半圆弧挡板的一
端安装有一个弹射器， 球与其碰撞后可原速率弹回。初
始时，球静止放在半圆弧挡板的最左端， 球以
（1） 球和球第一次碰撞前，半圆弧挡板对球支持力 的大小；
【答案】
【解析】 对根据牛顿第二定律得
解得 。
的速度从另一端沿水平方向进入半圆弧运动，并与 球发生弹性碰撞。求：
（2） 球和球第一次碰撞后，二者速度、 的大小；
【答案】 ;
【解析】 、 第一次碰撞，分别由动量守恒定律和能量守恒定律得
解得， 。
（3） 球和球第二次碰撞后，二者速度、 的大小。
【答案】 ;
【解析】 、第二次碰撞，以 球运动方向为正方向，分别根据动量守恒定律和能量
守恒定律得
解得，（【大招运用】、 发生的碰撞是弹性碰撞，可用
大招求解碰后速度，，则 ，
。）
即、的大小分别为和 。
. .
题组3 碰撞可能性问题
15.［多选］质量为的物块以某速度运动与质量为的静止物块 发生正碰，碰撞后
两者同向运动且的动量是的两倍，两者质量与 的比值可能为( )
BC
A.1 B.3 C.5 D.7
【解析】 以、组成的系统为研究对象，碰撞过程中，系统动量守恒，以
的初速度方向为正方向，由动量守恒定律得，碰撞后 的动量大小正
好是的动量大小的两倍，则有，解得, 。碰撞过程，机械
能不增加，则有,联立解得；其次碰撞后 的速度不大于
的速度，有,解得,联立可得 。
跳跳学长 敲黑板
碰撞可能性的主要判断依据：（1）碰撞过程，机械能不增加；（2）追碰问题，碰撞
前，；碰撞后， 。
16.（2024河北保定阶段练习）如图所示，质量为的小球 静止在光滑水平地面上，
质量为的小球以速度向小球运动，两小球发生正碰后，小球的动能用 表示，
小球的动能用 表示，则下列表达式可能正确的是( )
A
A. B. C. D.
【解析】 若两小球发生弹性碰撞，根据动量守恒有 ，根据机
械能守恒有，解得， （【大招运用】运用大
招内容速度增量法可得 ）。若两小球发生完全
非弹性碰撞，根据动量守恒有，解得。所以碰后小球 的速度
满足，小球的速度满足，所以 ，
。
. .
题组4 多次碰撞问题
17.［多选］（2025湖北黄石阶段练习）如图所示，一个固定斜面与水平地面平滑连接，
斜面与水平地面均光滑。小物块放在水平地面上，小物块 自斜面上某位置处由静止
释放，、 之间的碰撞为弹性正碰，斜面与水平面足够长，则下列说法正确的是
( )
AC
A.若，则、 只能发生一次碰撞
B.若，则、 只能发生一次碰撞
C.若，则、 只能发生两次碰撞
D.若，则、 只能发生三次碰撞
【解析】 设滑到水平面上时速度大小为，、 发生弹性正碰，动量守恒
及总动能不变，有， ，联立解得第
一次碰后， （【点拨】一个物体与另一个静止的物体发生
弹性碰撞，碰后速度公式大家要记牢，用到得非常多。）。若，则碰后 滑上
斜面并返回，到达水平地面的速度与发生碰撞后的速度等大反向，若不能追上 ，则
有，解得 。
同理，若，第一次碰后，，之后滑上斜面并返回，
从斜面返回水平面后速度为， ，
. .
. .
， （【大招运用】运用大招可快速求出
、第二次碰后的速度。）。故、 只能发生两次碰撞。
若，第一次碰后，，之后 滑上斜面并返回，运用大招
求出与发生第二次碰撞后，、的速度分别为，，故、 只能
发生两次碰撞。
. .
跳跳学长 敲黑板
由弹性碰撞的结论确定碰撞后两物体的速度，若碰后物块的速率大于物块 的速率，
则可以发生下一次碰撞，直到碰后物块的速率小于或等于物块 的速率。
18.设问创新［多选］（2024山东青岛五十八中模拟）如图所示，固定光滑曲面左侧与光滑水平面
平滑连接，水平面依次放有100个质量均为的物块（所有物块在同一竖直平面内），质量为
的0号物块从曲面上高处静止释放后沿曲面滑到水平面，以速度 与1号物块发生碰撞，0号物块
反弹后滑上曲面再原路返回，如此反复，假设所有碰撞都是弹性碰撞，所有物块均可视为质点，
重力加速度为 ，则下列说法正确的是( )
BC
A.100号物块最终动量大小为
B.0号物块第二次反弹后沿斜面上升的高度为
C.0号物块最终速度大小为
D.0号物块最后一次与1号物块碰撞后至再次返回
水平面的过程，曲面对0号物块作用力的冲量大
小为
【解析】 对0号物块，根据机械能守恒定律有，解得 ，0
号物块与1号物块发生弹性正碰过程，由动量守恒定律和机械能守恒定律有
，，解得 ，
， 号物块两两之间碰撞时交换速度，所以100号物块最终速度是0
号物块与1号物块发生弹性正碰后1号物块的速度，100号物块的最终动量大小为
。
号物块第二次与1号物块发生碰撞时的速度大小为 ，碰撞规律与第一次碰
撞规律相同，则碰后速度为，根据机械能守恒有 ，解
得 。
根据以上分析规律可知最终碰撞结束时，0号物块的速度大小为
（【点拨】0号物块第一次与1号物块碰后，100号物块以“交换速度”向左运动，当0号物
块第二次与1号物块碰撞后，99号物块以下一“交换速度”向左运动，以此类推，当0号物
块第100次与1号物块相碰后，1号物块也将向左运动。最终100号物块到0号物块均向左
运动，且速度依次减小。）。
号物块最后一次与1号物块碰撞后至再次返回水平面的过程，0号物块的动量变化
量的大小为 ，根据动量定理，曲面的作用力和重力的合力对0号物
块的冲量大小为 。
. .
19.（2023全国乙卷）如图所示，一竖直固定的长直圆管内有一质量为 的
静止薄圆盘，圆盘与管的上端口距离为，圆管长度为 。一质量为
的小球从管的上端口由静止下落，并撞在圆盘中心，圆盘向下滑
动，所受滑动摩擦力与其所受重力大小相等。小球在管内运动时与管壁不
接触，圆盘始终水平，小球与圆盘发生的碰撞均为弹性碰撞且碰撞时间极
短。不计空气阻力，重力加速度大小为 。求：
（1） 第一次碰撞后瞬间小球和圆盘的速度大小；
【答案】 ;
【解析】 设碰撞前瞬间小球的速度为，碰后瞬间小球和圆盘的速度分别为、 ，取
竖直向下为正方向，对碰撞前，小球自由下落的过程，由动能定理得
解得
小球和圆盘碰撞过程满足动量守恒和机械能守恒，有
又
联立解得， 。
（2） 在第一次碰撞到第二次碰撞之间，小球与圆盘间的最远距离；
【答案】
【解析】 在第一次碰撞到第二次碰撞之间，小球先向上做匀减速直线运动，到最高点
再向下做匀加速直线运动，圆盘一直向下做匀速直线运动，当小球速度向下且与圆盘速
度相等时，两物体间距最大，设此过程所经历的时间为 ,对小球，由匀变速直线运动公
式得
解得
由竖直上抛运动的对称性知，此时小球又回到了与圆盘第一次碰撞的位置，故圆盘下落
的距离就是此时小球与圆盘的间距，也是在第一次碰撞到第二次碰撞之间小球与圆盘的
最远距离，为
。
（3） 圆盘在管内运动过程中，小球与圆盘碰撞的次数。
【答案】 4
【解析】 设小球和圆盘从第一次碰撞后瞬间到第二次碰撞前瞬间经历的时间为 ，有
解得
在这段时间内，圆盘下落的距离为
设小球第二次与圆盘碰撞前瞬间速度为 ，则
设第二次碰后小球和圆盘的速度分别为、 ，小球和圆盘碰撞过程满足动量守恒和
机械能守恒，有
解得，（【大招运用】运用大招列 ,
，，可快速计算、 。本题涉及多次计算碰后速度问
题，且碰撞为弹性碰撞，可直接运用速度增量法求碰后速度。）
设小球和圆盘从第二次碰撞后瞬间到第三次碰撞前瞬间经历的时间为 ，有
解得
在这段时间内圆盘下降的距离为
同理，小球第三次与圆盘碰撞前瞬间速度为
小球与圆盘发生第三次碰撞，由动量守恒和系统能量守恒有
. .
解得，
设经过 ，小球与圆盘发生第四次碰撞，有
解得
在这段时间里，圆盘下降的距离为
由数学归纳法知（【点拨】计算出每次碰撞的时间间隔和圆盘下降的距离，分析其中的
规律，得出后续运动过程中的物理量。），以后每次碰撞间隔时间均为 ，在这段时
间内圆盘下降的距离比上次碰撞间隔内下降的距离增加 ,所以从第四次碰撞后瞬间到
第五次碰撞前瞬间，圆盘下降的距离为 ,若圆盘始终在管内运动，则从第一次碰撞后
瞬间到第五次碰撞前瞬间，圆盘下降的距离为 ，故此
时圆盘已经滑出长直圆管，不会在管内发生第五次碰撞，所以圆盘在管内运动过程中，
小球与圆盘碰撞四次。
跳跳学长 有话说
考点6 4种典型的碰撞模型
题组1 子弹打木块模型
解题觉醒
1.解题技巧：子弹打木块模型类似板块模型。子弹相当于物块，木块相当于板。
2.若地面光滑，子弹留在木块中，对木块、子弹整体列动量守恒方程和能量守恒方程。
（1）求子弹射入木块过程系统损失的机械能，运用折合质量法求解。
（2）求最终子弹进入木块的深度，根据求解。
20.设问创新（2023北京八中期末）质量为的木块静止放在光滑的水平面上，质量为
的子弹以速度 沿水平方向射中木块并最终留在木块中与木块一起运动。不考虑子弹的
重力，当子弹恰与木块相对静止时，子弹和木块的初、末位置的示意图正确的是( )
C
A. B. C. D.
【解析】 设当子弹恰与木块相对静止时，木块前进
的距离为，子弹进入木块的深度为 ，木块和子弹的共同
速度为 。子弹射入木块过程，取向右为正方向，根据动
量守恒定律得 ，对子弹，根据动能定理
有 ，对木块，根据动能定理有
【另解】当子弹恰与木块相对静止时，设木块前进的距离为 ，子弹进入木块的深度为
，子弹与木块的速度—时间图像如图所示，显然子弹射入木块的深度 大于木块的位移，
C正确。
，联立解得, ，
故，则，比较四个选项中与 的大小关系。
21.（2024北京海淀区模拟）如图所示，用长为的轻绳悬挂一质量为 的沙箱，沙箱静
止。一质量为的弹丸以速度 水平射入沙箱并留在其中，随后与沙箱共同摆动一小角
度。不计空气阻力。对于子弹射向沙箱到与其共同摆过一小角度的过程，下列说法正确
的是( )
C
A.整个过程中，弹丸和沙箱组成的系统动量守恒
B.子弹击中沙箱到与沙箱共速的过程机械能守恒
C.若保持、、不变， 变大，则系统损失的机械能变大
D.若保持、、不变， 变大，则弹丸与沙箱的最大摆角不变
【解析】 弹丸击中沙箱过程系统水平方向动量守恒，而系统的机械能因摩擦
生热而减少，弹丸与沙箱一起摆动过程系统所受合外力不为零，动量不守恒，故整个过
程中弹丸和沙箱组成的系统动量不守恒。
以弹丸的初速度方向为正方向，由动量守恒定律得 ，解得
,由能量守恒定律可知，整个过程系统损失的机械能为
(【大招运用】可用折合质量法计算出结果
)，若保持、、不变， 变大，则系统损失的机械能变大。
弹丸与沙箱一起摆动过程，设最大摆角为 ，则有
，联立解得 ，若保持 、
、不变，变大，则弹丸与沙箱的最大摆角 变小。
. .
. .
22.（2024广东汕头期中）如图所示，一颗质量为
的子弹（可视为质点），沿水平方向射向静止在光滑水
（1） 木块获得的速度大小；
【答案】
【解析】 子弹与木块组成的系统动量守恒，以向右为正方向，由动量守恒定律得
代入数据解得木块的速度大小 。
平桌面上的木块，木块的质量为，长度为，子弹射入前速度为 ，穿
出木块时速度减为 ，已知子弹穿过木块过程中木块对子弹的阻力不变，求：
（2） 此过程中，木块对子弹的阻力大小；
【答案】
【解析】 由能量守恒定律得
代入数据解得 。
（3） 子弹穿过木块过程所用时间（结果保留3位有效数字）。
【答案】
【解析】 子弹对木块作用力的冲量等于木块动量变化量，得
由牛顿第三定律可知
代入数据解得 。
题组2 板块模型
23.（2024广西河池期末）如图所示，质量为
的长木板静止在光滑水平面上，质量
为 的物块以水平向右的初速度滑上长
（1） 当物块的初速度时，物块恰好不滑离木板，求木板长度 ；
【答案】
【解析】 物块与木板组成的系统动量守恒，可得
由动能定理可得
解得 。
木板的左端，物块与木板之间的动摩擦因数为 ，将物块视为质点，最大静摩擦
力等于滑动摩擦力，重力加速度取 。
（2） 若木板的长度为（1）中所求的长度，当物块以 的初速度滑上木板时，
同时给木板施加一个水平向右的恒力 ，求：
【解析】 ①对物块，根据牛顿第二定律可得
所以
当物块恰好滑到木板最右端时和木板速度相等，此过程中对木板根据牛顿第二定律可得
解得
当物块和木板达到共同速度，且物块与木板之间达到最大静摩擦力，此时对整体有
解得
故恒力的取值范围为 。
②对物块与木板整体，由动量定理有，
解得 。
③根据以上分析可知，当时，有
解得
当时，有
解得
当时，有
解得 。
① 要使物块不滑离木板，恒力 的取值范围；
【答案】
② 在①的情形下，物块的最终速度大小与恒力 的关系；
【答案】
③ 物块与木板因摩擦产生的热量与恒力 的关系。
【答案】 当时，；当时，；当 时，
跳跳学长有话说
板块模型的动量和能量
问题分析方法
（1）模型特点
木板初速度为零且足够长 木板有初速度且足够长，板块反向
示意图 _____________________________________________________________地面光滑 _________________________________________________________________地面光滑
木板初速度为零且足够长 木板有初速度且足够长，板块反向
图 像 __________________________________________________ __________________________________________________________
（2）处理方法：根据动量守恒和能量守恒（或动能定理）列方程求解。注意速度相等
临界条件的应用。
24.（2024海南海口三模）如图所示，质量为
的小球用长为的细绳悬挂在 点，质量为
的滑板 放置在光滑水平面上，滑板
的左端放置一质量为的物块，物块位于
点正下方处，离滑板右端 处有一竖直固定挡
板。把小球拉起到细绳水平且恰好伸直的位置，由静止释放小球，小球与物块 发
生弹性碰撞（作用时间极短），之后物块在滑板上滑行。已知小球、物块 均可视
为质点，物块与滑板间的动摩擦因数为，重力加速度为，不计空气阻力，滑板
与挡板 碰撞前后没有机械能损失。
（1） 求小球与物块碰后瞬间 的速度大小；
【答案】
【解析】 根据题意可知，小球 运动到最低点过程中，由机械能守恒定律有
解得
小球与物块 发生弹性碰撞，则有
解得， 。
（2） 求滑板与挡板碰撞前的瞬间物块 的速度大小；
【答案】
【解析】 根据题意，由牛顿第二定律，对物块有
解得
对滑板有
解得
设、共速所用时间为，则有
解得
则滑板运动的距离为
. .
可知，滑板与挡板碰撞前瞬间滑板与物块未共速，设滑板与挡板碰撞前滑板
运动的时间为（【易错】与碰后，在对的摩擦力作用下向右做减速运动， 在
对的摩擦力作用下向右做加速运动，若右侧没有挡板，、 共速后一起匀速向右运
动。所以需要判断碰到挡板时，、 是否已经共速，也就是需要判断在没有挡板的情
况下，从开始运动到共速时，向右运动的位移是否大于 与挡板的间距。），则有
解得
则滑板与挡板碰撞前瞬间，物块的速度为 。
. .
. .
（3） 要使物块始终留在滑板上，求滑板 长度的最小值。
【答案】
【解析】 过程分析：与挡板碰撞后，等速度反向，并在 的摩擦力作用下做减速运
动，在对的摩擦力作用下继续向右运动。当、 速度相等时，两者不再发生相对
运动，若此时滑到了最右端， 长度取最小值。
设滑板与挡板碰撞前，滑板的速度为 ，则有
滑板与挡板碰撞前，物块与滑板的相对位移为
滑板与挡板碰撞后，滑板速度大小不变，方向反向，当物块滑到滑板 右端时，
物块与滑板恰好共速，取向右为正方向，则有
解得
则有
则滑板长度的最小值 。
题组3 弹簧模型
解题觉醒
1.题型特征：地面光滑，两个物体，中间连接弹簧。
2.解题技巧:
（1）从原长到形变量最大：可视为两物体发生完
全非弹性碰撞的过程，用折合质量法求解弹簧最
大弹性势能 。
（2）从原长到两物体分离：可视为两物体发生弹性碰撞的过程，用速度增量法求解两
物体分离速度。
25.（2023广东揭阳检测）如图所示，将质量分别为、的、 两个
物体放在光滑的水平面上，物体处于静止状态， 的左端与一轻弹簧相连接。现在给
物体一水平向右的初速度 。
（1） 求弹簧的最大弹性势能 ；
【答案】
【解析】 弹簧被压缩到最短时，、 具有共同速度，此时弹簧有最大弹性势能，取向
右为正方向，根据动量守恒定律有
根据能量守恒定律有 （【大招运用】运用大招将弹簧压
缩到最短的过程等效为完全非弹性碰撞过程，运用折合质量法求弹性势能
。）
解得 。
. .
（2） 当物体和弹簧分离时，求物体和物体 的速度大小。
【答案】 ;
【解析】 物体 和弹簧分离时，根据动量守恒定律和机械能守恒定律有
(【大招运用】运用大招将弹簧从原长到压缩为最短再到恢复
原长过程等效为弹性碰撞过程，运用速度增量法求碰后、 的速度。
，， 。)
联立解得， 。
. .
26.（2024黑龙江省实验中学期末）如图所示，固
定在轻质弹簧两端且质量分别是 、
的两个物体、 置于光滑水平地面
上， 靠在光滑竖直墙上，弹簧处于原长状态；
（1） 子弹射入前的速度大小；
【答案】
【解析】 取向左为正方向，子弹射入时，根据动量守恒定律有
弹簧被压缩到最短时，根据机械能守恒定律有
两式联立代入数据得 。
现有一颗质量的子弹水平瞬间射入 后没有射出，然后使弹簧压缩而具有
的弹性势能，最后和 都将向右运动。求：
（2） 运动前弹簧对 （含子弹）的冲量；
【答案】 ; 方向水平向右
【解析】 根据对称性，子弹和都以大小为 的速度向左压缩弹簧，而后又以同样大
小的速度向右反弹，以向右为正方向，根据动量定理可得
代入数据可得 ，方向水平向右。
（3） 、 都向右运动过程中弹簧的最大弹性势能。
【答案】
【解析】 、都向右运动过程中，弹簧弹性势能最大时、 和子弹三者共速，有
根据能量守恒定律，此时的最大弹性势能为
代入数据解得 。
【大招运用】取子弹和从弹簧原长向右运动到弹簧最长的过程为研究过程，运用大招
可知该过程可等效为完全非弹性碰撞过程，可运用折合质量法求最大弹性势能，
。
题组4 圆弧轨道模型
解题觉醒
1.题型特征：在光滑的水平面上有一光滑的圆弧轨道，物块以某一初速度滑上圆弧轨道，
求相关物理量。
2.解题技巧：
如图所示，质量为的小球在光滑水平面上以速度滑上质量为的光滑圆弧轨道。
（1）小球从最低点到最高点：可视为小球与圆弧轨道发生完全非弹性碰撞，用折合质
量法求小球上升的最大高度。列方程。
（2）小球从最低点到最高点再回到最低点：可视为小球与
圆弧轨道发生弹性碰撞，用速度增量法求解小球回到最低点
时的速度。
27.（2023四川成都三模）如图所示，一异形轨道由粗糙的水平部分和光滑的四分之一
圆弧部分组成，置于光滑的水平面上，如果轨道固定，将可视为质点的物块从圆弧轨道
的最高点由静止释放，物块恰好停在水平轨道的最左端。如果轨道不固定，仍将物块从
圆弧轨道的最高点由静止释放，下列说法正确的是( )
B
A.物块与轨道组成的系统机械能不守恒，动量守恒
B.物块与轨道组成的系统机械能不守恒，动量不守恒
C.物块运动不到水平轨道的最左端
D.物块将从轨道左端冲出水平轨道
【解析】 轨道不固定时，物块在轨道的水平部分运动时因摩擦产生热量，所
以系统的机械能不守恒；物块在轨道的圆弧部分下滑时，系统所受合外力不为零，动量
不守恒，但是水平方向动量守恒。
设轨道的水平部分长为，轨道固定时，根据能量守恒定律得 。
轨道不固定时，设物块与轨道相对静止时的共同速度为 ，在轨道水平部分滑行的距离
为，取水平向左为正方向，水平方向根据动量守恒定律得，可得 ，
根据能量守恒定律得，联立解得 ，所以物块仍能停在
水平轨道的最左端。
28.［多选］（2024云南师大附中模拟）如图所示，质量为的物块 静止在光滑水平
地面上，物块左侧面为圆弧面且与水平地面平滑连接，质量为的滑块以初速度
向右运动滑上，沿左侧面上滑一段距离后又返回，最后滑离 ，不计一切摩擦，滑块
从滑上到滑离的过程中，下列说法正确的是（重力加速度为 ）( )
BD
A.、 组成的系统动量守恒
B.合外力对的冲量大小为
C.对做的功为
D.沿上滑的最大高度为
【解析】 、 组成的系统在竖直方向所受合外力不为零，因此系统动量不守恒。
系统在水平方向所受合外力为零，在水平方向动量守恒，对整个过程，以向右为
正方向，由动量守恒定律得 ，由机械能守恒定律可得
，解得，对 由动量定理可得
（【点拨】运用大招将整个过程等效为弹性碰撞，可用速度
增量法求的速度。），合外力对的冲量大小为 。
对由动能定理得 。
沿 上滑到最大高度时，两者速度相等，在水平方向上，由动量守恒定律可得
. .
.
. .
. .
，由机械能守恒定律可得 （【点拨】将
沿 上升到最大高度的过程等效为完全非弹性碰撞过程，运用折合质量法求最大高度，
即列。），解得 。
. .
考点7 力学三大观点的综合应用
29.（2025云南昆明一中二次联考）一游戏
装置竖直截面如图所示，固定的光滑水平直
轨道、半径为的光滑螺旋圆形轨道 、
光滑水平直轨道 平滑连接，直轨道的左
边平滑连接一光滑曲面轨道。长为、质量为 的平板紧靠光滑且足够长的固定凹槽
左侧放置，平板上表面与齐平。将一质量为的小滑块从光滑曲面轨道 高
度处由静止释放，经过轨道后滑上平板并带动平板一起运动，平板到达 即被锁
定。已知，，，平板与滑块间的动摩擦因数 ，
滑块视为质点，最大静摩擦力等于滑动摩擦力，不计空气阻力，重力加速度 取
。
（1） 若滑块恰好能通过圆形轨道最高点点，求释放点的高度 ；
【答案】
【解析】 滑块恰好能通过圆形轨道最高点点时有
从滑块由高度处释放到运动至点过程，根据动能定理有
解得 。
（2） 滑块恰好过 点后，求平板加速至与滑块共速的过程中系统损耗的机械能；
【答案】
【解析】 滑块由高度处释放到运动至点，根据机械能守恒定律有
平板加速至与滑块共速过程，根据动量守恒定律有
根据能量守恒定律有
联立解得 。
（3） 要使滑块能到达 点，求释放点的高度范围。
【答案】
【解析】 ①设滑块以最小速度 滑上平板，对滑块、平板根据动量守恒定律有
系统能量守恒，有
当平板到达 锁定后，滑块继续向右减速（【抓题眼】此处的临界情况是平板锁定后，
滑块继续向右减速且到达 点时速度恰好减为0。）
有
从释放到运动至点，滑块机械能守恒，有
联立解得
②设滑块以最大速度 滑上平板，当滑到平板最右端时刚好共速，系统动量守恒，有
系统能量守恒，有
. .
从释放到运动至点，滑块机械能守恒，有
联立解得
故释放点的高度范围为 。
30.（2024安徽卷）如图所示，一实验小车静止在光
滑水平面上，其上表面有粗糙水平轨道与光滑四分之
一圆弧轨道。圆弧轨道与水平轨道相切于圆弧轨道最
低点，一物块静止于小车最左端，一小球用不可伸长
的轻质细线悬挂于 点正下方，并轻靠在物块左侧。
现将细线拉直到水平位置时，静止释放小球，小球运动到最低点时与物块发生弹性碰撞。
碰撞后，物块沿着小车上的轨道运动。已知细线长，小球质量 ，
物块、小车质量均为，小车上的水平轨道长 ，圆弧轨道半径
。小球、物块均可视为质点，不计空气阻力，重力加速度取 。
（1） 求小球运动到最低点与物块碰撞前瞬间所受拉力的大小；
【答案】
【解析】 小球运动到最低点的过程中，由动能定理有
解得
在最低点，对小球由牛顿第二定律有
解得小球运动到最低点与物块碰撞前瞬间所受拉力的大小为 。
（2） 求小球与物块碰撞后的瞬间，物块速度的大小；
【答案】
【解析】 小球与物块碰撞过程中，由动量守恒定律和机械能守恒定律有
解得小球与物块碰撞后的瞬间物块速度的大小为
。
（3） 为使物块能进入圆弧轨道，且在上升阶段不脱离小车，求物块与水平轨道间的动
摩擦因数 的取值范围。
【答案】
【解析】 若物块恰好运动到圆弧轨道的最低点时两者共速（【点拨】物块在圆弧轨道
底端和顶端与小车共速是两个临界情况，物块在圆弧轨道顶端时竖直方向速度恰好为
0。）
则物块与小车整体在水平方向动量守恒，有
由能量守恒定律有
解得
若物块恰好运动到与圆弧圆心等高的位置时两者共速
则物块与小车整体在水平方向动量守恒，有
由能量守恒定律有
解得
综上所述，物块与水平轨道间的动摩擦因数 的取值范围为 。
31.（2025河北部分学校调研）如图，为半径足够大的 光滑圆弧轨道，圆弧轨道末端
与右侧光滑水平面平滑连接，水平面 右侧平滑对接一足够长的水平传送带，传送
带正在以的速度逆时针匀速转动。有一质量为的物块 静止于圆
弧轨道底端，在物块右侧有一质量为的物块，物块 与传送带之间的动摩
擦因数，物块以水平向右、大小为 的速度从传送带左侧滑上传送
带。当物块滑离传送带后与物块发生碰撞，物块上有特殊装置，可以使物块、
碰撞瞬间让两者合在一起成为一个整体沿圆弧轨道向上运动，当、 整体沿圆弧轨道
向下运动到轨道底端时，该装置使物块、分开，物块停在轨道底端，物块 以分开
前瞬间的速度向右运动，之后物块、会多次作用，重力加速度大小
，不计空气阻力，两物块均可看作质点。求：
（1） 物块、第一次沿圆弧轨道向下运动到轨道底端分开时物块的速度大小 ；
【答案】
【解析】 传送带足够长，则物块 在传送带上向右滑动的速度一定能减小到0，传送带
的速度，小于物块初始的速度，则物块 第一次滑离传送带时
速度等于传送带的速度；设物块、第一次碰撞之后速度为，物块、
碰撞过程，根据动量守恒定律有
解得
物块、碰撞之后，沿圆弧轨道向上运动和返回过程中系统的机械能守恒，即、 分
开前瞬间它们的速度与第一次碰撞后的速度大小相等，所以、分开时物块 的速度为
。
（2） 物块从第一次滑上传送带到滑离传送带过程中摩擦产生的热量 ；
【答案】
【解析】 物块在传送带上向右减速运动过程根据牛顿第二定律有
解得
物块减速到0的时间
物块和传送带运动的位移分别为和 ，减速过程中相对滑动的位移为
物块在传送带上向左加速运动的加速度仍为
物块向左加速到与传送带速度相等时不再发生相对滑动，加速过程时间
设加速过程物块和传送带运动的位移分别为和 ，加速过程中相对滑动的位移为
整个过程产生的热量为 。
（3） 物块开始滑上传送带之后的整个过程中传送带对物块摩擦力的冲量 。
【答案】
【解析】 物块、第一次碰撞后，物块以速度滑上传送带，物块 的速度
小于传送带的速度，则物块向右减速到0后再向左加速，减速和加速过程的加速度大小
相等，根据运动的对称性可知物块离开传送带时速度大小也为，物块 在
传送带上运动的时间为
设物块、第二次碰撞之后速度为，物块、 碰撞过程，根据动量守恒定律有
解得
物块以速度滑上传送带，物块 的速度小于传送带的速度，则物块向右减
速到0后再向左加速，减速和加速过程的加速度大小相等，根据运动的对称性可知物块
离开传送带时速度大小也为；物块 在传送带上运动的时间为
之后重复上述过程，设物块、第次碰撞之后速度为，物块、 碰撞过程，根据
动量守恒定律有
解得
物块以速度滑上传送带，物块 的速度小于传送带的速度，
则物块向右减速到0后再向左加速，减速和加速过程的加速度大小相等，根据运动的对
称性可知物块离开传送带时速度大小也为；物块 在传送带
上运动的时间为
物块在传送带上与传送带相对滑动过程中物块 会受到水平向左的滑动摩擦力，速度
与传送带速度相等之后不再受到摩擦力的作用，则摩擦力的作用时间为
根据等比数列求和得
则摩擦力的冲量为 。
觉醒集训
1.（2024广东中山模拟）图是《天工开物》中记载的一种舂 米装置，
古人用脚踏一种像跷跷板一样的东西，将质量约为的碓抬高 后
从静止释放，碓在重力作用下向下运动，碓与谷物作用 后静止，每次碓
对谷物的平均作用力约为（重力加速度取 ）( )
B
A. B. C. D.
【解析】 碓在重力作用下向下运动，由动能定理可得 ，碓与谷物作
用过程，由动量定理可得 ，解得每次碓对谷物的平均作用力
。
2.（2024青海二模）斜向上发射的炮弹在最高点爆炸（爆炸时间
极短）成质量均为 的两块碎片，其中一块碎片沿原路返回。已
D
A. B. C. D.
【解析】 炮弹炸裂的过程水平方向动量守恒，设炮弹炸裂前的速度大小为 ，则
，得，设炸裂后瞬间另一块碎片的速度大小为 ，有
（【抓题眼】由题目条件“其中一块碎片沿原路返回”可知该碎片的
初速度与炮弹炸裂前的速度等大、反向。），解得 ，根据平抛运动规律有
，得，两块碎片落地点之间的距离 。
知炮弹爆炸时距地面的高度为，炮弹爆炸前的动能为，重力加速度大小为 ，不计空
气阻力和火药的质量，则两块碎片落地点间的距离为( )
. .
3.（2024江西上饶模拟预测）“双星”是宇宙中普遍存在的一种天体
系统，由两颗恒星组成，双星系统远离其他恒星，在相互的万有
引力作用下绕连线上一点做周期相同的匀速圆周运动。如图所
示，、两颗恒星构成双星系统，绕共同的圆心 做匀速圆周运
动，经过（小于周期）时间，、 两恒星的动量变化量分别为
、 ，则下列判断正确的是( )
D
A. B. C. D.
【解析】 系统所受的合外力为零，系统的总动量守恒，根据牛顿第二定律有
，加速度为，则有 。由于角速度相
同，因此，两恒星的速度方向始终相反，则 ，因此系统的总动
量始终为零，可得， 。
4.（2024山东菏泽三模）风筝在我国已存在两千年
之久，又有纸鸢、鹞子之称。如图所示，某时刻风
筝静止在空中，风筝面与水平面夹角为 ，牵引线
与竖直方向夹角为 。已知风筝质量为 ，垂直于
风筝面的风速大小为，风筝面的面积为 ，重力加
速度为 ，则风筝所在高度空气密度为( )
A
A. B. C. D.
【解析】 对风筝受力分析如图1所示，作出矢量三角形如图2所示，由几何关系可
知风筝此时获得的垂直于风筝面的力 ，根据牛顿第三定律，风筝对垂直
于风筝面的风的作用力大小也为，以风为研究对象，单位时间 内，垂直打在风筝面
的风的质量，在垂直于风筝面方向上由动量定理有 ，联立解得
空气密度为 。
5.（2025江西部分高中联盟校一模）如图，在水平地面上固定一
圆环，圆环内壁光滑，圆环内嵌着、 两个大小相同的小球，
它们的质量分别是、，且 ，小球的直径略小于圆
环的孔径，圆环的内半径远大于球的半径，初始时 球处于静止
状态，球以一定初速度撞击球，、两个球在 点发生弹性
碰撞，一段时间后，、两个球在 点发生第二次弹性碰撞，
、两点与圆环圆心的连线夹角为 ，则 为( )
A
A. B. C. D.
【解析】 两球发生弹性碰撞，设碰后速度分别为、 ，则根据动量守恒定律和
机械能守恒定律有， ，联立解得
，。第二次碰撞发生在题图中的 点，则从第一次碰撞到第
二次碰撞之间，有，，故 、
通过的路程之比为，则有 ，联立解得
，由于两质量均为正数，故，即 。
6.（2024山东菏泽模拟）如图甲所示，在光滑水平面上，小球以初动量 沿直线运动，
与静止的带轻质弹簧的小球发生正碰，此过程中，小球的动量随时间 变化的部分
图像如图乙所示，时刻图线的切线斜率最大，此时纵坐标为， 时刻纵坐标为零。
已知小球、 的直径相同，则( )
A.小球、的质量之比为
B. 时刻弹簧的弹性势能最大
C.小球的初动能和弹簧最大弹性势能之比为
D.时间内，小球的动量变化量为
C
【解析】 时刻图线的切线斜率最大，则小球的动量变化率最大，根据 ，
可知小球的速度变化率最大，即加速度最大，根据牛顿第二定律得 ，可知此时
弹簧弹力最大，由胡克定律可知，此时弹簧形变量最大，则此时弹簧的弹性势能最大。
时刻两小球共速，设速度大小均为，则小球的质量 ，根据动量守恒有
，则小球的质量 ，由此可知两小球的质量之比为
。
根据和机械能守恒定律有，小球 的初动能和弹簧
最大弹性势能之比 。
时间内，小球的动量变化量 。
7.（2024重庆沙坪坝区三模）如图所示，质量为的小物块放在质量也为 的
木板的右端，木板静止在光滑地面上，时刻给木板施加一水平向右的拉力 ，物
块和木板立即发生相对滑动。已知拉力功率恒为 ，物块和木板间的动摩擦因数
，时物块和木板共速，且共速时立即撤去拉力，重力加速度 取
。
（1） 求与木板共速前物块 运动的加速度；
【答案】 ，方向水平向右
【解析】 、共速之前，对进行分析，根据牛顿第二定律有
解得
A向右做匀加速直线运动，加速度方向水平向右。
（2） 若物块恰不从木板上滑下，求木板 的长度；
【答案】
【解析】 结合上述，、达到相等的速度时有
对、 组成的系统，根据能量守恒定律有
解得 。
（3） 若木板右方还静置着另一物块，木板与共速后再与 发生碰撞并粘在一起，
则在满足第（2）问情况下，要保证物块恰不从木板上滑出，求物块 的质量。
【答案】
【解析】 根据题意，、发生完全非弹性碰撞，则有
拉力撤去后到三者共速，对、、 组成的系统，根据动量守恒定律有
B、碰后到、、 三者共速过程，根据能量守恒定律有
结合上述解得 （另一解不合题意，舍去）。
8.（2024河北邯郸一模）如图所
示，桌面、地面和固定的螺旋
形圆管均光滑，轻质弹簧左端
固定，自然伸长位置为 点，弹
簧的劲度系数，圆轨道的半径，圆管的内径比小球 直径略
大，但远小于圆轨道半径，小物块静止于木板 左端，木板的上表面恰好与圆管轨
道水平部分下端表面等高，小物块与木板上表面间的动摩擦因数 ，木板右端与
墙壁之间的距离，现用力将小球向左推压，将弹簧压缩 ，然后由
静止释放小球，小球与弹簧不连接，小球运动到桌面右端点后水平抛出，从管口 处
沿圆管切线飞入圆管内部，从圆管水平部分点飞出，并恰好与小物块 发生弹性碰撞，
经过一段时间后和右侧墙壁发生弹性碰撞，已知 始终未和墙壁碰撞，并且未脱离
木板，，，取，， ，
。求：
（1） 小球平抛运动的时间及抛出点与管口间的高度差 ；
【答案】 ;
【解析】 弹簧弹开小球过程弹力随位移均匀变化，由动能定理可得
在小球平抛到管口点时如图，根据 ，
（【点拨】“从管口处沿圆管切线飞入圆管内部”说明小球在 点
的速度方向沿圆管过点的切线方向斜向下。），
联立解得， 。
. .
（2） 小球在圆管内运动过程中对圆管最高点的挤压力 ，并判断是和管的内壁还是
外壁挤压；
【答案】 ，方向竖直向上; 和外壁挤压
【解析】 从 到圆管最高点的过程，由动能定理可得
由上述图可知
在最高点有
解得圆管对小球的支持力 ，方向竖直向下
根据牛顿第三定律可知，小球对圆管的挤压力 ，方向竖直向上
说明小球和圆筒外壁挤压。
（3） 木板的最短长度及木板在地面上滑动的总路程 。
【答案】 ;
【解析】 从到 全过程，由动能定理可得
解得
小球和物块碰撞过程，取水平向右为正方向，可得 ，
解得，（【点拨】小球与小物块质量相等， ，且两者发生
的为弹性碰撞，碰后速度交换。）
说明碰后小球停止运动，物块获得且水平向右的速度，开始在木板上滑动，以
和为对象，可得
对可得
解得，
则物块与木板共速后与墙壁发生碰撞，以和 为对象，第1次与墙碰撞后
解得
对木板有，
. .
第2次与墙碰撞后
解得
对木板有
第3次与墙碰撞后
解得
对木板有
……
第次与墙碰撞后
解得
对木板有
第次与墙碰撞后
解得
对木板有
木板运动的总路程为
即当 时，，可得
代入数据解得
木板和物块最终停在右侧墙壁处，物块恰好停在右端，根据能量守恒可得
解得 。
觉醒原创
1.如图所示，神舟十六号航天员朱杨柱、桂海潮在中国空间站太空舱内面向全国青少年
进行太空科普授课。朱杨柱先将一个钢球放在标准网格布的前方，随后桂海潮将一个质
量和形状都相同的钢球与朱杨柱放的钢球完成对心碰撞。下列关于这个过程的说法正确
的是( )
A
A.朱杨柱放钢球后，钢球将绕地球做圆周运动
B.两个钢球在太空中碰撞，动量守恒定律不适用
C.朱杨柱在太空舱内拿着钢球静止时，钢球动量不变
D.碰撞前后两个钢球的动量变化相同
【解析】 由于在太空舱内，小球处于完全失重状态，在太空舱外观察，太空舱和
小球均绕地球做圆周运动，万有引力全部提供向心力。
动量守恒定律适用条件并不由钢球是否完全失重来决定，故仍然适用。
朱杨柱在太空舱拿着钢球静止时，钢球绕地球做圆周运动，因此钢球动量的方向
变化。
由动量定理可知，碰撞前后两个钢球动量变化大小相同，方向相反。
2.［多选］一质量为的小球，以初速度 冲上一个质量为
、半径为的圆弧形凹槽。 为凹槽的圆心，凹槽所对的圆
心角为 ，凹槽不固定。所有接触面均光滑，
重力加速度为， ，下列说法正确的是( )
CD
A.无论 为多大，小球只要能冲出凹槽，在 点的水平方向分速度就一定等于凹槽的速度
B.只有 且小球能冲出凹槽时，小球在 点的水平方向分速度才等于凹槽的速度
C.当，且 时，小球运动的最大离地高度为
D.若 ，且小球从 点离开时小球相对凹槽的速度大小等于凹槽的对地速度，则
此时凹槽的速度大小为
【解析】 由相对运动可知 小球相对凹槽的速度 ，即
图1
可知当 不为 且小球能冲出凹槽时，小
球水平方向的分速度大于凹槽的速度，此时速
度关系如图1所示，只有当 时，只要小
球可以运动到点，小球在 点的水平方向分速
度等于凹槽的速度；当 小于 且小球刚好
能运动到点时，小球在 点的水平方向分速度
也等于凹槽的速度。
假设小球能从 点冲出凹槽，由系统能量守恒，水平方向动量守恒，小球运动到距
离地面最高点过程有， ，解得小球运动
. .
的最大离地高度 (【点拨】用折合质量法快速计算小球的重力势能
代入数据解得 )
又因为，则，则 ，假设成立。
图2
由图1可知，当 时，小球从 点离开时相对凹槽的
速度与水平方向夹角为 ，此时小球相对凹槽的速度大小等
于凹槽的对地速度，作出小球的速度、凹槽的速度、小球相对
凹槽的速度的矢量三角形，如图2。故此时小球速度与凹槽速度
夹角为 ，由几何关系可知小球的速度 ，有水平
方向动量守恒可得，解得 。
. .