考向三 带电粒子在拼接场中的运动-2025年高考物理专题复习课件
文档属性
| 名称 | 考向三 带电粒子在拼接场中的运动-2025年高考物理专题复习课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-02-18 09:45:54 | ||
图片预览








文档简介
(共27张PPT)
专题十 磁场
考向三 带电粒子在拼接场中的运动
2025年高考物理专题复习资料
考点切片
考点1 带电粒子在拼接场中运动的科技应用
1.(2023广东卷)某小型医用回旋加速器,最大回旋半径为 ,磁感应强度大小为
,质子加速后获得的最大动能为 。根据给出的数据,可计算质子经该
回旋加速器加速后的最大速率约为(忽略相对论效应, )( )
C
A. B. C. D.
【解析】 由洛伦兹力提供向心力有 ,质子加速后获得的最大动能为
,代入数据,联立解得最大速率 。
2.(2024重庆八中月考)如图甲所示为质谱仪工作的原理图,已知质量为 、电荷量为
的粒子,从容器下方的小孔飘入电势差为 的加速电场,其初速度几乎为0,经电场
加速后,由小孔沿着与磁场垂直的方向进入磁感应强度为的匀强磁场中。粒子在 点
的速度与磁场边界垂直,最后打在照相底片上的点,且 。忽略粒子的重力,通
过测量得到与的关系如图乙所示,已知斜率为 ,匀强磁场的磁感应
强度, 取 ,则下列说法正确的是( )
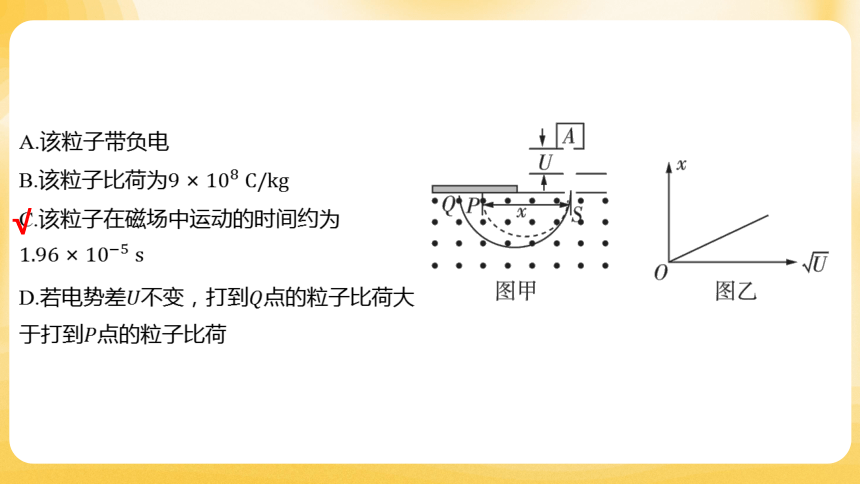
A.该粒子带负电
B.该粒子比荷为
C.该粒子在磁场中运动的时间约为
D.若电势差不变,打到 点的粒子比荷大
于打到 点的粒子比荷
√
【解析】 粒子进入磁场后向左偏转,根据左手定则可知,该粒子带正电。
粒子经过加速电场的过程,根据动能定理可得,解得 ,粒子在磁场
中由洛伦兹力提供向心力可得,可得 ,则有
,已知图像的斜率为 (【点拨】对于题
图乙这种图像,只给出横、纵坐标轴表示的物理量和一条倾斜的图线,从图像中只能判断
出图线过原点,斜率为定值,则需要我们求出该图像所对应的函数方程,并表示出斜率。),
可得粒子的比荷为 。
. .
. .
该粒子在磁场中运动的时间为 。
根据可知,若电势差不变,则打到点的粒子比荷小于打到 点
的粒子比荷。
3.[多选](2024内蒙古呼伦贝尔模拟)回旋加速器的工作原理如图所示,D形金属盒
的半径为,两D形盒间狭缝的宽度为,匀强磁场的磁感应强度大小为 、方向与盒面
垂直。D形金属盒的中心处有一粒子源,能产生质量为、电荷量为 的质子
(的初速度及其所受重力均不计),质子在加速电压为 的电场中加速,最终从出口
处射出。下列说法正确的是( )
AC
A.质子在电场中运动的总时间为
B.质子在磁场中运动的总时间为
C.若仅将电压 增大,则质子从出口处射出的最大动能不变
D.若仅将处的粒子源改为氦 核源,则氦核可获得的最
大动能为
【解析】 当质子射出D形盒时,根据洛伦兹力提供向心力可得,则 ,
质子在电场中的加速度大小为,质子在电场中运动的总时间 。
设在电场中加速度的次数为,根据动能定理 ,在电场中加速一次后,在磁
场中运动半圈,在磁场中运动半圈的时间 ,质子在磁场中运动的总时间
。
当质子射出D形盒时,质子的速度,若仅将电压 增大,则质子从出口处射出的
最大速度不变,最大动能不变。
若仅将处的粒子源改为氦 核源,则与质子比较,电荷量增大为2倍,质量增大为
4倍,则氦核可获得的最大速度为,最大动能 。
考点2 带电粒子在拼接场中的运动
大招61 对应练习
解题觉醒
1.题型特征:带电粒子以垂直于电场线方向的初速度先进入匀强电场,再进入匀强磁场。
2.解题技巧
(1)求
(2)求速弦角
(3)求进入磁场时的速度 。
4.(2024贵州安顺模拟)如图,在平面直角坐标系 的
第一、四象限存在方向沿 轴正方向的匀强电场,在第二、
三象限的区域存在方向垂直于 平面向外的匀强磁场,
磁感应强度大小为。一个带负电的粒子(重力不计)从
轴上的点以大小为的初速度沿 轴正方向射出,粒子在
电场和磁场中运动后回到点。则场强 的大小为( )
B
A. B. C. D.
【解析】 依题意,粒子的运动轨迹如图,粒子从轴进入磁场时速度方向与轴夹角为 ,
则进入磁场时的速度,沿轴方向的速度,其中 ,粒子在
磁场中运动的半径,联立解得 ,故选B。
5.(2024广东卷)如图甲所示,两块平行正对的金属板水
平放置,板间加上如图乙所示幅值为、周期为 的交变
电压。金属板左侧存在一水平向右的恒定匀强电场,右侧
分布着垂直纸面向外的匀强磁场。磁感应强度大小为 。
一带电粒子在 时刻从左侧电场某处由静止释放,在
时刻从下板左端边缘位置水平向右进入金属板间的
电场内,在 时刻第一次离开金属板间的电场、水平
向右进入磁场,并在 时刻从下板右端边缘位置再次
水平进入金属板间的电场。已知金属板的板长是板间距离的倍,粒子质量为 。忽略
粒子所受的重力和场的边缘效应。
(1) 判断带电粒子的电性并求其所带的电荷量 ;
【答案】 正电;
【解析】 根据带电粒子在右侧磁场中的运动轨迹结合左手定则可知,粒子带正电;粒子
在磁场中运动的周期为
根据
则粒子所带的电荷量 。
(2) 求金属板的板间距离和带电粒子在时刻的速度大小 ;
【答案】 ;
【解析】 若金属板的板间距离为,则板长为,粒子在板间运动时,
出电场时竖直方向的速度为零,则竖直方向
在磁场中时
其中的
联立解得, 。
(3) 求从 时刻开始到带电粒子最终碰到上金属板的过程中,电场力对粒子做的
功 。
【答案】
【解析】 带电粒子在电场和磁场中的运动轨迹如图,
由(2)的计算可知金属板的板间距离
则粒子在时刻再次进入中间的偏转电场,在 时刻进入左侧的电场做减速运动速度为
零后反向加速,在时刻再次进入中间的偏转电场, 时刻碰到上极板,因粒子在偏转
电场中运动时,在时间 内电场力做功为零,在左侧电场中运动时,往返一次电场力做功也
为零,可知整个过程中只有开始进入左侧加速电场时电场力做功和最后 时间内电场
力做功(【点拨】静电场中电场力做功只与粒子初、末位置的电势差有关,与路径无
关。),则 。
. .
. .
【抓题眼】由题述粒子进入电场和磁场的时间及题图乙可知, 时间内粒子做类
平抛运动,时间内粒子做逆向类平抛运动, 时间内粒子做匀速圆周运
动(半个圆周)。
6.(2023山东卷)如图所示,在, 的区域
中,存在沿轴正方向、场强大小为 的匀强电场,电场的周
围分布着垂直纸面向外的恒定匀强磁场。一个质量为 、电荷
量为的带正电粒子从中点 进入电场(不计粒子重力)。
(1) 若粒子初速度为零,粒子从上边界垂直 第二次离开
电场后,垂直再次进入电场,求磁场的磁感应强度 的大小;
【答案】
图1
【解析】 根据题意作出粒子的运动轨迹,如图1所示,设粒子经
电场加速后进入磁场的速度大小为 ,在磁场中做匀速圆周运动
的半径为 ,则由动能定理得
由牛顿第二定律得
由几何关系得
联立解得 。
(2) 若改变电场强度大小,粒子以一定的初速度从点沿 轴正方向第一次进入电场,
离开电场后从点第二次进入电场,在电场的作用下从 点离开。
(ⅰ) 求改变后电场强度的大小和粒子的初速度 ;
【答案】 36; ,沿 轴正方向
图2
【解析】 带电粒子运动轨迹如图2所示,设粒子第一次经电场
加速后进入磁场的速度大小为 ,在磁场中做匀速圆周运动的
半径为,粒子从点第二次进入电场时速度的方向与 轴负方
向的夹角为 ,第二次在电场中运动的时间为 ,则在电场中由动
能定理得
由牛顿第二定律得
由几何关系得
解得
、
粒子从 点第二次进入电场后,在电场中运动时,由运动学公式得
联立解得
,沿 轴正方向。
(ⅱ) 通过计算判断粒子能否从 点第三次进入电场。
【答案】 不能
【解析】 解法一:设粒子从点离开电场时,速度大小为,方向与轴正方向的夹角为 ,
沿轴方向的分量为,在磁场中做匀速圆周运动的半径为 ,则由运动学公式得
由牛顿第二定律得
解得
假设粒子能从点第三次进入电场,对应的轨迹半径为 ,如图3所示,由几何关系得
图3
解得
由于,故假设不成立,即粒子不能从 点第三次进入电场。
解法二:如图3所示,设粒子从点离开电场时,速度大小为,方向与轴正方向的夹角为 ,
在磁场中做匀速圆周运动的半径为,圆心(图中未画出)位置坐标为 ,由几何关系有
,
粒子在电场中运动,由动能定理有
由几何关系得
粒子在磁场中运动,由牛顿第二定律得
联立解得、、
则点到圆心的距离
因为,所以粒子不能从 点第三次进入电场。
专题十 磁场
考向三 带电粒子在拼接场中的运动
2025年高考物理专题复习资料
考点切片
考点1 带电粒子在拼接场中运动的科技应用
1.(2023广东卷)某小型医用回旋加速器,最大回旋半径为 ,磁感应强度大小为
,质子加速后获得的最大动能为 。根据给出的数据,可计算质子经该
回旋加速器加速后的最大速率约为(忽略相对论效应, )( )
C
A. B. C. D.
【解析】 由洛伦兹力提供向心力有 ,质子加速后获得的最大动能为
,代入数据,联立解得最大速率 。
2.(2024重庆八中月考)如图甲所示为质谱仪工作的原理图,已知质量为 、电荷量为
的粒子,从容器下方的小孔飘入电势差为 的加速电场,其初速度几乎为0,经电场
加速后,由小孔沿着与磁场垂直的方向进入磁感应强度为的匀强磁场中。粒子在 点
的速度与磁场边界垂直,最后打在照相底片上的点,且 。忽略粒子的重力,通
过测量得到与的关系如图乙所示,已知斜率为 ,匀强磁场的磁感应
强度, 取 ,则下列说法正确的是( )
A.该粒子带负电
B.该粒子比荷为
C.该粒子在磁场中运动的时间约为
D.若电势差不变,打到 点的粒子比荷大
于打到 点的粒子比荷
√
【解析】 粒子进入磁场后向左偏转,根据左手定则可知,该粒子带正电。
粒子经过加速电场的过程,根据动能定理可得,解得 ,粒子在磁场
中由洛伦兹力提供向心力可得,可得 ,则有
,已知图像的斜率为 (【点拨】对于题
图乙这种图像,只给出横、纵坐标轴表示的物理量和一条倾斜的图线,从图像中只能判断
出图线过原点,斜率为定值,则需要我们求出该图像所对应的函数方程,并表示出斜率。),
可得粒子的比荷为 。
. .
. .
该粒子在磁场中运动的时间为 。
根据可知,若电势差不变,则打到点的粒子比荷小于打到 点
的粒子比荷。
3.[多选](2024内蒙古呼伦贝尔模拟)回旋加速器的工作原理如图所示,D形金属盒
的半径为,两D形盒间狭缝的宽度为,匀强磁场的磁感应强度大小为 、方向与盒面
垂直。D形金属盒的中心处有一粒子源,能产生质量为、电荷量为 的质子
(的初速度及其所受重力均不计),质子在加速电压为 的电场中加速,最终从出口
处射出。下列说法正确的是( )
AC
A.质子在电场中运动的总时间为
B.质子在磁场中运动的总时间为
C.若仅将电压 增大,则质子从出口处射出的最大动能不变
D.若仅将处的粒子源改为氦 核源,则氦核可获得的最
大动能为
【解析】 当质子射出D形盒时,根据洛伦兹力提供向心力可得,则 ,
质子在电场中的加速度大小为,质子在电场中运动的总时间 。
设在电场中加速度的次数为,根据动能定理 ,在电场中加速一次后,在磁
场中运动半圈,在磁场中运动半圈的时间 ,质子在磁场中运动的总时间
。
当质子射出D形盒时,质子的速度,若仅将电压 增大,则质子从出口处射出的
最大速度不变,最大动能不变。
若仅将处的粒子源改为氦 核源,则与质子比较,电荷量增大为2倍,质量增大为
4倍,则氦核可获得的最大速度为,最大动能 。
考点2 带电粒子在拼接场中的运动
大招61 对应练习
解题觉醒
1.题型特征:带电粒子以垂直于电场线方向的初速度先进入匀强电场,再进入匀强磁场。
2.解题技巧
(1)求
(2)求速弦角
(3)求进入磁场时的速度 。
4.(2024贵州安顺模拟)如图,在平面直角坐标系 的
第一、四象限存在方向沿 轴正方向的匀强电场,在第二、
三象限的区域存在方向垂直于 平面向外的匀强磁场,
磁感应强度大小为。一个带负电的粒子(重力不计)从
轴上的点以大小为的初速度沿 轴正方向射出,粒子在
电场和磁场中运动后回到点。则场强 的大小为( )
B
A. B. C. D.
【解析】 依题意,粒子的运动轨迹如图,粒子从轴进入磁场时速度方向与轴夹角为 ,
则进入磁场时的速度,沿轴方向的速度,其中 ,粒子在
磁场中运动的半径,联立解得 ,故选B。
5.(2024广东卷)如图甲所示,两块平行正对的金属板水
平放置,板间加上如图乙所示幅值为、周期为 的交变
电压。金属板左侧存在一水平向右的恒定匀强电场,右侧
分布着垂直纸面向外的匀强磁场。磁感应强度大小为 。
一带电粒子在 时刻从左侧电场某处由静止释放,在
时刻从下板左端边缘位置水平向右进入金属板间的
电场内,在 时刻第一次离开金属板间的电场、水平
向右进入磁场,并在 时刻从下板右端边缘位置再次
水平进入金属板间的电场。已知金属板的板长是板间距离的倍,粒子质量为 。忽略
粒子所受的重力和场的边缘效应。
(1) 判断带电粒子的电性并求其所带的电荷量 ;
【答案】 正电;
【解析】 根据带电粒子在右侧磁场中的运动轨迹结合左手定则可知,粒子带正电;粒子
在磁场中运动的周期为
根据
则粒子所带的电荷量 。
(2) 求金属板的板间距离和带电粒子在时刻的速度大小 ;
【答案】 ;
【解析】 若金属板的板间距离为,则板长为,粒子在板间运动时,
出电场时竖直方向的速度为零,则竖直方向
在磁场中时
其中的
联立解得, 。
(3) 求从 时刻开始到带电粒子最终碰到上金属板的过程中,电场力对粒子做的
功 。
【答案】
【解析】 带电粒子在电场和磁场中的运动轨迹如图,
由(2)的计算可知金属板的板间距离
则粒子在时刻再次进入中间的偏转电场,在 时刻进入左侧的电场做减速运动速度为
零后反向加速,在时刻再次进入中间的偏转电场, 时刻碰到上极板,因粒子在偏转
电场中运动时,在时间 内电场力做功为零,在左侧电场中运动时,往返一次电场力做功也
为零,可知整个过程中只有开始进入左侧加速电场时电场力做功和最后 时间内电场
力做功(【点拨】静电场中电场力做功只与粒子初、末位置的电势差有关,与路径无
关。),则 。
. .
. .
【抓题眼】由题述粒子进入电场和磁场的时间及题图乙可知, 时间内粒子做类
平抛运动,时间内粒子做逆向类平抛运动, 时间内粒子做匀速圆周运
动(半个圆周)。
6.(2023山东卷)如图所示,在, 的区域
中,存在沿轴正方向、场强大小为 的匀强电场,电场的周
围分布着垂直纸面向外的恒定匀强磁场。一个质量为 、电荷
量为的带正电粒子从中点 进入电场(不计粒子重力)。
(1) 若粒子初速度为零,粒子从上边界垂直 第二次离开
电场后,垂直再次进入电场,求磁场的磁感应强度 的大小;
【答案】
图1
【解析】 根据题意作出粒子的运动轨迹,如图1所示,设粒子经
电场加速后进入磁场的速度大小为 ,在磁场中做匀速圆周运动
的半径为 ,则由动能定理得
由牛顿第二定律得
由几何关系得
联立解得 。
(2) 若改变电场强度大小,粒子以一定的初速度从点沿 轴正方向第一次进入电场,
离开电场后从点第二次进入电场,在电场的作用下从 点离开。
(ⅰ) 求改变后电场强度的大小和粒子的初速度 ;
【答案】 36; ,沿 轴正方向
图2
【解析】 带电粒子运动轨迹如图2所示,设粒子第一次经电场
加速后进入磁场的速度大小为 ,在磁场中做匀速圆周运动的
半径为,粒子从点第二次进入电场时速度的方向与 轴负方
向的夹角为 ,第二次在电场中运动的时间为 ,则在电场中由动
能定理得
由牛顿第二定律得
由几何关系得
解得
、
粒子从 点第二次进入电场后,在电场中运动时,由运动学公式得
联立解得
,沿 轴正方向。
(ⅱ) 通过计算判断粒子能否从 点第三次进入电场。
【答案】 不能
【解析】 解法一:设粒子从点离开电场时,速度大小为,方向与轴正方向的夹角为 ,
沿轴方向的分量为,在磁场中做匀速圆周运动的半径为 ,则由运动学公式得
由牛顿第二定律得
解得
假设粒子能从点第三次进入电场,对应的轨迹半径为 ,如图3所示,由几何关系得
图3
解得
由于,故假设不成立,即粒子不能从 点第三次进入电场。
解法二:如图3所示,设粒子从点离开电场时,速度大小为,方向与轴正方向的夹角为 ,
在磁场中做匀速圆周运动的半径为,圆心(图中未画出)位置坐标为 ,由几何关系有
,
粒子在电场中运动,由动能定理有
由几何关系得
粒子在磁场中运动,由牛顿第二定律得
联立解得、、
则点到圆心的距离
因为,所以粒子不能从 点第三次进入电场。
同课章节目录
