考向一 光的折射和全反射
图片预览








文档简介
(共32张PPT)
专题十四 光学
考向一 光的折射和全反射
2025年高考物理专题复习资料
考点切片
考点1 光的折射和折射率
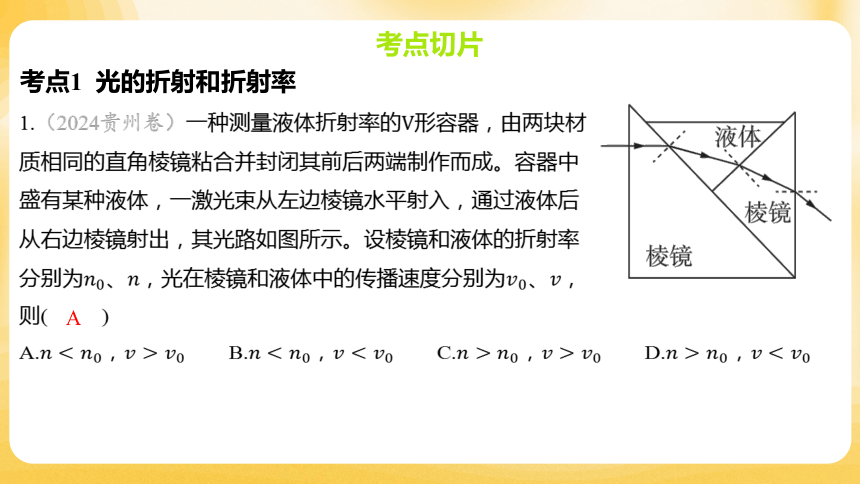
1.(2024贵州卷)一种测量液体折射率的 形容器,由两块材
质相同的直角棱镜粘合并封闭其前后两端制作而成。容器中
盛有某种液体,一激光束从左边棱镜水平射入,通过液体后
从右边棱镜射出,其光路如图所示。设棱镜和液体的折射率
分别为、,光在棱镜和液体中的传播速度分别为、 ,
则( )
A
A., B., C., D.,
【解析】 由题图可知光从棱镜进入液体中时,入射角小于折射角,根据折射定律可知
,由折射率与速度的关系式可得 ,故选A。
跳跳学长 敲黑板
定义式 (不论光从真空斜射入介质,还是从介质斜射入真空, 总是真
空中的光线与法线间的夹角, 总是介质中的光线与法线间的夹角。
影响因素 折射率由介质本身的性质决定,与入射角的大小无关。折射率还与光的
频率有关,同一种介质中,光的频率越大,介质对其折射率越大,光在该介
质中的传播速度越小。
与光速的关系 , 是光在该介质中的传播速度。
提醒 折射率与介质的密度没有关系,光密介质不是指密度大的介质。
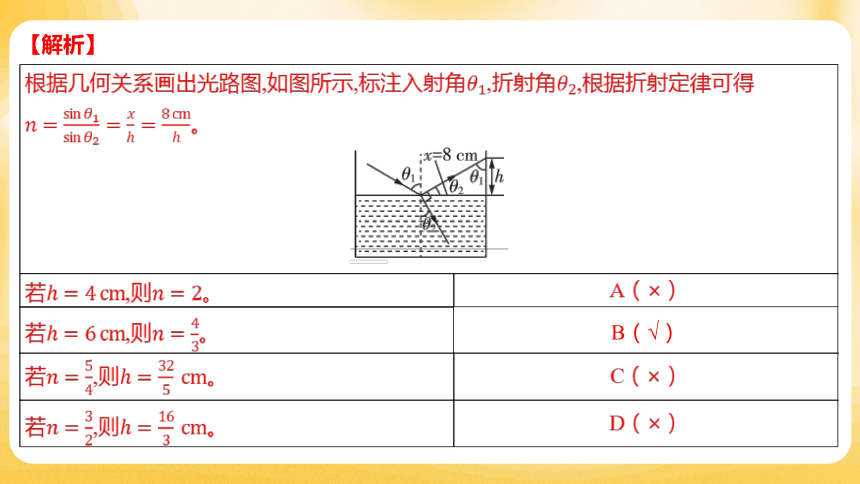
2.(2024重庆卷)某同学设计了一种测量液体折射率的方案。过
容器中心轴线的剖面图如图所示,其宽度为 ,让单色光在此
剖面内从空气入射到液体表面的中心。调整入射角,当反射光与
折射光垂直时,测出竖直器壁上的反射光点与液体表面的距离 ,
就能得到液体的折射率 。忽略器壁厚度,由该方案可知( )
B
A.若,则 B.若,则
C.若,则 D.若,则
【解析】
根据几何关系画出光路图,如图所示,标注入射角,折射角 ,根据折射定律可得 。 ________________________________________ 若,则 。 A( )
若,则 。 B(√)
若,则 。 C( )
若,则 。 D( )
3.[多选](2024湖南模拟预测)雨过天晴,
空气中悬浮着大量小水滴,若太阳光从背后
近乎水平入射,观察者便会看到彩虹,如图
甲所示。有时能够同时观察到两道彩虹,内
层彩虹被称为“虹”,外层彩虹被称为“霓”。
BC
A.“虹”对应光路图中1级光,色序表现为“内红外紫”
B.“霓”对应光路图中2级光,色序表现为“内红外紫”
C.对同一束入射日光,产生“虹”现象时红光在水滴内传播时间小于紫光
D.对同一束入射日光,产生“虹”现象时紫光在水滴内传播时间小于红光
这是由阳光在小水滴内部反射次数不同导致的。彩虹现象形成时,阳光在小水滴中的大
致光路如图乙所示。关于彩虹现象,下列说法正确的有( )
【解析】 由题可知,内层彩虹被称为“虹”,所以对应光路图
中1级光。根据紫光频率大于红光,可知紫光入射小水滴时折射率
较大,由此作出“虹”的光路图如图所示,色序表现为“内紫外红”。
“霓”的产生和“虹”类似,但日光在水滴中反射两次,对应光路
图中2级光,色序排列表现与“虹”相反,表现为“内红外紫”。
对同一束入射光,产生“虹”现象时,设折射角为 ,球形
水滴的半径为,有, ,光传播的路程为 ,则光在水滴中的传
播时间为
,红光和紫光有相同的入射角 ,而水
滴对紫光的折射率大于对红光的折射率,则紫光在水滴内的传播时间大于红光在水滴内
的传播时间。
考点2 光的全反射
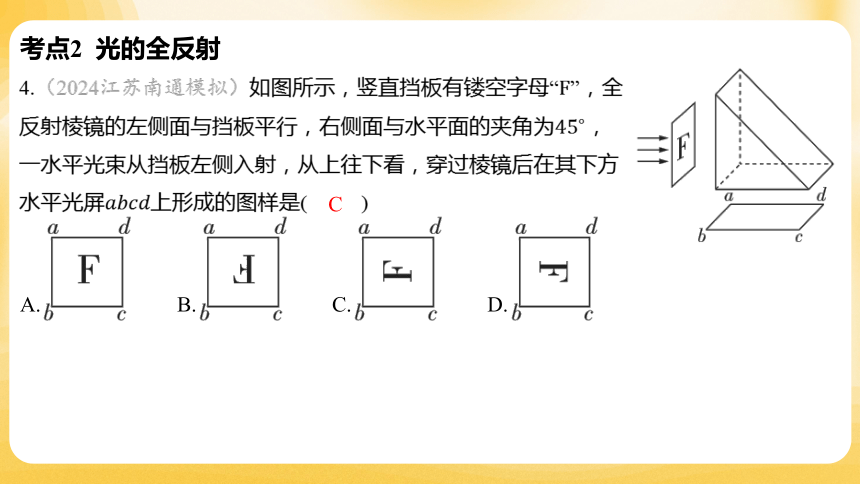
4.(2024江苏南通模拟)如图所示,竖直挡板有镂空字母“ ”,全
反射棱镜的左侧面与挡板平行,右侧面与水平面的夹角为 ,
一水平光束从挡板左侧入射,从上往下看,穿过棱镜后在其下方
水平光屏 上形成的图样是( )
C
A. B. C. D.
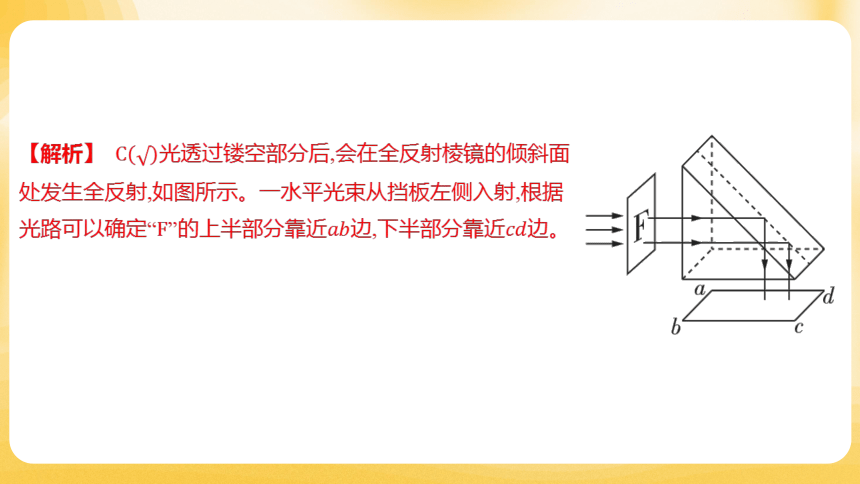
【解析】 光透过镂空部分后,会在全反射棱镜的倾斜面
处发生全反射,如图所示。一水平光束从挡板左侧入射,根据
光路可以确定“”的上半部分靠近边,下半部分靠近 边。
5.[多选](2025安徽名校联考)水底灯是水中环境常用的灯具之一,在夜间可以营造
出非常美丽的水下场景,增加水下的浪漫感和视觉效果。某公园水池底部安装了可视为
点光源的灯和 灯,两灯到水面的距离相等,如图所示。两灯发出不同颜色的光,分
别为光、光,从每盏灯的正上方观察,发现灯的视深大于 灯的视深,则下列说法
正确的是( )
AC
A.水对光的折射率比对 光的折射率要小
B.在水中,光的传播速度大于 光的传播速度
C.灯照亮水面的面积大于 灯照亮的面积
D.将光和光通过相同的双缝干涉装置, 光的干涉条纹间距
较大
图1
【解析】 设实际深度为,视深为 ,作出光路图如图1所示。
根据折射率定义式有,结合几何关系有 ,
由于从正上方观察,与很小,则有 ,
, 解得,故水对光的折射率比对 光的折射率要
小。
根据可知,在水中光的传播速度小于 光的传播速度。
图2
如图2所示,灯照亮水面的面积
,而,所以 灯照亮水面
的面积比 灯的大。
光的折射率较小,则频率较小,根据,可得 光的波
长较长,由 可知, 光的干涉条纹间距较大。
6.(2024浙江温州模拟)如图甲所示,有一玻璃砖侧面为直角三角形,角 为直角,
边上有一点光源,光源发出的光波长可调。光在玻璃砖上发生全反射的临界角为 ,
在边上有光射出的长度为,作出 图像,如图乙所示。若直线1的斜率为
,直线2在纵轴上的截距为,不考虑二次反射,则 的长度为( )
B
A. B. C. D.
【解析】 过向作垂线,长为,如图所示,利用几何关系可知 ,当临界角
大于时,下方出射的光线能到达点,关系满足 ,利用题
中已知斜率和截距,由①②两个方程得出,(【点拨】函数 对
应图线1,斜率,函数对应图线2,纵截距 。),
则,因此 ,故选B。
. .
考点3 光的折射和全反射的综合应用
大招72 对应练习
解题觉醒
1.题型特征:画光路图,利用几何分析,求长度、角度或折射率
2.规律总结
(1)起手先写“由几何关系”。
(2)如果已知折射率
(3)只要光从光密介质射入光疏介质,一定要验证是否有全反射。
(4)留意
(5)圆内很容易出现等腰三角形。
7.(2024全国甲卷)一玻璃柱的折射率,其横截面为四分之一圆,圆的半径为 ,
如图所示。截面所在平面内,一束与边平行的光线从圆弧入射。入射光线与 边的
距离由小变大,距离为时,光线进入柱体后射到边恰好发生全反射。求此时与
的比值。
【答案】
【解析】 根据题意可画出入射光线与边的距离为 时的光路图,如图所示
则由折射定律有
,
由全反射临界角公式有
。
由几何关系可得(【点拨】物理当中用到的一些简单几何关系时不需要具体说明什么样
的几何关系,直接写“由几何关系可得”,并写出结论即可。所以小伙伴们,要想学好物理,一
些数学知识是必不可少的。曾经还有人说过如果一个人可以称得上是物理学家,那他一
定也是一个数学家。)
,
,
联立解得 。
8.(2022湖南卷)如图所示,某种防窥屏由
透明介质和对光完全吸收的屏障构成,其中
屏障垂直于屏幕平行排列,可实现对像素单
元可视角度的控制(可视角度 定义为
某像素单元发出的光在图示平面内折射到空
(1) 若把发光像素单元视为点光源,要求可视角度控制为,求屏障的高度 ;
【答案】
气后最大折射角的2倍)。透明介质的折射率,屏障间隙 。发光像素单
元紧贴屏下,位于相邻两屏障的正中间,不考虑光的衍射。
(2) 若屏障高度,且发光像素单元的宽度不能忽略,求像素单元宽度 最
小为多少时,其可视角度刚好被扩为 (只要看到像素单元的任意一点,即视为
能看到该像素单元)。
【答案】
【解析】
1.构建模型 (1)长方体透明介质,可视角度为 时的光路图如图1所示——折射
角为 ;
___________________________________
图1
1.构建模型 (2)可视角度为 时的光路图如图2所示——折射角为
_______________________________________
图2
2.定角度 第(1)问入射角为,折射角为 ;
第(2)问入射角为,折射角为
3.根据折射定 律和几何关系 列方程 (1)由几何关系则,,解得 ,
;
(2)发光像素单元最左端与屏障的距离为 ,像素
单元宽度最小为
9.(2023山东卷)一种反射式光纤位移传感器可以实现微小位移测
量,其部分原理简化如图所示。两光纤可等效为圆柱状玻璃丝
、,相距为,直径均为,折射率为。、 下端横截
面平齐且与被测物体表面平行。激光在 内多次全反射后从下端
面射向被测物体,经被测物体表面镜面反射至下端面, 下端面
被照亮的面积与玻璃丝下端面与被测物体距离有关。
(1) 从下端面出射的光与竖直方向的最大偏角为,求 的正弦值;
【答案】
【解析】 设激光照射在玻璃丝内的临界角为 ,出射光与竖直方向偏角最大时入射角为
,则由折射定律得 。
由几何关系得 ,
由全反射的临界角公式可得 ,
联立解得 。
(2) 被测物体自上而下微小移动,使 下端面从刚能接收反射激光到恰好全部被照亮,
求玻璃丝下端面到被测物体距离 的相应范围(只考虑在被测物体表面反射一次的光线)。
【答案】
【解析】 设 下端面刚能接收到反射光时与被测物体表面的距离为
,下端面恰好全部被照亮时与被测物体表面的距离为 ,如图所示,
则由反射定律和几何关系得, ,
解得, ,
则 。
10.(2024陕西铜川模拟)光刻机是半导体工业耀眼的明珠,是生产
大模集成电路的核心设备。光刻机物镜投影原理简化图如图所示,
其中为等腰直角玻璃三棱镜截面,直角边长为,为 边
的中点,半球形玻璃砖的半径为,为球心, 为半球形玻璃砖
截面的对称轴,点到三棱镜边距离为。条形平行光线、 间
距为,从左侧垂直 边射入三棱镜,经反射后向下进入半球形
玻璃砖,反射光线关于轴线对称,最后聚焦到硅片上 点。已知棱镜和玻璃砖的折
射率为,光在真空中的速度为 ,求:
(1) 、 两点间距离;
【答案】
【解析】 设光在三棱镜中发生全反射的临界角为,由 ,
可得(【点拨】 ,所以 。),
. .
光在三棱镜中发生全反射。根据题意画出光线 在半球形玻璃砖的入
射光线和出射光线,如图所示。设光射入半球形玻璃砖的入射角为 ,
由几何关系得(【点拨】过点作的垂线,交
于点,平行光线、间距为,则, ,则在直角
三角形中可计算出 。
再次提醒计算 时可不用写出计算过程,直接写“由几何关系可得
”即可。),
得 ,
. .
由折射定律有,得(【大招运用】看见折射率 ,联想到
,可快速得出折射角 。)。
由几何关系得光线在半球形玻璃砖出射面的入射角,折射角为 ,
由折射定律,得 ,
可得, 。
. .
(2) 光从进入三棱镜到聚焦在点 的时间。
【答案】
【解析】 光在三棱镜及半球形玻璃砖内的速度 ,
光在三棱镜内的传播路程 ,
在半球形玻璃砖内的传播路程 ,
光在空气中的传播路程
,
光从进入三棱镜到聚焦在点 的时间
。
专题十四 光学
考向一 光的折射和全反射
2025年高考物理专题复习资料
考点切片
考点1 光的折射和折射率
1.(2024贵州卷)一种测量液体折射率的 形容器,由两块材
质相同的直角棱镜粘合并封闭其前后两端制作而成。容器中
盛有某种液体,一激光束从左边棱镜水平射入,通过液体后
从右边棱镜射出,其光路如图所示。设棱镜和液体的折射率
分别为、,光在棱镜和液体中的传播速度分别为、 ,
则( )
A
A., B., C., D.,
【解析】 由题图可知光从棱镜进入液体中时,入射角小于折射角,根据折射定律可知
,由折射率与速度的关系式可得 ,故选A。
跳跳学长 敲黑板
定义式 (不论光从真空斜射入介质,还是从介质斜射入真空, 总是真
空中的光线与法线间的夹角, 总是介质中的光线与法线间的夹角。
影响因素 折射率由介质本身的性质决定,与入射角的大小无关。折射率还与光的
频率有关,同一种介质中,光的频率越大,介质对其折射率越大,光在该介
质中的传播速度越小。
与光速的关系 , 是光在该介质中的传播速度。
提醒 折射率与介质的密度没有关系,光密介质不是指密度大的介质。
2.(2024重庆卷)某同学设计了一种测量液体折射率的方案。过
容器中心轴线的剖面图如图所示,其宽度为 ,让单色光在此
剖面内从空气入射到液体表面的中心。调整入射角,当反射光与
折射光垂直时,测出竖直器壁上的反射光点与液体表面的距离 ,
就能得到液体的折射率 。忽略器壁厚度,由该方案可知( )
B
A.若,则 B.若,则
C.若,则 D.若,则
【解析】
根据几何关系画出光路图,如图所示,标注入射角,折射角 ,根据折射定律可得 。 ________________________________________ 若,则 。 A( )
若,则 。 B(√)
若,则 。 C( )
若,则 。 D( )
3.[多选](2024湖南模拟预测)雨过天晴,
空气中悬浮着大量小水滴,若太阳光从背后
近乎水平入射,观察者便会看到彩虹,如图
甲所示。有时能够同时观察到两道彩虹,内
层彩虹被称为“虹”,外层彩虹被称为“霓”。
BC
A.“虹”对应光路图中1级光,色序表现为“内红外紫”
B.“霓”对应光路图中2级光,色序表现为“内红外紫”
C.对同一束入射日光,产生“虹”现象时红光在水滴内传播时间小于紫光
D.对同一束入射日光,产生“虹”现象时紫光在水滴内传播时间小于红光
这是由阳光在小水滴内部反射次数不同导致的。彩虹现象形成时,阳光在小水滴中的大
致光路如图乙所示。关于彩虹现象,下列说法正确的有( )
【解析】 由题可知,内层彩虹被称为“虹”,所以对应光路图
中1级光。根据紫光频率大于红光,可知紫光入射小水滴时折射率
较大,由此作出“虹”的光路图如图所示,色序表现为“内紫外红”。
“霓”的产生和“虹”类似,但日光在水滴中反射两次,对应光路
图中2级光,色序排列表现与“虹”相反,表现为“内红外紫”。
对同一束入射光,产生“虹”现象时,设折射角为 ,球形
水滴的半径为,有, ,光传播的路程为 ,则光在水滴中的传
播时间为
,红光和紫光有相同的入射角 ,而水
滴对紫光的折射率大于对红光的折射率,则紫光在水滴内的传播时间大于红光在水滴内
的传播时间。
考点2 光的全反射
4.(2024江苏南通模拟)如图所示,竖直挡板有镂空字母“ ”,全
反射棱镜的左侧面与挡板平行,右侧面与水平面的夹角为 ,
一水平光束从挡板左侧入射,从上往下看,穿过棱镜后在其下方
水平光屏 上形成的图样是( )
C
A. B. C. D.
【解析】 光透过镂空部分后,会在全反射棱镜的倾斜面
处发生全反射,如图所示。一水平光束从挡板左侧入射,根据
光路可以确定“”的上半部分靠近边,下半部分靠近 边。
5.[多选](2025安徽名校联考)水底灯是水中环境常用的灯具之一,在夜间可以营造
出非常美丽的水下场景,增加水下的浪漫感和视觉效果。某公园水池底部安装了可视为
点光源的灯和 灯,两灯到水面的距离相等,如图所示。两灯发出不同颜色的光,分
别为光、光,从每盏灯的正上方观察,发现灯的视深大于 灯的视深,则下列说法
正确的是( )
AC
A.水对光的折射率比对 光的折射率要小
B.在水中,光的传播速度大于 光的传播速度
C.灯照亮水面的面积大于 灯照亮的面积
D.将光和光通过相同的双缝干涉装置, 光的干涉条纹间距
较大
图1
【解析】 设实际深度为,视深为 ,作出光路图如图1所示。
根据折射率定义式有,结合几何关系有 ,
由于从正上方观察,与很小,则有 ,
, 解得,故水对光的折射率比对 光的折射率要
小。
根据可知,在水中光的传播速度小于 光的传播速度。
图2
如图2所示,灯照亮水面的面积
,而,所以 灯照亮水面
的面积比 灯的大。
光的折射率较小,则频率较小,根据,可得 光的波
长较长,由 可知, 光的干涉条纹间距较大。
6.(2024浙江温州模拟)如图甲所示,有一玻璃砖侧面为直角三角形,角 为直角,
边上有一点光源,光源发出的光波长可调。光在玻璃砖上发生全反射的临界角为 ,
在边上有光射出的长度为,作出 图像,如图乙所示。若直线1的斜率为
,直线2在纵轴上的截距为,不考虑二次反射,则 的长度为( )
B
A. B. C. D.
【解析】 过向作垂线,长为,如图所示,利用几何关系可知 ,当临界角
大于时,下方出射的光线能到达点,关系满足 ,利用题
中已知斜率和截距,由①②两个方程得出,(【点拨】函数 对
应图线1,斜率,函数对应图线2,纵截距 。),
则,因此 ,故选B。
. .
考点3 光的折射和全反射的综合应用
大招72 对应练习
解题觉醒
1.题型特征:画光路图,利用几何分析,求长度、角度或折射率
2.规律总结
(1)起手先写“由几何关系”。
(2)如果已知折射率
(3)只要光从光密介质射入光疏介质,一定要验证是否有全反射。
(4)留意
(5)圆内很容易出现等腰三角形。
7.(2024全国甲卷)一玻璃柱的折射率,其横截面为四分之一圆,圆的半径为 ,
如图所示。截面所在平面内,一束与边平行的光线从圆弧入射。入射光线与 边的
距离由小变大,距离为时,光线进入柱体后射到边恰好发生全反射。求此时与
的比值。
【答案】
【解析】 根据题意可画出入射光线与边的距离为 时的光路图,如图所示
则由折射定律有
,
由全反射临界角公式有
。
由几何关系可得(【点拨】物理当中用到的一些简单几何关系时不需要具体说明什么样
的几何关系,直接写“由几何关系可得”,并写出结论即可。所以小伙伴们,要想学好物理,一
些数学知识是必不可少的。曾经还有人说过如果一个人可以称得上是物理学家,那他一
定也是一个数学家。)
,
,
联立解得 。
8.(2022湖南卷)如图所示,某种防窥屏由
透明介质和对光完全吸收的屏障构成,其中
屏障垂直于屏幕平行排列,可实现对像素单
元可视角度的控制(可视角度 定义为
某像素单元发出的光在图示平面内折射到空
(1) 若把发光像素单元视为点光源,要求可视角度控制为,求屏障的高度 ;
【答案】
气后最大折射角的2倍)。透明介质的折射率,屏障间隙 。发光像素单
元紧贴屏下,位于相邻两屏障的正中间,不考虑光的衍射。
(2) 若屏障高度,且发光像素单元的宽度不能忽略,求像素单元宽度 最
小为多少时,其可视角度刚好被扩为 (只要看到像素单元的任意一点,即视为
能看到该像素单元)。
【答案】
【解析】
1.构建模型 (1)长方体透明介质,可视角度为 时的光路图如图1所示——折射
角为 ;
___________________________________
图1
1.构建模型 (2)可视角度为 时的光路图如图2所示——折射角为
_______________________________________
图2
2.定角度 第(1)问入射角为,折射角为 ;
第(2)问入射角为,折射角为
3.根据折射定 律和几何关系 列方程 (1)由几何关系则,,解得 ,
;
(2)发光像素单元最左端与屏障的距离为 ,像素
单元宽度最小为
9.(2023山东卷)一种反射式光纤位移传感器可以实现微小位移测
量,其部分原理简化如图所示。两光纤可等效为圆柱状玻璃丝
、,相距为,直径均为,折射率为。、 下端横截
面平齐且与被测物体表面平行。激光在 内多次全反射后从下端
面射向被测物体,经被测物体表面镜面反射至下端面, 下端面
被照亮的面积与玻璃丝下端面与被测物体距离有关。
(1) 从下端面出射的光与竖直方向的最大偏角为,求 的正弦值;
【答案】
【解析】 设激光照射在玻璃丝内的临界角为 ,出射光与竖直方向偏角最大时入射角为
,则由折射定律得 。
由几何关系得 ,
由全反射的临界角公式可得 ,
联立解得 。
(2) 被测物体自上而下微小移动,使 下端面从刚能接收反射激光到恰好全部被照亮,
求玻璃丝下端面到被测物体距离 的相应范围(只考虑在被测物体表面反射一次的光线)。
【答案】
【解析】 设 下端面刚能接收到反射光时与被测物体表面的距离为
,下端面恰好全部被照亮时与被测物体表面的距离为 ,如图所示,
则由反射定律和几何关系得, ,
解得, ,
则 。
10.(2024陕西铜川模拟)光刻机是半导体工业耀眼的明珠,是生产
大模集成电路的核心设备。光刻机物镜投影原理简化图如图所示,
其中为等腰直角玻璃三棱镜截面,直角边长为,为 边
的中点,半球形玻璃砖的半径为,为球心, 为半球形玻璃砖
截面的对称轴,点到三棱镜边距离为。条形平行光线、 间
距为,从左侧垂直 边射入三棱镜,经反射后向下进入半球形
玻璃砖,反射光线关于轴线对称,最后聚焦到硅片上 点。已知棱镜和玻璃砖的折
射率为,光在真空中的速度为 ,求:
(1) 、 两点间距离;
【答案】
【解析】 设光在三棱镜中发生全反射的临界角为,由 ,
可得(【点拨】 ,所以 。),
. .
光在三棱镜中发生全反射。根据题意画出光线 在半球形玻璃砖的入
射光线和出射光线,如图所示。设光射入半球形玻璃砖的入射角为 ,
由几何关系得(【点拨】过点作的垂线,交
于点,平行光线、间距为,则, ,则在直角
三角形中可计算出 。
再次提醒计算 时可不用写出计算过程,直接写“由几何关系可得
”即可。),
得 ,
. .
由折射定律有,得(【大招运用】看见折射率 ,联想到
,可快速得出折射角 。)。
由几何关系得光线在半球形玻璃砖出射面的入射角,折射角为 ,
由折射定律,得 ,
可得, 。
. .
(2) 光从进入三棱镜到聚焦在点 的时间。
【答案】
【解析】 光在三棱镜及半球形玻璃砖内的速度 ,
光在三棱镜内的传播路程 ,
在半球形玻璃砖内的传播路程 ,
光在空气中的传播路程
,
光从进入三棱镜到聚焦在点 的时间
。
同课章节目录
