27.2.3 切线性质与判定 课件(共20张PPT)
文档属性
| 名称 | 27.2.3 切线性质与判定 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 889.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-18 12:55:15 | ||
图片预览






文档简介
(共20张PPT)
九年级下册数学
27.2.3 切线性质与判定
学习目标
学习目标:
1、 理解并会判断什么是切线。
2、理解并会正确运用切线的判定定理和性质
探究发现
自学指导:
请同学们认真看P51--P52练习上面的内容。要求:
认真思考以下3个小问题并完成P51“做一做”:
(1)过半径OA的外端点A画一条直线l( 垂直除外),与圆有几个公共点
(2)画一条直线l垂直于半径OA(直线l不经过点 A),与圆有几个公共点
(3)经过半径端点O画一条直线l垂直于这条半径,与圆有几个公共点
O
r
l
A
O
r
l
A
O
r
l
A
直线l时圆的切线吗
探究发现
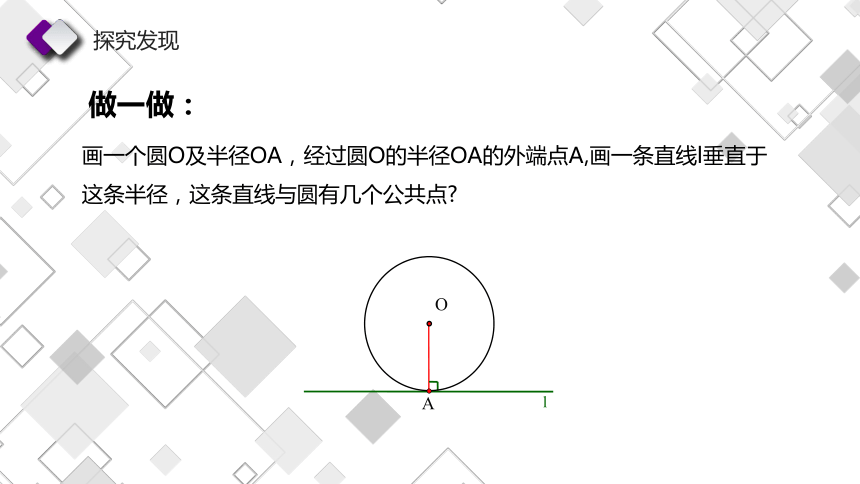
做一做:
画一个圆O及半径OA,经过圆O的半径OA的外端点A,画一条直线l垂直于这条半径,这条直线与圆有几个公共点
O
A
l
探究发现
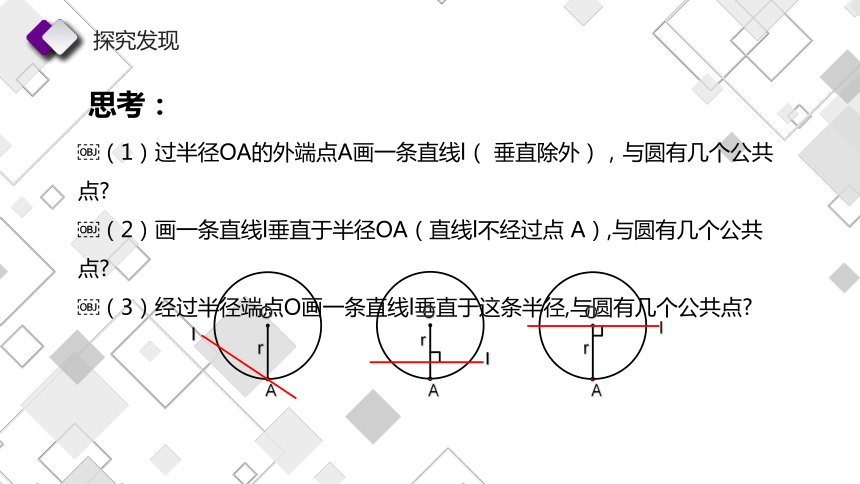
思考:
(1)过半径OA的外端点A画一条直线l( 垂直除外),与圆有几个公共点
(2)画一条直线l垂直于半径OA(直线l不经过点 A),与圆有几个公共点
(3)经过半径端点O画一条直线l垂直于这条半径,与圆有几个公共点
O
r
l
A
O
r
l
A
O
r
l
A
归纳总结
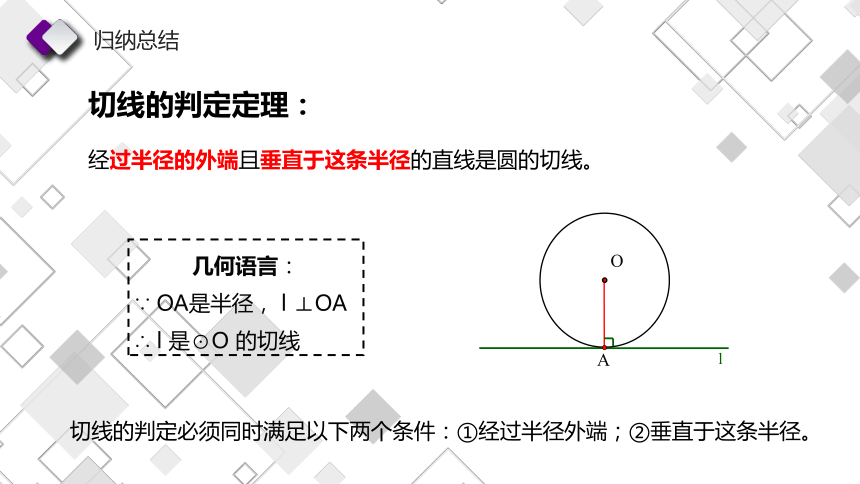
切线的判定定理:
经过半径的外端且垂直于这条半径的直线是圆的切线。
O
A
l
几何语言:
∵ OA是半径, l ⊥OA
∴ l 是⊙O 的切线
切线的判定必须同时满足以下两个条件:①经过半径外端;②垂直于这条半径。
典例精讲
例1.如图,已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
判断直线AB与⊙O的位置关系,并说明理由。
O
B
A
C
证明:直线AB与⊙O相切,理由如下:。
连结OC
∵OA=OB,CA=CB
∴OC⊥AB
∵OC是⊙O的半径
∴直线AB与⊙O相切
【分析】
①直线AB经过⊙O上的点C
②直线AB⊥OC
直线AB与⊙O相切,切点是点C。
典例精讲
例1.如图,已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
判断直线AB与⊙O的位置关系,并说明理由。
例题总结:
切线判定定理:
已知:①直线过半径外端
论证:②直线垂直于半径
直线是该圆的切线
连半径,证垂直,得切线
典例精讲
例1.如图, 为 ⊙ 的直径,点 为 ⊙ 上一点,连接 ,点
为 的中点,过点 作 // ,交 的延长线于点 .
求证: 与 ⊙ 相切.
典例精讲
例2.如图,⊙O的半径为4,OA⊥AB于点O,OC⊥AB于点C,OA=4,OB=2求证:AB与⊙O相切
O
B
A
C
【分析】
①直线AB⊥OC于点C
②OC为⊙O的半径
直线AB与⊙O相切,切点是点C。
典例精讲
例2.如图,⊙O的半径为4,OA⊥AB于点O,OC⊥AB于点C,OA=4,OB=2求证:AB与⊙O相切
例题总结:
切线判定定理:
已知:①直线垂直于线段OC
论证:②直线过半径外端
直线是该圆的切线
作垂直,证半径,得切线
探究发现
探究切线的性质:
问题一:你能指出切线判定定理的题设和结论?
切线的判定定理:
经过半径的外端且垂直于这条半径的直线是圆的切线。
探究发现
探究切线的性质:
问题一:你能指出切线判定定理的题设和结论?
如果一条直线经过一个圆半径的外端,并且垂直于这条半径。
那么这条直线是这个圆的切线
题设
结论
问题二:你能写出切线判定定理的逆命题吗
逆命题:如果一条直线是一个圆的切线,那么这条直线经过圆一条半径的外端,并且垂直于这条半径。
探究发现
探究切线的性质:
已知:直线L与⊙O 相切于A , 求证:L⊥OA
O
A
C
l
反证法:
证明:假设直线L与⊙O 不垂直
过点C做OC⊥L,垂足为点C
根据垂线段最短可知OC<OA
即圆心到直线的距离OC小于半径OA
∴直线L与圆O相交
与已知条件“直线L与圆O相切” 矛盾
∴ L垂直于OA
归纳总结
O
A
l
几何语言:
∵ l是⊙O的切线,OA是半径
∴ l ⊥OA
已知直线与圆相切,连结圆心和切点,得到直线垂直于半径。
简记为:知切线,连半径,得垂直。
切线的性质定理:
如果一条直线是一个圆的切线,那么这条直线经过圆一条半径的外端,并且垂直于这条半径。
圆的切线垂直于经过切点的半径。
典例精讲
例3.如图,AB 是半圆O 直径,CD为半圆O的一条切线 , C为切点,
AD⊥CD,垂足为点D
求证:AC 平分∠DAB.
A
B
O
C
D
中考链接
1.[2023河南14题3分]如图, 与 相切于点 , 交 于点 ,点 在 上,且 .若 , ,则 的长为 .
课堂小结
课堂总结
切线
性质
1.定义法:与圆只有一个交点的直线是圆的切线
判定
2.距离法:到圆心的距离等于该圆半径的直线是圆的切线
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线
1.性质定理:圆的切线垂直于经过切点的半径
2.直线与圆只有一个交点
3.直线到圆心的距离等于半径
分层作业
A组:课本P52练习1、2、3、4.
B组:课本P52练习2、3.
B组:课本P52练习1、4.
九年级下册数学
27.2.3 切线性质与判定
学习目标
学习目标:
1、 理解并会判断什么是切线。
2、理解并会正确运用切线的判定定理和性质
探究发现
自学指导:
请同学们认真看P51--P52练习上面的内容。要求:
认真思考以下3个小问题并完成P51“做一做”:
(1)过半径OA的外端点A画一条直线l( 垂直除外),与圆有几个公共点
(2)画一条直线l垂直于半径OA(直线l不经过点 A),与圆有几个公共点
(3)经过半径端点O画一条直线l垂直于这条半径,与圆有几个公共点
O
r
l
A
O
r
l
A
O
r
l
A
直线l时圆的切线吗
探究发现
做一做:
画一个圆O及半径OA,经过圆O的半径OA的外端点A,画一条直线l垂直于这条半径,这条直线与圆有几个公共点
O
A
l
探究发现
思考:
(1)过半径OA的外端点A画一条直线l( 垂直除外),与圆有几个公共点
(2)画一条直线l垂直于半径OA(直线l不经过点 A),与圆有几个公共点
(3)经过半径端点O画一条直线l垂直于这条半径,与圆有几个公共点
O
r
l
A
O
r
l
A
O
r
l
A
归纳总结
切线的判定定理:
经过半径的外端且垂直于这条半径的直线是圆的切线。
O
A
l
几何语言:
∵ OA是半径, l ⊥OA
∴ l 是⊙O 的切线
切线的判定必须同时满足以下两个条件:①经过半径外端;②垂直于这条半径。
典例精讲
例1.如图,已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
判断直线AB与⊙O的位置关系,并说明理由。
O
B
A
C
证明:直线AB与⊙O相切,理由如下:。
连结OC
∵OA=OB,CA=CB
∴OC⊥AB
∵OC是⊙O的半径
∴直线AB与⊙O相切
【分析】
①直线AB经过⊙O上的点C
②直线AB⊥OC
直线AB与⊙O相切,切点是点C。
典例精讲
例1.如图,已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
判断直线AB与⊙O的位置关系,并说明理由。
例题总结:
切线判定定理:
已知:①直线过半径外端
论证:②直线垂直于半径
直线是该圆的切线
连半径,证垂直,得切线
典例精讲
例1.如图, 为 ⊙ 的直径,点 为 ⊙ 上一点,连接 ,点
为 的中点,过点 作 // ,交 的延长线于点 .
求证: 与 ⊙ 相切.
典例精讲
例2.如图,⊙O的半径为4,OA⊥AB于点O,OC⊥AB于点C,OA=4,OB=2求证:AB与⊙O相切
O
B
A
C
【分析】
①直线AB⊥OC于点C
②OC为⊙O的半径
直线AB与⊙O相切,切点是点C。
典例精讲
例2.如图,⊙O的半径为4,OA⊥AB于点O,OC⊥AB于点C,OA=4,OB=2求证:AB与⊙O相切
例题总结:
切线判定定理:
已知:①直线垂直于线段OC
论证:②直线过半径外端
直线是该圆的切线
作垂直,证半径,得切线
探究发现
探究切线的性质:
问题一:你能指出切线判定定理的题设和结论?
切线的判定定理:
经过半径的外端且垂直于这条半径的直线是圆的切线。
探究发现
探究切线的性质:
问题一:你能指出切线判定定理的题设和结论?
如果一条直线经过一个圆半径的外端,并且垂直于这条半径。
那么这条直线是这个圆的切线
题设
结论
问题二:你能写出切线判定定理的逆命题吗
逆命题:如果一条直线是一个圆的切线,那么这条直线经过圆一条半径的外端,并且垂直于这条半径。
探究发现
探究切线的性质:
已知:直线L与⊙O 相切于A , 求证:L⊥OA
O
A
C
l
反证法:
证明:假设直线L与⊙O 不垂直
过点C做OC⊥L,垂足为点C
根据垂线段最短可知OC<OA
即圆心到直线的距离OC小于半径OA
∴直线L与圆O相交
与已知条件“直线L与圆O相切” 矛盾
∴ L垂直于OA
归纳总结
O
A
l
几何语言:
∵ l是⊙O的切线,OA是半径
∴ l ⊥OA
已知直线与圆相切,连结圆心和切点,得到直线垂直于半径。
简记为:知切线,连半径,得垂直。
切线的性质定理:
如果一条直线是一个圆的切线,那么这条直线经过圆一条半径的外端,并且垂直于这条半径。
圆的切线垂直于经过切点的半径。
典例精讲
例3.如图,AB 是半圆O 直径,CD为半圆O的一条切线 , C为切点,
AD⊥CD,垂足为点D
求证:AC 平分∠DAB.
A
B
O
C
D
中考链接
1.[2023河南14题3分]如图, 与 相切于点 , 交 于点 ,点 在 上,且 .若 , ,则 的长为 .
课堂小结
课堂总结
切线
性质
1.定义法:与圆只有一个交点的直线是圆的切线
判定
2.距离法:到圆心的距离等于该圆半径的直线是圆的切线
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线
1.性质定理:圆的切线垂直于经过切点的半径
2.直线与圆只有一个交点
3.直线到圆心的距离等于半径
分层作业
A组:课本P52练习1、2、3、4.
B组:课本P52练习2、3.
B组:课本P52练习1、4.
