华师大版(2024)数学七下5.3实践与探索(第3课时) 同步教学课件(共22张PPT)
文档属性
| 名称 | 华师大版(2024)数学七下5.3实践与探索(第3课时) 同步教学课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 896.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-18 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
(华师大版)七年级
下
5.3实践与探索
(第3课时)
一元一次方程
第5章
“五”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.通过分析具体问题中的工程关系,建立方程解决问题.
2.通过分析具体问题中的行程关系,建立方程解决问题.
3.进一步了解一元一次方程在解决实际问题中的应用,感受具体问题中数量之间的关系和变化规律.
新知导入
做某件工作,甲单独做要 8 时才能完成,乙单独做要 12 时才能
完成,问:
①甲做 1 时完成全部工作量的几分之几? .
②乙做 1 时完成全部工作量的几分之几? .
③甲、乙合做 1 时完成全部工作量的几分之几? .
④甲做 x 时完成全部工作量的几分之几? .
新知讲解
问题3:
课外活动时李老师来教室布置作业,有一道题目只写了“某工厂需制作一块广告牌,请来两名工人,已知师傅单独完成需4天,徒弟单独完成需6天”就停住了,片刻后,同学们带着疑惑的目光,窃窃私语:“这道题目不完整呀!”“要求什么呢 ”……
李老师开口了:“同学们的疑问是有道理的.
今天我就是要请同学们自己来提出问题,
请发挥你们的想象力,把这道题目补充完整.”
新知讲解
问题3:
小明抢先说:“让我试一试.”于是,上去添了:“两人合作需要几天完成 ”
有同学反对:“这太简单了!”但也引起了大家的兴趣,于是各自试了起来:
有考虑一人先做几天再让另一人做的,有考虑两人先合作再一人离开的,也有考虑两人合作完成后的报酬问题的……
李老师选了两位同学的问题,综合后,在黑板上写出:现由徒弟先做1天,再两人合作,完成后共得到报酬900元.如果按各人完成的工作量计算报酬,那么该如何分配
试解答这一问题,并和同学交流各自的做法.
新知讲解
问题3:
题目1:某工厂需制作一块广告牌,请来两名工人,已知师傅单独完成需4天,徒弟单独完成需6天,两人合作需要几天完成
解:设两人合作需要 天完成,
根据题意,得,解得 .
答:两人合作需要 天完成.
新知讲解
问题3:
题目2:某工厂需制作一块广告牌,请来两名工人,已知师傅单独完成需4天,徒弟单独完成需6天,现由徒弟先做1天,再两人合作,完成后共得到报酬900元.如果按各人完成的工作量计算报酬,那么该如何分配
解:设两人合作需x天完成.
由题意,得方程
解得 x=2
所以
所以师傅和徒弟各分得450元.
新知讲解
工程问题:
1. 基本关系式:工作量=工作效率 ×工作时间,
工作时间=,工作效率= .
2. 找相等关系一般有如下规律:在工作量、工作效率、工作时间这三个量中,如果一个量已知,另一个量设元,那么就从第三个量找相等关系列方程 .
新知讲解
☆注意:
1. 当问题中总工作量未知而又不求总工作量时,通常把总工作量看成整体 1.
2. 常见的相等关系:总工作量 = 各部分工作量之和 .
新知讲解
行程问题:
基本关系式:(1)路程=速度×时间;(2)时间=路程÷速度;
(3)速度=路程÷时间.
新知讲解
行程问题:
相遇问题:甲路程+乙路程=总路程
追击问题:快车路程-慢车路程=路程差
航行问题:
逆水速度=船速-水速
环形跑道问题:快的路程-慢的路程=1圈(第1次相遇)
顺水速度=船速+水速
【知识技能类作业】必做题:
课堂练习
1.某厂为支援灾区赶制一批帐篷,第一天生产了总数的25%,第二天生产了总数的,两天共生产了990顶,这批帐篷一共有( )
A. 1200顶 B. 1400顶 C. 1600顶 D. 1800顶
D
【知识技能类作业】必做题:
课堂练习
2.课外活动中一些学生分组参加活动,原来每组8人,后来重新编组,每组12人,这样就比原来减少2组.则这些学生共有____人.
48
3.七年级甲、乙两个班共有学生100人,其中参加数学活动小组的有42人,已知甲班有的学生参加数学活动小组,乙班有的学生参加数学活动小组,分别求甲、乙两个班的学生人数.
【知识技能类作业】必做题:
课堂练习
解:设甲班的学生人数是x,则乙班的学生人数是100-x.
由题意,得x+(100-x)=42,解得x=48.
经检验,符合题意.所以100-x=100-48=52.
所以甲班的学生人数是48,乙班的学生人数是52。
【知识技能类作业】选做题:
课堂练习
4.已知甲、乙、丙三人每人都有一些钱,其中甲的钱数是乙的2倍,乙比丙多1元,丙比甲少11元,则三人共有( )
A. 30元 B. 33元 C. 36元 D. 39元
D
5. 已知某商店有两件进价不同的衣服都卖了210元,其中一件盈利50%,另一件亏损30%,在这两件衣服的买卖中,这家商店盈亏情况是 ( )
A. 盈利10元 B. 亏损10元 C. 盈利20元 D. 亏损20元
【知识技能类作业】选做题:
课堂练习
D
【综合拓展类作业】
课堂练习
6. 某商场举办家电促销活动,本次活动中的家电消费券为单笔交易满600元立减128元(每次只能使用一张).某品牌电饭煲每台按进价提高50%后标价,若按标价的八折销售,某顾客在购买该电饭煲时,使用一张家电消费券后,又付现金568元,求该电饭煲每台的进价.
解:设该电饭煲每台的进价为x元,则每台的标价为(1+50%)x元,
售价为80%×(1+50%)x元.
根据题意,得80%×(1+50%)x-128=568,解得x=580.经检验,符合题意.
所以该电饭煲每台的进价为580元
课堂总结
1.工程问题:
基本关系式:工作量=工作效率 ×工作时间,
工作时间=,工作效率= .
2.行程问题:
基本关系式:(1)路程=速度×时间;(2)时间=路程÷速度;
(3)速度=路程÷时间.
板书设计
1.工程问题:
基本关系式:工作量=工作效率 ×工作时间,
工作时间=,工作效率= .
2.行程问题:
基本关系式:(1)路程=速度×时间;(2)时间=路程÷速度;
(3)速度=路程÷时间.
课题:5.3实践与探索(第3课时)
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
5.3实践与探索
(第3课时)
一元一次方程
第5章
“五”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.通过分析具体问题中的工程关系,建立方程解决问题.
2.通过分析具体问题中的行程关系,建立方程解决问题.
3.进一步了解一元一次方程在解决实际问题中的应用,感受具体问题中数量之间的关系和变化规律.
新知导入
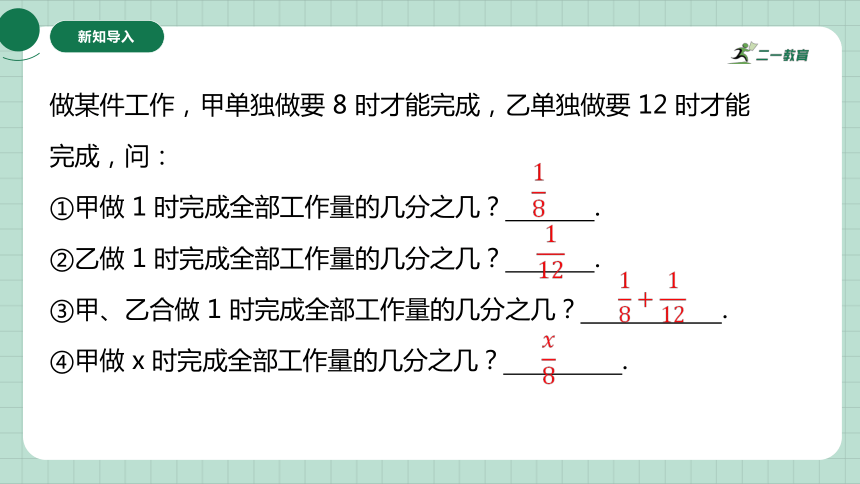
做某件工作,甲单独做要 8 时才能完成,乙单独做要 12 时才能
完成,问:
①甲做 1 时完成全部工作量的几分之几? .
②乙做 1 时完成全部工作量的几分之几? .
③甲、乙合做 1 时完成全部工作量的几分之几? .
④甲做 x 时完成全部工作量的几分之几? .
新知讲解
问题3:
课外活动时李老师来教室布置作业,有一道题目只写了“某工厂需制作一块广告牌,请来两名工人,已知师傅单独完成需4天,徒弟单独完成需6天”就停住了,片刻后,同学们带着疑惑的目光,窃窃私语:“这道题目不完整呀!”“要求什么呢 ”……
李老师开口了:“同学们的疑问是有道理的.
今天我就是要请同学们自己来提出问题,
请发挥你们的想象力,把这道题目补充完整.”
新知讲解
问题3:
小明抢先说:“让我试一试.”于是,上去添了:“两人合作需要几天完成 ”
有同学反对:“这太简单了!”但也引起了大家的兴趣,于是各自试了起来:
有考虑一人先做几天再让另一人做的,有考虑两人先合作再一人离开的,也有考虑两人合作完成后的报酬问题的……
李老师选了两位同学的问题,综合后,在黑板上写出:现由徒弟先做1天,再两人合作,完成后共得到报酬900元.如果按各人完成的工作量计算报酬,那么该如何分配
试解答这一问题,并和同学交流各自的做法.
新知讲解
问题3:
题目1:某工厂需制作一块广告牌,请来两名工人,已知师傅单独完成需4天,徒弟单独完成需6天,两人合作需要几天完成
解:设两人合作需要 天完成,
根据题意,得,解得 .
答:两人合作需要 天完成.
新知讲解
问题3:
题目2:某工厂需制作一块广告牌,请来两名工人,已知师傅单独完成需4天,徒弟单独完成需6天,现由徒弟先做1天,再两人合作,完成后共得到报酬900元.如果按各人完成的工作量计算报酬,那么该如何分配
解:设两人合作需x天完成.
由题意,得方程
解得 x=2
所以
所以师傅和徒弟各分得450元.
新知讲解
工程问题:
1. 基本关系式:工作量=工作效率 ×工作时间,
工作时间=,工作效率= .
2. 找相等关系一般有如下规律:在工作量、工作效率、工作时间这三个量中,如果一个量已知,另一个量设元,那么就从第三个量找相等关系列方程 .
新知讲解
☆注意:
1. 当问题中总工作量未知而又不求总工作量时,通常把总工作量看成整体 1.
2. 常见的相等关系:总工作量 = 各部分工作量之和 .
新知讲解
行程问题:
基本关系式:(1)路程=速度×时间;(2)时间=路程÷速度;
(3)速度=路程÷时间.
新知讲解
行程问题:
相遇问题:甲路程+乙路程=总路程
追击问题:快车路程-慢车路程=路程差
航行问题:
逆水速度=船速-水速
环形跑道问题:快的路程-慢的路程=1圈(第1次相遇)
顺水速度=船速+水速
【知识技能类作业】必做题:
课堂练习
1.某厂为支援灾区赶制一批帐篷,第一天生产了总数的25%,第二天生产了总数的,两天共生产了990顶,这批帐篷一共有( )
A. 1200顶 B. 1400顶 C. 1600顶 D. 1800顶
D
【知识技能类作业】必做题:
课堂练习
2.课外活动中一些学生分组参加活动,原来每组8人,后来重新编组,每组12人,这样就比原来减少2组.则这些学生共有____人.
48
3.七年级甲、乙两个班共有学生100人,其中参加数学活动小组的有42人,已知甲班有的学生参加数学活动小组,乙班有的学生参加数学活动小组,分别求甲、乙两个班的学生人数.
【知识技能类作业】必做题:
课堂练习
解:设甲班的学生人数是x,则乙班的学生人数是100-x.
由题意,得x+(100-x)=42,解得x=48.
经检验,符合题意.所以100-x=100-48=52.
所以甲班的学生人数是48,乙班的学生人数是52。
【知识技能类作业】选做题:
课堂练习
4.已知甲、乙、丙三人每人都有一些钱,其中甲的钱数是乙的2倍,乙比丙多1元,丙比甲少11元,则三人共有( )
A. 30元 B. 33元 C. 36元 D. 39元
D
5. 已知某商店有两件进价不同的衣服都卖了210元,其中一件盈利50%,另一件亏损30%,在这两件衣服的买卖中,这家商店盈亏情况是 ( )
A. 盈利10元 B. 亏损10元 C. 盈利20元 D. 亏损20元
【知识技能类作业】选做题:
课堂练习
D
【综合拓展类作业】
课堂练习
6. 某商场举办家电促销活动,本次活动中的家电消费券为单笔交易满600元立减128元(每次只能使用一张).某品牌电饭煲每台按进价提高50%后标价,若按标价的八折销售,某顾客在购买该电饭煲时,使用一张家电消费券后,又付现金568元,求该电饭煲每台的进价.
解:设该电饭煲每台的进价为x元,则每台的标价为(1+50%)x元,
售价为80%×(1+50%)x元.
根据题意,得80%×(1+50%)x-128=568,解得x=580.经检验,符合题意.
所以该电饭煲每台的进价为580元
课堂总结
1.工程问题:
基本关系式:工作量=工作效率 ×工作时间,
工作时间=,工作效率= .
2.行程问题:
基本关系式:(1)路程=速度×时间;(2)时间=路程÷速度;
(3)速度=路程÷时间.
板书设计
1.工程问题:
基本关系式:工作量=工作效率 ×工作时间,
工作时间=,工作效率= .
2.行程问题:
基本关系式:(1)路程=速度×时间;(2)时间=路程÷速度;
(3)速度=路程÷时间.
课题:5.3实践与探索(第3课时)
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
