1.2 直角三角形定时训练(含解析)
文档属性
| 名称 | 1.2 直角三角形定时训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 250.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-18 00:00:00 | ||
图片预览


文档简介
1.2直角三角形定时训练 北师大版八年级数学下册
考试时间:30分钟;总分:100分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共5小题,满分25分,每小题5分)
1.若直角三角形的一个锐角等于40°,则它的另一个锐角等于( )
A.50° B.60° C.70° D.140°
2.在下列条件中不能判定△ABC为直角三角形的是( )
A.∠A=90°﹣∠C B.∠A=∠B﹣∠C
C.∠A=2∠B=3∠C D.∠A=∠B∠C
3.如图,在△ABC中,∠B=90°,AB=2、BC=4,四边形ADEC是正方形,则正方形ADEC的面积是( )
A.8 B.16 C.20 D.25
4.如图,Rt△ABC中,AB=3,BC=2,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A. B. C. D.
5.已知a,b,c是△ABC的三条边,则下列条件不能判定△ABC是直角三角形的是( )
A.a=2,b,c=3 B.∠A+∠B=∠C
C.(a+b)2+(a﹣b)2=2c2 D.∠A:∠B:∠C=2:3:4
二.填空题(共5小题,满分25分,每小题5分)
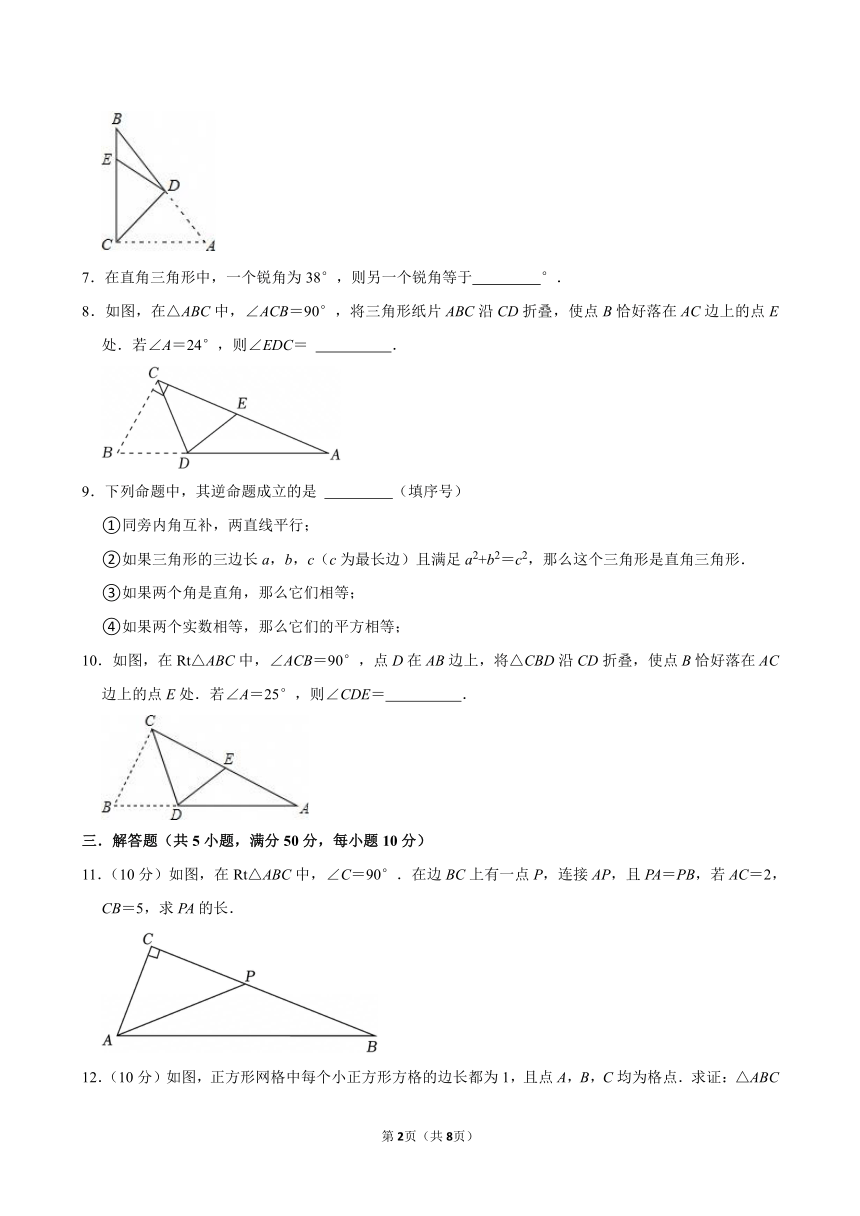
6.如图,在△ABC中,∠ACB=90°,∠A=52°,将其折叠,使点A落在边BC上的点E处,CA与CE重合,折痕为CD,则∠EDB的度数是 .
7.在直角三角形中,一个锐角为38°,则另一个锐角等于 °.
8.如图,在△ABC中,∠ACB=90°,将三角形纸片ABC沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=24°,则∠EDC= .
9.下列命题中,其逆命题成立的是 (填序号)
①同旁内角互补,两直线平行;
②如果三角形的三边长a,b,c(c为最长边)且满足a2+b2=c2,那么这个三角形是直角三角形.
③如果两个角是直角,那么它们相等;
④如果两个实数相等,那么它们的平方相等;
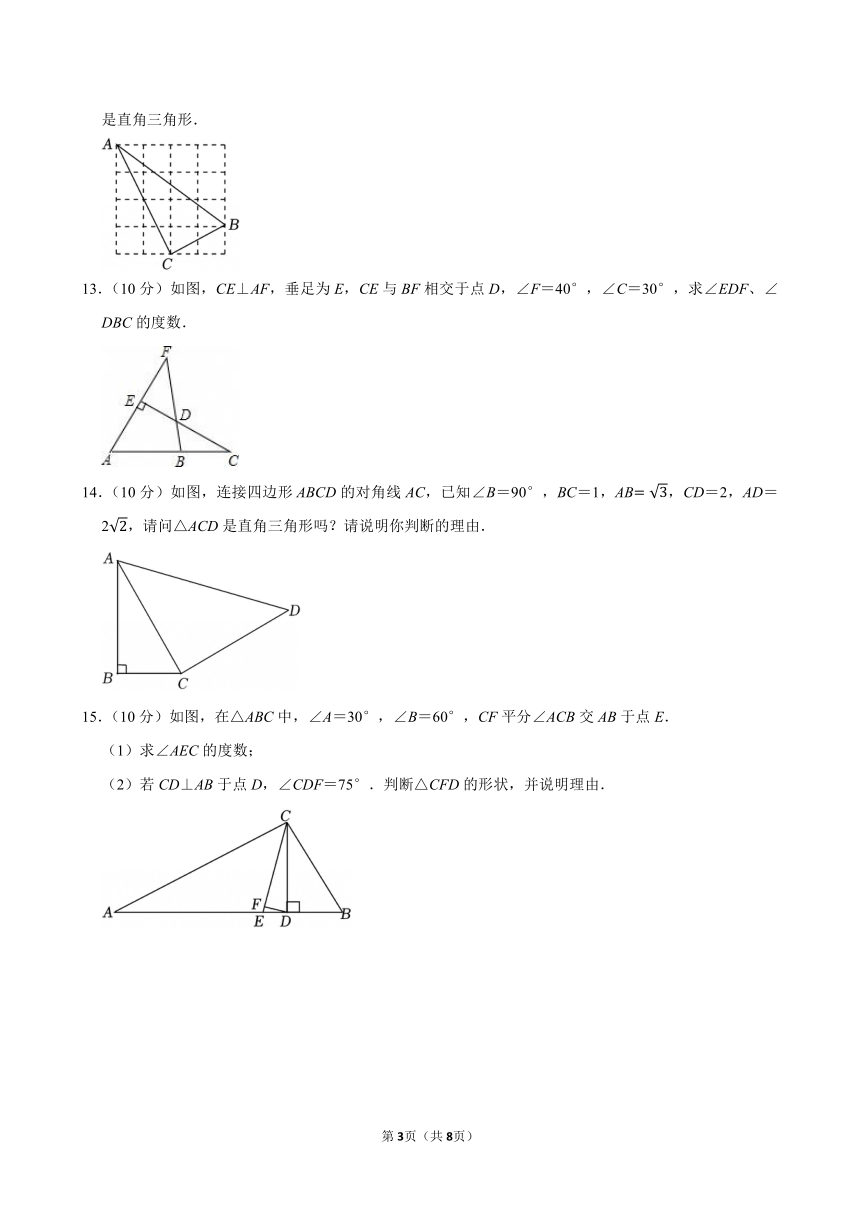
10.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=25°,则∠CDE= .
三.解答题(共5小题,满分50分,每小题10分)
11.(10分)如图,在Rt△ABC中,∠C=90°.在边BC上有一点P,连接AP,且PA=PB,若AC=2,CB=5,求PA的长.
12.(10分)如图,正方形网格中每个小正方形方格的边长都为1,且点A,B,C均为格点.求证:△ABC是直角三角形.
13.(10分)如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=40°,∠C=30°,求∠EDF、∠DBC的度数.
14.(10分)如图,连接四边形ABCD的对角线AC,已知∠B=90°,BC=1,AB,CD=2,AD=2,请问△ACD是直角三角形吗?请说明你判断的理由.
15.(10分)如图,在△ABC中,∠A=30°,∠B=60°,CF平分∠ACB交AB于点E.
(1)求∠AEC的度数;
(2)若CD⊥AB于点D,∠CDF=75°.判断△CFD的形状,并说明理由.
参考答案
一.选择题(共5小题,满分25分,每小题5分)
1.解:∵直角三角形的一个锐角等于40°,
∴它的另一个锐角的度数为:90°﹣40°=50°,
选:A.
2.解:A、∵∠A=90°﹣∠C,
∴∠A+∠C=90°,
∴∠B=90°,
∴△ABC是直角三角形,选项不符合题意;
B、∵∠A=∠B﹣∠C,
∴∠A+∠C=∠B,
∵∠A+∠C+∠B=180°,
∴2∠B=180°,
∴∠B=90°,
∴△ABC是直角三角形,选项不符合题意;
C、∵∠A=2∠B=3∠C,
设∠A=x,
∴∠Bx,∠Cx,
∵∠A+∠B+∠C=180°,
∴xxx=180°,
解得x=()°>90°,
∴△ABC不是直角三角形,选项符合题意;
D、∵∠A=∠B∠C,
设∠A=∠B=x,
∴∠C=2x,
∵∠A+∠B+∠C=180°,
∴x+x+2x=180°,
解得x=45°,
∴∠C=2x=90°,
∴△ABC是直角三角形,选项不符合题意.
选:C.
3.解:由勾股定理得,
AC2=AB2+BC2=4+16=20,
∴正方形ADEC的面积为20,
选:C.
4.解:设NB=x,则AN=3﹣x.
由翻折的性质可知:ND=AN=3﹣x.
∵点D是BC的中点,
∴BDBC=1.
在Rt△NBD中,由勾股定理可知:ND2=NB2+DB2,
即(3﹣x)2=x2+12,
∴x,
∴BN,
选:B.
5.解:A、∵22+()2=32,
∴△ABC是直角三角形,不符合题意;
B、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,不符合题意;
C、∵(a+b)2+(a﹣b)2=2c2,
∴a2+b2=c2,
∴△ABC是直角三角形,不符合题意;
D、∵∠A:∠B:∠C=2:3:4,
∴设∠A=2k,则∠B=3k,∠C=4k,
∴2k+3k+4k=180°,解得k=20°,
∴∠C=4k=80°,
∴△ABC不是直角三角形,符合题意.
选:D.
二.填空题(共5小题,满分25分,每小题5分)
6.解:∵△ABC中,∠ACB=90°,∠A=52°,
∴∠B=90°﹣52°=38°,
由题意可知△ECD≌△ACD,
∴∠CED=∠A=52°,
由图可知∠CED是△EBD 的外角,
∴∠CED=∠B+∠EDB,
∴52°=38°+∠EDB,
∴∠EDB=14°.
答案为:14°.
7.解:在直角三角形中,一个锐角为38°,则另一个锐角等于90°﹣38°=52°.
答案为52.
8.解:在△ABC中,∠ACB=90°,∠A=24°,
∴∠B=90°﹣∠A=66°.
由折叠的性质可得:∠BCD∠ACB=45°,∠BDC=∠EDC,
∴∠BDC=180°﹣∠BCD﹣∠B=69°.
∴∠EDC=69°.
答案为:69.
9.解:①同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,是真命题;
②如果三角形的三边长a,b,c(c为最长边)且满足a2+b2=c2,那么这个三角形是直角三角形的逆命题是如果这个三角形是直角三角形,那么三角形的三边长a,b,c(c为最长边)满足a2+b2=c2,是真命题;
③如果两个角是直角,那么它们相等的逆命题是如果两个角相等,那么这两个角是直角,是假命题;
④如果两个实数相等,那么它们的平方相等的逆命题是如果两个实数的平方相等,那么两个实数相等,是假命题;
答案为:①②.
10.解:∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,
∴∠BCD=∠ECD=45°,∠B=∠CED,
∵∠A=25°,
∴∠B=90°﹣25°=65°,
∴∠CED=65°,
∴∠CDE=180°﹣45°﹣65°=70°,
答案为:70°.
三.解答题(共5小题,满分50分,每小题10分)
11.解:设PA=x=PB,可得:CP=5﹣x,
∵根据勾股定理可得:AC2+CP2=PA2,
∴22+(5﹣x)2=x2,
,
∴PA的长为.
12.证明:由图可得,AB5,AC2,BC,
∵52,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
13.解:∵CE⊥AF,
∴∠DEF=90°,
∴∠EDF=90°﹣∠F=90°﹣40°=50°;
由三角形的内角和定理得,∠C+∠DBC=∠F+∠DEF,
所以,30°+∠DBC=40°+90°,
所以,∠DBC=100°.
14.解:△ACD是直角三角形,
理由:∵∠B=90°,BC=1,AB,
∴AC2,
∵CD=2,AD=2,
∴AC2+CD2=22+22=8,AD2=(2)2=8,
∴AC2+CD2=AD2,
∴△ACD是直角三角形.
15.解:(1)∵∠A=30°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=90°,
∵CF平分∠ACB,
∴∠BCE∠ACB=45°,
∵∠AEC是△BCE的外角,
∴∠AEC=∠B+∠BCE=105°;
(2)△CFD是直角三角形,理由如下:
由(1)得:∠BCE=45°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠BCD=180°﹣∠BDC﹣∠B=30°,
∴∠DCF=∠BCE﹣∠BCD=15°,
∵∠CDF=75°,
∴∠CFD=180°﹣∠CDF﹣∠DCF=90°,
∴△CFD是直角三角形.
第4页(共8页)
考试时间:30分钟;总分:100分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共5小题,满分25分,每小题5分)
1.若直角三角形的一个锐角等于40°,则它的另一个锐角等于( )
A.50° B.60° C.70° D.140°
2.在下列条件中不能判定△ABC为直角三角形的是( )
A.∠A=90°﹣∠C B.∠A=∠B﹣∠C
C.∠A=2∠B=3∠C D.∠A=∠B∠C
3.如图,在△ABC中,∠B=90°,AB=2、BC=4,四边形ADEC是正方形,则正方形ADEC的面积是( )
A.8 B.16 C.20 D.25
4.如图,Rt△ABC中,AB=3,BC=2,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A. B. C. D.
5.已知a,b,c是△ABC的三条边,则下列条件不能判定△ABC是直角三角形的是( )
A.a=2,b,c=3 B.∠A+∠B=∠C
C.(a+b)2+(a﹣b)2=2c2 D.∠A:∠B:∠C=2:3:4
二.填空题(共5小题,满分25分,每小题5分)
6.如图,在△ABC中,∠ACB=90°,∠A=52°,将其折叠,使点A落在边BC上的点E处,CA与CE重合,折痕为CD,则∠EDB的度数是 .
7.在直角三角形中,一个锐角为38°,则另一个锐角等于 °.
8.如图,在△ABC中,∠ACB=90°,将三角形纸片ABC沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=24°,则∠EDC= .
9.下列命题中,其逆命题成立的是 (填序号)
①同旁内角互补,两直线平行;
②如果三角形的三边长a,b,c(c为最长边)且满足a2+b2=c2,那么这个三角形是直角三角形.
③如果两个角是直角,那么它们相等;
④如果两个实数相等,那么它们的平方相等;
10.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=25°,则∠CDE= .
三.解答题(共5小题,满分50分,每小题10分)
11.(10分)如图,在Rt△ABC中,∠C=90°.在边BC上有一点P,连接AP,且PA=PB,若AC=2,CB=5,求PA的长.
12.(10分)如图,正方形网格中每个小正方形方格的边长都为1,且点A,B,C均为格点.求证:△ABC是直角三角形.
13.(10分)如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=40°,∠C=30°,求∠EDF、∠DBC的度数.
14.(10分)如图,连接四边形ABCD的对角线AC,已知∠B=90°,BC=1,AB,CD=2,AD=2,请问△ACD是直角三角形吗?请说明你判断的理由.
15.(10分)如图,在△ABC中,∠A=30°,∠B=60°,CF平分∠ACB交AB于点E.
(1)求∠AEC的度数;
(2)若CD⊥AB于点D,∠CDF=75°.判断△CFD的形状,并说明理由.
参考答案
一.选择题(共5小题,满分25分,每小题5分)
1.解:∵直角三角形的一个锐角等于40°,
∴它的另一个锐角的度数为:90°﹣40°=50°,
选:A.
2.解:A、∵∠A=90°﹣∠C,
∴∠A+∠C=90°,
∴∠B=90°,
∴△ABC是直角三角形,选项不符合题意;
B、∵∠A=∠B﹣∠C,
∴∠A+∠C=∠B,
∵∠A+∠C+∠B=180°,
∴2∠B=180°,
∴∠B=90°,
∴△ABC是直角三角形,选项不符合题意;
C、∵∠A=2∠B=3∠C,
设∠A=x,
∴∠Bx,∠Cx,
∵∠A+∠B+∠C=180°,
∴xxx=180°,
解得x=()°>90°,
∴△ABC不是直角三角形,选项符合题意;
D、∵∠A=∠B∠C,
设∠A=∠B=x,
∴∠C=2x,
∵∠A+∠B+∠C=180°,
∴x+x+2x=180°,
解得x=45°,
∴∠C=2x=90°,
∴△ABC是直角三角形,选项不符合题意.
选:C.
3.解:由勾股定理得,
AC2=AB2+BC2=4+16=20,
∴正方形ADEC的面积为20,
选:C.
4.解:设NB=x,则AN=3﹣x.
由翻折的性质可知:ND=AN=3﹣x.
∵点D是BC的中点,
∴BDBC=1.
在Rt△NBD中,由勾股定理可知:ND2=NB2+DB2,
即(3﹣x)2=x2+12,
∴x,
∴BN,
选:B.
5.解:A、∵22+()2=32,
∴△ABC是直角三角形,不符合题意;
B、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,不符合题意;
C、∵(a+b)2+(a﹣b)2=2c2,
∴a2+b2=c2,
∴△ABC是直角三角形,不符合题意;
D、∵∠A:∠B:∠C=2:3:4,
∴设∠A=2k,则∠B=3k,∠C=4k,
∴2k+3k+4k=180°,解得k=20°,
∴∠C=4k=80°,
∴△ABC不是直角三角形,符合题意.
选:D.
二.填空题(共5小题,满分25分,每小题5分)
6.解:∵△ABC中,∠ACB=90°,∠A=52°,
∴∠B=90°﹣52°=38°,
由题意可知△ECD≌△ACD,
∴∠CED=∠A=52°,
由图可知∠CED是△EBD 的外角,
∴∠CED=∠B+∠EDB,
∴52°=38°+∠EDB,
∴∠EDB=14°.
答案为:14°.
7.解:在直角三角形中,一个锐角为38°,则另一个锐角等于90°﹣38°=52°.
答案为52.
8.解:在△ABC中,∠ACB=90°,∠A=24°,
∴∠B=90°﹣∠A=66°.
由折叠的性质可得:∠BCD∠ACB=45°,∠BDC=∠EDC,
∴∠BDC=180°﹣∠BCD﹣∠B=69°.
∴∠EDC=69°.
答案为:69.
9.解:①同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,是真命题;
②如果三角形的三边长a,b,c(c为最长边)且满足a2+b2=c2,那么这个三角形是直角三角形的逆命题是如果这个三角形是直角三角形,那么三角形的三边长a,b,c(c为最长边)满足a2+b2=c2,是真命题;
③如果两个角是直角,那么它们相等的逆命题是如果两个角相等,那么这两个角是直角,是假命题;
④如果两个实数相等,那么它们的平方相等的逆命题是如果两个实数的平方相等,那么两个实数相等,是假命题;
答案为:①②.
10.解:∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,
∴∠BCD=∠ECD=45°,∠B=∠CED,
∵∠A=25°,
∴∠B=90°﹣25°=65°,
∴∠CED=65°,
∴∠CDE=180°﹣45°﹣65°=70°,
答案为:70°.
三.解答题(共5小题,满分50分,每小题10分)
11.解:设PA=x=PB,可得:CP=5﹣x,
∵根据勾股定理可得:AC2+CP2=PA2,
∴22+(5﹣x)2=x2,
,
∴PA的长为.
12.证明:由图可得,AB5,AC2,BC,
∵52,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
13.解:∵CE⊥AF,
∴∠DEF=90°,
∴∠EDF=90°﹣∠F=90°﹣40°=50°;
由三角形的内角和定理得,∠C+∠DBC=∠F+∠DEF,
所以,30°+∠DBC=40°+90°,
所以,∠DBC=100°.
14.解:△ACD是直角三角形,
理由:∵∠B=90°,BC=1,AB,
∴AC2,
∵CD=2,AD=2,
∴AC2+CD2=22+22=8,AD2=(2)2=8,
∴AC2+CD2=AD2,
∴△ACD是直角三角形.
15.解:(1)∵∠A=30°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=90°,
∵CF平分∠ACB,
∴∠BCE∠ACB=45°,
∵∠AEC是△BCE的外角,
∴∠AEC=∠B+∠BCE=105°;
(2)△CFD是直角三角形,理由如下:
由(1)得:∠BCE=45°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠BCD=180°﹣∠BDC﹣∠B=30°,
∴∠DCF=∠BCE﹣∠BCD=15°,
∵∠CDF=75°,
∴∠CFD=180°﹣∠CDF﹣∠DCF=90°,
∴△CFD是直角三角形.
第4页(共8页)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
