山西省朔州市部分学校2024-2025学年下学期开学考九年级数学试卷(PDF版,含答案)
文档属性
| 名称 | 山西省朔州市部分学校2024-2025学年下学期开学考九年级数学试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-18 11:04:57 | ||
图片预览




文档简介
姓名: 准考证号:
机密★启用前
山西 2025 年中考开学模拟
数 学 试 卷
注意事项:
1.本试卷分第Ⅰ卷和第Ⅱ卷两部分.全卷共 6页,满分 120分,考试时间 120分钟.
2.答卷前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置.
3.答案全部在答题卡上完成,答在本试卷上无效.
4.考试结束后,将本试卷和答题卡一并交回.
第Ⅰ卷 选择题(共 30 分)
得 分 评 分 人
一、选择题(本大题共 10 个小题,每小题 3 分,共 30 分.在每个小题给出的四个选项中,只有一
项符合题目要求,请把正确答案的代号填在下表中)
题号 1 2 3 4 5 6 7 8 9 10
答案
1.-5的相反数是
A.-5 B.5 C.15 D.-
1
5
2.下列图案中,不是中心对称图形的是
3.下列计算正确的是
A.a6÷a2=a4B.(a3)2=a5
C.a3+3a3=4a6 D.a3·a3=a9
4.2025年春节档电影爆火,其中最引人注目的是《哪吒 2》,截止 2月 17日下午,其票房达
到了 123.51亿,超越了《狮子王》.数据 123.51亿用科学记数法表示为
A.123.51×108 B.12.351×109
C.1.2351×1011 D.123.51×107
5.在平面直角坐标系中,若点 A(-1,a+b)与点 B(a-b,3)关于 y轴对称,则点 C(-a,b)落在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.若三角形的三边长分别为 a,b,c,且满足 ab-ac=b2-bc,则这个三角形一定是
A.直角三角形 B.等边三角形 C.锐角三角形 D.等腰三角形
7.绿色出行,健康出行,你我同行.某市为了方便市民绿色出行,推出了共享单车服务.图 1是某品
牌共享单车放在水平地面的实物图,图 2是其示意图,其中 AB,CD都与地面平
行,∠BCD=68°,∠BAC=52°.已知 AM与 CB平行,则∠MAC的度数为
A.70° B.68° C.60° D.50°
8.如图,在△ABC中,AB=BC=AC,D是 BC的中点,DE⊥AB于点 E,则△BDE的面积与△ABC的
面积之比为
A.1∶8 B.1∶4 C.1∶2 D.2∶5
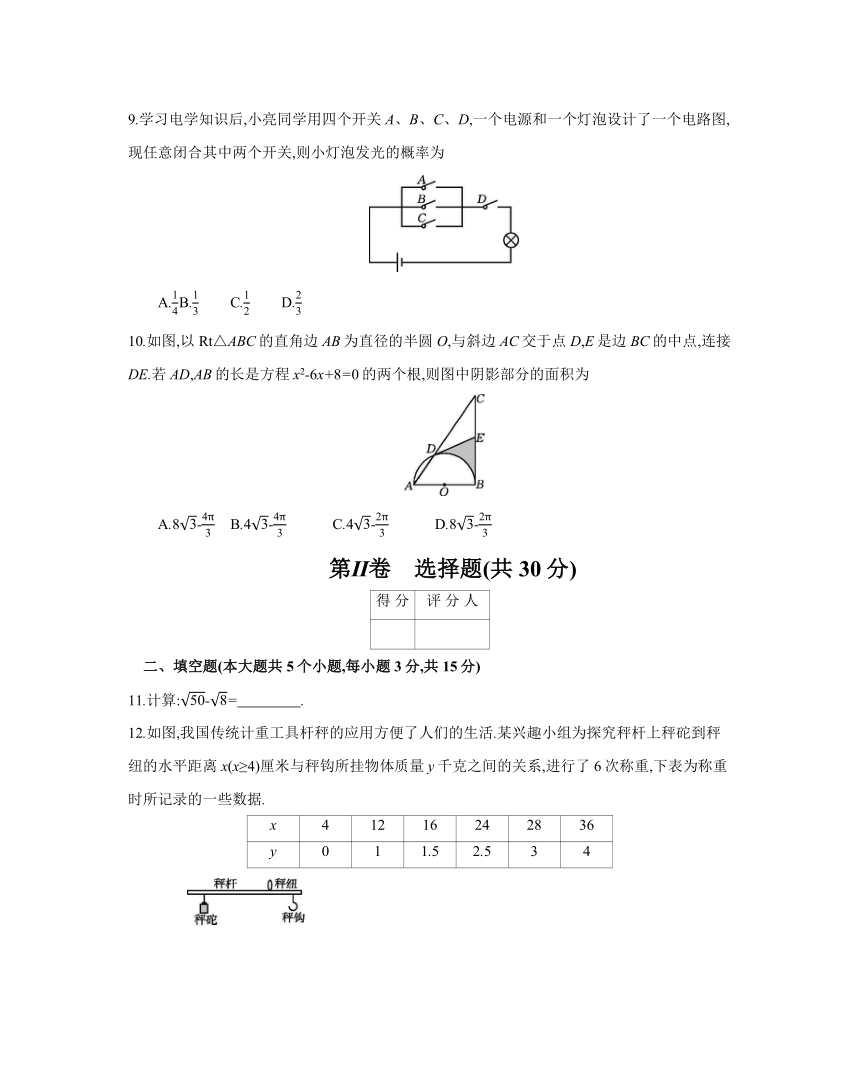
9.学习电学知识后,小亮同学用四个开关 A、B、C、D,一个电源和一个灯泡设计了一个电路图,
现任意闭合其中两个开关,则小灯泡发光的概率为
A.1 1 1 24B.3 C.2 D.3
10.如图,以 Rt△ABC的直角边 AB为直径的半圆 O,与斜边 AC交于点 D,E是边 BC的中点,连接
DE.若 AD,AB的长是方程 x2-6x+8=0的两个根,则图中阴影部分的面积为
A.8 3-4π B.4 3-4π C.4 3-2π D.8 3-2π3 3 3 3
第Ⅱ卷 选择题(共 30 分)
得 分 评 分 人
二、填空题(本大题共 5 个小题,每小题 3 分,共 15 分)
11.计算: 50- 8= .
12.如图,我国传统计重工具杆秤的应用方便了人们的生活.某兴趣小组为探究秤杆上秤砣到秤
纽的水平距离 x(x≥4)厘米与秤钩所挂物体质量 y千克之间的关系,进行了 6次称重,下表为称重
时所记录的一些数据.
x 4 12 16 24 28 36
y 0 1 1.5 2.5 3 4
根据表格中的数据,写出 y关于 x的函数表达式: .
13.我省积极探索保障粮食安全,做强精品粮油,始终坚持“藏粮于地、藏粮于技”战略,稳定粮食
面积,提升基础保障能力,增强科技支撑能力,牢牢把饭碗端在自己手中.某农科所在相同条件下
做某种作物种子发芽率的试验,结果如下表所示:
种子个数 n 1000 1500 2500 4000 8000 15000 20000 30000
发芽种子个数 m 899 1365 2245 3644 7272 13680 18160 27300
m
发芽种子频率n 0.899 0.910 0.898 0.911 0.909 0.912 0.908 0.910
则该作物种子发芽的概率约为 .(结果保留两位小数)
14.将抛物线 y=x2-6x+5先向左平移 2个单位长度,再向上平移 1个单位长度,得到的新抛物线的
顶点坐标为 .
15.如图,在△ABC中,∠ACB=90°,E为 AB的中点,过点 B作 BD⊥AB,交 CE的延长线于点 D.若
BD=4,CD=8,则 AC= .
三、解答题(本大题共 8 个小题,共 75 分.解答应写出文字说明,证明过程或演算步骤)
得 分 评 分 人
16.(本题共 2个小题,每小题 5分,共 10分)
(1)计算:3tan 30°-(12)
-2+| 3-2|.
(2)下面是小明同学化简分式的运算过程,请认真阅读并完成相应任务.
化简:( 2-9-
1
+3)÷
3
3 .
1 3
解:原式=[ - ]÷ .........................................................................................................( +3)( -3) +3 3 第一步
=[ - -3 ]÷ 3 ..............................................................................................................( +3)( -3) ( +3)( -3) 3 第二步
= - +3 ÷ 3 ...............................................................................................................................( +3)( -3) 3 第三步
= 3( +3)( -3)×
3 ...............................................................................................................................
3 第四步
= 1 ............................................................................................................................................... +3 第五步
任务:①以上的运算过程中,第一步是依据 进行变形的;
②第 步开始出现错误,这一步错误的原因是 ;
③请直接写出该分式正确的化简结果.
得 分 评 分 人
17.(本题 8分)
随着 5G网络技术的发展,市场对 5G产品的需求越来越大,为满足市场需求,某大型 5G产品生
产厂家更新技术后,加快了生产速度,现在平均每天比更新技术前多生产 60万件,现在生产 800
万件产品所需时间与更新技术前生产 500万件产品所需时间相同.求更新技术前平均每天生产
产品的件数.
得 分 评 分 人
18.(本题 7分)
如图,在 Rt△ABC中,∠B=90°,BC=2,AB=4.
(1)实践与操作:利用尺规作 AC边上的垂直平分线 DE,垂足为 E,交 AB于点 D(要求:尺规作图并
保留作图痕迹,不写作法,标明字母).
(2)求出线段 DE的长.
得 分 评 分 人
19.(本题 8分)
运动是一切生命的源泉,运动使人健康、使人聪明、使人快乐,运动不仅能改变人的体质,更能
改变人的品格.某初级中学为了解学生一周在家运动时长 t(单位:小时)的情况,从本校学生中随
机抽取了部分学生进行问卷调查,并将收集到的数据整理分析,共分为四组
(A.t<1,B.1≤t<2,C.2≤t<3,D.3≤t<4,其中每周运动时间不少于 3小时为达标),绘制了如下两幅不完
整的统计图.
根据以上信息,解答下列问题:
(1)在这次抽样调查中,共调查了 名学生.
(2)请补全频数分布直方图,并计算在扇形统计图中 C组所对应扇形的圆心角的度数.
(3)若该校有学生 1000人,试估计该校学生一周在家运动时长不足 2小时的人数.
(4)根据调查结果,请对该学校学生每周在家运动情况作出评价,并提出一条合理化的建议.
得 分 评 分 人
20.(本题 8分)阅读与思考
下面是小牛同学的部分日记,请仔细阅读并完成相应的任务:
二次函数的应用
×年×月×日
今天在数学活动学习过程中遇到一个问题:下列两个两位数相乘的运算中(两个乘数的十位上的数都是 2,个位
上的数的和等于 10),21×29,22×28,23×27,…,27×23,28×22,29×21.
请你先猜想,积最大的是 × ,并说明理由.
猜想:积最大的是 25×25.
理由如下:
设两个乘数的积为 y,其中一个乘数的个位上的数为 x,则另一个乘数个位上的数为(10-x).
根据题意得 y=(20+x)[20+(10-x)]=(20+x)(30-x)=-(x+20)(x-30),…
任务:
(1)上面日记中的分析过程中主要运用的数学思想是 .
A.数形结合 B.统计思想 C.分类讨论 D.函数思想
(2)请补全小牛的日记中的解题过程.
(3)下列两个三位数相乘的运算中(两个乘数的百位上的数都是 8,十位上的数与个位上的数组成
的数的和等于 100),801×899,802×898,803×897,…,897×803,898×802,899×801.用以上方法猜想
其中哪个积最大,并说明理由.
得 分 评 分 人
21.(本题 8分)
如图 1,一个纸筒被安装在竖直的墙面上,图 2是其侧面示意图,其中
AB⊥BC,AB∥CE∥DF,AD∥EF∥BC,纸筒盖 CMP可以绕着点 C旋转,关闭时点 P与点 F重
合,CM⊥PM,AB=30 cm,DF=6 cm,CM=EF=7 cm.
(1)若∠BCM=150°,求纸筒盖关闭时点 P运动的路径长.
(2)纸筒盖处于关闭状态,当一卷底面直径为 10 cm的圆柱形纸巾能放入纸筒内时,问纸筒盖
CMP绕点 C至少要旋转多少度 (结果保留整数,参考数据:sin 11.5°≈0.20,cos 11.5°≈0.98,tan
11.5°≈0.20)
得 分 评 分 人
22.(本题 13分)综合与实践
【情境再现】
(1)如图 1,在等腰△ABC中,∠BAC=90°,O为 BC边的中点,有一个内角为 45°的直角三角尺,直
角顶点恰好落在边 BC的中点处,连接 AG,BH,AB交 HO于点 E,AC交 OG于点 F,则 BH与 AG
的位置关系是 ,数量关系是 .
【类比拓展】
(2)如图 2,将图中的△ABC,△OHG换成含 30°角的直角三角形,AO⊥BC,连接 HB,AG,则 BH与
AG的位置和数量关系如何 请证明.
【迁移应用】
(3)在问题(2)中,若 OA=4,BH=4 3,HG=10,则四边形 ABOG的周长为 .
得 分 评 分 人
23.(本题 13分)综合与探究
如图,在平面直角坐标系中,二次函数 y=mx2+nx+4(m≠0)的图象交 x轴于 A,B两点,交 y轴于点 C,
点 A的坐标为(-3,0),点 B的坐标为(1,0),以 OA,OC为边作矩形 OADC,且边 CD交二次函数的图
象于点 M.
(1)求二次函数的表达式.
(2)现有一条垂直于 x轴的直线 x=a在 A,O两点间(不包括 A,O两点)左右移动,分别交 x轴于点
E,交 CD于点 F,交 AC于点 P,交二次函数的图象于点 Q,请用含 a的代数式表示 QP的长.
(3)在(2)的条件下,连接 QC,则在 CD上方的二次函数的图象上是否存在这样的点 Q,使得以
Q,C,F为顶点的三角形和△AEP相似 若存在,直接写出 a的值;若不存在,请说明理由.
数学试卷参考答案
1.B 2.D 3.A 4.B 5.B 6.D 7.C 8.A 9.C
10.B 提示:如图,连接 OD,BD,OE.
∵AB是直径,∴∠ADB=90°.
∵AD,AB的长是方程 x2-6x+8=0的两个根,解得 x1=2,x2=4,
∴AD=2,AB=4,
∴∠ABD=30°,∠BAC=60°.
∵AO=DO,
∴∠AOD=60°,
∴∠BOD=120°,
S =120π·2
2 4π
∴ 扇形BOD 360 = 3 .
∵∠ABC=90°,∠BAC=60°,
∴∠ACB=30°.
在 Rt△ADB中,由勾股定理得 BD= 2-A 2=2 3,
∴BC=4 3,CD=6.
∵E是 BC的中点,
∴DE=BE=BD=2 3,
∴△ODE≌△OBE,
∴S 阴影=S 四边形 BODE-S 扇形 BOD=2S△OBE-S 扇形 BOD
=2×12×2×2 3-
4π
3
=4 3-4π3 .
11.3 2 12.y=18x-
1
2 13.0.91 14.(1,-3)
15.6 55 提示:如图,过点 C作 CF⊥AB于点 F.
设 CE=x,则 DE=CD-CE=8-x.
在 Rt△ABC中,E是 AB的中点,
∴AE=BE=CE=x.
∵BD⊥AB,
∴∠EBD=90°,
∴BE2+BD2=DE2,即 x2+42=(8-x)2,
解得 x=3,
∴AE=BE=CE=3,DE=8-3=5.
∵CF⊥AB,BD⊥AB,
∴∠CFE=∠CFA=∠DBE=90°.
又∵∠CEF=∠DEB,
∴△CFE∽△DBE,
= ∴ =
,
3= = 即5 3 4 ,
9 12
解得 EF=5,CF= 5 ,
∴AF=AE-EF=65.
∵∠CFA=90°,
∴AC= 2 + C 2=6 55 .
16.(1)解:原式=3× 3-4+2- 3............................................................................................................3 3分
= 3-4+2- 3.......................................................................................................................................4分
=-2...................................................................................................................................................... 5分
(2)解:①因式分解.............................................................................................................................. 6分
②五;在约分的过程中符号没有改变...............................................................................................8分
③- 1 ................................................................................................................................................ +3 10分
17.解:设更新技术前每天生产 x万件产品,则更新技术后每天生产(x+60)万件产品................. 1分
, 500= 800根据题意 得 ,........................................................................................................................ +60 4分
解得 x=100,........................................................................................................................................6分
经检验,x=100是原分式方程的解且符合实际,
答:更新技术前每天生产 100万件产品...........................................................................................8分
18.解:(1)如图,直线 DE为所求.........................................................................................................2分
(2)∵∠A=∠A,∠AED=∠ABC=90°,
∴△ADE∽△ACB.............................................................................................................................3分
在 Rt△ABC中,由勾股定理得 AC= 2 + B 2=2 5,
AE=1∴ AC= 5..................................................................................................................................2 4分
∵△ADE∽△ACB,
= , 5∴ 即 = ,............................................................................................................................. 2 4 5分
解得 DE= 5,.......................................................................................................................................2 6分
∴线段 DE 5的长为 .........................................................................................................................2 7分
19.解:(1)120....................................................................................................................................... 1分
提示:被调查的人数为 36÷30%=120.
(2)C组的人数为 120-6-36-30=48,
补全频数分布直方图如图所示:
48
扇形统计图中 C组所对应扇形的圆心角的度数为 360°× =144°............................................120 4分
(3)1000×6+36120=350(名).
答:估计该校学生一周在家运动时长不足 2小时的人数为 350................................................... 6分
(4)该校大部分学生每周在家运动的时间没有达标,建议鼓励学生加强在家运动的时间,做到劳
逸结合,强身健体,做一个德智体美劳全面发展的好少年............................................................. 8分
20.解:(1)D.......................................................................................................................................... 2分
(2)整理得 y=-(x-5)2+625,
∴当 x=5时,y的值最大,y 最大值=625,
∴积最大的是 25×25,最大积为 625................................................................................................4分
(3)850×850.........................................................................................................................................5分
理由:设两个乘数的积为 w,其中一个乘数的十位上的数与个位上的数组成的数为 a,则另一个乘
数的十位上的数与个位上的数组成的数为(100-a),
由题意得 w=(800+a)[800+(100-a)]=-(a-50)2+722500,
∴当 a=50时,w的值最大,最大值为 722500,
∴当 a=50时,850×850的积最大.....................................................................................................8分
21.解:(1)∵AB⊥BC,AB∥CE∥DF,AD∥EF∥BC,
AB=30 cm,AD=18 cm,DF=6 cm,CM=EF=7 cm,
∴CE=30-6=24 cm............................................................................................................................ 2分
如图 1,连接 PC,由勾股定理,得 CP= 72 + 242=25.
∵∠BCM=150°,
∴纸筒盖关闭时需绕着点 C逆时针旋转 30°,
P 30×π×25 25π∴点 运动的路径长为 .........................................................................................180 = 6 cm. 4分
(2)如图 2,连接 OC,CF,CP,PF.
当 PF=10 cm时,圆柱形纸巾恰好能放入纸筒内.
∵CF=CP=25 cm,OF=OP=5 cm,
∴∠OCF=∠OCP,CO⊥FP,
∴sin OCP= = 5=1∠ ....................................................................................................................... 25 5 6分
sin 11.5°≈1∵ 5,
∴∠OCP≈11.5°,
∴∠PCF=2∠OCP≈23°,
∴纸筒盖 CMP绕点 C至少要旋转 23°.......................................................................................... 8分
22.解:(1)BH⊥AG;BH=AG................................................................................................................2分
(2)BH⊥AG;BH= 3AG..................................................................................................................... 4分
证明:在 Rt△AOB中,tan 30°= 3 = 3 ,
在 Rt△HOG中,tan 30°= =
3
3 ,
= ∴ ............................................................................................................................................. 5分
∵AO⊥BC,∠HOG=90°,
∴∠AOB=∠HOG=90°,
∴∠BOH=∠AOG,
∴△BOH∽△AOG,.......................................................................................................................... 7分
∴ =
=
3
3 ,
∴BH= 3AG...................................................................................................................................... 8分
如图,延长 GA交 BH于点 E,与 OH交于点 F.
由△BOH∽△AOG可知,∠OGA=∠OHB.
∵∠HFE=∠GFO,
∴∠HEF=∠GOF=90°,
∴BH⊥AG....................................................................................................................................... 10分
(3)17+4 3........................................................................................................................................ 13分
提示:由题意可知 OG=HG·sin 30°=10×12=5,AB=
sin30°=4×2=8,OB=
3
tan30°=4 ,由(2)知
BH= 3AG=4 3,∴AG=4,
∴四边形 ABOG的周长=8+4+5+4 3=17+4 3.
23.解:(1)∵抛物线 y=mx2+nx+4(m≠0)经过点 A(-3,0),B(1,0).
9 -3 + 4 = 0,
∴ + + 4 = 0, ..............................................................................................................................1分
= 4 ,
解得 3 ....................................................................................................................................3分
= 8
3 ,
4
∴二次函数的表达式为 y=- x2-8x+4...............................................................................................3 3 4分
(2) 4 8由二次函数的表达式为 y=- x2- x+4,得 C(0,4)..........................................................................3 3 5分
设直线 AC的表达式为 y=kx+b.
∵A(-3,0),C(0,4),
0 = 3 + ,
∴ 4 = ,
= 4
解得 3
,
= 4,
∴直线 AC y=4的表达式为 x+4.......................................................................................................3 7分
∵直线 x=a交 AC于点 P,
∴点 P 4的坐标为(a,3a+4).
∵点 Q的横坐标为 a,点 Q在抛物线上,
Q (a,-4 8∴点 的坐标为 23a -3a+4),
∴QP=QE-PE=(-43a
2-8 4 4 23a+4)-(3a+4)=-3a -4a,
QP=-4即 a2-4a(-3(3)a的值为-23或-1...........................................................................................................................16 13分
提示:由题意可得 AE=a+3,EP=43a+4,CF=-a.
QF=-4a2-8a+4-4=-4a2-83 3 3 3a.
若以 Q,C,F为顶点的三角形和△AEP相似,分两种情况:
4 8
: QFC AEP,
- 2-
情况① 若△ ∽△ 则 = ,即 3 3
a
= - +3 4 ,
3a+4
23
解得 a1=-16,a2=-3(舍去).
4 8
: CFQ AEP, =
- 2- a
情况② 若△ ∽△ 则 ,
-
即 3 3 +3= 4 ,
3a+4
解得 a1=-1,a2=-3(舍去).
综上所述,存在这样的点 Q使以 Q,C,F为顶点的三角形和△AEP相似, a -23此时 的值为 16或-1.
机密★启用前
山西 2025 年中考开学模拟
数 学 试 卷
注意事项:
1.本试卷分第Ⅰ卷和第Ⅱ卷两部分.全卷共 6页,满分 120分,考试时间 120分钟.
2.答卷前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置.
3.答案全部在答题卡上完成,答在本试卷上无效.
4.考试结束后,将本试卷和答题卡一并交回.
第Ⅰ卷 选择题(共 30 分)
得 分 评 分 人
一、选择题(本大题共 10 个小题,每小题 3 分,共 30 分.在每个小题给出的四个选项中,只有一
项符合题目要求,请把正确答案的代号填在下表中)
题号 1 2 3 4 5 6 7 8 9 10
答案
1.-5的相反数是
A.-5 B.5 C.15 D.-
1
5
2.下列图案中,不是中心对称图形的是
3.下列计算正确的是
A.a6÷a2=a4B.(a3)2=a5
C.a3+3a3=4a6 D.a3·a3=a9
4.2025年春节档电影爆火,其中最引人注目的是《哪吒 2》,截止 2月 17日下午,其票房达
到了 123.51亿,超越了《狮子王》.数据 123.51亿用科学记数法表示为
A.123.51×108 B.12.351×109
C.1.2351×1011 D.123.51×107
5.在平面直角坐标系中,若点 A(-1,a+b)与点 B(a-b,3)关于 y轴对称,则点 C(-a,b)落在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.若三角形的三边长分别为 a,b,c,且满足 ab-ac=b2-bc,则这个三角形一定是
A.直角三角形 B.等边三角形 C.锐角三角形 D.等腰三角形
7.绿色出行,健康出行,你我同行.某市为了方便市民绿色出行,推出了共享单车服务.图 1是某品
牌共享单车放在水平地面的实物图,图 2是其示意图,其中 AB,CD都与地面平
行,∠BCD=68°,∠BAC=52°.已知 AM与 CB平行,则∠MAC的度数为
A.70° B.68° C.60° D.50°
8.如图,在△ABC中,AB=BC=AC,D是 BC的中点,DE⊥AB于点 E,则△BDE的面积与△ABC的
面积之比为
A.1∶8 B.1∶4 C.1∶2 D.2∶5
9.学习电学知识后,小亮同学用四个开关 A、B、C、D,一个电源和一个灯泡设计了一个电路图,
现任意闭合其中两个开关,则小灯泡发光的概率为
A.1 1 1 24B.3 C.2 D.3
10.如图,以 Rt△ABC的直角边 AB为直径的半圆 O,与斜边 AC交于点 D,E是边 BC的中点,连接
DE.若 AD,AB的长是方程 x2-6x+8=0的两个根,则图中阴影部分的面积为
A.8 3-4π B.4 3-4π C.4 3-2π D.8 3-2π3 3 3 3
第Ⅱ卷 选择题(共 30 分)
得 分 评 分 人
二、填空题(本大题共 5 个小题,每小题 3 分,共 15 分)
11.计算: 50- 8= .
12.如图,我国传统计重工具杆秤的应用方便了人们的生活.某兴趣小组为探究秤杆上秤砣到秤
纽的水平距离 x(x≥4)厘米与秤钩所挂物体质量 y千克之间的关系,进行了 6次称重,下表为称重
时所记录的一些数据.
x 4 12 16 24 28 36
y 0 1 1.5 2.5 3 4
根据表格中的数据,写出 y关于 x的函数表达式: .
13.我省积极探索保障粮食安全,做强精品粮油,始终坚持“藏粮于地、藏粮于技”战略,稳定粮食
面积,提升基础保障能力,增强科技支撑能力,牢牢把饭碗端在自己手中.某农科所在相同条件下
做某种作物种子发芽率的试验,结果如下表所示:
种子个数 n 1000 1500 2500 4000 8000 15000 20000 30000
发芽种子个数 m 899 1365 2245 3644 7272 13680 18160 27300
m
发芽种子频率n 0.899 0.910 0.898 0.911 0.909 0.912 0.908 0.910
则该作物种子发芽的概率约为 .(结果保留两位小数)
14.将抛物线 y=x2-6x+5先向左平移 2个单位长度,再向上平移 1个单位长度,得到的新抛物线的
顶点坐标为 .
15.如图,在△ABC中,∠ACB=90°,E为 AB的中点,过点 B作 BD⊥AB,交 CE的延长线于点 D.若
BD=4,CD=8,则 AC= .
三、解答题(本大题共 8 个小题,共 75 分.解答应写出文字说明,证明过程或演算步骤)
得 分 评 分 人
16.(本题共 2个小题,每小题 5分,共 10分)
(1)计算:3tan 30°-(12)
-2+| 3-2|.
(2)下面是小明同学化简分式的运算过程,请认真阅读并完成相应任务.
化简:( 2-9-
1
+3)÷
3
3 .
1 3
解:原式=[ - ]÷ .........................................................................................................( +3)( -3) +3 3 第一步
=[ - -3 ]÷ 3 ..............................................................................................................( +3)( -3) ( +3)( -3) 3 第二步
= - +3 ÷ 3 ...............................................................................................................................( +3)( -3) 3 第三步
= 3( +3)( -3)×
3 ...............................................................................................................................
3 第四步
= 1 ............................................................................................................................................... +3 第五步
任务:①以上的运算过程中,第一步是依据 进行变形的;
②第 步开始出现错误,这一步错误的原因是 ;
③请直接写出该分式正确的化简结果.
得 分 评 分 人
17.(本题 8分)
随着 5G网络技术的发展,市场对 5G产品的需求越来越大,为满足市场需求,某大型 5G产品生
产厂家更新技术后,加快了生产速度,现在平均每天比更新技术前多生产 60万件,现在生产 800
万件产品所需时间与更新技术前生产 500万件产品所需时间相同.求更新技术前平均每天生产
产品的件数.
得 分 评 分 人
18.(本题 7分)
如图,在 Rt△ABC中,∠B=90°,BC=2,AB=4.
(1)实践与操作:利用尺规作 AC边上的垂直平分线 DE,垂足为 E,交 AB于点 D(要求:尺规作图并
保留作图痕迹,不写作法,标明字母).
(2)求出线段 DE的长.
得 分 评 分 人
19.(本题 8分)
运动是一切生命的源泉,运动使人健康、使人聪明、使人快乐,运动不仅能改变人的体质,更能
改变人的品格.某初级中学为了解学生一周在家运动时长 t(单位:小时)的情况,从本校学生中随
机抽取了部分学生进行问卷调查,并将收集到的数据整理分析,共分为四组
(A.t<1,B.1≤t<2,C.2≤t<3,D.3≤t<4,其中每周运动时间不少于 3小时为达标),绘制了如下两幅不完
整的统计图.
根据以上信息,解答下列问题:
(1)在这次抽样调查中,共调查了 名学生.
(2)请补全频数分布直方图,并计算在扇形统计图中 C组所对应扇形的圆心角的度数.
(3)若该校有学生 1000人,试估计该校学生一周在家运动时长不足 2小时的人数.
(4)根据调查结果,请对该学校学生每周在家运动情况作出评价,并提出一条合理化的建议.
得 分 评 分 人
20.(本题 8分)阅读与思考
下面是小牛同学的部分日记,请仔细阅读并完成相应的任务:
二次函数的应用
×年×月×日
今天在数学活动学习过程中遇到一个问题:下列两个两位数相乘的运算中(两个乘数的十位上的数都是 2,个位
上的数的和等于 10),21×29,22×28,23×27,…,27×23,28×22,29×21.
请你先猜想,积最大的是 × ,并说明理由.
猜想:积最大的是 25×25.
理由如下:
设两个乘数的积为 y,其中一个乘数的个位上的数为 x,则另一个乘数个位上的数为(10-x).
根据题意得 y=(20+x)[20+(10-x)]=(20+x)(30-x)=-(x+20)(x-30),…
任务:
(1)上面日记中的分析过程中主要运用的数学思想是 .
A.数形结合 B.统计思想 C.分类讨论 D.函数思想
(2)请补全小牛的日记中的解题过程.
(3)下列两个三位数相乘的运算中(两个乘数的百位上的数都是 8,十位上的数与个位上的数组成
的数的和等于 100),801×899,802×898,803×897,…,897×803,898×802,899×801.用以上方法猜想
其中哪个积最大,并说明理由.
得 分 评 分 人
21.(本题 8分)
如图 1,一个纸筒被安装在竖直的墙面上,图 2是其侧面示意图,其中
AB⊥BC,AB∥CE∥DF,AD∥EF∥BC,纸筒盖 CMP可以绕着点 C旋转,关闭时点 P与点 F重
合,CM⊥PM,AB=30 cm,DF=6 cm,CM=EF=7 cm.
(1)若∠BCM=150°,求纸筒盖关闭时点 P运动的路径长.
(2)纸筒盖处于关闭状态,当一卷底面直径为 10 cm的圆柱形纸巾能放入纸筒内时,问纸筒盖
CMP绕点 C至少要旋转多少度 (结果保留整数,参考数据:sin 11.5°≈0.20,cos 11.5°≈0.98,tan
11.5°≈0.20)
得 分 评 分 人
22.(本题 13分)综合与实践
【情境再现】
(1)如图 1,在等腰△ABC中,∠BAC=90°,O为 BC边的中点,有一个内角为 45°的直角三角尺,直
角顶点恰好落在边 BC的中点处,连接 AG,BH,AB交 HO于点 E,AC交 OG于点 F,则 BH与 AG
的位置关系是 ,数量关系是 .
【类比拓展】
(2)如图 2,将图中的△ABC,△OHG换成含 30°角的直角三角形,AO⊥BC,连接 HB,AG,则 BH与
AG的位置和数量关系如何 请证明.
【迁移应用】
(3)在问题(2)中,若 OA=4,BH=4 3,HG=10,则四边形 ABOG的周长为 .
得 分 评 分 人
23.(本题 13分)综合与探究
如图,在平面直角坐标系中,二次函数 y=mx2+nx+4(m≠0)的图象交 x轴于 A,B两点,交 y轴于点 C,
点 A的坐标为(-3,0),点 B的坐标为(1,0),以 OA,OC为边作矩形 OADC,且边 CD交二次函数的图
象于点 M.
(1)求二次函数的表达式.
(2)现有一条垂直于 x轴的直线 x=a在 A,O两点间(不包括 A,O两点)左右移动,分别交 x轴于点
E,交 CD于点 F,交 AC于点 P,交二次函数的图象于点 Q,请用含 a的代数式表示 QP的长.
(3)在(2)的条件下,连接 QC,则在 CD上方的二次函数的图象上是否存在这样的点 Q,使得以
Q,C,F为顶点的三角形和△AEP相似 若存在,直接写出 a的值;若不存在,请说明理由.
数学试卷参考答案
1.B 2.D 3.A 4.B 5.B 6.D 7.C 8.A 9.C
10.B 提示:如图,连接 OD,BD,OE.
∵AB是直径,∴∠ADB=90°.
∵AD,AB的长是方程 x2-6x+8=0的两个根,解得 x1=2,x2=4,
∴AD=2,AB=4,
∴∠ABD=30°,∠BAC=60°.
∵AO=DO,
∴∠AOD=60°,
∴∠BOD=120°,
S =120π·2
2 4π
∴ 扇形BOD 360 = 3 .
∵∠ABC=90°,∠BAC=60°,
∴∠ACB=30°.
在 Rt△ADB中,由勾股定理得 BD= 2-A 2=2 3,
∴BC=4 3,CD=6.
∵E是 BC的中点,
∴DE=BE=BD=2 3,
∴△ODE≌△OBE,
∴S 阴影=S 四边形 BODE-S 扇形 BOD=2S△OBE-S 扇形 BOD
=2×12×2×2 3-
4π
3
=4 3-4π3 .
11.3 2 12.y=18x-
1
2 13.0.91 14.(1,-3)
15.6 55 提示:如图,过点 C作 CF⊥AB于点 F.
设 CE=x,则 DE=CD-CE=8-x.
在 Rt△ABC中,E是 AB的中点,
∴AE=BE=CE=x.
∵BD⊥AB,
∴∠EBD=90°,
∴BE2+BD2=DE2,即 x2+42=(8-x)2,
解得 x=3,
∴AE=BE=CE=3,DE=8-3=5.
∵CF⊥AB,BD⊥AB,
∴∠CFE=∠CFA=∠DBE=90°.
又∵∠CEF=∠DEB,
∴△CFE∽△DBE,
= ∴ =
,
3= = 即5 3 4 ,
9 12
解得 EF=5,CF= 5 ,
∴AF=AE-EF=65.
∵∠CFA=90°,
∴AC= 2 + C 2=6 55 .
16.(1)解:原式=3× 3-4+2- 3............................................................................................................3 3分
= 3-4+2- 3.......................................................................................................................................4分
=-2...................................................................................................................................................... 5分
(2)解:①因式分解.............................................................................................................................. 6分
②五;在约分的过程中符号没有改变...............................................................................................8分
③- 1 ................................................................................................................................................ +3 10分
17.解:设更新技术前每天生产 x万件产品,则更新技术后每天生产(x+60)万件产品................. 1分
, 500= 800根据题意 得 ,........................................................................................................................ +60 4分
解得 x=100,........................................................................................................................................6分
经检验,x=100是原分式方程的解且符合实际,
答:更新技术前每天生产 100万件产品...........................................................................................8分
18.解:(1)如图,直线 DE为所求.........................................................................................................2分
(2)∵∠A=∠A,∠AED=∠ABC=90°,
∴△ADE∽△ACB.............................................................................................................................3分
在 Rt△ABC中,由勾股定理得 AC= 2 + B 2=2 5,
AE=1∴ AC= 5..................................................................................................................................2 4分
∵△ADE∽△ACB,
= , 5∴ 即 = ,............................................................................................................................. 2 4 5分
解得 DE= 5,.......................................................................................................................................2 6分
∴线段 DE 5的长为 .........................................................................................................................2 7分
19.解:(1)120....................................................................................................................................... 1分
提示:被调查的人数为 36÷30%=120.
(2)C组的人数为 120-6-36-30=48,
补全频数分布直方图如图所示:
48
扇形统计图中 C组所对应扇形的圆心角的度数为 360°× =144°............................................120 4分
(3)1000×6+36120=350(名).
答:估计该校学生一周在家运动时长不足 2小时的人数为 350................................................... 6分
(4)该校大部分学生每周在家运动的时间没有达标,建议鼓励学生加强在家运动的时间,做到劳
逸结合,强身健体,做一个德智体美劳全面发展的好少年............................................................. 8分
20.解:(1)D.......................................................................................................................................... 2分
(2)整理得 y=-(x-5)2+625,
∴当 x=5时,y的值最大,y 最大值=625,
∴积最大的是 25×25,最大积为 625................................................................................................4分
(3)850×850.........................................................................................................................................5分
理由:设两个乘数的积为 w,其中一个乘数的十位上的数与个位上的数组成的数为 a,则另一个乘
数的十位上的数与个位上的数组成的数为(100-a),
由题意得 w=(800+a)[800+(100-a)]=-(a-50)2+722500,
∴当 a=50时,w的值最大,最大值为 722500,
∴当 a=50时,850×850的积最大.....................................................................................................8分
21.解:(1)∵AB⊥BC,AB∥CE∥DF,AD∥EF∥BC,
AB=30 cm,AD=18 cm,DF=6 cm,CM=EF=7 cm,
∴CE=30-6=24 cm............................................................................................................................ 2分
如图 1,连接 PC,由勾股定理,得 CP= 72 + 242=25.
∵∠BCM=150°,
∴纸筒盖关闭时需绕着点 C逆时针旋转 30°,
P 30×π×25 25π∴点 运动的路径长为 .........................................................................................180 = 6 cm. 4分
(2)如图 2,连接 OC,CF,CP,PF.
当 PF=10 cm时,圆柱形纸巾恰好能放入纸筒内.
∵CF=CP=25 cm,OF=OP=5 cm,
∴∠OCF=∠OCP,CO⊥FP,
∴sin OCP= = 5=1∠ ....................................................................................................................... 25 5 6分
sin 11.5°≈1∵ 5,
∴∠OCP≈11.5°,
∴∠PCF=2∠OCP≈23°,
∴纸筒盖 CMP绕点 C至少要旋转 23°.......................................................................................... 8分
22.解:(1)BH⊥AG;BH=AG................................................................................................................2分
(2)BH⊥AG;BH= 3AG..................................................................................................................... 4分
证明:在 Rt△AOB中,tan 30°= 3 = 3 ,
在 Rt△HOG中,tan 30°= =
3
3 ,
= ∴ ............................................................................................................................................. 5分
∵AO⊥BC,∠HOG=90°,
∴∠AOB=∠HOG=90°,
∴∠BOH=∠AOG,
∴△BOH∽△AOG,.......................................................................................................................... 7分
∴ =
=
3
3 ,
∴BH= 3AG...................................................................................................................................... 8分
如图,延长 GA交 BH于点 E,与 OH交于点 F.
由△BOH∽△AOG可知,∠OGA=∠OHB.
∵∠HFE=∠GFO,
∴∠HEF=∠GOF=90°,
∴BH⊥AG....................................................................................................................................... 10分
(3)17+4 3........................................................................................................................................ 13分
提示:由题意可知 OG=HG·sin 30°=10×12=5,AB=
sin30°=4×2=8,OB=
3
tan30°=4 ,由(2)知
BH= 3AG=4 3,∴AG=4,
∴四边形 ABOG的周长=8+4+5+4 3=17+4 3.
23.解:(1)∵抛物线 y=mx2+nx+4(m≠0)经过点 A(-3,0),B(1,0).
9 -3 + 4 = 0,
∴ + + 4 = 0, ..............................................................................................................................1分
= 4 ,
解得 3 ....................................................................................................................................3分
= 8
3 ,
4
∴二次函数的表达式为 y=- x2-8x+4...............................................................................................3 3 4分
(2) 4 8由二次函数的表达式为 y=- x2- x+4,得 C(0,4)..........................................................................3 3 5分
设直线 AC的表达式为 y=kx+b.
∵A(-3,0),C(0,4),
0 = 3 + ,
∴ 4 = ,
= 4
解得 3
,
= 4,
∴直线 AC y=4的表达式为 x+4.......................................................................................................3 7分
∵直线 x=a交 AC于点 P,
∴点 P 4的坐标为(a,3a+4).
∵点 Q的横坐标为 a,点 Q在抛物线上,
Q (a,-4 8∴点 的坐标为 23a -3a+4),
∴QP=QE-PE=(-43a
2-8 4 4 23a+4)-(3a+4)=-3a -4a,
QP=-4即 a2-4a(-3
提示:由题意可得 AE=a+3,EP=43a+4,CF=-a.
QF=-4a2-8a+4-4=-4a2-83 3 3 3a.
若以 Q,C,F为顶点的三角形和△AEP相似,分两种情况:
4 8
: QFC AEP,
- 2-
情况① 若△ ∽△ 则 = ,即 3 3
a
= - +3 4 ,
3a+4
23
解得 a1=-16,a2=-3(舍去).
4 8
: CFQ AEP, =
- 2- a
情况② 若△ ∽△ 则 ,
-
即 3 3 +3= 4 ,
3a+4
解得 a1=-1,a2=-3(舍去).
综上所述,存在这样的点 Q使以 Q,C,F为顶点的三角形和△AEP相似, a -23此时 的值为 16或-1.
同课章节目录
