2024-2025学年北师大版七年级数学下册课件 1.1 幂的乘除( 课时1)——同底数幂的乘法(29张PPT)
文档属性
| 名称 | 2024-2025学年北师大版七年级数学下册课件 1.1 幂的乘除( 课时1)——同底数幂的乘法(29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 602.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-18 10:46:57 | ||
图片预览








文档简介
(共29张PPT)
北师大版七年级数学下册课件
第一章 整式的乘除
1.1幂的乘除
课时1——同底数幂的乘法
1.了解幂的乘方的运算法则,熟练运用幂的乘方的运算法则进行实际计算.(重点)
2.掌握幂的乘方的运算法则的推导.(难点)
3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.
学习目标
新课导入
(1) (x2)2 = x2 2= x4 ;
(2) (x2)3 = x2 3= x6 .
观察计算结果,你能发现什么规律?
(1) (x2)2 = x2 x2 = x2+2= x4 ;
(2) (x2)3 = x2 x2 x2 = x2+2+2= x6 .
结 论
新课导入
观察计算结果,你能发现什么规律?(m,n为正整数)
(1) (32)3=32×32×32=36 ;
(2) (a2)3=a2×a2×a2=a6 ;
(3) (am)3=am×am×am=a3m (m是正整数);
(4) (am)n=am×am× am=amn (m,n为正整数).
n个am
新课导入
规 律
以上式子都是幂的乘方的形式,根据已经学过的乘方的意义和同底数幂的乘法性质可以得出幂的乘方的结果中底数不变,指数为两个指数的乘积(其中指数均为正整数).
思考:你能总结出幂的乘方的运算法则吗
新课讲解
知识点1 幂的乘方
性质:幂的乘方,底数不变,指数相乘.
n个m
n个am
符号表示:(am)n=amn(m,n都是正整数).
一般地,对于任意底数a与任意正整数m,n.
(am)n=am×am× am=amn
=a(m+m+m+ +m)
新课讲解
知识点1 幂的乘方
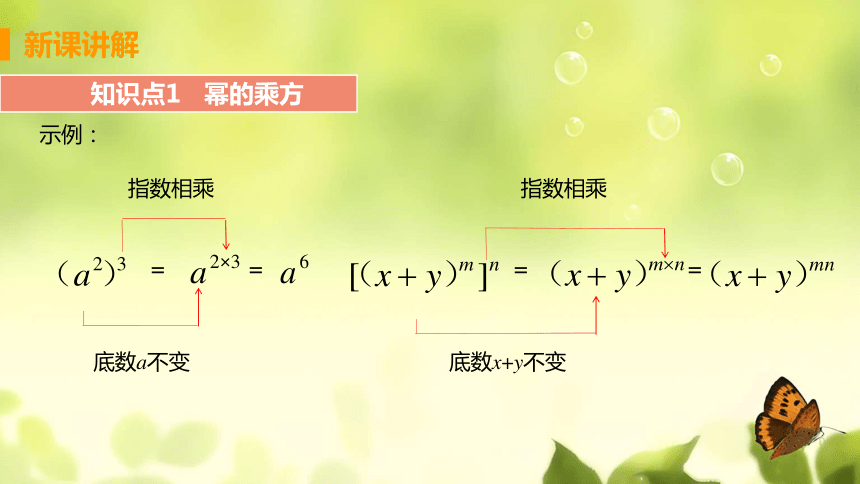
示例:
= = = =
底数a不变
指数相乘
底数x+y不变
指数相乘
新课讲解
(1) 幂的乘方的性质也可以推广为 [(am)n]p=amnp
(m,n,p都为正整数).
(2) 幂的乘方的性质可以逆用,即 amn=(am)n (m,n为正整数).
知识点1 幂的乘方
新课讲解
(1)在形式上,幂的乘方的底数本身就是一个幂,根据乘方的意义和同底数幂的乘法的性质可以推出幂的乘方的性质;
(2)在幂的乘方中,底数可以是单项式,也可以是多项式.
幂的乘方用性质,
底数不变指数乘,
推广指数一次幂,
逆用性质巧计算.
知识点1 幂的乘方
新课讲解
(3) -[(a-b)3 ]4 = -(a-b)3×4= -(a-b)12 .
计算:(1) (an+1)2 ; (2) [(-x)7]4 ; (3) -[(a-b)3 ]4 .
解:(1) (an+1)2 = a(n+1)×2 = a2n+2 ;
(2) [(-x)7]4 = (-x)7×4 = (-x)28= x28 ;
新课讲解
已知 a2n=3,求 a4n-a6n 的值.
解:a4n-a6n = (a2n)2- (a2n)3
= 32-33
= -18 .
把指数是积的形式的幂写成幂的乘方,amn=(am)n
(m,n都是正整数),然后整体代入,求出式子的值.
课堂小结
幂的乘方
(am)n=amn (m,n为正整数)
性质:幂的乘方,底数不变,指数相乘.
当堂小练
3. (1)若2x+y=3,则4x·2y= .
(2)已知3m·9m·27m·81m=330,求m的值.
8
解:3m·32m·33m·34m=330
310m=330
m=3
(1)探究:根据乘方的意义填空,观察计算结果,你能发现什么规律?
①23×24=(2×2×2)×(2×2×2×2)=2( );
②a3·a4= =a( );
③5m×5n=×=5( ).
知识点 1
同底数幂的乘法法则
7
(a·a·a)·(a·a·a·a)
7
m+n
发现:同底数幂相乘,底数 ,指数 .
(2)am·an= (m,n都是正整数).
(3)am·an·ap= (m,n,p都是正整数).
不变
相加
am+n
am+n+p
(1)由am·an=am+n,反过来,可得
am+n= (m,n都是正整数).
(2)逆用法则时,要注意指数是加法运算,幂之间是乘法运算.
知识点 2
逆用同底数幂乘法法则解决问题
am·an
2.(1)已知2m=1,2n=3,则2m+n=( )
A.2 B.3
C.4 D.6
(2)已知am=3,an=2,则am+n= .
B
6
在具体做题时,要注意先运用同底数幂的乘法法则进行乘法运算,再进行加减运算.
知识点 3
同底数幂的乘法与加减法混合运算
3.(1)下列各式中计算结果为x5的是( )
A.x3+x2 B.x3·x2
C.x·x3 D.x7-x2
(2)计算:a2·a5+a·a3·a3.
解:原式=a2+5+a1+3+3=a7+a7=2a7.
B
4.【例1】(1)(2024苏州)x3·x2= ;
(2)a·a9·a2= .
x5
a12
9.(1)化简-a2·a4的结果是 ;
(2)若am·a2=a7,则m的值为 .
-a6
5
10.(1)(x-y)3(x-y)2= ;
(2)(x-y)(x-y)n-3= ;
(3)(2024河北模拟)若3a=2,3b=5,则3a+b= .
(x-y)5
(x-y)n-2
10
6.计算:103·10m-1·102m+2.
解:原式=103+m-1+2m+2=103m+4.
11.(2024宿迁二模)已知am+n=12,an=4,求am的值.
解:因为am+n=am·an=12,且an=4,
所以4am=12,所以am=3.
7.【例4】(跨学科融合)(核心教材母题:北师7下P1、人教8上P98)光在真空中的速度约为3×108 m/s,太阳光照射到地球上大约需要 5× 102 s.地球距离太阳大约有多远?
解:3×108×5×102=15×1010=1.5×1011(m).
答:地球距离太阳大约有1.5×1011 m.
核心教材母题:教材是新中考命题的依据,近年来中考数学卷中都有较多题的素材来源于北师大版和人教版教材.本书将两个版本重合的教材母题进行汇总,并作为课堂例习题呈现.
★13. (运算能力)已知 8×2a×=210,且 2a+b=
8,求 ab 的值.
解:因为8×2a×=22a+4=210,
所以2a+4=10.解得a=3.
因为2a+b=8,a=3,所以b=2.
所以ab=32=9.
0.50
备注:每课时带★的题目为提高题.难度系数越小,题目越难.
布置作业
请完成完成课后对应习题
THANKS
北师大版七年级数学下册课件
第一章 整式的乘除
1.1幂的乘除
课时1——同底数幂的乘法
1.了解幂的乘方的运算法则,熟练运用幂的乘方的运算法则进行实际计算.(重点)
2.掌握幂的乘方的运算法则的推导.(难点)
3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.
学习目标
新课导入
(1) (x2)2 = x2 2= x4 ;
(2) (x2)3 = x2 3= x6 .
观察计算结果,你能发现什么规律?
(1) (x2)2 = x2 x2 = x2+2= x4 ;
(2) (x2)3 = x2 x2 x2 = x2+2+2= x6 .
结 论
新课导入
观察计算结果,你能发现什么规律?(m,n为正整数)
(1) (32)3=32×32×32=36 ;
(2) (a2)3=a2×a2×a2=a6 ;
(3) (am)3=am×am×am=a3m (m是正整数);
(4) (am)n=am×am× am=amn (m,n为正整数).
n个am
新课导入
规 律
以上式子都是幂的乘方的形式,根据已经学过的乘方的意义和同底数幂的乘法性质可以得出幂的乘方的结果中底数不变,指数为两个指数的乘积(其中指数均为正整数).
思考:你能总结出幂的乘方的运算法则吗
新课讲解
知识点1 幂的乘方
性质:幂的乘方,底数不变,指数相乘.
n个m
n个am
符号表示:(am)n=amn(m,n都是正整数).
一般地,对于任意底数a与任意正整数m,n.
(am)n=am×am× am=amn
=a(m+m+m+ +m)
新课讲解
知识点1 幂的乘方
示例:
= = = =
底数a不变
指数相乘
底数x+y不变
指数相乘
新课讲解
(1) 幂的乘方的性质也可以推广为 [(am)n]p=amnp
(m,n,p都为正整数).
(2) 幂的乘方的性质可以逆用,即 amn=(am)n (m,n为正整数).
知识点1 幂的乘方
新课讲解
(1)在形式上,幂的乘方的底数本身就是一个幂,根据乘方的意义和同底数幂的乘法的性质可以推出幂的乘方的性质;
(2)在幂的乘方中,底数可以是单项式,也可以是多项式.
幂的乘方用性质,
底数不变指数乘,
推广指数一次幂,
逆用性质巧计算.
知识点1 幂的乘方
新课讲解
(3) -[(a-b)3 ]4 = -(a-b)3×4= -(a-b)12 .
计算:(1) (an+1)2 ; (2) [(-x)7]4 ; (3) -[(a-b)3 ]4 .
解:(1) (an+1)2 = a(n+1)×2 = a2n+2 ;
(2) [(-x)7]4 = (-x)7×4 = (-x)28= x28 ;
新课讲解
已知 a2n=3,求 a4n-a6n 的值.
解:a4n-a6n = (a2n)2- (a2n)3
= 32-33
= -18 .
把指数是积的形式的幂写成幂的乘方,amn=(am)n
(m,n都是正整数),然后整体代入,求出式子的值.
课堂小结
幂的乘方
(am)n=amn (m,n为正整数)
性质:幂的乘方,底数不变,指数相乘.
当堂小练
3. (1)若2x+y=3,则4x·2y= .
(2)已知3m·9m·27m·81m=330,求m的值.
8
解:3m·32m·33m·34m=330
310m=330
m=3
(1)探究:根据乘方的意义填空,观察计算结果,你能发现什么规律?
①23×24=(2×2×2)×(2×2×2×2)=2( );
②a3·a4= =a( );
③5m×5n=×=5( ).
知识点 1
同底数幂的乘法法则
7
(a·a·a)·(a·a·a·a)
7
m+n
发现:同底数幂相乘,底数 ,指数 .
(2)am·an= (m,n都是正整数).
(3)am·an·ap= (m,n,p都是正整数).
不变
相加
am+n
am+n+p
(1)由am·an=am+n,反过来,可得
am+n= (m,n都是正整数).
(2)逆用法则时,要注意指数是加法运算,幂之间是乘法运算.
知识点 2
逆用同底数幂乘法法则解决问题
am·an
2.(1)已知2m=1,2n=3,则2m+n=( )
A.2 B.3
C.4 D.6
(2)已知am=3,an=2,则am+n= .
B
6
在具体做题时,要注意先运用同底数幂的乘法法则进行乘法运算,再进行加减运算.
知识点 3
同底数幂的乘法与加减法混合运算
3.(1)下列各式中计算结果为x5的是( )
A.x3+x2 B.x3·x2
C.x·x3 D.x7-x2
(2)计算:a2·a5+a·a3·a3.
解:原式=a2+5+a1+3+3=a7+a7=2a7.
B
4.【例1】(1)(2024苏州)x3·x2= ;
(2)a·a9·a2= .
x5
a12
9.(1)化简-a2·a4的结果是 ;
(2)若am·a2=a7,则m的值为 .
-a6
5
10.(1)(x-y)3(x-y)2= ;
(2)(x-y)(x-y)n-3= ;
(3)(2024河北模拟)若3a=2,3b=5,则3a+b= .
(x-y)5
(x-y)n-2
10
6.计算:103·10m-1·102m+2.
解:原式=103+m-1+2m+2=103m+4.
11.(2024宿迁二模)已知am+n=12,an=4,求am的值.
解:因为am+n=am·an=12,且an=4,
所以4am=12,所以am=3.
7.【例4】(跨学科融合)(核心教材母题:北师7下P1、人教8上P98)光在真空中的速度约为3×108 m/s,太阳光照射到地球上大约需要 5× 102 s.地球距离太阳大约有多远?
解:3×108×5×102=15×1010=1.5×1011(m).
答:地球距离太阳大约有1.5×1011 m.
核心教材母题:教材是新中考命题的依据,近年来中考数学卷中都有较多题的素材来源于北师大版和人教版教材.本书将两个版本重合的教材母题进行汇总,并作为课堂例习题呈现.
★13. (运算能力)已知 8×2a×=210,且 2a+b=
8,求 ab 的值.
解:因为8×2a×=22a+4=210,
所以2a+4=10.解得a=3.
因为2a+b=8,a=3,所以b=2.
所以ab=32=9.
0.50
备注:每课时带★的题目为提高题.难度系数越小,题目越难.
布置作业
请完成完成课后对应习题
THANKS
同课章节目录
