南京市鼓楼区2015-2016学年高二下期中考试文科数学试题含答案
文档属性
| 名称 | 南京市鼓楼区2015-2016学年高二下期中考试文科数学试题含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 43.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-03 00:00:00 | ||
图片预览


文档简介
高二数学(文科)
参考公式:
样本数据x1,x2,…,xn的方差:eq s\s(2)= \f(1,n)\I\su(i=1,n,(x\s\do2(i)-)\s(2)) ,其中=.
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答卷纸相应位置上.
1.已知复数z=1+2i,则复数 在复平面内对应的点位于第 ▲ 象限.
2.某班有52人,现用系统抽样的方法,抽 ( http: / / www.21cnjy.com )取一个容量为4的样本,已知编号分别为6,32,45的同学都在样本中,那么样本中另一位同学的编号是 ▲ .
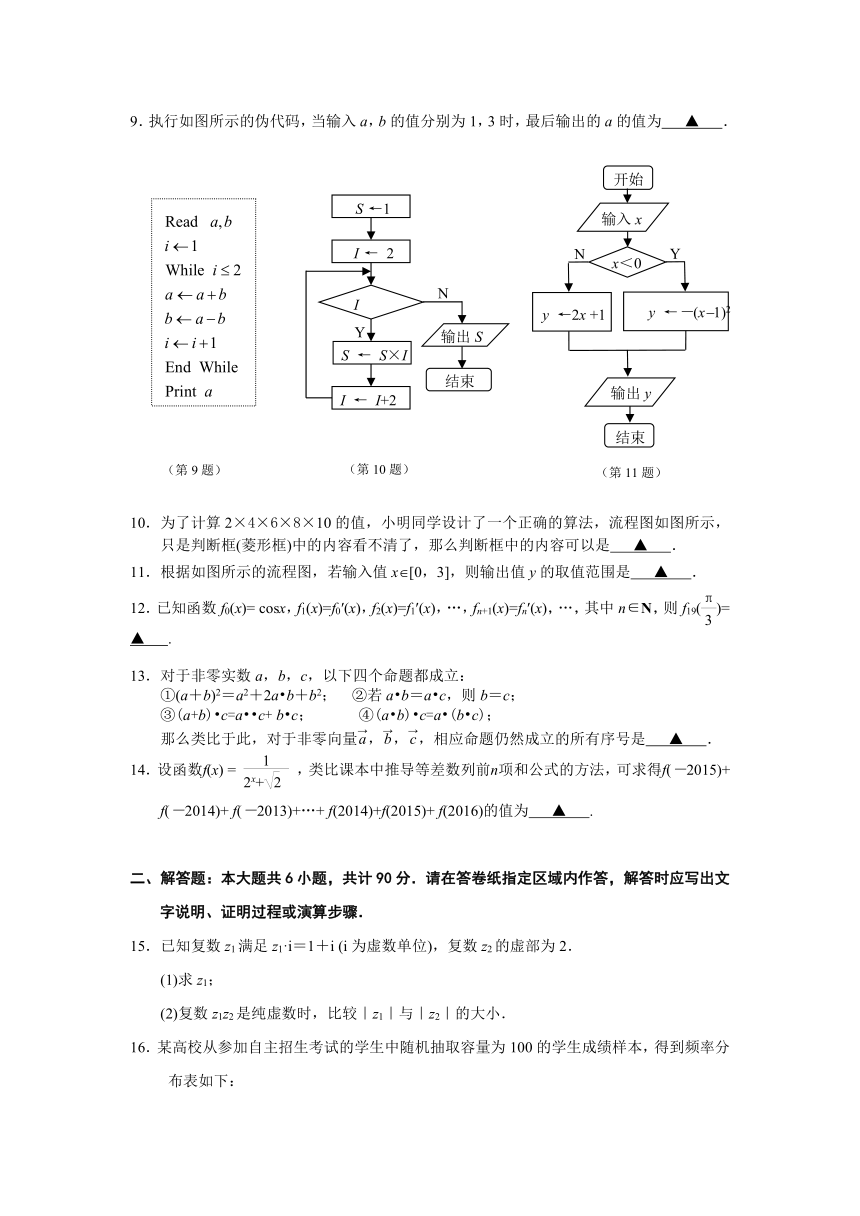
3.交通部门对某段公路上汽车的速度实施监控 ( http: / / www.21cnjy.com ),并从速度在50~90 km/h的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在70 km/h以下的汽车有 ▲ 辆.
4.已知如图是一位篮球运动员在6场比赛中得分的茎叶图,那么该组数据的方差为 ▲ .
5.根据如图所示的伪代码,可知输出的结果S为 ▲ .
6.某教师出了一份三道题的测试卷,每道题1 ( http: / / www.21cnjy.com )分,全班得3分、2分、1分和0分的学生所占比例分别为30%、50%、10%和10%,则全班学生的平均分为 ▲ 分.
7.某人射击1次,命中8~10环的概率如下表所示:
命中环数 10环 9环 8环
概 率 0.12 0.18 0.28
则他射击1次,至少命中9环的概率为 ▲ .
8.在区间[-1,2]上随机取一个实数x,则x∈[0,1]的概率为 ▲ .
9.执行如图所示的伪代码,当输入a,b的值分别为1,3时,最后输出的a的值为 ▲ .
10.为了计算2×4×6× ( http: / / www.21cnjy.com )8×10的值,小明同学设计了一个正确的算法,流程图如图所示,只是判断框(菱形框)中的内容看不清了,那么判断框中的内容可以是 ▲ .
11.根据如图所示的流程图,若输入值x[0,3],则输出值y的取值范围是 ▲ .
12.已知函数f0(x)= cosx, ( http: / / www.21cnjy.com )f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),…,其中n∈N,则f19()= ▲ .
13.对于非零实数a,b,c,以下四个命题都成立:
①(a+b)2=a2+2a b+b2; ②若a b=a c,则b=c;
③(a+b) c=a c+ b c; ④(a b) c=a (b c);
那么类比于此,对于非零向量,,,相应命题仍然成立的所有序号是 ▲ .
14.设函数f(x) = eq \f(1,2x+) ,类比课本中推导等差数列前n项和公式的方法,可求得f(-2015)+ f(-2014)+ f(-2013)+…+ f(2014)+f(2015)+ f(2016)的值为 ▲ .
二、解答题:本大题共6小题,共计90分.请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.已知复数z1满足z1·i=1+i (i为虚数单位),复数z2的虚部为2.
(1)求z1;
(2)复数z1z2是纯虚数时,比较|z1|与|z2|的大小.
16.某高校从参加自主招生考试的学生中随机抽取容量为100的学生成绩样本,得到频率分布表如下:
组号 分组 频数 频率
第一组 24 0.24
第二组 16 ②
第三组 ① 0.3
第四组 20 0.20
第五组 10 0.10
合 计 100 1.00
(1)上表中①②位置的数据分别是多少?
(2)为了更多了解第三组、第四组、第五组的学生情况,该高校决定在这三个组中用分
层抽样法抽取6名学生进行考察,这三个组参加考核的人数分别是多少?
17. (本题满分14分)
(1)不透明的袋子中装有除颜色外其它都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,求这2只球颜色不同的概率;
(2)已知关于x的一元二次方程x2 ( http: / / www.21cnjy.com )-2bx+c2=0,其中b是从0、1、2、3四个数中随机取出的一个数,c是从0、1、2三个数中随机取出的一个数,求这个方程没有实根的概率.
18.已知数列{an}满足a1=3,an+1·an-2·an+1=0 (n∈N*).
(1)求,,的值;
(2)求{an}的通项公式.
19.已知椭圆+=1(a>b>0)的离心率为 EQ \F(,3),且过点A(0,1),
(1)求椭圆的方程;
(2)过点A作两条相互垂直的直线,分别交椭圆 ( http: / / www.21cnjy.com )于点M,N(M,N不与点A重合) .直线MN是否过定点?若过定点,则求出定点坐标;若不过定点,则请说明理由.
20.已知函数f(x)= .
(1)当e≤x≤e2时,求函数f(x)的最小值;
(2)已知函数g(x)=2x-,且f(x)g(x)≤0恒成立,求实数a的值;
(3)某同学发现:存在正实数m、n(m<n) ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ),使mn=nm ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ),试问:他的发现是否正确 若不正确,则请说明理由;若正确,则请直接写出m ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )的取值范围,而不需要解答过程.
高二数学(文科)参考答案和评分标准
一、填空题:本大题共14小题,每小题5分,共计70分.
1.四 2.19 3.75 4. 5.16 6.2 7.0.3 8. 9.5
10.I≤10或I<11或I≤11或I<12或I<10.5,等 11.[1,7] 12. EQ \F(,2) 13.①③
14.1008
二、解答题:本大题共6小题,共计90分.
15.(1)1-i;……………………………………………………………………………………6分
(2) z2=-2+i,…………………………………………………………………………10分
|z1|=,
|z2|=2,……………………………………………………………………………12分
|z1|<|z2|.…………………………………………………………………………14分
16.(1)100-(16+24+20+10)=30或100×0.3=30,………………………………………3分
1-(0.24+0.3+0.20+0.10)=0.16或16÷100=0.16;…………………………………6分
(没有任何过程,最多得4分)
(2) =0.1,………………………………………………………………………………8分
30×0.1=3,所以第三组参加考核的人数是3;………………………………………10分
类似地,第四组,第五组参加考核的人数分别是2,1.……………………………14分
17.(1)设事件A为“这2只球颜色不同”; -----……………………-----------------1分
基本事件共6个:(白,红),(白,黄1),(白,黄2),(红,黄1),(红,黄2),(黄1, 黄2),
事件A包含5个基本事件(白,红),(白,黄1),(白,黄2),(红,黄1),(红,黄2),----4分
因为每个基本事件发生的可能性都相同, ----------------------5分
所以,事件A发生的概率P(A)=. ----------------------7分
(2)设事件B为“方程x2-2bx+c2=0无实根”; ------------------……………---8分
当Δ=4b2-4c2=4(b2-c2)<0,即b<c时,方程x2-2bx+c2=0无实根.
基本事件共12个:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).其中第一个数表示b的取值,第二个数表示c的取值.--…………--4分
事件B包含3个基本事件(0,1),(0,2),(1,2),--…………………………………---11分
因为每个基本事件发生的可能性都相同, ----------------------12分
所以事件B发生的概率P(A)==. ----------------------14分
(第(1)小题,有一点过程且结果正确,得7分;第(2)小题,至少交待清楚三个数据12,3和的由来才能得7分)
18.(1)由an+1an=2·an-1得an+1=2-,…………………………………………………2分
代入a1=3,n依次取值2,3,4,得
=,=,=,………………………………………………………6分
(2)猜想:{}是等差数列.
证明:由an+1·an=2·an-1变形,得
(an+1-1)·(an-1)=-(an+1-1)+(an-1),
即-=1在n∈N*时恒成立,
所以{}是等差数列.………………………………………………………………12分
由=,所以=+n-1,
变形得an-1=,…………………………………………………………………14分
所以an=为数列{an}的一个通项公式.…………………………………………16分
19.(1) +y =1;……………………………………………………………………………4分
(2)解法一
因为M,N不与点B重合,所以直线AM的斜率存在,且不为零.………………5分
设AM的斜率为k,则AN的斜率为-.
直线AM方程:y=kx+1,
直线AN方程:y=-x+1.
将AM方程代入椭圆,整理:(3k +1)x +6kx=0.………………………………………7分
则点M横坐标xM=-,纵坐标yM=.……………………………………9分
用-替换k可得点N横坐标xN=,纵坐标yN=.…………………………12分
直线MN方程: y= x-.……………………………………………………15分
由此,可知,过定点(0,-).………………………………………………………16分
解法二
设直线MN方程为y=kx+ m,
设M(x1,y1),N(x2,y2),
可得m=-.
20.(1) f(x)定义域为(0,+∞),f ′ (x)=.
令f ' (x)==0,则x=e.
列表如下:
x (0,e) e (e,+∞)
f ' (x) + 0 -
f(x) ↗ ↘
所以f(x)在区间(e,+∞)上单调减.
当e≤x≤e2时,函数f(x)单调减,所以,函数f(x)的最小值为f(e2) =2e-2.…4分
(2)f(x) g(x)≤0恒成立,即2ln x-ax+a≤0在x>0时恒成立.
令h(x) = f(x) g(x),则h′(x)=,x>0.
若a≤0,f′(x)>0,f(x)在(0,+∞)上单调递增;
若a>0,当x∈(0,)时,f′(x)>0,f(x)单调递增;
当x∈(,+∞)时,f′(x)<0,f(x)单调递减. ………………………………………6分
所以,若a≤0,则f(x)在(0,+∞)上单调递增,又f(1)=0,故f(x)≤0不恒成立.
……………………………………………………………………………………………8分
若a>2,则当x∈(,1)时,f(x)单调递减,f(x)>f(1)=0,不合题意,………………10分
若0f(1)=0,不合题意,……………12分
若a=2,f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,f(x)≤f(1)=0符合题意.
故a=2.…………………………………………………………………………………14分
(3)正确,m的取值范围是1<m<e.…………………………………………16分
理由如下,研究函数图像,f(x)在(0,e)上单调递增,在(e,+∞)上单调递减.
又∵当x→+∞时,f(x)→0.∴总存在正实数m,n且1<m<e<n,使得f(m)=f(n),即 = ,即mn=nm ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ).
S←0
For I From 1 To 7 step 2
S←S + I
End For
Print S
(第5题)
(第3题)
(第4题)
结束
x<0
输出y
(第11题)
输入x
y ←2x +1
Y
N
开始
S ←1
I ← 2
N
I
y ←-(x1)2
Y
输出S
结束
S ← S×I
I ← I+2
(第9题)
(第10题)
参考公式:
样本数据x1,x2,…,xn的方差:eq s\s(2)= \f(1,n)\I\su(i=1,n,(x\s\do2(i)-)\s(2)) ,其中=.
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答卷纸相应位置上.
1.已知复数z=1+2i,则复数 在复平面内对应的点位于第 ▲ 象限.
2.某班有52人,现用系统抽样的方法,抽 ( http: / / www.21cnjy.com )取一个容量为4的样本,已知编号分别为6,32,45的同学都在样本中,那么样本中另一位同学的编号是 ▲ .
3.交通部门对某段公路上汽车的速度实施监控 ( http: / / www.21cnjy.com ),并从速度在50~90 km/h的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在70 km/h以下的汽车有 ▲ 辆.
4.已知如图是一位篮球运动员在6场比赛中得分的茎叶图,那么该组数据的方差为 ▲ .
5.根据如图所示的伪代码,可知输出的结果S为 ▲ .
6.某教师出了一份三道题的测试卷,每道题1 ( http: / / www.21cnjy.com )分,全班得3分、2分、1分和0分的学生所占比例分别为30%、50%、10%和10%,则全班学生的平均分为 ▲ 分.
7.某人射击1次,命中8~10环的概率如下表所示:
命中环数 10环 9环 8环
概 率 0.12 0.18 0.28
则他射击1次,至少命中9环的概率为 ▲ .
8.在区间[-1,2]上随机取一个实数x,则x∈[0,1]的概率为 ▲ .
9.执行如图所示的伪代码,当输入a,b的值分别为1,3时,最后输出的a的值为 ▲ .
10.为了计算2×4×6× ( http: / / www.21cnjy.com )8×10的值,小明同学设计了一个正确的算法,流程图如图所示,只是判断框(菱形框)中的内容看不清了,那么判断框中的内容可以是 ▲ .
11.根据如图所示的流程图,若输入值x[0,3],则输出值y的取值范围是 ▲ .
12.已知函数f0(x)= cosx, ( http: / / www.21cnjy.com )f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),…,其中n∈N,则f19()= ▲ .
13.对于非零实数a,b,c,以下四个命题都成立:
①(a+b)2=a2+2a b+b2; ②若a b=a c,则b=c;
③(a+b) c=a c+ b c; ④(a b) c=a (b c);
那么类比于此,对于非零向量,,,相应命题仍然成立的所有序号是 ▲ .
14.设函数f(x) = eq \f(1,2x+) ,类比课本中推导等差数列前n项和公式的方法,可求得f(-2015)+ f(-2014)+ f(-2013)+…+ f(2014)+f(2015)+ f(2016)的值为 ▲ .
二、解答题:本大题共6小题,共计90分.请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.已知复数z1满足z1·i=1+i (i为虚数单位),复数z2的虚部为2.
(1)求z1;
(2)复数z1z2是纯虚数时,比较|z1|与|z2|的大小.
16.某高校从参加自主招生考试的学生中随机抽取容量为100的学生成绩样本,得到频率分布表如下:
组号 分组 频数 频率
第一组 24 0.24
第二组 16 ②
第三组 ① 0.3
第四组 20 0.20
第五组 10 0.10
合 计 100 1.00
(1)上表中①②位置的数据分别是多少?
(2)为了更多了解第三组、第四组、第五组的学生情况,该高校决定在这三个组中用分
层抽样法抽取6名学生进行考察,这三个组参加考核的人数分别是多少?
17. (本题满分14分)
(1)不透明的袋子中装有除颜色外其它都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,求这2只球颜色不同的概率;
(2)已知关于x的一元二次方程x2 ( http: / / www.21cnjy.com )-2bx+c2=0,其中b是从0、1、2、3四个数中随机取出的一个数,c是从0、1、2三个数中随机取出的一个数,求这个方程没有实根的概率.
18.已知数列{an}满足a1=3,an+1·an-2·an+1=0 (n∈N*).
(1)求,,的值;
(2)求{an}的通项公式.
19.已知椭圆+=1(a>b>0)的离心率为 EQ \F(,3),且过点A(0,1),
(1)求椭圆的方程;
(2)过点A作两条相互垂直的直线,分别交椭圆 ( http: / / www.21cnjy.com )于点M,N(M,N不与点A重合) .直线MN是否过定点?若过定点,则求出定点坐标;若不过定点,则请说明理由.
20.已知函数f(x)= .
(1)当e≤x≤e2时,求函数f(x)的最小值;
(2)已知函数g(x)=2x-,且f(x)g(x)≤0恒成立,求实数a的值;
(3)某同学发现:存在正实数m、n(m<n) ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ),使mn=nm ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ),试问:他的发现是否正确 若不正确,则请说明理由;若正确,则请直接写出m ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )的取值范围,而不需要解答过程.
高二数学(文科)参考答案和评分标准
一、填空题:本大题共14小题,每小题5分,共计70分.
1.四 2.19 3.75 4. 5.16 6.2 7.0.3 8. 9.5
10.I≤10或I<11或I≤11或I<12或I<10.5,等 11.[1,7] 12. EQ \F(,2) 13.①③
14.1008
二、解答题:本大题共6小题,共计90分.
15.(1)1-i;……………………………………………………………………………………6分
(2) z2=-2+i,…………………………………………………………………………10分
|z1|=,
|z2|=2,……………………………………………………………………………12分
|z1|<|z2|.…………………………………………………………………………14分
16.(1)100-(16+24+20+10)=30或100×0.3=30,………………………………………3分
1-(0.24+0.3+0.20+0.10)=0.16或16÷100=0.16;…………………………………6分
(没有任何过程,最多得4分)
(2) =0.1,………………………………………………………………………………8分
30×0.1=3,所以第三组参加考核的人数是3;………………………………………10分
类似地,第四组,第五组参加考核的人数分别是2,1.……………………………14分
17.(1)设事件A为“这2只球颜色不同”; -----……………………-----------------1分
基本事件共6个:(白,红),(白,黄1),(白,黄2),(红,黄1),(红,黄2),(黄1, 黄2),
事件A包含5个基本事件(白,红),(白,黄1),(白,黄2),(红,黄1),(红,黄2),----4分
因为每个基本事件发生的可能性都相同, ----------------------5分
所以,事件A发生的概率P(A)=. ----------------------7分
(2)设事件B为“方程x2-2bx+c2=0无实根”; ------------------……………---8分
当Δ=4b2-4c2=4(b2-c2)<0,即b<c时,方程x2-2bx+c2=0无实根.
基本事件共12个:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).其中第一个数表示b的取值,第二个数表示c的取值.--…………--4分
事件B包含3个基本事件(0,1),(0,2),(1,2),--…………………………………---11分
因为每个基本事件发生的可能性都相同, ----------------------12分
所以事件B发生的概率P(A)==. ----------------------14分
(第(1)小题,有一点过程且结果正确,得7分;第(2)小题,至少交待清楚三个数据12,3和的由来才能得7分)
18.(1)由an+1an=2·an-1得an+1=2-,…………………………………………………2分
代入a1=3,n依次取值2,3,4,得
=,=,=,………………………………………………………6分
(2)猜想:{}是等差数列.
证明:由an+1·an=2·an-1变形,得
(an+1-1)·(an-1)=-(an+1-1)+(an-1),
即-=1在n∈N*时恒成立,
所以{}是等差数列.………………………………………………………………12分
由=,所以=+n-1,
变形得an-1=,…………………………………………………………………14分
所以an=为数列{an}的一个通项公式.…………………………………………16分
19.(1) +y =1;……………………………………………………………………………4分
(2)解法一
因为M,N不与点B重合,所以直线AM的斜率存在,且不为零.………………5分
设AM的斜率为k,则AN的斜率为-.
直线AM方程:y=kx+1,
直线AN方程:y=-x+1.
将AM方程代入椭圆,整理:(3k +1)x +6kx=0.………………………………………7分
则点M横坐标xM=-,纵坐标yM=.……………………………………9分
用-替换k可得点N横坐标xN=,纵坐标yN=.…………………………12分
直线MN方程: y= x-.……………………………………………………15分
由此,可知,过定点(0,-).………………………………………………………16分
解法二
设直线MN方程为y=kx+ m,
设M(x1,y1),N(x2,y2),
可得m=-.
20.(1) f(x)定义域为(0,+∞),f ′ (x)=.
令f ' (x)==0,则x=e.
列表如下:
x (0,e) e (e,+∞)
f ' (x) + 0 -
f(x) ↗ ↘
所以f(x)在区间(e,+∞)上单调减.
当e≤x≤e2时,函数f(x)单调减,所以,函数f(x)的最小值为f(e2) =2e-2.…4分
(2)f(x) g(x)≤0恒成立,即2ln x-ax+a≤0在x>0时恒成立.
令h(x) = f(x) g(x),则h′(x)=,x>0.
若a≤0,f′(x)>0,f(x)在(0,+∞)上单调递增;
若a>0,当x∈(0,)时,f′(x)>0,f(x)单调递增;
当x∈(,+∞)时,f′(x)<0,f(x)单调递减. ………………………………………6分
所以,若a≤0,则f(x)在(0,+∞)上单调递增,又f(1)=0,故f(x)≤0不恒成立.
……………………………………………………………………………………………8分
若a>2,则当x∈(,1)时,f(x)单调递减,f(x)>f(1)=0,不合题意,………………10分
若0
若a=2,f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,f(x)≤f(1)=0符合题意.
故a=2.…………………………………………………………………………………14分
(3)正确,m的取值范围是1<m<e.…………………………………………16分
理由如下,研究函数图像,f(x)在(0,e)上单调递增,在(e,+∞)上单调递减.
又∵当x→+∞时,f(x)→0.∴总存在正实数m,n且1<m<e<n,使得f(m)=f(n),即 = ,即mn=nm ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ).
S←0
For I From 1 To 7 step 2
S←S + I
End For
Print S
(第5题)
(第3题)
(第4题)
结束
x<0
输出y
(第11题)
输入x
y ←2x +1
Y
N
开始
S ←1
I ← 2
N
I
y ←-(x1)2
Y
输出S
结束
S ← S×I
I ← I+2
(第9题)
(第10题)
同课章节目录
