整式的乘法二

课件17张PPT。整式的乘法 15.1例如； (-3x3y)(-5x4y2z4)=_______;
例如： -3ab2(-4a+3ab-2)
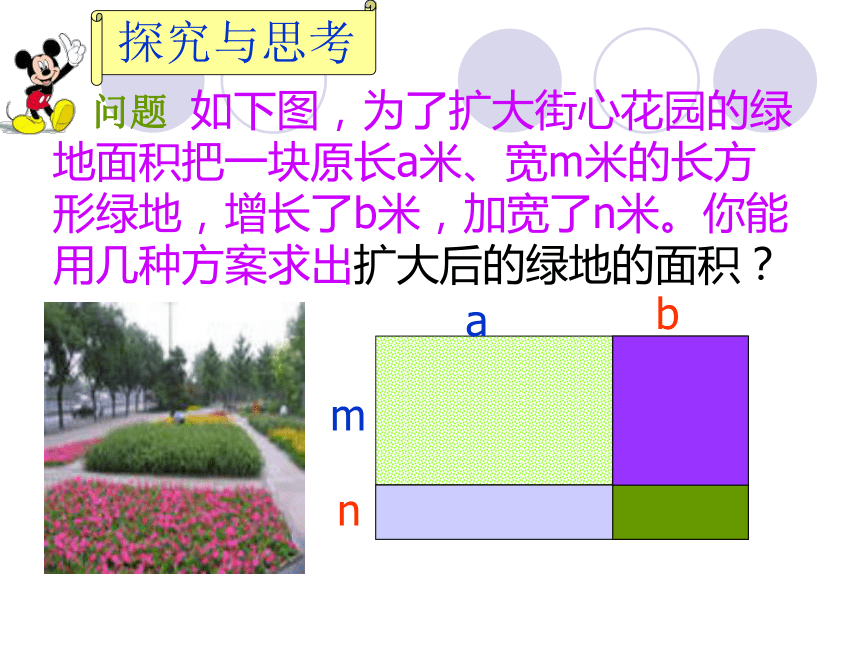
=________________15x7y3z412a2b2-9a2b3+6ab2你还记得吗？1 .单项式与单项式相乘的方法？2. 单项式与多项式相乘的方法？　问题 如下图，为了扩大街心花园的绿地面积把一块原长a米、宽m米的长方形绿地，增长了b米，加宽了n米。你能用几种方案求出扩大后的绿地的面积？
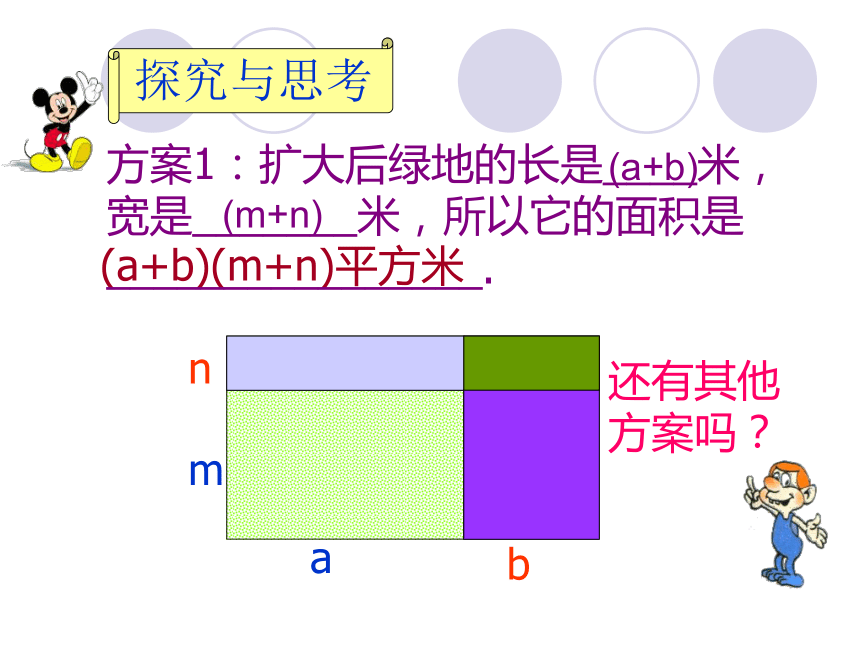
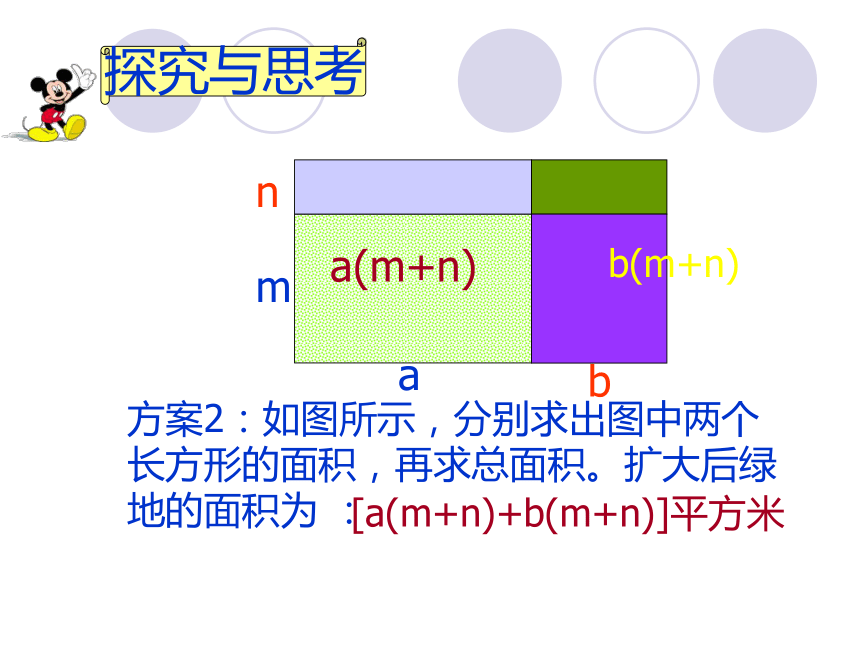
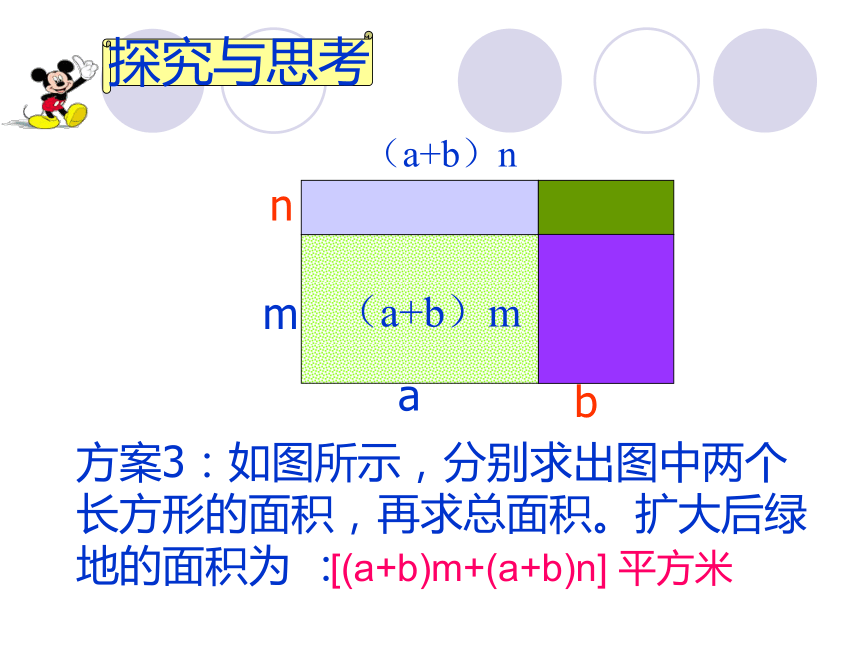
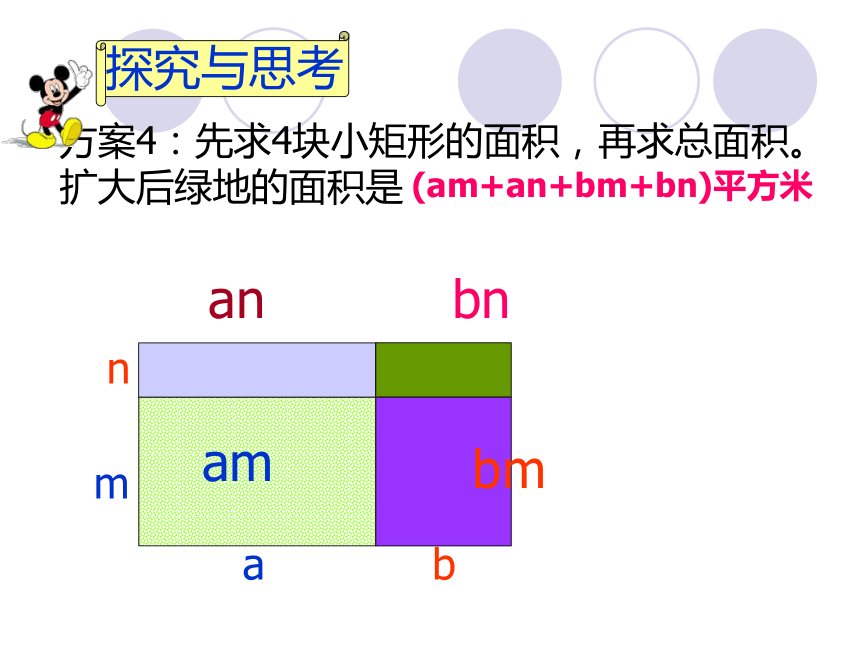
nbma探究与思考　方案1 s=nbma(a+b)(m+n)平方米方案1：扩大后绿地的长是____米，宽是_______米，所以它的面积是________________. 探究与思考还有其他方案吗？还有其他方案吗？(a+b)(m+n)nma方案2：如图所示，分别求出图中两个长方形的面积，再求总面积。扩大后绿地的面积为 ： a(m+n)b(m+n)[a(m+n)+b(m+n)]平方米b(m+n)+探究与思考。bma方案3：如图所示，分别求出图中两个长方形的面积，再求总面积。扩大后绿地的面积为 ： （a+b）m（a+b）n探究与思考[(a+b)m+(a+b)n] 平方米maamanbmbn(am+an+bm+bn)平方米anbmbn+++方案4：先求4块小矩形的面积，再求总面积。扩大后绿地的面积是探究与思考观察这几个式子： (a+b)(m+n) am+an+bm+bn （a+b）m+（a+b）n a（m+n）+b（m+n）你能说出它们有何关系吗？分析与比较===(a+b)(m+n)=am1234+an+bm+bn 你会说吗？由此你能得到什么启发？多项式与多项式相乘的方法：多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.也就是: (a+b)(m+n) = am+an+bm+bn用上面的方法试一试(a-b)(m-n)=am-an-bm+bn例 计算：
(1) ( 3x + 1 )( x + 2 ) ;
(2) ( x – 8 y )( x – y ) .
解 (1)原式 = 3x · x + 3x ·2 + 1·x + 1×2 (2 )原式 = x · x – x · y – 8y · x + 8y ·y= 3 x2 +6 x + x +2=3x2 + 7x + 2 = x 2 - x y – 8xy + 8y2 = x 2 - 9xy + 8y2 提示：
1.做到不重不漏
2.注意符号
3.结果化为最简形式学以致用
(1) (2x+1)(x+3); (2) (a+3b)(a –3b ).
(3) (x-2)(x +4) (4) (x-y)(x +xy+y )
答案: (1) 2x2+7x+3;


学以至用大显身手比一比 看谁做的快22232332（2）a -9b(4) x -y(3) x +2x-8
(x+2)(x+3) =
(x-4)(x+1) =
(a+4)(a-2) =
(y-5)(y -3) =
根据上面计算的结果，你有什么发现？ (x+p)(x+q）=( ) +( )x+( )再上新台阶做做看x + 5x+6x – 3x-4a + 2a-8y - 8y+1522222xp+qpqxpxqx2pxqx观察右图，填空xxpqpqpxqxx2试一试：
确定下列各式中m的值:（口答）
(1) (x+4)(x+9) = x2 + m x + 36
(2) (x-2)(x-18) = x + m x +36
(3) (x+3)(x+12) = x + m x +36
(4) (x-6) (x-p) = x + m x + 36

(1) m =13 (2) m = - 20 (3) m= 15(4) p= 6, m= -12(5) p= 4,q= 9, m=13 p=2,q = 18, m=20 p = 3, q =12, m=15 p=6, q= 6, m=122222 提个醒：
（1）利用下式
(x+p)(x+q）
= x +(p+q)x+pq
（2）注意符号
xp+q2pqP=1, q=36, m=37快速说出结果 (1)（x-5) (x- 6)=
(2) (x+4) (x+3)=
(3) (x+2) (x- 6)=
(4) (x-6) (x+6)=我的收获：本节课我学会了……单项式乘以多项式的依据是什么？如何进行单项式与多项式乘法运算？ 多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)( m+n)=am+an+bm+bn。(x+p)(x+q) = x + (p+q) x + p q2乘,先用一个多项式的每一项乘另一个多项乘,先用一个多项式的每一项乘另一个多项（1）多项式与多项式相乘，仍得多项式(2) 注意确定积中的每一项的符号，多项 式中每一项都包括它前面的符号. （3）最后结果要化为最简形式我还知道了(2)课外作业:
必做题： 课本P.149 第5题，

选做题： 解方程与不等式:
(1) (x-3)(x-2)+18 = (x+9)(x+1);
(2) (3x+4)(3x-4) ＜9(x-2)(x+3).
第10题谢谢各位领导老师莅临指导！Bye！谢谢合作