18.1.2平行四边形的判定
文档属性
| 名称 | 18.1.2平行四边形的判定 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-02 00:00:00 | ||
图片预览



文档简介
课件16张PPT。18.2.1平行四边形的判定(1)海南华侨中学平行四边
形的性质:对角相等邻角互补对角线
互相平分BACO∵四边形ABCD
是平行边形 ∴OA=OC,OB=OD中心对称图形D对边平行对边相等∵四边形ABCD
是平行四边形 定义:两组对边分别平行的四边形是平行四边形。∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= 180°,∠A+∠D=180°∵四边形ABCD
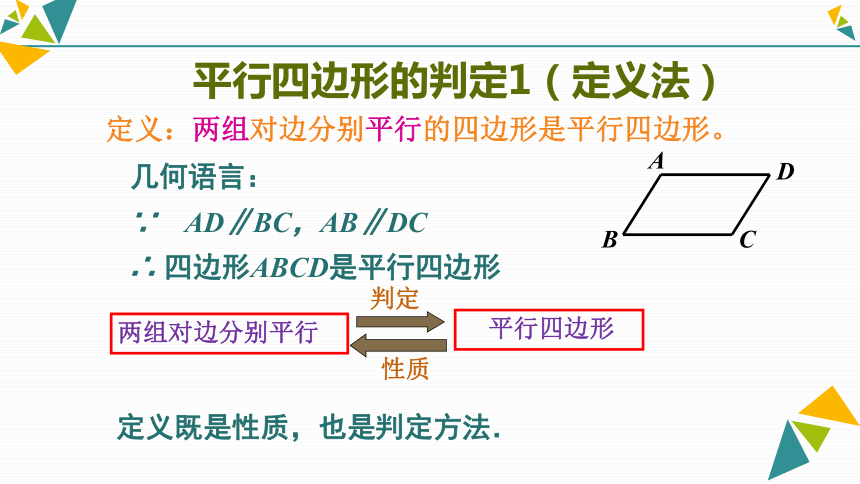
是平行边形 1.复习回顾两组对边分别平行 平行四边形性质判定定义既是性质,也是判定方法.几何语言:平行四边形的判定1(定义法)定义:两组对边分别平行的四边形是平行四边形。∵ AD∥BC,AB∥DC
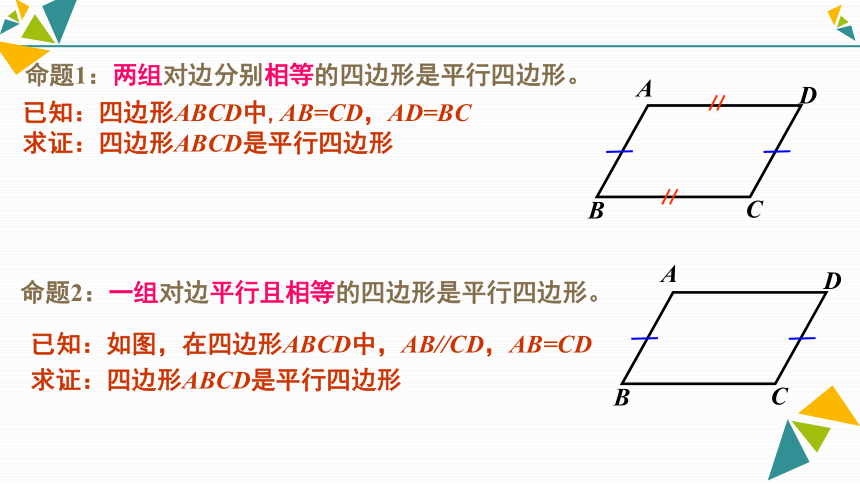
∴ 四边形ABCD是平行四边形 如图所示,某小区内修了两条相交公路,记为线段AB和线段BC.小区物业要以两条路为邻边修建一个平行四边形绿化带,请你帮物业想一想,如何确定平行四边形另外两边?2.情景引入命题1:两组对边分别相等的四边形是平行四边形。已知:四边形ABCD中,AB=CD,AD=BC
求证:四边形ABCD是平行四边形BDAC命题2:一组对边平行且相等的四边形是平行四边形。已知:如图,在四边形ABCD中,AB//CD,AB=CD
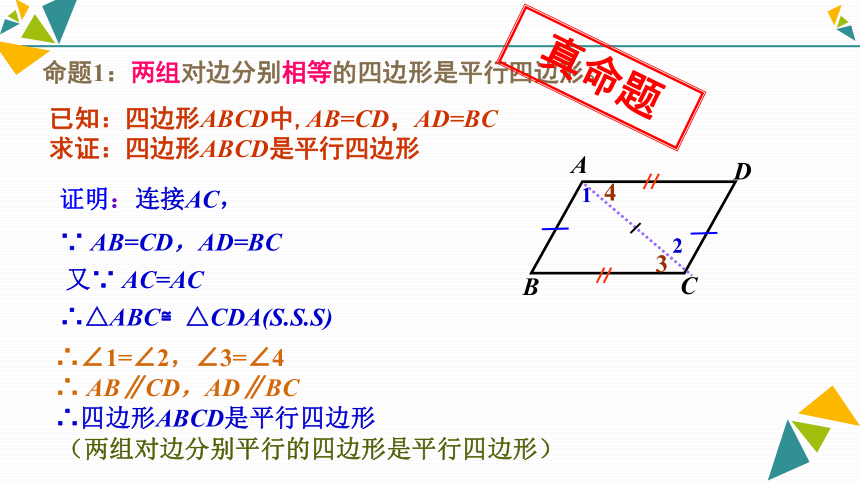
求证:四边形ABCD是平行四边形 BCDA已知:四边形ABCD中,AB=CD,AD=BC
求证:四边形ABCD是平行四边形∵ AB=CD,AD=BC
又∵ AC=AC
∴△ABC≌△CDA(S.S.S)
证明:连接AC,命题1:两组对边分别相等的四边形是平行四边形。∴∠1=∠2,∠3=∠4
∴ AB∥CD,AD∥BC
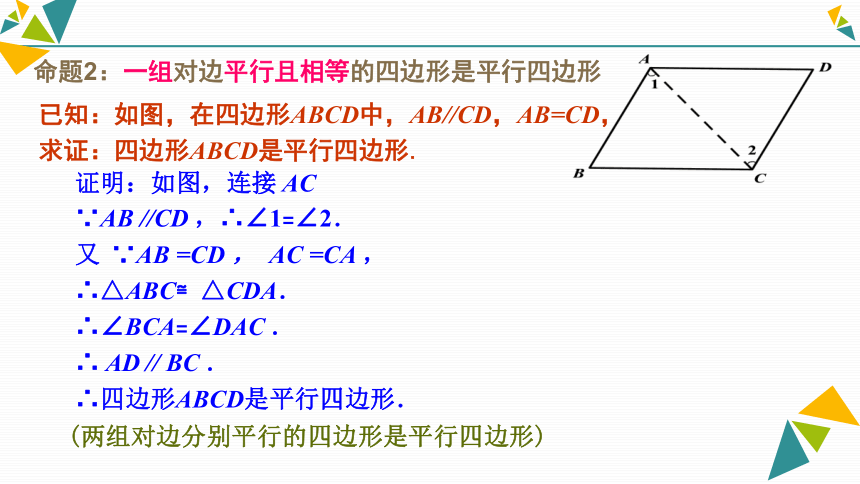
∴四边形ABCD是平行四边形真命题(两组对边分别平行的四边形是平行四边形)已知:如图,在四边形ABCD中,AB//CD,AB=CD,
求证:四边形ABCD是平行四边形. 证明:如图,连接 AC
∵AB //CD ,∴∠1=∠2.
又 ∵AB =CD , AC =CA ,
∴△ABC≌△CDA.
∴∠BCA=∠DAC .
∴ AD // BC .
∴四边形ABCD是平行四边形.命题2:一组对边平行且相等的四边形是平行四边形(两组对边分别平行的四边形是平行四边形)已知:四边形ABCD中,AB=CD,AD=BC
求证:四边形ABCD是平行四边形BDAC命题1:两组对边分别相等的四边形是平行四边形。 四边形ABCD是平行四边形AB∥ CD,AD ∥ BC△ABC≌△CDA∠1=∠2, ∠3=∠4(S.S.S)平行四边形三角形(证明角相等)思路:定义法转
化连
接
对
角
线 两组对边分别相等的四边形是平行四边形。判定定理1∵ AD=CB,AB=DC,
∴ 四边形ABCD是平行四边形 几何语言:3.归纳定理一组对边平行且相等的四边形是平行四边形判定定理2∴四边形ABCD是平行四边形.几何语言:强调:同一组对边平行且相等.AB∥CD且AB=CD,记作“AB CD”读作:“AB平行且等于CD”在四边形ABCD中,
∵AB//CD,AB =CD, 一组对边平行,另一组对边相等的四边形是平行四边形吗?假命题3.归纳定理4.知识梳理1.如图,在四边形ABCD中,AD=BC,要使四边形ABCD为平行四边形,可以添加的条件是 _______.(添加一个即可)
2.在四边形ABCD中,BD是对角线,下列条件中,不能判断四边形ABCD是平行四边形的是( )A.AB=CD, AD=BC
B.AB∥CD,∠1=∠2
C.AD=BC, ∠1=∠2
D.AB=CD, ∠1=∠2AD∥BC(或AB=CD)5.小试牛刀D试试看,哪位同学答得又快又准!例.如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AF=CE.
求证:四边形AECF是平行四边形. 证明:∵四边形ABCD是平行四边形
∴AD∥ CB(平行四边形的对边平行)
即:AF∥ CE
又∵ AF=CE
∴ AECF是平行四边形(一组对边平行且相等的四边形是平行四边形)思考:你还有别的方法吗?6.例题精析(1)本节课学习了哪几种判定平行四边形的方法?
(2)这些方法是从什么角度去考虑的?
(3)我们是通过什么方法得出平行四边形的这几种判定方法的?
(4)本节课在探索平行四边形的判定方法时渗透了哪些数学思想方法?“猜想” -----“动手实践” -----“验证猜想(证明)”-----“得出结论”平行四边形三角形7.知识小结转化连接对角线1.必做作业:完成同步练习《18.2.1》
2.选做作业:自主探究平行四边形的其他判定方法。
课后作业8.作业布置谢谢您的倾听
形的性质:对角相等邻角互补对角线
互相平分BACO∵四边形ABCD
是平行边形 ∴OA=OC,OB=OD中心对称图形D对边平行对边相等∵四边形ABCD
是平行四边形 定义:两组对边分别平行的四边形是平行四边形。∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= 180°,∠A+∠D=180°∵四边形ABCD
是平行边形 1.复习回顾两组对边分别平行 平行四边形性质判定定义既是性质,也是判定方法.几何语言:平行四边形的判定1(定义法)定义:两组对边分别平行的四边形是平行四边形。∵ AD∥BC,AB∥DC
∴ 四边形ABCD是平行四边形 如图所示,某小区内修了两条相交公路,记为线段AB和线段BC.小区物业要以两条路为邻边修建一个平行四边形绿化带,请你帮物业想一想,如何确定平行四边形另外两边?2.情景引入命题1:两组对边分别相等的四边形是平行四边形。已知:四边形ABCD中,AB=CD,AD=BC
求证:四边形ABCD是平行四边形BDAC命题2:一组对边平行且相等的四边形是平行四边形。已知:如图,在四边形ABCD中,AB//CD,AB=CD
求证:四边形ABCD是平行四边形 BCDA已知:四边形ABCD中,AB=CD,AD=BC
求证:四边形ABCD是平行四边形∵ AB=CD,AD=BC
又∵ AC=AC
∴△ABC≌△CDA(S.S.S)
证明:连接AC,命题1:两组对边分别相等的四边形是平行四边形。∴∠1=∠2,∠3=∠4
∴ AB∥CD,AD∥BC
∴四边形ABCD是平行四边形真命题(两组对边分别平行的四边形是平行四边形)已知:如图,在四边形ABCD中,AB//CD,AB=CD,
求证:四边形ABCD是平行四边形. 证明:如图,连接 AC
∵AB //CD ,∴∠1=∠2.
又 ∵AB =CD , AC =CA ,
∴△ABC≌△CDA.
∴∠BCA=∠DAC .
∴ AD // BC .
∴四边形ABCD是平行四边形.命题2:一组对边平行且相等的四边形是平行四边形(两组对边分别平行的四边形是平行四边形)已知:四边形ABCD中,AB=CD,AD=BC
求证:四边形ABCD是平行四边形BDAC命题1:两组对边分别相等的四边形是平行四边形。 四边形ABCD是平行四边形AB∥ CD,AD ∥ BC△ABC≌△CDA∠1=∠2, ∠3=∠4(S.S.S)平行四边形三角形(证明角相等)思路:定义法转
化连
接
对
角
线 两组对边分别相等的四边形是平行四边形。判定定理1∵ AD=CB,AB=DC,
∴ 四边形ABCD是平行四边形 几何语言:3.归纳定理一组对边平行且相等的四边形是平行四边形判定定理2∴四边形ABCD是平行四边形.几何语言:强调:同一组对边平行且相等.AB∥CD且AB=CD,记作“AB CD”读作:“AB平行且等于CD”在四边形ABCD中,
∵AB//CD,AB =CD, 一组对边平行,另一组对边相等的四边形是平行四边形吗?假命题3.归纳定理4.知识梳理1.如图,在四边形ABCD中,AD=BC,要使四边形ABCD为平行四边形,可以添加的条件是 _______.(添加一个即可)
2.在四边形ABCD中,BD是对角线,下列条件中,不能判断四边形ABCD是平行四边形的是( )A.AB=CD, AD=BC
B.AB∥CD,∠1=∠2
C.AD=BC, ∠1=∠2
D.AB=CD, ∠1=∠2AD∥BC(或AB=CD)5.小试牛刀D试试看,哪位同学答得又快又准!例.如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AF=CE.
求证:四边形AECF是平行四边形. 证明:∵四边形ABCD是平行四边形
∴AD∥ CB(平行四边形的对边平行)
即:AF∥ CE
又∵ AF=CE
∴ AECF是平行四边形(一组对边平行且相等的四边形是平行四边形)思考:你还有别的方法吗?6.例题精析(1)本节课学习了哪几种判定平行四边形的方法?
(2)这些方法是从什么角度去考虑的?
(3)我们是通过什么方法得出平行四边形的这几种判定方法的?
(4)本节课在探索平行四边形的判定方法时渗透了哪些数学思想方法?“猜想” -----“动手实践” -----“验证猜想(证明)”-----“得出结论”平行四边形三角形7.知识小结转化连接对角线1.必做作业:完成同步练习《18.2.1》
2.选做作业:自主探究平行四边形的其他判定方法。
课后作业8.作业布置谢谢您的倾听
