实数
图片预览

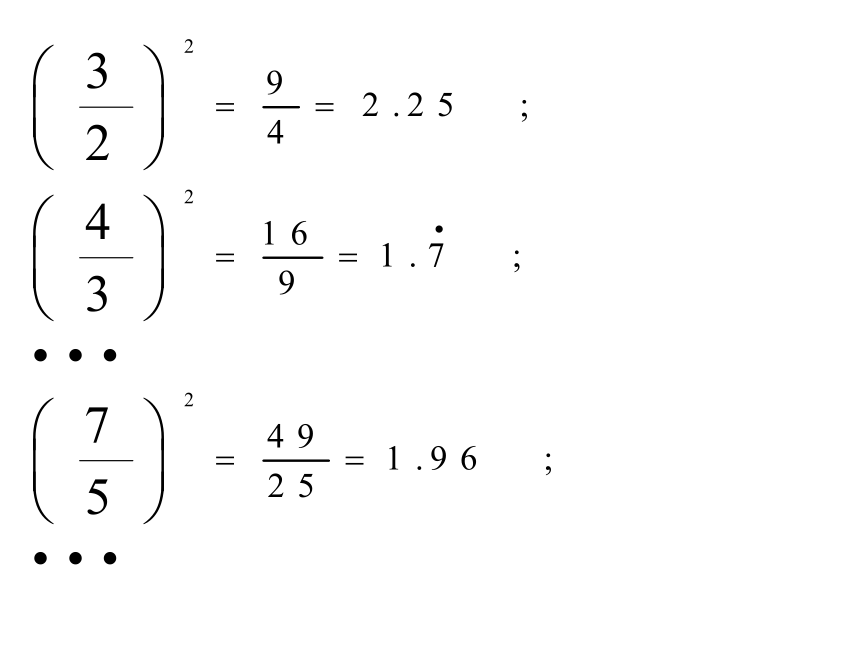





文档简介
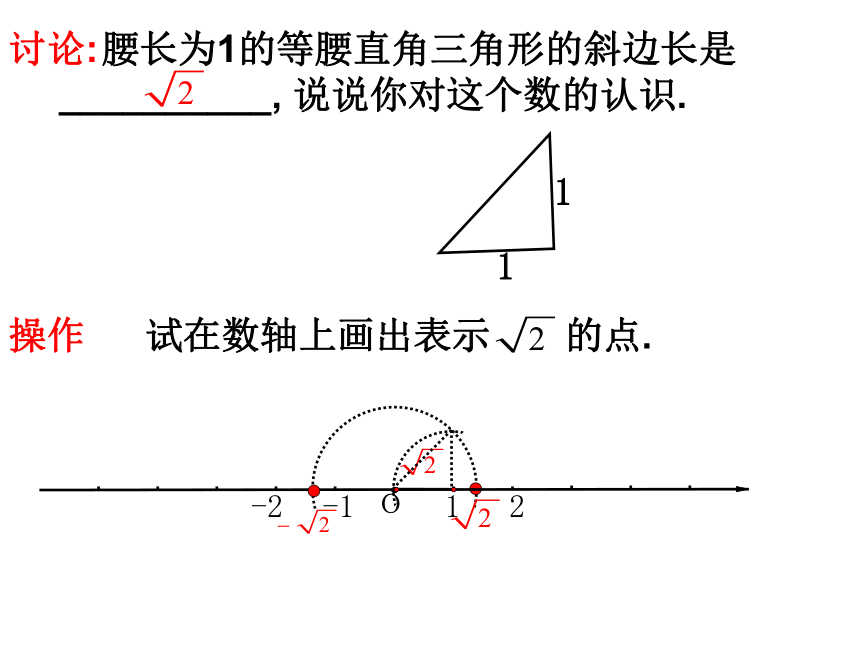
课件22张PPT。 腰长为1的等腰直角三角形的斜边长是__________, 说说你对这个数的认识.讨论:操作试在数轴上画出表示 的点.11因为 哪些分数的平方与2接近呢?讨论 (1) 是一个整数吗? (2) 是一个分数吗? 因为所以结论数学思想:无限逼近的数学思想1.无理数的概念无限不循环小数称为无理数.两个条件:①无限小数;②不循环小数
缺一不可2.5实数(1)2.实数的概念: 有理数和无理数统称为实数.
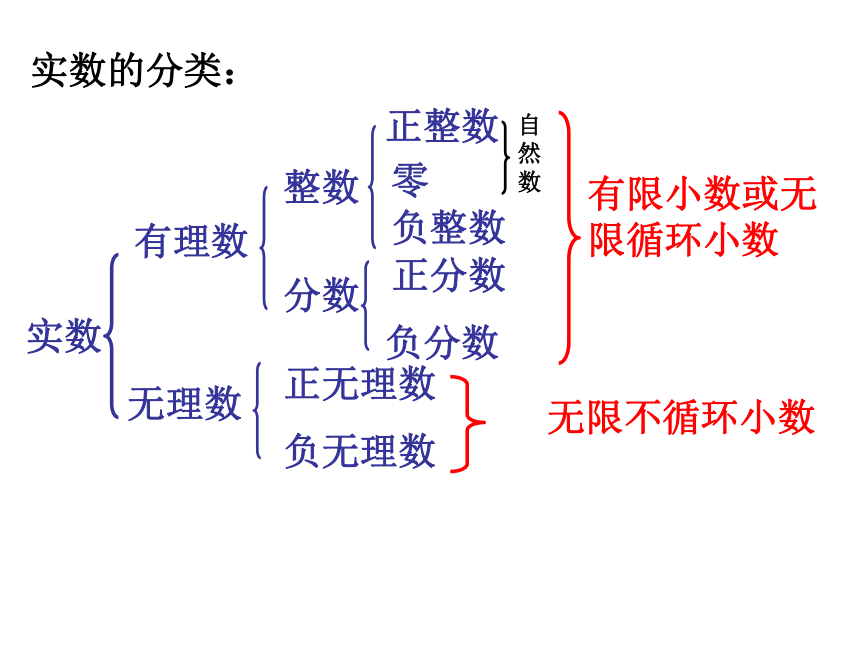
即实数可分为有理数和无理数. 到目前为止,同学们知道的数有哪些?你能给它们分类吗?讨论实数有理数无理数整数零分数正无理数负无理数正整数负整数正分数负分数有限小数或无限循环小数无限不循环小数实数的分类:自然数实数正实数负实数正有理数零负有理数正无理数负无理数还可如下分类(4)负实数集合{ …} (3)正实数集合{ …} 例题把下列各数填人相应的集合内:练习1:判断:(1)无理数都是无限小数 ( )(2)无限小数都是无理数 ( )(3)两个无理数的和一定是无理 ( )( )( )(6)整数和分数统称为有理数 ( )√××××√2.把下列各数分别填入相应的集合中:整数集合分数集合有理数集合无理数集合············讨论 有理数都可以用数轴上的点来表示, 反过 来,数轴上的点是否都表示有理数? 每一个实数都可以用数轴上的一个点来表示,;反之,数轴上的每一个点都表示一个实数,实数与数轴上的点是一一对应的。1.和数轴上的点一一对应的数集是 ( )
A. 有理数集 B. 无理数集 C. 整数集 D. 实数集
2.在实数
中整数有_______________________________;
有理数有______________________________;
无理数有_____________________________. D3.下列语句中正确的是 ( ) A.带根号的数都是无理数 B.不带根号的数都是有理数 C.无理数一定是无限不循环小数 D.无限小数一定是无理数C4.(1)在数轴上找出表示 的点.(2)在数轴上找出表示 的点.8. 无理数与有理数的积是无理数. ( )1. 无限小数是无理数. ( )下列说法正确与否, 若错则举例说明:想一想 × 2. 无理数是无限小数. ( )√ 3. 无理数就是开不尽根的数. ( )× 4. 带根号的数都是无理数. ( )× 5. 无理数与无理数的和是无理数. ( )6. 无理数与有理数的和是无理数. ( )7. 无理数与无理数的积是无理数. ( )× × × √ 9. 任何无理数的绝对值总是正数. ( )√ 这节课,我的收获是---无理数的常见形式:
①π是无理数;
② 带根号且开方开不尽的数;
③0.1010010 001…通过“逼近”的数学思想,体会到无理数的存在实数与数轴上的点是一一对应的初次体会到“数形结合”的数学思想实数有理数无理数整数零分数正无理数负无理数正整数负整数正分数负分数有限小数或无限循环小数无限不循环小数实数的分类:自然数实数正实数负实数正有理数零负有理数正无理数负无理数还可如下分类会将一个数进行分类是重点能将一个无理数在数轴上表示出来是难点
缺一不可2.5实数(1)2.实数的概念: 有理数和无理数统称为实数.
即实数可分为有理数和无理数. 到目前为止,同学们知道的数有哪些?你能给它们分类吗?讨论实数有理数无理数整数零分数正无理数负无理数正整数负整数正分数负分数有限小数或无限循环小数无限不循环小数实数的分类:自然数实数正实数负实数正有理数零负有理数正无理数负无理数还可如下分类(4)负实数集合{ …} (3)正实数集合{ …} 例题把下列各数填人相应的集合内:练习1:判断:(1)无理数都是无限小数 ( )(2)无限小数都是无理数 ( )(3)两个无理数的和一定是无理 ( )( )( )(6)整数和分数统称为有理数 ( )√××××√2.把下列各数分别填入相应的集合中:整数集合分数集合有理数集合无理数集合············讨论 有理数都可以用数轴上的点来表示, 反过 来,数轴上的点是否都表示有理数? 每一个实数都可以用数轴上的一个点来表示,;反之,数轴上的每一个点都表示一个实数,实数与数轴上的点是一一对应的。1.和数轴上的点一一对应的数集是 ( )
A. 有理数集 B. 无理数集 C. 整数集 D. 实数集
2.在实数
中整数有_______________________________;
有理数有______________________________;
无理数有_____________________________. D3.下列语句中正确的是 ( ) A.带根号的数都是无理数 B.不带根号的数都是有理数 C.无理数一定是无限不循环小数 D.无限小数一定是无理数C4.(1)在数轴上找出表示 的点.(2)在数轴上找出表示 的点.8. 无理数与有理数的积是无理数. ( )1. 无限小数是无理数. ( )下列说法正确与否, 若错则举例说明:想一想 × 2. 无理数是无限小数. ( )√ 3. 无理数就是开不尽根的数. ( )× 4. 带根号的数都是无理数. ( )× 5. 无理数与无理数的和是无理数. ( )6. 无理数与有理数的和是无理数. ( )7. 无理数与无理数的积是无理数. ( )× × × √ 9. 任何无理数的绝对值总是正数. ( )√ 这节课,我的收获是---无理数的常见形式:
①π是无理数;
② 带根号且开方开不尽的数;
③0.1010010 001…通过“逼近”的数学思想,体会到无理数的存在实数与数轴上的点是一一对应的初次体会到“数形结合”的数学思想实数有理数无理数整数零分数正无理数负无理数正整数负整数正分数负分数有限小数或无限循环小数无限不循环小数实数的分类:自然数实数正实数负实数正有理数零负有理数正无理数负无理数还可如下分类会将一个数进行分类是重点能将一个无理数在数轴上表示出来是难点
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
